В настоящий момент проблеме обработки информации в экономике придается весьма большое значение, поскольку обработка представляет собой начальную стадию анализа. Обработка информации независимо от природы ее получения представляет собой целый комплекс специальных процедур с целью получения определенного результата [1].
Одной из особенностей информации является ее стохастическая природа [2]. Данное обстоятельство открывает широкие границы взаимодействия методов экономического анализа в совокупности с теорией вероятности и математической статистикой. Широко известно, что для полноценной характеристики вероятностных данных необходимо и достаточно знание закона, которому эти данные подчиняются [3].
Однако на практике достаточно распространена ситуация, когда исследователь подобным знанием не обладает, а использует лишь некий массив данных, ничего не зная о природе его распределения [4]. Данные ситуации проявляются достаточно часто в системах, обладающих свойством динамичности или же неопределенности [5, 6]. При этом необходимо отметить, что идентификация закона распределения – достаточно сложная задача, решение которой, учитывая некорректность даже самой постановки, является априори несостоятельным [7]. Потому на практике исследователь, как правило, принимает неизвестный ему массив как нормально распределенный, что в итоге может исказить получаемые результаты [8].
Во избежание подобных искажений имеется необходимость если не идентифицировать, то хотя бы сделать обоснованное предположения о характере распределения, основываясь на самих данных в исследуемом массиве [9]. Известно также, что ключевую роль в идентификации закона распределения играет количество данных, которым располагает исследователь для анализа [10]. Также определено, что количество данных в значительной степени оказывает влияние на результат любого эксперимента, в том числе и идентификацию закона распределения [11, 12]. Отсюда возникает вопрос степени влияния на итоговый результат [13].
Стоит отметить, что, несмотря на широкие исследования в данной области, на настоящий момент не существует строгих универсальных рекомендаций, касающихся необходимого и достаточного количества данных для получения достоверного результата исследования [14]. Существующие на сегодня рекомендации относительно объема распределения носят только достаточно общий характер или же касаются лишь определенных ограниченных критериев [15, 16].
Цель исследования: определить влияние размера выборки на ключевые параметры определенных законов распределения.
Задачи исследования:
– провести анализ литературных источников, посвященных восстановлению закона распределения, с упоминанием количеств данных в выборке;
– исследовать выборки различного объема, подчиняющиеся различным распределениям, на предмет отклонения основных параметров распределения выборки от параметров генеральной совокупности;
– определить наиболее подходящие функции регрессии для различных законов распределения.
Материалы и методы исследования
Исследования проведены на базе кафедры управления и информатики в технических системах Оренбургского государственного университета. Для получения необходимых массивов данных использовался генератор случайных чисел программы Mathcad 15. Часть данных была обработана посредством пакета прикладных программ MS Excel. Данный пакет использовался также для хранения исходных данных и полученных в ходе исследования результатов. Проводился анализ трудов как отечественных, так и зарубежных авторов. Предпочтение отдавалось как наиболее известным авторам, так и последним данным, посвященным анализу данного вопроса.
Литературные источники изучались на предмет рекомендаций количества значений массива для применимости того или иного метода, связанного с идентификацией закона распределения. В ряде работ [17, 18] упоминается применение критерия проверки нормальности распределения Шапиро–Уилка при количестве данных не менее 7. В других работах количество еще выше [19, 20]. В работе [21] указано, что количество значений в массиве при использовании процедуры определения закона распределения (в частности, при проверке нормальности) должно составлять не менее 7. В некоторых других работах [22, 23] также есть ссылка на то, что минимальный размер данных должен быть не ниже 7 исследований в выборке.
Таким образом, определен минимальный уровень количества значений. Работ, в которых бы рассматривалось менее 7 значений для идентификации, в процессе анализа не выявлено. В рамках проведенного литературного обзора рассмотрено более 20 литературных источников.
Однако литературный анализ не является показателем при постановке эксперимента [24]. Необходимо определить, насколько изменяется точность исследования при изменении количества данных. Для этих целей были сгенерированы массивы размером в 10000 данных для различных распределений. В качестве законов распределения рассмотрим наиболее распространенные из них: нормальный, экспоненциальный, равномерный, логнормальный, логистический, биноминальный, геометрический, гипергеометрический, распределения Рэлея, Коши, Пуассона.
Из массивов вновь при помощи генератора случайных чисел были взяты подвыборки различного объема. Объем подвыборок определялся исходя из общих рекомендаций, взятых из анализа литературных источников.
Для полученных подвыборок определялись основные характеристики распределений (среднее, стандартное отклонение и дисперсия для нормального, минимальное и максимальное значения, медиана для равномерного, интенсивность для экспоненциального распределения и т.д.), которые затем подвергались преобразованию для дальнейшей обработки по следующей формуле:
Δ = |Pg – Ps|. (1)
где Pg – параметр генеральной совокупности, Ps – параметр выборки.
Результаты исследования и их обсуждение
Объединяя данные, полученные из всех исследуемых литературных источников, необходимо составить общее представление о том количестве значений, которым оперируют исследователи в процессе проведения своих работ. Для этого составим рейтинг количества значений в исследуемых выборках, которые используются при постановке эксперимента и получении экспериментальных результатов (рис. 1).
Как показывают данные рисунка, наиболее популярными в исследованиях являются числа 10, 100 и 1000.
В результате определено, что совокупный размер отклонений конкретного параметра выборки от параметра генеральной совокупности заметно снижается в зависимости от размеров выборки, причем на данную выявленную тенденцию существенного влияния не оказывает ни вид закона распределения, ни конкретный параметр, а только размер совокупности изучаемых данных.
Для полученных рядов данных подбирались модели регрессии. Однако ни одна из распространенных функций (логарифмическая, экспоненциальная, линейная, степенная, полиномиальная) не давала значимой величины аппроксимации (максимальная – у логарифмической функции, равная 0,056).
Исходя из данного обстоятельства, исследуемые массивы были разбиты на участки. После перебора нескольких вариантов наиболее оптимальными оказались следующие интервалы: 7–100, 100–1000, 1000–10000. В качестве примера отобразим отклонение среднего значения нормального распределения (рис. 2–4).
Проведенный регрессионный анализ методом наименьших квадратов показал, что в абсолютном большинстве случаев независимо от вида параметра и закона распределения наибольшей величиной достоверности аппроксимации обладает линейная функция. Все остальные аппроксимирующие уравнения имеют весьма низкую точность и уровень достоверности. При этом коэффициенты линейной функции на интервале от 1000 до 10000 данных весьма незначительны, что говорит о слабом изменении параметра при исследовании свыше 1000 значений.
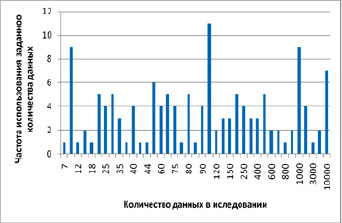
Рис. 1. Рейтинг количества значений, используемых в различных исследованиях
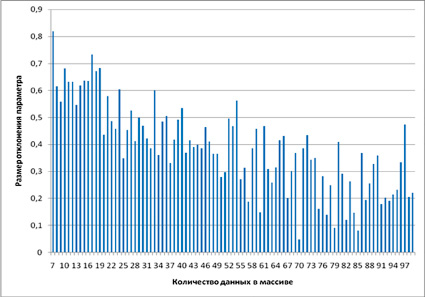
Рис. 2. Размер отклонений выборочного среднего от среднего значения генеральной совокупности на интервале 7–100
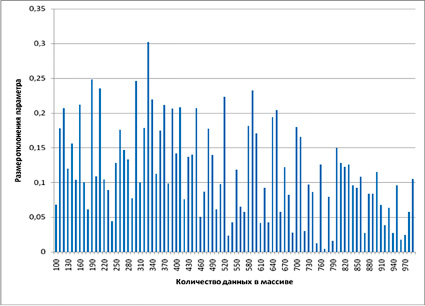
Рис. 3. Размер отклонений выборочного среднего от среднего значения генеральной совокупности на интервале 100–1000
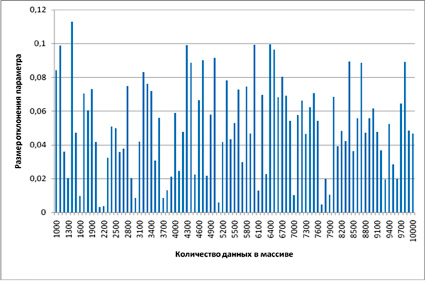
Рис. 4. Размер отклонений выборочного среднего от среднего значения генеральной совокупности на интервале 1000–10000
Заключение
В работе описано влияние количество данных в выборке при определении ключевых параметров закона распределения. Проведен анализ литературных источников, выявлено, что чаще всего исследователи берут 10, 100 и 1000 значений для проведения эксперимента.
Исследованы выборки различного объема на разных законах распределения, установлено, что с увеличением объема выборки величина отклонений достаточно существенно убывает.
Проведен регрессионный анализ, определено, что наиболее подходящим способом описания изменения данных в зависимости от количества является разбиение общего интервала на участки до 100 значений, 100–1000 значений, свыше 1000 значений, которые затем аппроксимируются линейной функцией, независимо от исследуемого параметра и закона распределения, которому подчиняется исследуемый массив.
Библиографическая ссылка
Акимов С.С., Трипкош В.А. ИССЛЕДОВАНИЕ ВЛИЯНИЯ ОБЪЕМА МАССИВА ДАННЫХ НА КЛЮЧЕВЫЕ ВЫБОРОЧНЫЕ ПАРАМЕТРЫ РАЗЛИЧНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ // Современные наукоемкие технологии. 2023. № 11. С. 10-15;URL: https://top-technologies.ru/ru/article/view?id=39813 (дата обращения: 07.03.2026).
DOI: https://doi.org/10.17513/snt.39813



