Актуальность задачи оперативного контроля стабильности технологического процесса основывается на высоких издержках, возникающих при массовых отзывах продукции, которые исчисляются миллионами рублей.
Анализ стабильности технологического процесса можно реализовать при помощи программно-аппаратного комплекса, который включает в себя программное обеспечение класса MES, систему сбора данных, алгоритмы и методы выявления сбоев внутри производства.
Применение цифровых технологий Индустрии 4.0 [1] «цифрового двойника» позволяет обеспечить необходимый уровень достоверности и актуальности данных внутри осуществляемой производственной деятельности. Пример реализации такого комплекса подробно описан в публикации [2] и реализован на предприятии ОНПП «Технология» им. А.Г. Ромашина.
Методика, описанная в [3], позволяет анализировать данные технического процесса, обрабатывать их, делать выводы о качестве производства, но обладает рядом недостатков внутри математического аппарата, выбранный метод статистического анализа не дает полного анализа.
Целью исследования является усовершенствование методики на основе статистических методов и критериев, по которой можно будет анализировать стабильность производства, делать вывод о состоянии технологического процесса и устранить недостатки ранее описанной работы.
Оценка качества производства с помощью статистических методов начинается с сформирования выборки данных. В случае технологического процесса модель составляется через бинарные величины, т.е. предполагается, что результаты контроля фиксированного количества изделий можно рассматривать как совокупность независимых одинаково распределенных случайных величин, которые принимают значение 0, если изделие дефектно, и 1, если дефекты не были обнаружены и изделия являются годными.
Эффективная методика должна содержать вопрос о распределении полученной выборки.
Из Центральной предельной теоремы следует, что при увеличении объема выборки распределение случайной величины сближается с нормальным распределением. Увеличение объема выборки, с другой стороны, приводит к увеличению времени анализа и росту затрат на обнаружение нестабильности ТП, таким образом, допускать, что выборка распределена по нормальному закону, некорректно.
Для правильного выбора методики следует выбрать критерий, по которому можно опровергнуть или принять статистическую гипотезу о распределении.
Критерий Пирсона является наиболее часто используемым критерием проверки статистических гипотез в научных работах по причине его точности и достоверности результатов. Преимущества и сравнение критерия Пирсона с другими существующими критериями подробно рассмотрены в работе [4].
В этом исследовании предлагается методика анализа стабильности производства с помощью критерия Пирсона, выводы о распределении выборки брака на производстве и о возможности применения данного критерия как показателя ухудшения или улучшения технологического процесса.
Выборка строилась на данных 2020–2022 гг., взятых с крупного предприятия керамической продукции, где дефекты у изделия приводят к полному разрушению. В предыдущих исследованиях была доказана возможность моделирования выборки внутри такого типа производства с помощью биномиального закона. Таким образом, следует проверить статистическим критерием именно эту гипотезу о моделировании выборки на производствах с разрушающим контролем и посмотреть реагирование критерия на изменение стабильности технологического процесса. Данное допущение о распределении выборки предполагается во многих научных работах последних лет.
Точность и достоверность результатов критерия Пирсона были проверены на случайно сгенерированных выборках. Результаты исследования и срабатывания методики по данным ОНПП «Технология» им. А.Г. Ромашина были подтверждены данными о технологическом процессе у технологов предприятия.
Материалы и методы исследования
Статистический контроль технологического процесса – одно из важных условий как рентабельного управления качеством выпускаемой продукции, так и способа повышения стабильности и эффективности производства.
Изучению данного вопроса уделяется много времени и внимания, опубликовано множество научных исследований по данной тематике. Так, в работе [5] рассмотрены различные виды и инструменты статистического контроля, программное обеспечение, содержащие методы многомерного статистического анализа, статистических случайных процессов и временных рядов, а также методы статистического регулирования технологического процесса. Основными методами в исследовании систематического контроля качества были выделены: контрольная карта, контрольный лист, стратификация, гистограмма, анализ Паретто, причинно-следственная диаграмма Исикавы и диаграмма разброса.
Контрольные карты как статистический метод были подробно рассмотрены в исследовании В.И. Кузнецова [6]. Различают качественные и количественные контрольные карты в зависимости от типа показателя качества. Применение контрольных карт позволяет предугадать появление дефектных изделий и помогает предположить изменение технологического процесса. В анализе технологического процесса внутри производства широко используются статистические критерии.
Во многих исследованиях используют метод анализа данных – «правило трех сигм» [7]. Правило трех сигм показывает, что вероятность того, что случайная величина (ошибка) отклонится от указанного диапазона, пренебрежимо мала, а значения, которые лежат вне полученного интервала, являются нарушением и отклонением технического процесса.
В исследовании, проведенном на базе предприятия ОНПП «Технология» им. А.Г. Ромашина, было рассмотрено и использовано правило трех сигм для значения атрибутивной величины – коэффициента запуска. Результаты, полученные таким способом, являются не совсем верными, так как использование правила трех сигм предполагает нормальное распределение величины, что в случае величины коэффициента запуска является неверным предположением. Коэффициент запуска по определению – это отношение числа изделий, запущенных в производство, к числу годных изделий.
В работе [8] были построены контрольные карты методом, схожим с правилом трех сигм. Отличие метода заключается в том, что вероятность отказов в сформулированной модели для качественных или количественных признаков, таких же, как коэффициент запуска, подчинена биномиальному закону.
Для выбора распределения следует рассмотреть понятие брака и дефектов в процессе производства. Изучение бракованных изделий, причин брака и видов дефекта важно в управлении производством, данная тема до сих пор является актуальной. В одном из последних исследований по данному вопросу при составлении математической модели данные о дефекте были представлены в виде бинарной величины, так как брак может быть либо выявлен, либо пропущен [9]. С двоичными данными расчет модели как Гауссовское (нормальное) распределение создаст неточные и ненадежные оценки параметров. Автором В.Ю. Чертищевым был предложен алгоритм для оценки вероятности обнаружения дефекта, где статистическая модель основана на биномиальном распределении, за счет того, что вероятность обнаружения дефекта можно принять за отношение совокупности дефектов, которые будут найдены при многократном осмотре.
В работе [10] при бинарных значениях данных в условиях малых выборок поведение случайных величин определяют также биномиальным законом распределения. Такое допущение было выбрано потому, что применять разработанный алгоритм при большом количестве опытов, который позволит использовать методы описательной статистики, основанной на нормальном распределении случайных величин, экономически невыгодно производствам.
Разница в моделировании бракованных изделий при разных законах распределения хорошо описана в исследовании [11], где моделирование потока случайных событий появления бракованных деталей выполнялось в MathCad, но с изначальным заданным нормальным распределением и вероятностью появления брака, а не на основе данных c производства. Анализировались выборки объемом от 1000 до 100000 с шагом 50. Данные, сгенерированные таким образом, проверялись критерием Пирсона, который показывал, к какому распределению относится выборка. Результатом исследования стало то, что при любом объеме выборки в диапазоне от 200 до 10000 случайно сгенерированная величина бракованных изделий распределена биномиально. Изучение брака и дефектов на производстве является до сих пор открытой темой для изучения, и нет определенного правила рассмотрения бракованных изделий в производстве.
В данной работе предлагается улучшенный алгоритм, который является продолжением описанных выше работ.
Алгоритм статистического анализа
Критерий Пирсона, или критерий χ2 (Хи-квадрат), применяется для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению при достаточном объеме выборки. Критерий применим для любых видов функций, даже при неизвестных параметрах, что имеет место при анализе результатов механических испытаний, в этом заключается его уникальность. Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) для каждого из интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины. Число интервалов зависит от объема выборки. Для проверки критерия вводится статистика:
= 
, (*)
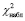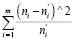где ni – частота события в интервале,
n'i – теоретическая частота события в интервале,
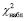– наблюдаемая величина критерия.
Рассчитанная наблюдаемая величина (*) критерия сравнивается с критическим значением критерия Пирсона. Критическое значение (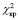
) является табличной величиной, зависящей от числа степеней свободы. Вывод по критерию Пирсона о принятии гипотезы делается по сравнению наблюдаемой величины критерия и критического значения. Гипотеза о распределении принимается и считается верной, если значение наблюдаемой величины меньше табличного критического значения (
< 
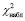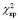), в противном случае гипотеза о распределении анализируемой выборки отвергается.
Для проверки результатов критерия Пирсона на точность и достоверность в программе RStudio были сгенерированы случайные выборки, распределенные по биномиальному закону с разными вероятностями (p): р = 0,5, р = 0,6, р = 0,7.
График (рис. 1) показывает значение наблюдаемой величины критерия (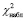
). На рисунке изображены четыре графика: значение наблюдаемой величины критерия у случайно сгенерированной биномиальной выборки с вероятностью, равной 0,5 (зеленый), значение наблюдаемой величины критерия у случайно сгенерированной биномиальной выборки с вероятностью, равной 0,6 (синий), значение наблюдаемой величины критерия у случайно сгенерированной биномиальной выборки с вероятностью, равной 0,7 (фиолетовый), и значение критической величины критерия (красный).
Из графика видно, что нет ни одного срабатывания критерия Пирсона (т.е. значения выше критического – красная прямая на графике) ни для одной из моделируемых биномиальных случайно сгенерированных выборок, значит, нет причин отвергнуть гипотезу об их распределении по биномиальному закону.
Для оценки выбранного метода был проведен анализ чувствительности данного критерия. Модель для оценки чувствительности критерия Пирсона была составлена из двух случайно сгенерированных выборок одинакового объема, распределенных по биномиальному закону, но с разными вероятностями. Данные две выборки были склеены последовательно в одну, и получившаяся выборка была протестирована в программе RStudio по критерию Пирсона, значения были усреднены на 100 реализаций программы и построен график срабатываний значений. Для анализа чувствительности были протестированы разные выборки одинакового объема, с разным шагом от 10 до 1000 и разными начальными вероятностями двух выборок, которые подлежали склеиванию.
Результатом программы были значения по критерию Пирсона и момент срабатывания для разных выбранных интервалов и разности вероятностей двух начальных выборок.
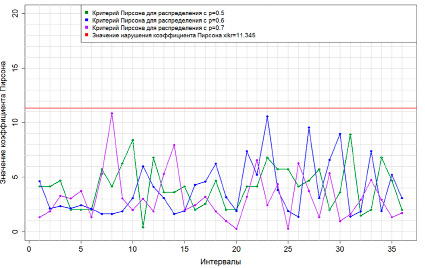
Рис. 1. График значений величины критерия для случайно сгенерированных биномиальных распределений с разными вероятностями
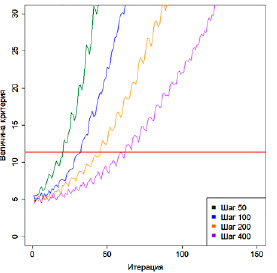
Рис. 2. График значений величины критерия для случайно сгенерированных биномиальных распределений с разным шагом
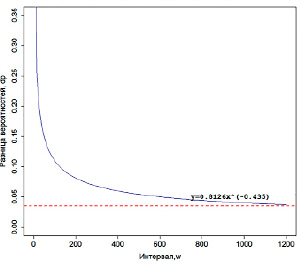
Рис. 3. График чувствительности критерия Пирсона
График (рис. 2) – пример работы программы при склейке двух случайных выборок объемом 500 и вероятностями, равными 0,5 и 0,7. На данном графике видно, что при определенной итерации критерий Пирсона срабатывает, и гипотеза о том, что выборка является биномиальным распределением, с начальной вероятностью 0,5 отвергается.
После множества тестирований и экспериментов с изменением начальных входных данных была выведена зависимость между разницей вероятностей выборок и интервалом анализа, минимально нужным для применения метода. Тренд данной зависимости показал, что она является степенной функцией с мерой совпадения 98,6 %. Это позволяет сделать вывод о том, что использование окна размером более 1200 изделий нецелесообразно, потому что критерий Пирсона не срабатывает при разнице вероятностей, которая равна или меньше 0,04.
Полученная зависимость разницы вероятностей и минимального интервала (рис. 3) для правильного реагирования метода без ложных срабатываний и есть чувствительность критерия Пирсона.
Результаты исследования и их обсуждение
Данный метод был применен на данных с предприятия ОНПП «Технология» им. А.Г. Ромашина. Были проанализированы данные 2020–2022 гг., взятые с базы данных ПО ПАУК, созданного в виде «цифрового двойника» предприятия. Сбор данных для анализа был организован в виде запроса в программе и выгружен для создания дальнейшей выборки. Анализ стабильности производства проводился по месяцам с помощью критерия Пирсона. Выводы относительно стабильности гипотезы делались от результатов критерия Пирсона. Срабатывание критерия, когда значение наблюдаемого критерия Хи-квадрат выше табличного критического значения, означает, что выборка не является биномиальным распределением с начальной вероятностью, и произошли некие изменения в процессе производства. При отсутствии срабатывания критерия значения ниже критического соответствуют тому, что производство стабильно.
Анализ стабильности включает в себя не только выводы по критерию Пирсона, но и вспомогательные величины. Величина, также характеризующая технологический процесс, коэффициент запуска. Коэффициент запуска – величина, показывающая отношение всех изделий, запущенных в производство, к числу годных изделий. Задача предприятия состоит в том, чтобы принимать меры по уменьшению коэффициента запуска для улучшения производства и своевременно обнаруживать повышение коэффициента запуска для устранения проблемы, возникшей внутри технологического процесса. На рис. 4 отображен график метода анализа стабильности, где сами точки (рис. 4 – черный цвет) графика – это значения наблюдаемой величины критерия Пирсона, а над ними посчитан коэффициент запуска.
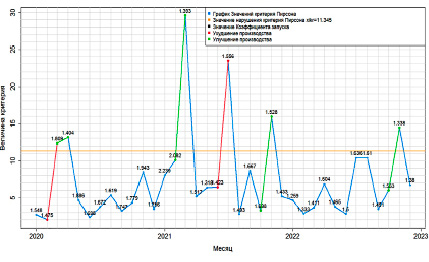
Рис. 4. График метода анализа стабильности по критерию Пирсона за 2020–2022 гг. по данным предприятия
Выводы об изменениях технологического процесса можно делать на основе совокупности двух расчетов. Отсутствие срабатываний критерия Пирсона – производство стабильно. Срабатывание критерия Пирсона говорит о том, что в технологическом процессе произошли изменения, с учетом значения коэффициента запуска, уменьшение которого обозначает улучшение в производстве (рис. 4 – красный цвет отрезков), а увеличение означает ухудшение (рис. 4 – зеленый цвет отрезков). Полученные данные были проверены технологами предприятия, выводы методики совпали с историческими событиями на производстве.
Заключение
Внедрение элементов статистического анализа имеет большое значение для крупных предприятий. Методика позволяет оперативно выявить изменения в процессе производства, быстро среагировать на проблему, что приводит к уменьшению времени на поиск и реализацию решения проблемы. На основании предыдущих исследований модель распределения бракованных изделий определяется распределенной по биномиальному закону. Методика была улучшена добавлением в нее критерия Пирсона, который позволяет сделать выводы о распределении выборки. Критерий Пирсона был проверен на точность и надежность на случайных моделях, также получена зависимость критерия, которая позволяет с нужной чувствительностью к разнице вероятностей подобрать минимальный интервал для исследования выборки. Отсутствие срабатывания критерия говорит о том, что производство стабильно. Расчет коэффициента запуска в совокупности с критерием Пирсона помогает увидеть, в какую сторону направлены изменения технологического процесса. Увеличение коэффициента запуска отражает негативные изменения, уменьшение – положительные.
Методика была опробована на данных крупного предприятия керамической продукции. Результаты методики подтверждены данными технологов предприятия, улучшения отражают время введения новых операций или замену материала на производство, ухудшения отражают отклонения внутри технологического процесса.
Результаты исследования и алгоритм статистического анализа могут быть использованы для внедрения в системы автоматизированного управления наукоемкими производствами. В дальнейшем методика может быть усовершенствована добавлением еще одного статистического критерия для анализа или более полным анализом минимального интервала выборки для необходимой чувствительности вероятности.
Библиографическая ссылка
Харитонов Д.В., Грошев А.В., Рамазанова А.А., Маслова Е.В. ПРИМЕНЕНИЕ КРИТЕРИЯ ПИРСОНА ДЛЯ ОЦЕНКИ СТАБИЛЬНОСТИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА // Современные наукоемкие технологии. – 2023. – № 9. – С. 61-67;URL: https://top-technologies.ru/ru/article/view?id=39761 (дата обращения: 21.11.2024).