Фундаментальные положения качественной теории дифференциальных уравнений изложены в [1, 2]. Современное состояние вопроса освещается в [3, 4], а также в [5–8]. При этом в работах, посвященных задачам устойчивости решений систем обыкновенных дифференциальных уравнений (ОДУ), основное внимание, как правило, обращено на метод функций Ляпунова и его содержание на современном этапе [3]. Предлагаются методы аналитического характера, вместе с тем представлены подходы к рассмотрению прикладных аспектов с применением средств вычислительной техники [4, 6], с преобразованиями функций правой части [7–9] и вычислением функции Ляпунова [10, 11]. Как правило, подходы к разработке прикладных методов не опираются на использование численных методов. Ниже предлагается решение прикладных задач анализа устойчивости именно на основе численных методов решения ОДУ. Ставится задача представить на этой основе необходимые и достаточные условия устойчивости в смысле Ляпунова решений ОДУ общего вида, указать границы применимости предлагаемых критериев, дать примеры численного эксперимента, иллюстрирующие излагаемый подход. При этом аналитические оценки устойчивости должны строиться непосредственно из компонентов правой части дифференциальной системы, без их вычислительных преобразований и без применения функции Ляпунова. Построение численных оценок устойчивости должно опираться на приближенное решение системы ОДУ и давать возможность анализа устойчивости по ходу компьютерной реализации численного интегрирования, что представляется актуальным для основных технических приложений.
Цель исследования заключается в том, чтобы найти необходимые и достаточные условия устойчивости решений систем ОДУ в границах существования и единственности решений. В аналитической форме критерии должны строиться непосредственно из компонентов правой части дифференциальной системы. В численной форме критерии должны опираться на приближенное решение системы и предоставлять возможность компьютерного анализа устойчивости по ходу решения в режиме реального времени. Требуется дать математическое обоснование искомых критериев, проиллюстрировать их достоверность с помощью численного эксперимента.
Исходные положения. Предполагается, что выполнено обычное преобразование задачи Коши для системы ОДУ, в результате которого анализ устойчивости решения в смысле Ляпунова (ниже устойчивости) сводится к анализу устойчивости нулевого решения 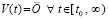 [1]. Преобразованная задача Коши с возмущенными начальными значениями ниже дана в виде
[1]. Преобразованная задача Коши с возмущенными начальными значениями ниже дана в виде
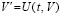 ,
, 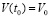 ,
, 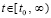 , (1)
, (1)
где
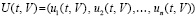 ,
,
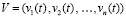 ,
,
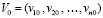 ,
, 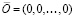 ,
,
все значения переменных предполагаются вещественными. Требуется исследовать устойчивость нулевого решения задачи (1). Возмущение (ненулевое решение) 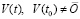 не будет отмечаться специальным символом и, как синоним, иногда будет называться просто решением задачи (1). Используются согласованные канонические нормы матрицы и вектора, по умолчанию
не будет отмечаться специальным символом и, как синоним, иногда будет называться просто решением задачи (1). Используются согласованные канонические нормы матрицы и вектора, по умолчанию 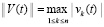 .
.
Предполагается, что 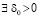 , такое, что в области
, такое, что в области
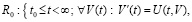
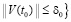
выполнены все условия существования и единственности решения задачи (1), при этом вектор-функция U(t,V) определена, непрерывна и непрерывно дифференцируема 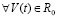 . Совокупность данных предположений в дальнейшем определяется термином «исходные предположения».
. Совокупность данных предположений в дальнейшем определяется термином «исходные предположения».
В исходных предположениях нулевое решение задачи (1) устойчиво, если 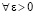 найдется
найдется 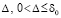 , такое, что
, такое, что 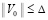 влечет
влечет 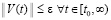 . Нулевое решение асимптотически устойчиво, если оно устойчиво и найдется
. Нулевое решение асимптотически устойчиво, если оно устойчиво и найдется 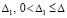 , такое, что из неравенства
, такое, что из неравенства 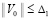 следует
следует 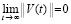 .
.
Необходимые и достаточные условия устойчивости нулевого решения на основе мультипликативного преобразования метода Эйлера. Для краткости компоненты решения vk(t) иногда обозначаются vk. Метод Эйлера приближенного решения задачи (1) по компонентам записывается в виде
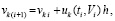
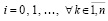 . (2)
. (2)
Шаг h предполагается равномерным, для произвольно выбранной независимой переменной 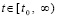 индекс i в (2) на отрезке [t0, t] неограниченно возрастает в соответствии убывающему на [t0, t] шагу –
индекс i в (2) на отрезке [t0, t] неограниченно возрастает в соответствии убывающему на [t0, t] шагу –
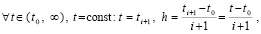
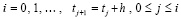 . (3)
. (3)
Для аналитических оценок метод Эйлера на каждом шаге рассматривается исключительно с остаточным членом, в этом случае на каждом шаге он может интерпретироваться как точный (без погрешности), именно,
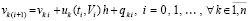 , (4)
, (4)
где qki – остаточный член формулы Тейлора в окрестности точки ti радиуса h для k-го компонента приближения:
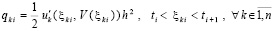 . (5)
. (5)
В обозначениях (4), (5) выполняются следующие преобразования:
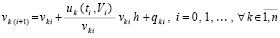 , (6)
, (6)
или,
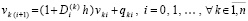 , (7)
, (7)
где
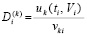 ,
,
qki из (5), метод Эйлера интерпретируется как два первых члена формулы Тейлора для k-го компонента решения. Пусть предполагается до тех пор, пока не оговорено иное, что
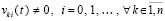 . (8)
. (8)
Кроме того, на время рассмотрения (7) (и только на это время) предполагается, что
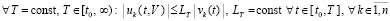 . (9)
. (9)
С учетом (9) при ограничении (8)
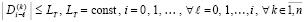 . (10)
. (10)
Предположения (8), (9) и (10) вводятся только на период рассмотрения (6), (7) с мультипликативными преобразованиями. В дальнейшем, начиная с применения аддитивных преобразований метода Эйлера, эти предположения, дополнительные к исходным предположениям, не будут считаться выполненными.
Точное значение компонентов решения задачи (1) преобразуется к виду
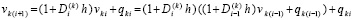 ,
,
или 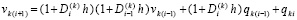 . Отсюда
. Отсюда
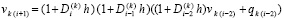 ,
,
так что
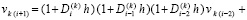
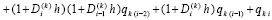 .
.
Далее, по рекуррентности,
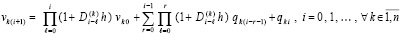 . (11)
. (11)
Пусть
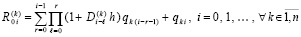 (12)
(12)
Лемма 1. В предположениях, дополнительно к исходным включающих (8), (9) и (10),
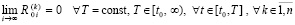 (13)
(13)
Доказательство [12, 13]. Для 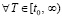
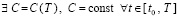 :
: 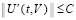 . Поэтому, согласно (5), (6), в (12)
. Поэтому, согласно (5), (6), в (12) 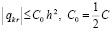 ,
, 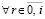 ;
; 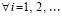 ,
, 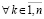 . Пусть
. Пусть 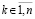 произвольно фиксировано. Очевидно,
произвольно фиксировано. Очевидно,
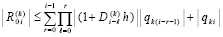 .
.
С учетом (10), 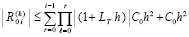 .
.
Отсюда 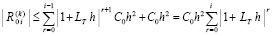 , что влечет
, что влечет
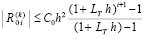 , или
, или
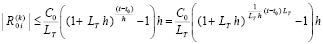 .
.
Уменьшаемое, монотонно возрастая, стремится к 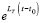 . Отсюда, с учетом (3),
. Отсюда, с учетом (3),
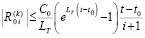 .
.
Таким образом, 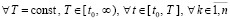 ,
, 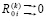 при i →∞. Лемма доказана.
при i →∞. Лемма доказана.
Следствие 1. В условиях леммы 1
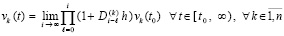 . (14)
. (14)
Доказательство. Предельный переход в (11) с учетом (12), (13) влечет (14).
Из леммы 1 и следствия 1 вытекает
Лемма 2 [12, 13]. В условиях леммы 1 для устойчивости нулевого решения задачи (1) необходимо и достаточно существование 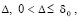 такого, что для всех решений
такого, что для всех решений 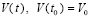 , при ограничении
, при ограничении 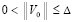 выполняется неравенство
выполняется неравенство
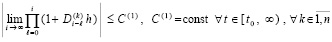 . (15)
. (15)
Для асимптотической устойчивости нулевого решения в тех же условиях необходимо и достаточно, чтобы выполнялось предыдущее утверждение и существовало 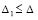 , такое, что неравенство
, такое, что неравенство 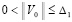 влечет
влечет
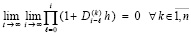 . (16)
. (16)
Соотношения леммы 2 упрощаются непосредственно ниже.
Условия устойчивости с обратной пропорцией начальным значениям. Из следствия 1 и (14)
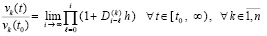 . (17)
. (17)
Согласно (17) из леммы 2 вытекает
Следствие 2 [13]. Условия, формулировка и утверждение леммы 2 дословно сохраняются при замене соотношения (15) на соотношение вида
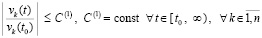 , (18)
, (18)
и (16) – на соотношение
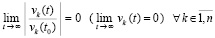 . (19)
. (19)
Таким образом, в основных предположениях, дополненных предположениями (8), (9) и (10), необходимое и достаточное условие устойчивости дает соотношение (18). Необходимое и достаточное условие асимптотической устойчивости дает одновременное выполнение (18) и (19), в (19) деление на vk(t0) можно исключить. Ограничения (8)–(10) существенно сужают область применения этих критериев. Однако, как будет показано непосредственно ниже, эти ограничения можно снять.
Необходимые и достаточные условия устойчивости на основе аддитивного преобразования метода Эйлера. Соотношение (14) представляет собой эквивалентное преобразование метода Эйлера с учетом остаточного члена. Аналогичное соотношение можно получить на основании аддитивного преобразования метода Эйлера, также с учетом остаточного члена. Именно, из (4)
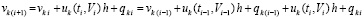 .
.
Отсюда
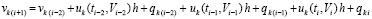 ,
,
и, далее, по рекуррентности,
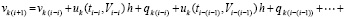
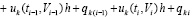 .
.
Окончательно
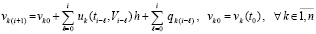 .
.
При i →∞ на любом отрезке [t0, t] получится
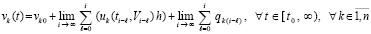 ,
,
где с учетом (3)–(5), в обозначениях доказательства леммы 1,
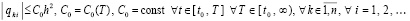 .
.
Предел суммы остаточных членов равен нулю. В самом деле, 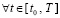 ,
,
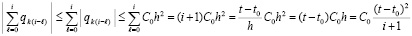 .
.
Отсюда 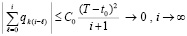 ,
,
следовательно, 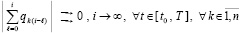 .
.
Вследствие того, что 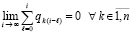 , с учетом произвольности выбора
, с учетом произвольности выбора 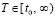 ,
,
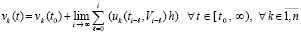 , (20)
, (20)
где h = h(i) из (3), h →0, i →∞, поэтому слагаемое под знаком суммы заключено в скобки. В каждой точке 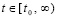 соотношение (20) представляет собой результат сходимости метода Эйлера на отрезке [t0, t].
соотношение (20) представляет собой результат сходимости метода Эйлера на отрезке [t0, t].
Замечание 1. Равенство (20) верно в более широких условиях, чем равенство (14). Оно непосредственно выводится из метода Эйлера с учетом остаточного члена без применения операций деления, что ранее требовало ограничения (8), и без использования неравенств (9) и (10). Для выполнения (20) достаточно изложенных вначале исходных предположений.
Как и в (14), в (20) можно выделить начальное значение в виде множителя:
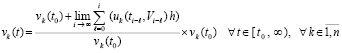 . (21)
. (21)
Из (21) очевидно, что устойчивость нулевого решения задачи (1) полностью определяется асимптотическим поведением дроби перед выделенным сомножителем vk(t0). Поскольку (21) эквивалентно (20), то с учетом замечания 1 соответственный критерий на основе данной дроби окажется применимым в условиях свободных от ограничений (8), (9) и (10). В результате лемма 2 переходит в следующую лемму.
Лемма 3. В исходных предположениях, не включающих ограничения (8), (9) и (10), для устойчивости нулевого решения задачи (1) необходимо и достаточно существование 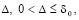 такого, что
такого, что 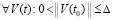 выполняется соотношение
выполняется соотношение
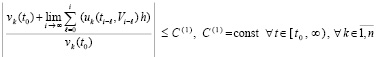 , (22)
, (22)
где h = h(i) из (3), h →0, i →∞. В тех же предположениях для асимптотической устойчивости нулевого решения необходимо и достаточно, чтобы выполнялось предыдущее утверждение и существовало 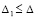 , такое, что неравенство
, такое, что неравенство 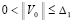 влечет
влечет
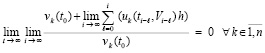 . (23)
. (23)
Соотношение (22) выполняется в предположениях существования и единственности решения задачи (1), а также дифференцируемости правой части (1) на полуоси. То же относится к (23). Согласно (21) в условиях леммы 3 во всей области R0 выполняется
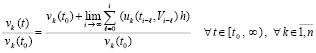 ,
,
где рассматриваются только возмущенные решения, так что заведомо 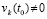 . Отсюда и из леммы 3 вытекает
. Отсюда и из леммы 3 вытекает
Теорема 1. В исходных предположениях, в которых, в частности, не требуется выполнения (8), (9) и (10), для устойчивости нулевого решения задачи (1) необходимо и достаточно существование 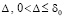 , такого, что
, такого, что 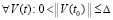 выполняется соотношение
выполняется соотношение
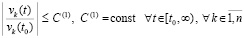 . (24)
. (24)
В тех же условиях для асимптотической устойчивости нулевого решения необходимо и достаточно, чтобы оно было устойчиво и существовало 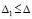 , такое, что
, такое, что 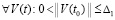 выполняется соотношение
выполняется соотношение
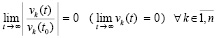 . (25)
. (25)
Таким образом, для критериев (24), (25) не требуется иных ограничений кроме существования и единственности решений, а также непрерывной дифференцируемости правой части (1) в R0. Неравенства (8), (10) были необходимы для обеспечения (13) и, соответственно, (14). Для выполнения (21) этого не требуется – достаточно исходных предположений.
Замечание 2. Ограничения (8)–(10) исключали целые классы уравнений из числа допускающих применение (24), (25). Так, если 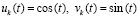 , то (8) нарушалось бы при всех
, то (8) нарушалось бы при всех 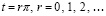
Поскольку в числителях соотношений (21)–(23) интеграл, приближенно вычисляемый по формуле прямоугольников, то с переходом к пределу при h →0 обосновывается
Следствие 3. Условия и утверждения теоремы 1 сохранятся, если соотношения (24) и (25) заменить соответственно на соотношение
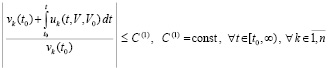 (26)
(26)
и
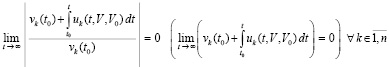 . (27)
. (27)
Очевидно, следствие 3 – разновидность теоремы 1. Вместе с тем (26), (27) дают возможность учитывать условия сходимости несобственного интеграла. Так, имеет место
Следствие 4. Если 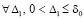 ,
, 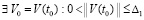 , такое, что
, такое, что 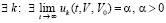 , то нулевое решение задачи (1) неустойчиво. Аналогично, в случае
, то нулевое решение задачи (1) неустойчиво. Аналогично, в случае 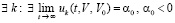 .
.
Доказательство. В условиях следствия 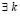 ,
, 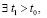

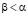 ,
, 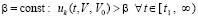 . Поэтому выполняется соотношение
. Поэтому выполняется соотношение
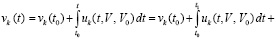
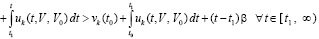 .
.
Отсюда vk(t) → ∞ при t → ∞, что исключает устойчивость нулевого решения.
Случай 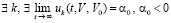 , рассматривается аналогично.
, рассматривается аналогично.
Следствие 5. Если 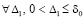 ,
, 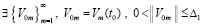 , такие, что выполняется соотношение
, такие, что выполняется соотношение
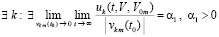 ,
,
то нулевое решение задачи (1) неустойчиво.
Аналогично, в случае 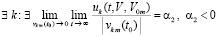 .
.
Доказательство. В условиях следствия 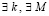 , такие, что
, такие, что 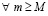 выполняется соотношение
выполняется соотношение 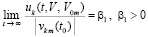 . Для таких k, M выполнены условия следствия 4, поэтому нулевое решение системы (1) неустойчиво.
. Для таких k, M выполнены условия следствия 4, поэтому нулевое решение системы (1) неустойчиво.
Случай 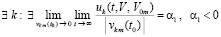 , рассматривается аналогично.
, рассматривается аналогично.
Согласно следствиям 4, 5 существование при некотором 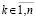 в любой произвольно малой окрестности нулевых начальных значений конечного и отличного от нуля предела
в любой произвольно малой окрестности нулевых начальных значений конечного и отличного от нуля предела 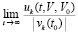 влечет неустойчивость нулевого решения. Отсюда имеет место
влечет неустойчивость нулевого решения. Отсюда имеет место
Следствие 6. Необходимым условием устойчивости нулевого решения задачи (1) является утверждение, что либо 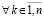 ,
,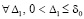 ,
, 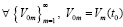 ,
, 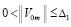
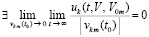 , (28)
, (28)
либо 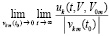 при некоторых
при некоторых 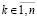 не существует, а для остальных k верно (28).
не существует, а для остальных k верно (28).
Замечание 3. Для устойчивости нулевого решения задачи (1) недостаточно стремления к нулю подынтегральной функции 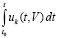 , недостаточно также выполнения соотношения
, недостаточно также выполнения соотношения 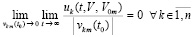 .
.
Необходимым и достаточным условием устойчивости является выполнение (26) в исходных предположениях, асимптотической устойчивости – одновременно (26) и (27). Аналогично, в исходных предположениях необходимые и достаточные условия устойчивости дает теорема 1.
В (26) vk(t0) тривиально вносится под знак интеграла. Значение vk(t0) может быть произвольно малым, от него зависит подынтегральная функция, в этой связи используется развернутое обозначение 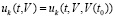 . Соотношение (26) эквивалентно
. Соотношение (26) эквивалентно
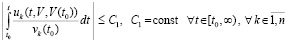 ,
,
(27) – 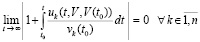 , что равносильно
, что равносильно
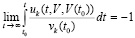 , или
, или 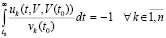 .
.
В результате следствие 3 перейдет в следующее утверждение.
Лемма 4. В исходных предположениях для устойчивости нулевого решения задачи (1) необходимо и достаточно существование 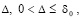 такого, что
такого, что 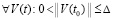 выполняется соотношение
выполняется соотношение
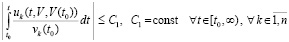 . (29)
. (29)
В тех же условиях для асимптотической устойчивости нулевого решения необходимо и достаточно, чтобы оно было устойчиво и существовало 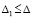 , такое, что
, такое, что 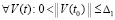 верно равенство
верно равенство
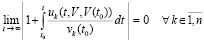 , (30)
, (30)
или, что равносильно,
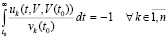 .
.
На основании леммы 4 для оценки устойчивости можно применить мажоранты. Так, (29) будет выполняться, если 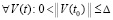 имеют место соотношения
имеют место соотношения
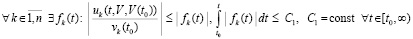 .
.
В частности, если 0 < t0 и 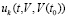 допускает выбор
допускает выбор 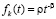 , где 1 < β, 0 < ρ, то
, где 1 < β, 0 < ρ, то
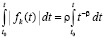 , тогда
, тогда 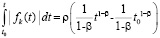 ,
,
где 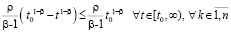 .
.
В этом случае будет выполняться (29):
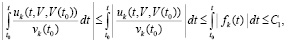
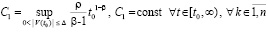 . (31)
. (31)
Если данный выбор ρ и β в 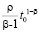 возможен в некоторой ∆-окрестности начальных значений, то (31) верно
возможен в некоторой ∆-окрестности начальных значений, то (31) верно 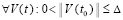 , и нулевое решение задачи (1) будет устойчиво в силу леммы 4. В этом же случае нулевое решение будет асимптотически устойчиво, если при условии
, и нулевое решение задачи (1) будет устойчиво в силу леммы 4. В этом же случае нулевое решение будет асимптотически устойчиво, если при условии 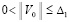 выполняются соотношения
выполняются соотношения
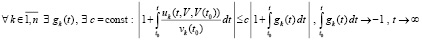 .
.
Так, если при значениях параметров из предыдущего примера функция 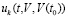 допускает выбор
допускает выбор 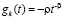 , то
, то
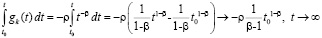 ,
,
и, при выборе 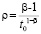 , будет выполнено
, будет выполнено 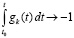 , следовательно, выполнится
, следовательно, выполнится
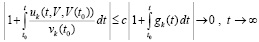 . (32)
. (32)
Если данный выбор ρ и β в 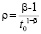 возможен в ∆1-окрестности начальных значений, то это будет означать, что (32) выполняется для всех решений V(t), при условии
возможен в ∆1-окрестности начальных значений, то это будет означать, что (32) выполняется для всех решений V(t), при условии 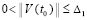 . Соответственно, в тех же условиях будет выполняться (30), что будет означать асимптотическую устойчивость нулевого решения задачи (1). Напротив, если
. Соответственно, в тех же условиях будет выполняться (30), что будет означать асимптотическую устойчивость нулевого решения задачи (1). Напротив, если 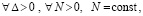
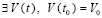 , такое, что при ограничении
, такое, что при ограничении 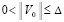 выполняется соотношение
выполняется соотношение
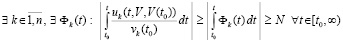 ,
,
то нулевое решение будет неустойчиво. Например, если данному неравенству в рассматриваемых условиях будет удовлетворять 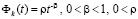 , то
, то
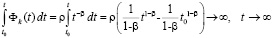 ,
,
что влечет неустойчивость нулевого решения.
В результате имеет место
Предложение 1. Пусть для задачи (1) выполнены исходные предположения. Если 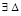 , такое, что
, такое, что 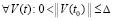 выполняется соотношение
выполняется соотношение
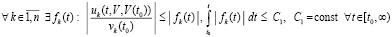 , (33)
, (33)
то нулевое решение задачи (1) устойчиво. В частности, это так, если в (33) можно выбрать 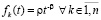 , где
, где 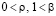 ,
,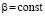 ,
,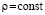 . Если нулевое решение устойчиво и при этом
. Если нулевое решение устойчиво и при этом 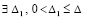 , такое, что неравенство
, такое, что неравенство 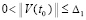 влечет выполнение соотношения
влечет выполнение соотношения
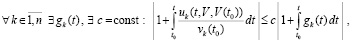
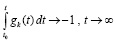 , (34)
, (34)
то нулевое решение асимптотически устойчиво. В частности, это так, если в (34) можно выбрать 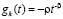 ,
,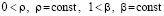 , при значении
, при значении 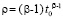 . Если
. Если 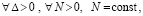
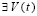 , такое, что при ограничении
, такое, что при ограничении 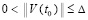 выполняется
выполняется
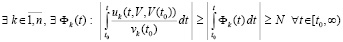 , (35)
, (35)
то нулевое решение неустойчиво. В частности, это так, если в (35) можно выбрать 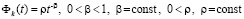 .
.
Непосредственно ниже в интегралах из (29), (30) рассматривается замена переменной 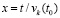 с обозначением
с обозначением 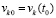 и
и 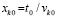 . Из
. Из 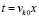 следует
следует 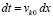 . Нижний предел интегрирования t0 переходит в xk0, верхний предел интегрирования t переходит в
. Нижний предел интегрирования t0 переходит в xk0, верхний предел интегрирования t переходит в 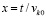 :
:
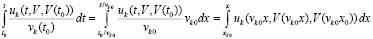 .
.
Окончательно
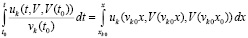 . (36)
. (36)
При использовании (36) лемма 4 перейдет в следующую лемму.
Лемма 5. В исходных предположениях для устойчивости нулевого решения задачи (1) необходимо и достаточно существование 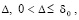 такого, что
такого, что 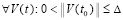 выполняется соотношение
выполняется соотношение
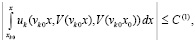
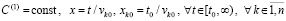 . (37)
. (37)
Для асимптотической устойчивости нулевого решения необходимо и достаточно, чтобы оно было устойчиво и существовало 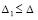 , такое, что
, такое, что 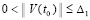 влечет
влечет
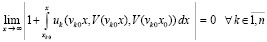 , (38)
, (38)
или,
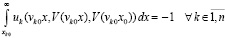 .
.
С той же заменой переменной следствие 3 примет следующий вид.
Следствие 7. В условиях и обозначениях леммы 5 утверждения этой леммы сохранятся, если (37) и (38) представить соответственно в разновидностях
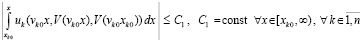 , (39)
, (39)
что равносильно
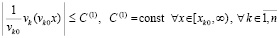 , (40)
, (40)
и
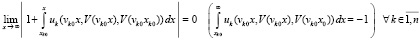 ,
,
что равносильно
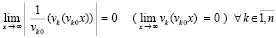 . (41)
. (41)
Доказательство. Из (26) и (36)
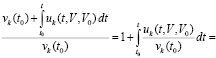
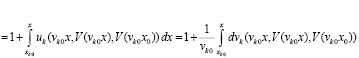 ,
,
где
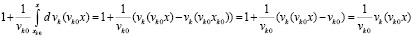 .
.
Отсюда следует (40), (41), эквивалентность (40) и (39), эквивалентность (41) и (38). Следствие доказано.
На основе (36)–(41) тривиально формулируется аналог предложения 1. Соотношения (38)–(41) могут применяться для аналитических оценок устойчивости с учетом обратной пропорции vk(t0).
Условия устойчивости с учетом знаков компонентов функции правой части и их производных. Для краткости компоненты uk(t, V) из (1) ниже обозначаются uk(t) и uk. Следующие утверждения указывают на роль обратной пропорции начальным значениям в представленных выше условиях устойчивости. Имеет место
Теорема 2. Пусть для задачи (1) выполнены исходные предположения и пусть 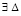 , такое, что
, такое, что 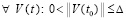 неравенства
неравенства 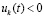 ,
, 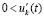 и соотношения
и соотношения
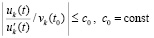 ,
, 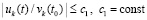 выполняются
выполняются
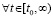 ,
, 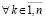 . Тогда нулевое решение задачи (1) устойчиво, при этом
. Тогда нулевое решение задачи (1) устойчиво, при этом 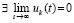 и
и 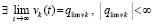 ,
,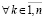 .
.
Аналогичные утверждения имеют место при условии 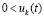 ,
, 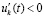 .
.
Доказательство. Пусть произвольно зафиксировано 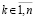 и рассматривается случай
и рассматривается случай 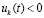 ,
, 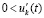 . Исходные предположения и неравенства
. Исходные предположения и неравенства 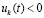 ,
, 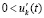
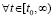 обеспечивают условия теоремы Коши о среднем значении [14] для функций vk(t) и uk(t)
обеспечивают условия теоремы Коши о среднем значении [14] для функций vk(t) и uk(t) 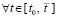 ,
, 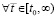 ,
, 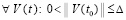 (функции vk(t) и uk(t) непрерывны на
(функции vk(t) и uk(t) непрерывны на 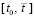 , дифференцируемы
, дифференцируемы 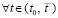 ,
, 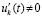
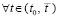 ). В силу этой теоремы
). В силу этой теоремы
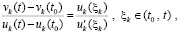
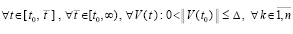 . (42)
. (42)
Из (42) 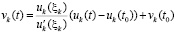 ,
,
поэтому 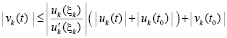 .
.
Неравенство 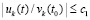 влечет
влечет 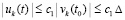 .
.
Отсюда
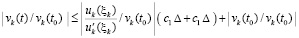 , где
, где 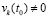 .
.
По условию первый сомножитель правой части неравенства ограничен константой c0, в результате 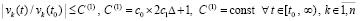 ,
,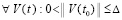 . Тем самым, с учетом произвольного выбора
. Тем самым, с учетом произвольного выбора 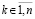 , выполнено (24), и по теореме 1 нулевое решение задачи (1) устойчиво. Далее, функция
, выполнено (24), и по теореме 1 нулевое решение задачи (1) устойчиво. Далее, функция 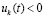 возрастает (
возрастает (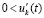 ). Следовательно,
). Следовательно, 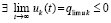 . Требуется доказать, что
. Требуется доказать, что 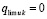 . Если предположить иное, то
. Если предположить иное, то 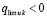 . Тогда uk(t) приближается к этому пределу, возрастая. Найдутся
. Тогда uk(t) приближается к этому пределу, возрастая. Найдутся 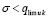 ,
, 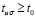 , такие, что
, такие, что  , при этом
, при этом 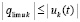 .
.
Очевидно, 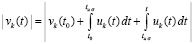 .
.
Отсюда 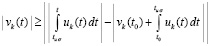 ,
,
где 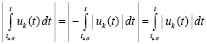 .
.
В результате 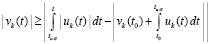 .
.
В то же время 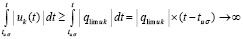 , если
, если 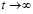 .
.
Отсюда 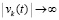 при t → ∞, что противоречит устойчивости нулевого решения. Таким образом, предположение
при t → ∞, что противоречит устойчивости нулевого решения. Таким образом, предположение 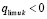 неверно, следовательно,
неверно, следовательно, 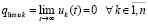 . Далее, в продолжение доказательства, случай, когда функция vk(t) не ограничена снизу, в условиях теоремы невозможен. Если допустить обратное, то эта функция монотонно убывает (
. Далее, в продолжение доказательства, случай, когда функция vk(t) не ограничена снизу, в условиях теоремы невозможен. Если допустить обратное, то эта функция монотонно убывает (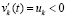 )
) 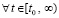 , и поскольку не ограничена снизу, то
, и поскольку не ограничена снизу, то 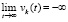 , что противоречит устойчивости нулевого решения. Остается принять, что функция vk(t) ограничена снизу, тогда в силу ее убывания
, что противоречит устойчивости нулевого решения. Остается принять, что функция vk(t) ограничена снизу, тогда в силу ее убывания 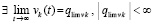 . Случай
. Случай 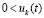 ,
, 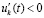 рассматривается аналогично. Теорема доказана.
рассматривается аналогично. Теорема доказана.
Из хода доказательства вытекает
Следствие 8. Все утверждения теоремы 2 сохранятся, если в условиях этой теоремы для некоторых компонентов системы (1) с номерами k = ki выполняются неравенства 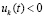 ,
, 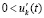 , а для остальных, с номерами
, а для остальных, с номерами 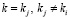 , выполняются неравенства
, выполняются неравенства 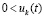 ,
, 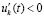 , те и другие в совокупности выполняются
, те и другие в совокупности выполняются 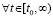 ,
,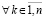 ,
, 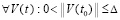 .
.
Имеет место
Теорема 3. Пусть выполнены все условия теоремы 2 и изменения условий, допустимые следствием 8. Тогда, если 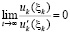 , где ξk из (42),
, где ξk из (42), 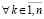 ,
, 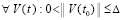 , то нулевое решение задачи (1) асимптотически устойчиво.
, то нулевое решение задачи (1) асимптотически устойчиво.
Доказательство. Пусть рассматриваются первоначальные условия теоремы 2 и случай 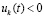 ,
, 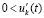
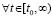 ,
,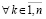 ,
, 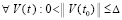 . По теореме 2 в этих условиях нулевое решение устойчиво,
. По теореме 2 в этих условиях нулевое решение устойчиво, 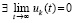 и
и 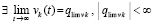 ,
, 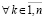 . Отсюда следует, что существует предел левой части (42) при t → ∞ и, в силу равенства в этом соотношении, существует предел правой части:
. Отсюда следует, что существует предел левой части (42) при t → ∞ и, в силу равенства в этом соотношении, существует предел правой части: 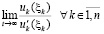 .
.
По условию доказываемой теоремы 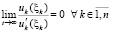 ,
, 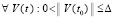 .
.
Пусть произвольно зафиксировано 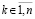 .
.
Требуется доказать, что 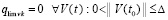 . Из (42)
. Из (42) 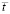 можно исключить, тогда
можно исключить, тогда
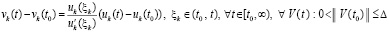 . (43)
. (43)
В (43) знак начального значения допустимо изменить на противоположный, положив 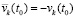 . Соответственные изменения всех переменных аналогично отмечаются чертой:
. Соответственные изменения всех переменных аналогично отмечаются чертой:
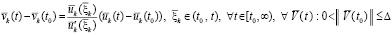 . (44)
. (44)
При этом для 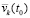 и
и 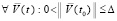 сохраняются все условия теоремы 2 и доказываемой теоремы, поскольку они предполагались выполненными
сохраняются все условия теоремы 2 и доказываемой теоремы, поскольку они предполагались выполненными 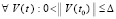 . Если теперь предположить противоположное тому, что надо доказать, именно, что
. Если теперь предположить противоположное тому, что надо доказать, именно, что 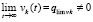 , то правомерны приводимые ниже рассуждения и оценки, вследствие которых предельный переход в равенстве приведет к противоречию. Равенства (43) и (44) складываются, с учетом
, то правомерны приводимые ниже рассуждения и оценки, вследствие которых предельный переход в равенстве приведет к противоречию. Равенства (43) и (44) складываются, с учетом 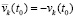 получится
получится
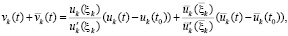
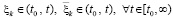 . (45)
. (45)
По теореме Лагранжа о среднем 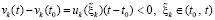 , с учетом
, с учетом 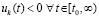 . Аналогично,
. Аналогично, 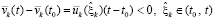 . Сложение этих отрицательных функций с учетом
. Сложение этих отрицательных функций с учетом 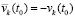 даст в сумме отрицательную функцию:
даст в сумме отрицательную функцию: 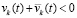 . Одно из слагаемых левой части неравенства (левой части (45)) является всюду отрицательной на полуоси функцией, такой, что ее модуль строго больше модуля начального значения
. Одно из слагаемых левой части неравенства (левой части (45)) является всюду отрицательной на полуоси функцией, такой, что ее модуль строго больше модуля начального значения 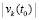 . Именно, это та функция, которая соответствует отрицательному начальному значению. Одно из пары начальных значений отрицательно в силу
. Именно, это та функция, которая соответствует отрицательному начальному значению. Одно из пары начальных значений отрицательно в силу 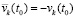 . Рассматриваемая функция убывает вследствие
. Рассматриваемая функция убывает вследствие 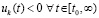 . Отсюда
. Отсюда 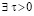 , такое, что в пределе по t → ∞ эта функция не превзойдет
, такое, что в пределе по t → ∞ эта функция не превзойдет 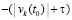 . Другое слагаемое левой части (45) также убывает, по такой же причине, и либо начиная с некоторого места такое слагаемое всюду отрицательно на полуоси, либо изначально всюду на полуоси неотрицательно, но вследствие убывания его модуль будет строго меньше модуля начального значения
. Другое слагаемое левой части (45) также убывает, по такой же причине, и либо начиная с некоторого места такое слагаемое всюду отрицательно на полуоси, либо изначально всюду на полуоси неотрицательно, но вследствие убывания его модуль будет строго меньше модуля начального значения 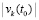 . Отсюда
. Отсюда 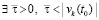 , такое, что в случае неотрицательности в пределе по t → ∞ эта функция не превосходит
, такое, что в случае неотрицательности в пределе по t → ∞ эта функция не превосходит 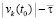 . В результате сумма
. В результате сумма 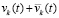 строго меньше нуля, причем либо в пределе по t → ∞ она не больше
строго меньше нуля, причем либо в пределе по t → ∞ она не больше 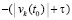 , либо в пределе по t → ∞ она не больше
, либо в пределе по t → ∞ она не больше 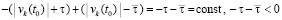 . В любом случае
. В любом случае
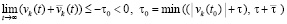 .
.
Предельный переход в равенстве (45) влечет
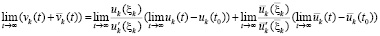 ,
,
где пределы дробей существуют и по условию равны нулю, кроме того, согласно теореме 2, 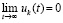 ,
, 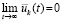 . В результате правая часть равенства равна нулю.
. В результате правая часть равенства равна нулю.
Тогда 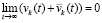 , однако было показано, что
, однако было показано, что 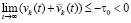 .
.
Полученное противоречие разрешается, если 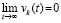 и
и 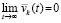 , так что
, так что 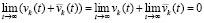 . Следовательно, предположение
. Следовательно, предположение 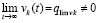 неверно. В результате
неверно. В результате 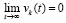 , где
, где 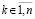 – произвольно выбранный номер компонента ненулевого решения. Равенство выполняется
– произвольно выбранный номер компонента ненулевого решения. Равенство выполняется 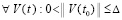 , поэтому в качестве ∆1 можно взять ∆. Нулевое решение задачи (1) устойчиво и
, поэтому в качестве ∆1 можно взять ∆. Нулевое решение задачи (1) устойчиво и 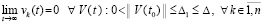 , так что это решение асимптотически устойчиво. Другие варианты условий рассматриваются аналогично. Теорема доказана.
, так что это решение асимптотически устойчиво. Другие варианты условий рассматриваются аналогично. Теорема доказана.
Пусть снова произвольно зафиксировано 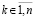 и рассматривается случай
и рассматривается случай 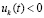 ,
, 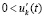
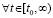 . В условиях теоремы 3 выполнено
. В условиях теоремы 3 выполнено 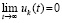 ,
, 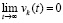 , согласно условиям
, согласно условиям 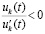 .
.
Если 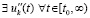 , очевидно,
, очевидно, 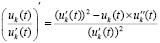 , где
, где 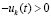 .
.
Если при этом 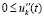 , то
, то 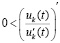 . Тогда функция
. Тогда функция 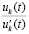 возрастает, при этом ограничена сверху
возрастает, при этом ограничена сверху 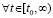 .
.
Следовательно, 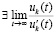 ,
, 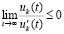 .
.
То же получится, если 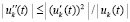 .
.
Пусть теперь рассматривается случай 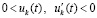
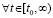 . По-прежнему
. По-прежнему 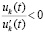 , но
, но 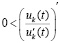 при условии
при условии 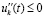 , или, если
, или, если 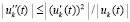 , далее сохраняются предыдущие рассуждения. Рассуждения распространяются на условия следствия 8.
, далее сохраняются предыдущие рассуждения. Рассуждения распространяются на условия следствия 8.
Отсюда вытекает
Следствие 9. Пусть выполнены все условия теоремы 3 и рассматривается случай 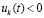 ,
, 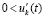
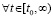 ,
, 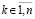 . Если
. Если 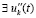 , и при этом
, и при этом 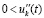
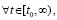
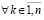 , то выполнены условия применения правила Лопиталя, согласно которому
, то выполнены условия применения правила Лопиталя, согласно которому 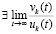 и
и
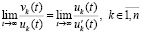 . (46)
. (46)
В случае 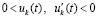
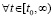 тот же результат получится, если
тот же результат получится, если 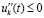 . В обоих случаях результат сохранится, если
. В обоих случаях результат сохранится, если 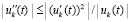 .
.
В (46) 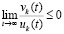 и
и 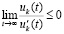
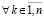 , поэтому решение vk(t) в условиях следствия не может иметь одинакового знака с uk(t). Все утверждения данного следствия сохраняются
, поэтому решение vk(t) в условиях следствия не может иметь одинакового знака с uk(t). Все утверждения данного следствия сохраняются 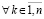 в условиях следствия 8.
в условиях следствия 8.
Если в (42) знаменатель дроби равномерно отделен от нуля,
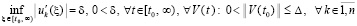 , (47)
, (47)
то, как нетрудно видеть, теоремы 2, 3 можно объединить с упрощением условий.
Теорема 4. Пусть для задачи (1) выполнены исходные предположения и, кроме того, выполняется (47). Пусть 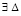 , такое, что
, такое, что 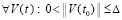 неравенства
неравенства 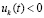 ,
, 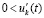 , а также соотношения
, а также соотношения 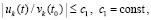 выполняются
выполняются 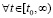 ,
,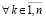 . Тогда нулевое решение задачи (1) устойчиво, при этом
. Тогда нулевое решение задачи (1) устойчиво, при этом 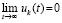
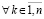 , и если
, и если 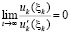 , где ξk из (42),
, где ξk из (42), 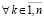 ,
, 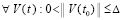 , то оно асимптотически устойчиво. Аналогичные утверждения верны в случае
, то оно асимптотически устойчиво. Аналогичные утверждения верны в случае 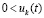 ,
, 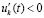 и сохраняются при изменениях условий следствия 8.
и сохраняются при изменениях условий следствия 8.
Замечание 4. Теоремы 3 и 4 сохранят свои утверждения, если в их условиях соотношение 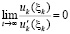 заменить соотношением
заменить соотношением
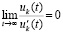 , (48)
, (48)
поскольку значения 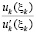 образуют числовую подпоследовательность некоторой сходящейся последовательности
образуют числовую подпоследовательность некоторой сходящейся последовательности 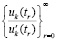 , образованной значениями независимой переменной t, – такими, что
, образованной значениями независимой переменной t, – такими, что 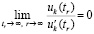 . По теореме 2
. По теореме 2 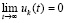 , отсюда (48) будет выполняться, если
, отсюда (48) будет выполняться, если 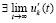 и
и 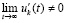 . Поэтому теоремы 3 и 4 сохранятся, если вместо (48) в их условиях потребовать существования
. Поэтому теоремы 3 и 4 сохранятся, если вместо (48) в их условиях потребовать существования 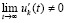 .
.
С учетом этого замечания теорема 3 перейдет в следующую теорему.
Теорема 5. Пусть для задачи (1) выполнены исходные предположения. Пусть 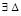 , такое, что
, такое, что 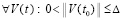 неравенства
неравенства 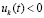 ,
, 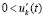 , а также соотношения
, а также соотношения 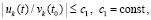 выполняются
выполняются 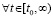 ,
,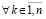 . Тогда нулевое решение задачи (1) устойчиво, при этом
. Тогда нулевое решение задачи (1) устойчиво, при этом 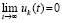
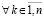 . Если, кроме того,
. Если, кроме того, 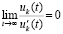 или если
или если 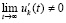
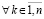 ,
, 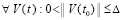 , то нулевое решение асимптотически устойчиво. Аналогичные утверждения верны в случае
, то нулевое решение асимптотически устойчиво. Аналогичные утверждения верны в случае 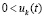 ,
, 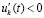 и сохраняются при изменениях условий, допустимых следствием 8.
и сохраняются при изменениях условий, допустимых следствием 8.
Производная компонента 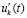 из (1) аналитически определяется по формуле полной производной сложной функции [14]
из (1) аналитически определяется по формуле полной производной сложной функции [14]
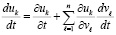 , или
, или 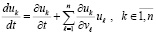 .
.
В случае выполнения (47) условия устойчивости можно сформулировать без предположения о постоянстве знаков uk(t) и u'k(t). Имеет место
Предложение 2. Пусть для задачи (1) выполнены исходные предположения и пусть 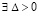 , такое, что
, такое, что 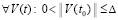 неравенства
неравенства 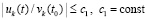 , выполняются
, выполняются 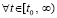 ,
,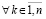 . Пусть, кроме того, выполняется соотношение (47) и выполнены условия теоремы Коши в форме (42). Тогда нулевое решение задачи (1) устойчиво. Утверждение сохраняется при изменениях условий, допустимых следствием 8.
. Пусть, кроме того, выполняется соотношение (47) и выполнены условия теоремы Коши в форме (42). Тогда нулевое решение задачи (1) устойчиво. Утверждение сохраняется при изменениях условий, допустимых следствием 8.
Доказательство. По условию (42) верно 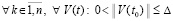 , что влечет
, что влечет
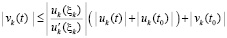 .
.
Из 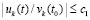 следует
следует 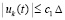 .
.
Отсюда 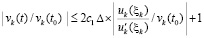 , где
, где 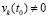 .
.
Далее, 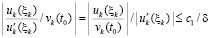 , где δ из (47).
, где δ из (47).
В результате 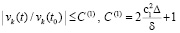 ,
,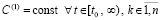 ,
, 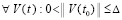 , что означает выполнение (24) в условиях теоремы 1.
, что означает выполнение (24) в условиях теоремы 1.
Поэтому нулевое решение задачи (1) устойчиво. Предложение доказано.
Выражение vk(t) из (42) влечет формально общий вид условий устойчивости.
Предложение 3. Пусть для задачи (1) выполнены условия применения теоремы Коши в форме (42). Тогда для устойчивости нулевого решения необходимо и достаточно существование 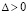 , такого, что
, такого, что 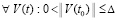 выполняется соотношение
выполняется соотношение
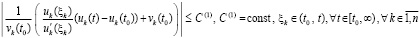 .
.
Для асимптотической устойчивости нулевого решения необходимо и достаточно, чтобы оно было устойчиво и существовало 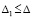 , такое, что
, такое, что 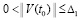 влечет
влечет
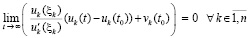 .
.
Утверждения предложения сохраняются в условиях следствия 8.
Достаточное условие неустойчивости включает
Теорема 6. Пусть для задачи (1) выполнены исходные предположения. Если 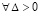 можно указать
можно указать 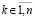 , такое, что неравенства
, такое, что неравенства 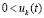 и
и 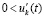 выполняются
выполняются 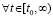 ,
, 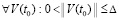 , то нулевое решение задачи (1) неустойчиво. Утверждение сохраняется, если в тех же условиях
, то нулевое решение задачи (1) неустойчиво. Утверждение сохраняется, если в тех же условиях 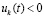 и
и 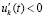
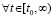 ,
, 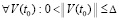 .
.
Доказательство. Пусть 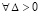 для номера
для номера 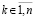 неравенства
неравенства 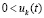 и
и 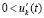 выполняются
выполняются 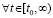 ,
, 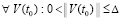 . Тогда с учетом исходных предположений выполнены условия теоремы Коши, в силу которой верно (42). В рассматриваемых условиях uk(t) монотонно возрастает (
. Тогда с учетом исходных предположений выполнены условия теоремы Коши, в силу которой верно (42). В рассматриваемых условиях uk(t) монотонно возрастает (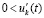 ) и, в силу
) и, в силу 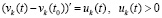 , монотонно возрастает функция
, монотонно возрастает функция 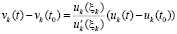 . При этом по монотонности
. При этом по монотонности 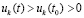 , так что
, так что 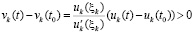 . Отсюда, в силу монотонного роста, найдутся
. Отсюда, в силу монотонного роста, найдутся 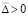 и
и 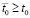 , такие, что
, такие, что 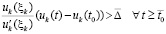 , тогда
, тогда 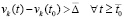 . Можно считать априори выбранным значение
. Можно считать априори выбранным значение 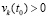 , при этом оно может быть сколь угодно мало. Тогда
, при этом оно может быть сколь угодно мало. Тогда 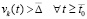 , следовательно,
, следовательно, 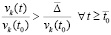 , и
, и 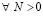 , где N может иметь сколь угодно большое числовое значение, выполняется
, где N может иметь сколь угодно большое числовое значение, выполняется 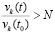 лишь только
лишь только 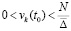 . Тем самым нарушается (24) – необходимое условие устойчивости теоремы 1. Поэтому нулевое решение задачи (1) неустойчиво. Случай
. Тем самым нарушается (24) – необходимое условие устойчивости теоремы 1. Поэтому нулевое решение задачи (1) неустойчиво. Случай 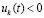 и
и 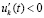
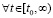 рассматривается аналогично. Теорема доказана.
рассматривается аналогично. Теорема доказана.
Необходимо заметить, что условия теоремы Коши исключают смену знака в знаменателе левой части (42), а условие (47) – смену знака в правой части (42). Поэтому рассмотренные утверждения носят ограниченный характер, они не выводят из области постоянства знаков компонентов правой части (1), их нельзя перенести на общий случай переменных знаков функций uk(t) и 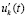 в произвольных точках полуоси. Значение утверждений можно видеть в том, что на их основе строятся знакопостоянные мажоранты для знакопеременных компонентов правых частей системы (1) в условиях предложения 1. Чтобы при этом аналитически учитывать обратную пропорцию начальным значениям, можно выполнить переход к интегральной форме мажорирующих функций с заменой переменной согласно (37), (38).
в произвольных точках полуоси. Значение утверждений можно видеть в том, что на их основе строятся знакопостоянные мажоранты для знакопеременных компонентов правых частей системы (1) в условиях предложения 1. Чтобы при этом аналитически учитывать обратную пропорцию начальным значениям, можно выполнить переход к интегральной форме мажорирующих функций с заменой переменной согласно (37), (38).
Общие условия устойчивости с обратной пропорцией начальным значениям компонентов правой части. Пусть на полуоси последовательными индексами отмечены равные по длине отрезки с общими границами
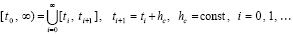 , (49)
, (49)
где hc задается произвольно. Искомая оценка устойчивости будет опираться на теорему Лагранжа о среднем, применяемую к каждому отрезку из (49). Для решения задачи (1) будут рассматриваться следующие разновидности формул средних значений
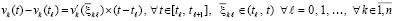 , (50)
, (50)
или
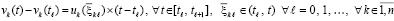 , (51)
, (51)
а также
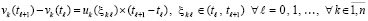 . (52)
. (52)
Имеет место
Теорема 7. Пусть для задачи (1) выполнены исходные предположения. Пусть предполагается, кроме того, что в условиях разбиения (49), при любом выборе 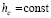 ,
, 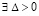 , такое, что
, такое, что 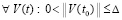 ,
,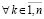 , выполняются неравенства
, выполняются неравенства
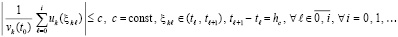 , (53)
, (53)
где 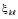 из (52), аналогично, для каждого слагаемого из левой части (53)
из (52), аналогично, для каждого слагаемого из левой части (53)
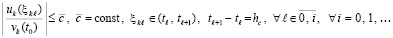 . (54)
. (54)
Тогда нулевое решение задачи (1) устойчиво.
Доказательство. Пусть в (49) hc произвольно выбрано и зафиксировано. Пусть произвольно зафиксировано 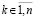 . Исходные предположения для функции vk(t) обеспечивают выполнение условий теоремы Лагранжа о среднем на каждом отрезке из (49), в частности выполняются соотношения (50)–(52). Из (52) при
. Исходные предположения для функции vk(t) обеспечивают выполнение условий теоремы Лагранжа о среднем на каждом отрезке из (49), в частности выполняются соотношения (50)–(52). Из (52) при 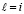
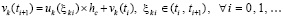 (55)
(55)
Из (55) 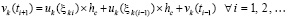 , и, далее, по рекуррентности,
, и, далее, по рекуррентности,
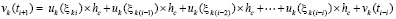 . (56)
. (56)
Отсюда
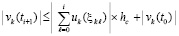 . (57)
. (57)
Из (57) 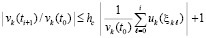 .
.
Отсюда, с учетом (53), 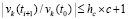 . Для оценки
. Для оценки 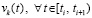 , используется неравенство
, используется неравенство 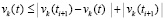 , согласно которому с учетом (51)
, согласно которому с учетом (51) 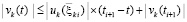 , где
, где 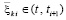 . Далее, с учетом (53),
. Далее, с учетом (53), 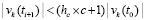 . В результате
. В результате 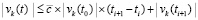 , где
, где 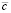 из (54), и
из (54), и
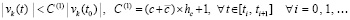 . (58)
. (58)
Окончательно
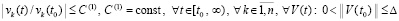 . (59)
. (59)
Выполнено соотношение (24) теоремы 1, и рассматриваемая теорема доказана.
Замечание 5. Теорема 7 не требует выполнения всех исходных предположений – при ее доказательстве, до оценки (58) включительно, нигде не использовалось предположение непрерывной дифференцируемости правой части (1). В условиях теоремы достаточно было бы ограничиться непрерывностью правой части, при этом из (58) непосредственно вытекает устойчивость нулевого решения задачи (1). Формально дифференцируемость U(t) была нужна в доказательстве как часть условия теоремы 1 – для ссылки на (24) исходя из (59), но фактически (59) излишне – устойчивость непосредственно следует из (58): 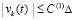 .
.
Имеет место
Теорема 8. Пусть выполнены все условия теоремы 7. Если, кроме того, 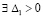 ,
, 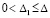 , такое, что при любом выборе
, такое, что при любом выборе 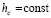 из (49),
из (49),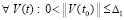 выполняются соотношения
выполняются соотношения
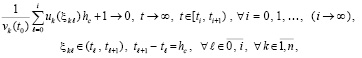 (60)
(60)
где 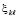 из (52), а также
из (52), а также
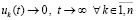 , (61)
, (61)
то нулевое решение задачи (1) асимптотически устойчиво.
Доказательство. Пусть произвольно зафиксировано 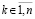 . По теореме 7 нулевое решение задачи (1) устойчиво. Имеет место разложение (56), для которого верно равенство
. По теореме 7 нулевое решение задачи (1) устойчиво. Имеет место разложение (56), для которого верно равенство
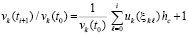 .
.
Отсюда и из (60)
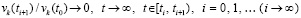 . (62)
. (62)
Очевидно, 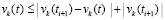 ,
, 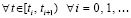 , следовательно,
, следовательно, 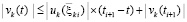 , где
, где 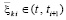 из (51).
из (51).
Отсюда 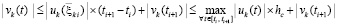 .
.
По условию 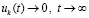 , поэтому
, поэтому 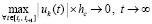 . Кроме того, согласно (62)
. Кроме того, согласно (62) 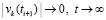 . В результате
. В результате
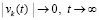 . (63)
. (63)
Соотношение (63) получено 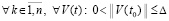 , в качестве ∆1 можно взять ∆1 = ∆. Окончательно
, в качестве ∆1 можно взять ∆1 = ∆. Окончательно 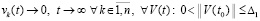 .
.
Теорема доказана.
Замечание 6. В условиях теоремы 8 стремление к нулю решения следует из стремления к нулю производной в (61), а также из существования предела суммы производных равного 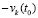 в (60), где производные слагаемых взяты из (52).
в (60), где производные слагаемых взяты из (52).
Разложение (56) допускает различные оценки сверху, (57) – одна из них. Можно находить разнообразные мажоранты для (56) или (57) с целью получить достаточные условия устойчивости. В частности, (57) вытекает из неравенств
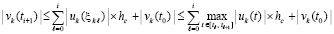 . (64)
. (64)
Если uk(t) такова, что
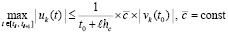 , (65)
, (65)
то этого недостаточно для устойчивости, требуется усиление неравенства. Из (65)
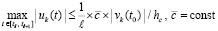 ,
,
и 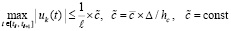 .
.
Подстановка в (64) влечет
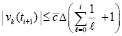 (66)
(66)
Поскольку 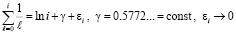 [15], то вместо мажоранты из (66) можно рассмотреть частное от деления на
[15], то вместо мажоранты из (66) можно рассмотреть частное от деления на 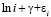 (с точностью до постоянного множителя) –
(с точностью до постоянного множителя) –
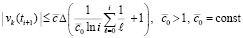 , (67)
, (67)
что повлечет 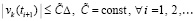 .
.
Отсюда последует 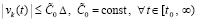 , что будет означать устойчивость нулевого решения задачи (1) при условии
, что будет означать устойчивость нулевого решения задачи (1) при условии
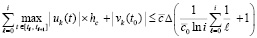 ,
,
где константы взяты из (67), учтено (64) и значение i предполагается достаточно большим. Наряду с этим как достаточное условие устойчивости нулевого решения задачи (1) можно рассматривать соотношение
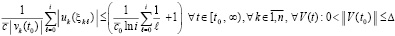 . (68)
. (68)
С точностью до постоянного множителя 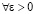 , начиная с некоторого i, выполняется
, начиная с некоторого i, выполняется
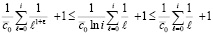 ,
,
поэтому правая часть (68) имеет промежуточный порядок роста между гармоническим и субгармоническим рядом.
На основе (49)–(52) и (56) можно сформулировать необходимые и достаточные условия устойчивости. Пусть снова произвольно зафиксировано 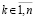 . Если (51) преобразовать к виду
. Если (51) преобразовать к виду 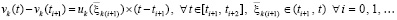 и сложить с (56), то равенство сохранится:
и сложить с (56), то равенство сохранится:
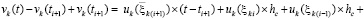
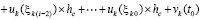 .
.
В результате
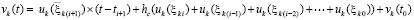 ,
,
где 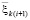 из (51) при
из (51) при 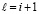 ,
, 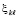 из (52) при
из (52) при 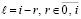 .
.
Деление на vk(t0) влечет
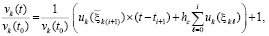
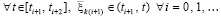 (69)
(69)
Согласно (49) равенство (69) верно 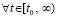 . Преобразования, в результате которых получено (69), верны
. Преобразования, в результате которых получено (69), верны 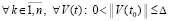 . Отсюда, с учетом замечания 5, вытекает
. Отсюда, с учетом замечания 5, вытекает
Теорема 9. Пусть для задачи (1) выполнены исходные предположения (за вычетом предположения о непрерывной дифференцируемости 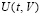 ). Пусть выполнено разбиение (49), где
). Пусть выполнено разбиение (49), где 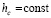 выбрано произвольно. Тогда для устойчивости нулевого решения задачи (1) необходимо и достаточно существование
выбрано произвольно. Тогда для устойчивости нулевого решения задачи (1) необходимо и достаточно существование 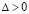 , такого, что
, такого, что 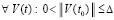 ,
, 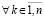 , имеет место соотношение
, имеет место соотношение
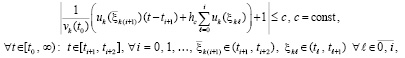 (70)
(70)
где 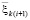 из (51) при
из (51) при 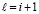 ,
, 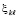
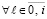 – из (52). Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось это условие и существовало
– из (52). Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось это условие и существовало 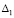 ,
, 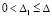 , такое, что
, такое, что 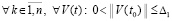 верно соотношение
верно соотношение
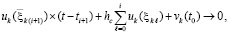 (71)
(71)
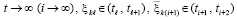 .
.
Замечание 7. Необходимо принять во внимание разницу между теоремой 9 и леммой 2. В отличие от (22) соотношение (70) использует точные значения 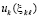 компонентов правой части (1),
компонентов правой части (1), 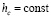 , и не предполагает перехода к пределу по h → 0. Кроме того, (70) не использует дифференцируемости uk(t) из (1). То же можно сказать относительно сопоставления (23) и (70), (71).
, и не предполагает перехода к пределу по h → 0. Кроме того, (70) не использует дифференцируемости uk(t) из (1). То же можно сказать относительно сопоставления (23) и (70), (71).
Теорема 9, в выражении через компоненты правой части (1), при условии их непрерывности на полуоси, дает необходимые и достаточные условия устойчивости и асимптотической устойчивости нулевого решения задачи (1) для системы ОДУ общего вида в предположении существования и единственности решения в R0.
Замечание 8. Равенство (56), левые части (70) и (71) близко связаны с теоремой о среднем, в том числе применительно к значению интеграла. Они также сходны с разложением (22) и с интегральной суммой, определяющей интеграл [15]. Существенное отличие в том, что в (70) используется обратная пропорция значению vk(t0), произвольно выбранному из неравенства 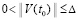 . Отличие, кроме того, в том, что рассматриваемые соотношения применяются для оценки устойчивости решения ОДУ.
. Отличие, кроме того, в том, что рассматриваемые соотношения применяются для оценки устойчивости решения ОДУ.
Для практических целей существует возможность определить значения 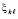 в
в 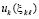 с высокой точностью. Именно, из (52)
с высокой точностью. Именно, из (52)
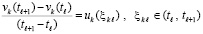 ,
,
или 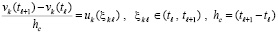 ,
,
что равносильно 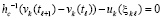 . Отсюда найти
. Отсюда найти 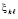 можно как минимум модуля левой части равенства
можно как минимум модуля левой части равенства
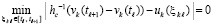 . (72)
. (72)
Все значения под знаком модуля в (72) представимы в компьютерной реализации приближенного решения задачи (1). Минимум модуля любой функции на любом конечном отрезке с высокой точностью определяется с помощью программы на основе алгоритма сортировки [16].
Ниже материал дополняется особенностями оценок устойчивости линейных систем.
Об устойчивости линейной системы ОДУ. Наблюдается аналогия между решением системы линейных алгебраических уравнений (СЛАУ) по методу простой итерации и решением задачи Коши для линейной системы ОДУ с постоянными коэффициентами по методу Эйлера. Пусть рассматривается СЛАУ в приведенной форме
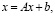 (73)
(73)
где матрица A = (aij), n×n, общего вида, 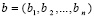 ,
, 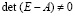 ,
, 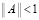 , E – единичная матрица. В этих условиях метод простой итерации
, E – единичная матрица. В этих условиях метод простой итерации
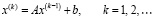 . (74)
. (74)
сходится к единственному решению СЛАУ (73) при любом выборе 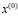 . Количество итераций (74) можно сократить, возводя матрицу в степень. Так, если найти
. Количество итераций (74) можно сократить, возводя матрицу в степень. Так, если найти 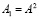 и
и 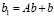 , то (74) эквивалентно схеме
, то (74) эквивалентно схеме 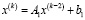 , число итераций которой вдвое меньше, чем в (74). Аналогично,
, число итераций которой вдвое меньше, чем в (74). Аналогично, 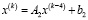 , где
, где 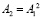 ,
, 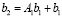 , и число последующих итераций сократится вчетверо и т.д. В случае параллельного вычисления требуемых степеней матриц и соответственных векторов, путем данных преобразований можно существенно сократить время решения системы (73). В общем случае итерационная схема решения СЛАУ с логарифмическим числом итераций записывается следующим образом
, и число последующих итераций сократится вчетверо и т.д. В случае параллельного вычисления требуемых степеней матриц и соответственных векторов, путем данных преобразований можно существенно сократить время решения системы (73). В общем случае итерационная схема решения СЛАУ с логарифмическим числом итераций записывается следующим образом
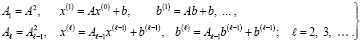 (75)
(75)
Схема (75) эквивалентна (74) [17]. При этом если в (74) для произвольного 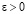
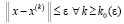 , (76)
, (76)
то для 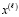 из (75) то же верно
из (75) то же верно 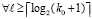 , число итераций k сокращается до
, число итераций k сокращается до 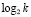 . Однако итерации (75) существенно сложнее. Максимально параллельное выполнение одной итерации (74) и одного шага (75) происходит за одинаковое время (здесь время – синоним временной сложности). Шаг (75) выполняется за время
. Однако итерации (75) существенно сложнее. Максимально параллельное выполнение одной итерации (74) и одного шага (75) происходит за одинаковое время (здесь время – синоним временной сложности). Шаг (75) выполняется за время 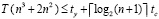 , шаг (74) – за время
, шаг (74) – за время 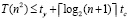 , где tc и ty – время арифметического сложения и умножения, в скобках левой части – число процессоров. В результате метод (75) достигает приближения (76) к решению СЛАУ (73) за время
, где tc и ty – время арифметического сложения и умножения, в скобках левой части – число процессоров. В результате метод (75) достигает приближения (76) к решению СЛАУ (73) за время
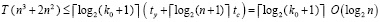 .
.
Пусть теперь рассматривается задача Коши для линейной системы ОДУ
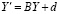 ,
, 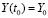 , (77)
, (77)
с матрицей постоянных коэффициентов B, n×n, и постоянным вектором d, Y = Y(t) 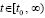 . Для приближенного решения (77) применяется метод Эйлера
. Для приближенного решения (77) применяется метод Эйлера
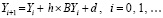 , или,
, или,
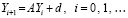 , (78)
, (78)
где 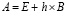 , шаг h определяется из (3). Внешне (78) сходно с (74). Устойчивость линейной системы совпадает с устойчивостью соответствующей однородной системы
, шаг h определяется из (3). Внешне (78) сходно с (74). Устойчивость линейной системы совпадает с устойчивостью соответствующей однородной системы 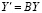 , поэтому ниже полагается
, поэтому ниже полагается 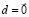 . Схема (78) примет вид
. Схема (78) примет вид
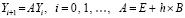 . (79)
. (79)
Метод Эйлера рассматривается в условиях сходимости, поэтому в (79)
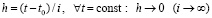 . (80)
. (80)
Если теперь по аналогии с (75) возводить матрицу A в степень, то сокращение числа итераций не произойдет, и это было бы излишне для пошагового приближения решения ОДУ, однако при фиксированном h происходит удаление Yi+1 от начальной точки t0 в геометрической прогрессии:
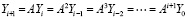 . (81)
. (81)
Фиксирование h нарушает (80), но при достаточно малом h реализуется численное моделирование устойчивости линейной системы. Удобно выполнять умножение текущей матрицы на себя, моделирующий процесс примет вид
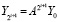 . (82)
. (82)
Из (81), (82) поведение 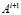 (
(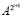 ) на полуоси полностью определяет рост, ограниченность или убывание возмущения нулевого решения при условии, что шаг из (80). Процесс следует рассматривать при произвольном t как
) на полуоси полностью определяет рост, ограниченность или убывание возмущения нулевого решения при условии, что шаг из (80). Процесс следует рассматривать при произвольном t как 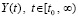 , (81) переходит в соотношение
, (81) переходит в соотношение
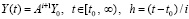 , (83)
, (83)
точное значение решения для любого t получается путем предельного перехода
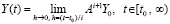 ,
,
что эквивалентно
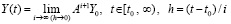 . (84)
. (84)
Из (84) именно асимптотическое поведение 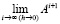 полностью определяет характер устойчивости нулевого решения, соответственно – всей системы [1]. Отсюда вытекает
полностью определяет характер устойчивости нулевого решения, соответственно – всей системы [1]. Отсюда вытекает
Теорема 10. Для устойчивости системы (77) необходимо и достаточно, чтобы
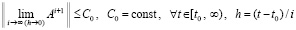 , (85)
, (85)
где 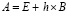 . Если условие (85) выполняется, то для асимптотической устойчивости системы необходимо и достаточно, чтобы
. Если условие (85) выполняется, то для асимптотической устойчивости системы необходимо и достаточно, чтобы
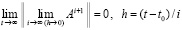 . (86)
. (86)
Следствие 10. Теорема сохраняется, если в (85) и в (86) 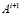 заменить на
заменить на 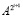 и
и 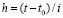 заменить на
заменить на 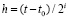 .
.
В случае если система (77) линейна, но матрица B не постоянна, B = B(t), все элементы B(t) предполагаются непрерывными функциями на полуоси, что влечет равномерную сходимость метода Эйлера 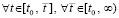 . Выполняется переход от (78) к (79), (80). Поскольку теперь матрица
. Выполняется переход от (78) к (79), (80). Поскольку теперь матрица 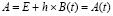 переменная, переход к (83) невозможен. Аналог предыдущего процесса строится пошагово. Пусть в (80) t обозначается как ti:
переменная, переход к (83) невозможен. Аналог предыдущего процесса строится пошагово. Пусть в (80) t обозначается как ti:
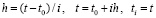 .
.
Вместо (81) получится 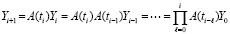 . Отсюда вытекает
. Отсюда вытекает
Теорема 11. Для устойчивости линейной системы (77) с матрицей B = B(t), все элементы которой непрерывны 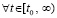 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
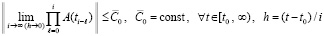 , (87)
, (87)
где 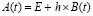 ,
, 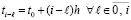 . Если это условие выполнено, то для асимптотической устойчивости необходимо и достаточно, чтобы при h из (87) выполнялось
. Если это условие выполнено, то для асимптотической устойчивости необходимо и достаточно, чтобы при h из (87) выполнялось
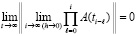 . (88)
. (88)
Замечание 9. Описанные ранее способы анализа устойчивости, независимо от способов теорем 8, 9, могут использоваться для задачи (77) как для частного случая задачи (1).
Численное моделирование устойчивости системы (77) на основе (85), (86) и (87), (88) при малом h на большом интервале, как правило, соответствует аналитической оценке устойчивости [17]. Стоит дополнить, что методом на основе сортировки, упоминавшемся относительно (72), можно с высокой точностью вычислить все корни характеристического полинома матрицы B из (77) [16] и на этой основе сделать полный вывод об устойчивости системы.
О линеаризации системы ОДУ для оценки устойчивости. Пусть для приближенного решения задачи (1) применяется кусочно-интерполяционный метод с итерационным уточнением [18, 19]. На каждом подынтервале интерполирующие компоненты правой части полиномы имеют вид алгебраических полиномов фиксированной степени от одной переменной t, они непрерывно склеиваются на каждой границе смежных подынтервалов. В результате получается непрерывное приближение функцией одной переменной каждого компонента правой части системы (1) на всем отрезке приближенного решения. Приближение выполняется с наперед заданной точностью. Система (1) оказывается преобразованной к приближению линейной системой вида (77), где матрица B = B(t) непрерывна на всем отрезке приближения. С априори заданной точностью приближается также само решение. Массивы полиномов, приближающих правую часть и приближающих решение на промежутке большой длины, можно хранить в виде типизированных файлов. В результате достигается возможность численного моделирования устойчивости решения задачи (1) на основе преобразования к линеаризованной системе. Ниже описание метода детализируется согласно [19]. В (1) меняется обозначение независимой переменной:
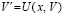 ,
, 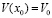 ,
, 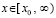 , (89)
, (89)
где 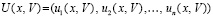 ,
, 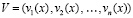 ,
, 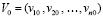 . Отрезок приближенного решения разбивается на подынтервалы равной длины
. Отрезок приближенного решения разбивается на подынтервалы равной длины
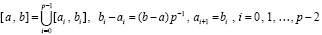 . (90)
. (90)
Пусть произвольно зафиксировано 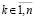 . Выполняется приближение функции uk(x) из (89) на [a, b] из (90). Для этого на каждом подынтервале
. Выполняется приближение функции uk(x) из (89) на [a, b] из (90). Для этого на каждом подынтервале 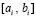 строится интерполяционный полином Ньютона степени
строится интерполяционный полином Ньютона степени 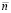 с равноотстоящими узлами для интерполирования uk(x):
с равноотстоящими узлами для интерполирования uk(x):
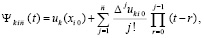 (91)
(91)
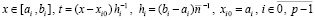 .
.
Полином (91) преобразуется к виду полинома с числовыми коэффициентами
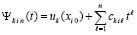 , (92)
, (92)
где 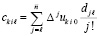 . В основе преобразования – алгоритм восстановления коэффициентов полинома по его корням [18], согласно которому в
. В основе преобразования – алгоритм восстановления коэффициентов полинома по его корням [18], согласно которому в 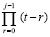 следует положить
следует положить 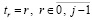 , значения коэффициентов рекуррентно восстанавливаются из соотношений
, значения коэффициентов рекуррентно восстанавливаются из соотношений
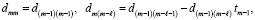 (93)
(93)
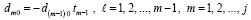 .
.
Здесь и ниже 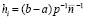 . Интерполирование выполняется с рядом особенностей.
. Интерполирование выполняется с рядом особенностей.
В 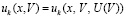 подставляется приближенное значение
подставляется приближенное значение 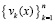 , вначале
, вначале 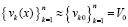 . Функция
. Функция 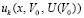 приближается полиномами (92) по схеме (91)–(93) с итерационным уточнением по следующему алгоритму. При фиксированных значениях
приближается полиномами (92) по схеме (91)–(93) с итерационным уточнением по следующему алгоритму. При фиксированных значениях 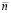 и p из (90) на отрезке
и p из (90) на отрезке 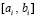 , сначала при i = 0, затем, аналогично, при
, сначала при i = 0, затем, аналогично, при 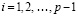 , выполняется приближение (92),
, выполняется приближение (92),
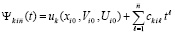 ,
, 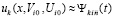 ,
, 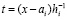 ,
,
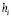 – шаг интерполяции на
– шаг интерполяции на 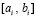 , постоянный для всех номеров i:
, постоянный для всех номеров i: 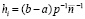 .
.
Первообразная
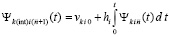 , или,
, или, 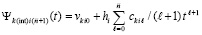 ,
,
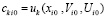 (на начальном подынтервале
(на начальном подынтервале 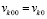 , на последующих подынтервалах выбор
, на последующих подынтервалах выбор 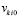 поясняется ниже), принимается за приближение k-го компонента решения:
поясняется ниже), принимается за приближение k-го компонента решения: 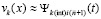 ,
, 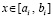 . Тогда
. Тогда 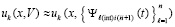 . При том же значении
. При том же значении 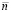 , на том же подынтервале строится интерполяционный полином вида (92) для приближения
, на том же подынтервале строится интерполяционный полином вида (92) для приближения 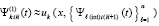 ,
, 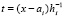 . От этого полинома снова берется первообразная с тем же значением константы
. От этого полинома снова берется первообразная с тем же значением константы 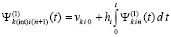 , выполняется соответственная подстановка в правую часть,
, выполняется соответственная подстановка в правую часть, 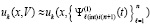 , которая затем аналогично интерполируется,
, которая затем аналогично интерполируется, 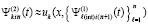 ,
, 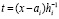 . Итерации
. Итерации
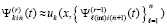 ,
, 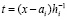 ,
,
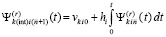 ,
, 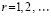 ,
,
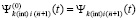 ,
, 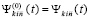
продолжаются до априори заданной границы: 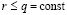 . Выше неявно предполагалось, что за значение
. Выше неявно предполагалось, что за значение 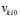 было взято
было взято 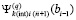 . По окончании итераций на
. По окончании итераций на 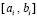 выполняется переход к
выполняется переход к 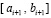 , где за значение
, где за значение 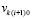 принимается
принимается 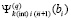 . Отсюда
. Отсюда 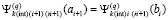 ,
, 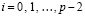 , и интегральные полиномы совпадают на каждой общей границе всех смежных подынтервалов. Таким образом, построенное приближение решения является непрерывной функцией
, и интегральные полиномы совпадают на каждой общей границе всех смежных подынтервалов. Таким образом, построенное приближение решения является непрерывной функцией 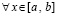 . Кусочно-интерполяционное приближение правой части (89) (производной от решения) также, по построению, является непрерывной функцией на всем
. Кусочно-интерполяционное приближение правой части (89) (производной от решения) также, по построению, является непрерывной функцией на всем 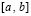 . Именно, интерполяция выполняется с равномерным шагом, в число интерполяционных узлов включаются обе границы подынтервала. За значение
. Именно, интерполяция выполняется с равномерным шагом, в число интерполяционных узлов включаются обе границы подынтервала. За значение 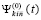 в интерполяционном узле на левой границе подынтервала
в интерполяционном узле на левой границе подынтервала 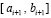 принимается выходное значение
принимается выходное значение  на правой границе подынтервала
на правой границе подынтервала  , и это узловое значение не меняется в продолжение итераций на
, и это узловое значение не меняется в продолжение итераций на  . В результате
. В результате  , полиномы, интерполирующие k-й компонент правой части (89), имеют равные значения на каждой общей границе смежных подынтервалов, что влечет непрерывность кусочной интерполяции компонентов правой части (1) на всем отрезке
, полиномы, интерполирующие k-й компонент правой части (89), имеют равные значения на каждой общей границе смежных подынтервалов, что влечет непрерывность кусочной интерполяции компонентов правой части (1) на всем отрезке 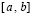 . На этом отрезке имеет место равномерная сходимость
. На этом отрезке имеет место равномерная сходимость 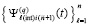 к решению V задачи (89) и равномерная сходимость
к решению V задачи (89) и равномерная сходимость 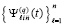 к производной от решения
к производной от решения  [18], если p → ∞.
[18], если p → ∞.
Однако для доказательства предполагается существование и непрерывность производных до 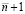 -го порядка включительно от uk(x),
-го порядка включительно от uk(x), 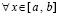 .
.
С отступлением от формализации имеют место следующие предложения [19].
Предложение 4. Коэффициенты полиномиального приближения производной от k-го компонента решения задачи (89), 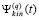 ,
,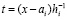 , имеют числовые значения,
, имеют числовые значения, 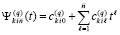 . По всем номерам подынтервалов из (90) они образуют массив из p строк вида
. По всем номерам подынтервалов из (90) они образуют массив из p строк вида 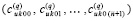 ,
,  , … ,
, … , 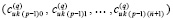 , который можно хранить в памяти компьютера в виде типизированного файла. Обращение к строке этого файла позволяет восстановить значение k-го компонента производной от решения по схеме Горнера. Номер строки типизированного файла, соответственной произвольному значению независимой переменной
, который можно хранить в памяти компьютера в виде типизированного файла. Обращение к строке этого файла позволяет восстановить значение k-го компонента производной от решения по схеме Горнера. Номер строки типизированного файла, соответственной произвольному значению независимой переменной 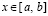 , является номером подынтервала, которому принадлежит x,
, является номером подынтервала, которому принадлежит x, 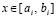 , и определяется из соотношения
, и определяется из соотношения 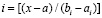 , или
, или
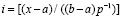 , (94)
, (94)
где [α] – целая часть числа α.
Предложение 5. Предложение 4 с точностью до обозначений повторяется для коэффициентов полинома 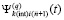 ,
,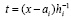 , приближающего k-й компонент решения задачи (89). Они имеют числовые значения,
, приближающего k-й компонент решения задачи (89). Они имеют числовые значения, 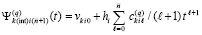 , по всем номерам подынтервалов из (90) образуют массив из p строк вида
, по всем номерам подынтервалов из (90) образуют массив из p строк вида 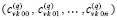 ,
, 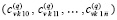 , …,
, …, 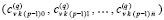 , который можно хранить в виде типизированного файла. Обращение к строке этого файла позволяет восстановить значение k-го компонента решения задачи (89) по схеме Горнера. Номер строки определяется из (94).
, который можно хранить в виде типизированного файла. Обращение к строке этого файла позволяет восстановить значение k-го компонента решения задачи (89) по схеме Горнера. Номер строки определяется из (94).
Результатом данных преобразований является линеаризованное приближение задачи (89), такое, что и решение, и правая часть системы (89) приближены с наперед заданной точностью. Компонент правой части на текущем подынтервале 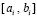 приближает полином
приближает полином 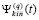 ,
, 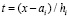 . Для задачи (89) полученное приближение рассматривается как частный случай линейной системы
. Для задачи (89) полученное приближение рассматривается как частный случай линейной системы 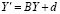 ,
, 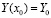 , где
, где 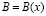 ,
, 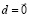 . Таким образом,
. Таким образом,
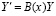 ,
, 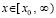 , (95)
, (95)
где k-я строка матрицы B(x) при 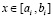 имеет вид
имеет вид 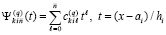 . При этом B(x) является диагональной матрицей
. При этом B(x) является диагональной матрицей
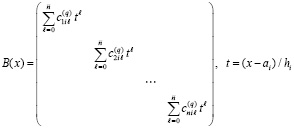 . (96)
. (96)
Для системы (95), (96) можно выполнить преобразования (78)–(80), (87), (88). В результате анализ устойчивости сведется к анализу системы вида (77) по схеме (79), где 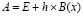 , шаг метода Эйлера
, шаг метода Эйлера 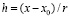 убывает к нулю на любом отрезке
убывает к нулю на любом отрезке 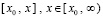 ,
, 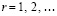 . С точностью до обозначений остается применить теорему 11 и соотношения (87), (88). Произведение матриц сведется к произведению диагональных элементов:
. С точностью до обозначений остается применить теорему 11 и соотношения (87), (88). Произведение матриц сведется к произведению диагональных элементов:
 (97)
(97)
Реальный контроль устойчивости сведется к контролю значения модуля накапливаемого произведения полиномов 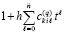 в процессе приближения каждого компонента с номером
в процессе приближения каждого компонента с номером 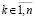 . Предварительно потребуется согласовать шаг метода Эйлера h и длину подынтервала
. Предварительно потребуется согласовать шаг метода Эйлера h и длину подынтервала 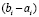 . Для численного моделирования устойчивости нулевого решения задачи (89) достаточно выбрать длинный конечный отрезок [a, b] из (90). Для аналитической оценки потребуется оценивать (97) в случае [a, b] произвольной длины.
. Для численного моделирования устойчивости нулевого решения задачи (89) достаточно выбрать длинный конечный отрезок [a, b] из (90). Для аналитической оценки потребуется оценивать (97) в случае [a, b] произвольной длины.
Кусочно-интерполяционное решение задачи (89) дает возможность компьютерной оценки устойчивости без перехода к линеаризации. Поскольку есть приближение решения 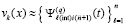 , то для каждого компонента с номером
, то для каждого компонента с номером 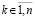 автоматически выводится
автоматически выводится 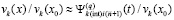 , t из (97), что влечет применение теоремы 1 и критериев (24), (25). Аналогичное приближение,
, t из (97), что влечет применение теоремы 1 и критериев (24), (25). Аналогичное приближение, 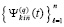 , есть для правой части (89), для каждого ее компонента получается
, есть для правой части (89), для каждого ее компонента получается 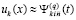 , что влечет возможность подстановки в (22), (23) и применения леммы 3. Кроме того, есть возможность воспользоваться теоремой 9 на основе подстановки в (70), (71) именно приближения
, что влечет возможность подстановки в (22), (23) и применения леммы 3. Кроме того, есть возможность воспользоваться теоремой 9 на основе подстановки в (70), (71) именно приближения 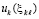 . Как отмечалось,
. Как отмечалось, 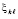 можно найти как минимум модуля левой части равенства (72). Подстановка приближений в (72) влечет
можно найти как минимум модуля левой части равенства (72). Подстановка приближений в (72) влечет
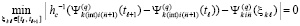 . (98)
. (98)
Решение уравнения (98) без принципиальных затруднений реализуется с помощью метода поиска корней полиномов, изложенного в [16]. При этом поиск выполняется именно как поиск минимума модуля полинома на отрезке. В этом случае в силу принципа минимума модуля никаких иных минимумов левой части (98) кроме корней полинома под знаком модуля не существует. Происходит автоматическая локализация корней 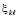 на промежутке
на промежутке 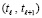 и их вычисление с высокой точностью. Процесс воспроизводится
и их вычисление с высокой точностью. Процесс воспроизводится 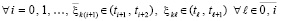 из (70), (71), что приводит к численной модели анализа устойчивости на основе теоремы 9.
из (70), (71), что приводит к численной модели анализа устойчивости на основе теоремы 9.
Примеры численного моделирования устойчивости. Нулевое решение системы
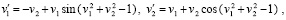 (99)
(99)
где 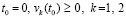 , асимптотически устойчиво. Это показывает программа (Delphi)
, асимптотически устойчиво. Это показывает программа (Delphi)
program RAE1111;
{$APPTYPE CONSOLE}
uses
SysUtils;
const h = 0.00001; tt=1000000;
var t,v1,v2,v10,v20,sum1,sum2: extended; k: longint;
function u1(t,v1,v2:extended):extended;
begin u1:=-v2+v1*sin((sqr(v1)+sqr(v2)-1)); end;
function u2(t,v1,v2:extended):extended;
begin u2:=v1+v2*cos((sqr(v1)+sqr(v2)-1)); end;
begin
k := 0; v10:=0.00005{*10}{/10}; v20:=0.00005{*10}{/10};
v1:=v10; v2:=v20; sum1:=0;sum2:=0;
t:=0; while t <=10000 do begin
v1:= v1+ h * u1(t,v1,v2); v2:= v2+ h * u2(t,v1 ,v2 );
sum1:=sum1+ u1(t,v1,v2); sum2:=sum2+ u2(t,v1,v2);
k:=k+1; if k = tt then begin writeln (‘t=’,t:2:20,’ ‘);
writeln (‘|v1/v10|=’,abs(v1/v10):2:20,’ ‘,’|v2/v20|=’,abs(v2/v20):2:20,’ ‘);
writeln (‘|u1/v10|=’,abs(u1(t,v1,v2)/v10):2:20,’ ‘,’|u2/v20|=’,abs(u2(t,v1 ,v2 )/v20):2:20,’ ‘);
writeln (‘|(h*sum1)/v10+1|=’,abs((h*sum1)/v10+1):2:20,’ ‘,’|(h*sum2)/v20+1|=’,abs((h*sum2)/v20+1):2:20,’ ‘);
writeln (‘|h*sum1+v10|=’,abs(h*sum1+v10{1}):2:20,’ ‘,’|h*sum2+v20|=’,abs(h*sum2+v20{1}):2:20,’ ‘);
k:=0 end; t:=t+h; end; readln
end.
Результат работы программы:
t=9.99998999999993814000
|v1/v10|=0.29125998463144390000 |v2/v20|=0.55060196113427734000
|u1/v10|=0.30551513518396883000 |u2/v20|=0.00623152503433619000
|(h*sum1)/v10+1|=0.29124462507297467000 |(h*sum2)/v20+1|=0.55059953302620732000
|h*sum1+v10|=0.00001456223125365000 |h*sum2+v20|=0.00002752997665131000
t=19.99998999999953070000
|v1/v10|=0.12474269340820399000 |v2/v20|=0.09358920299588803000
|u1/v10|=0.01137815406980509000 |u2/v20|=0.07417623122037619000
|(h*sum1)/v10+1|=0.12472416491684224000 |(h*sum2)/v20+1|=0.09358430563734230000
|h*sum1+v10|=0.00000623620824584000 |h*sum2+v20|=0.00000467921528187000
t=29.99998999999912320000
|v1/v10|=0.01801949566185700000 |v2/v20|=0.00282119559851540000
|u1/v10|=0.01798407835883173000 |u2/v20|=0.01954379414904189000
|(h*sum1)/v10+1|=0.01800090111125236000 |(h*sum2)/v20+1|=0.00282661386466787000
|h*sum1+v10|=0.00000090004505556000 |h*sum2+v20|=0.00000014133069323000
……………………………………………………………………………………………
|v1/v10|=0.00000000000000000000 |v2/v20|=0.00000000000000000000
|u1/v10|=0.00000000000000000000 |u2/v20|=0.00000000000000000000
|(h*sum1)/v10+1|=0.00001841470982673000 |(h*sum2)/v20+1|=0.00000540302317802000
|h*sum1+v10|=0.00000000092073549000 |h*sum2+v20|=0.00000000027015116000
Моделирование выполняется на отрезке 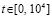 . Задача решается методом Эйлера с шагом h = 10–5. Данные выводятся с интервалом 101. На каждом интервале выводятся значения
. Задача решается методом Эйлера с шагом h = 10–5. Данные выводятся с интервалом 101. На каждом интервале выводятся значения 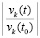 , k = 1, 2. Они ограничены значением 0.56 и убывают до 0. По теореме 1 согласно (24) это (предварительно) означает устойчивость нулевого решения. Ввиду соответствия (25) устойчивость асимптотическая. С таким же интервалом выводятся значения
, k = 1, 2. Они ограничены значением 0.56 и убывают до 0. По теореме 1 согласно (24) это (предварительно) означает устойчивость нулевого решения. Ввиду соответствия (25) устойчивость асимптотическая. С таким же интервалом выводятся значения 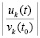 , k = 1, 2. Они ограничены значением 0.4 и убывают до 0. По теореме 7, где принято hc = h = 10–5, согласно (54) (предварительно) это означает устойчивость нулевого решения. То же, в соответствии (53), показывает вывод значений
, k = 1, 2. Они ограничены значением 0.4 и убывают до 0. По теореме 7, где принято hc = h = 10–5, согласно (54) (предварительно) это означает устойчивость нулевого решения. То же, в соответствии (53), показывает вывод значений 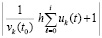 (в программе |(h*sum1)/v10+1|, |(h*sum2)/v20+1|).
(в программе |(h*sum1)/v10+1|, |(h*sum2)/v20+1|).
По теореме 8 (предварительно) ввиду соответствия (60), (61) устойчивость асимптотическая. Кроме того, с приближением 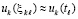 выводимые данные соответствуют (70) и (71), что по теореме 9 (предварительно) означает асимптотическую устойчивость нулевого решения задачи (99).
выводимые данные соответствуют (70) и (71), что по теореме 9 (предварительно) означает асимптотическую устойчивость нулевого решения задачи (99).
При варьировании начальных значений (закомментировано в программе) воспроизводятся аналогичные результаты, что окончательно подтверждает предварительно сделанные выводы.
Если теперь систему (99) заменить системой
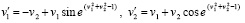 (100)
(100)
где 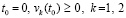 , то по той же программе с соответственным изменением
, то по той же программе с соответственным изменением
function u1(t,v1,v2:extended):extended;
begin u1:=-v2+v1* sin(exp((sqr(v1)+sqr(v2)-1))); end;
function u2(t,v1,v2:extended):extended;
begin u2:=v1+v2* cos(exp((sqr(v1)+sqr(v2)-1))); end;
получится
t=9.99998999999993814000
|v1/v10|=500.59684804253400900000 |v2/v20|=767.20968887111535100000
|u1/v10|=586.81541388098810600000 |u2/v20|=1216.26073371725572000000
|(h*sum1)/v10+1|=500.59097348477086600000 |(h*sum2)/v20+1|=767.21685432457260900000
|h*sum1+v10|=0.02502954867423854000 |h*sum2+v20|=0.03836084271622863000
t=19.99998999999953070000
|v1/v10|=25740.68140412086640000000 |v2/v20|=13022.59203072221274000000
|u1/v10|=8018.31786635432274000000 |u2/v20|=12966.55858312267237000000
|(h*sum1)/v10+1|=25740.60122734582730000000 |(h*sum2)/v20+1|=13022.72395324083090000000
|h*sum1+v10|=1.28703006136729137000 |h*sum2+v20|=0.65113619766204155000
t=29.99998999999912320000
|v1/v10|=13435.20336590923715000000 |v2/v20|=22388.86798987410960000000
|u1/v10|=10302.11110067168487000000 |u2/v20|=3659.19056796498126000000
|(h*sum1)/v10+1|=13435.10035120185532000000 |(h*sum2)/v20+1|=22388.71617758612430000000
|h*sum1+v10|=0.67175501756009277000 |h*sum2+v20|=1.11943580887930622000
…………………………………………………………………………………………..
t=9999.99998996787937000000
|v1/v10|=27329.70500137057080000000 |v2/v20|=9943.61504761500123000000
|u1/v10|=7388.24417752908457000000 |u2/v20|=17429.65163532512830000000
|(h*sum1)/v10+1|=27329.63112533244450000000 |(h*sum2)/v20+1|=9943.78624790049977000000
|h*sum1+v10|=1.36648155626662222000 |h*sum2+v20|=0.49718931239502499000
Выводимые данные возрастают, превосходя возможные ограничения (соответственно не обнаруживают стремления к нулю). При этом уменьшение начальных значений при повторных запусках программы влечет обратно пропорциональный рост значений выводимых данных. Это нарушает необходимое условие устойчивости теоремы 1, а также теоремы 9. Следовательно, нулевое решение задачи (100) неустойчиво.
Если теперь взамен (100) рассматривать систему
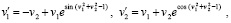 (101)
(101)
где 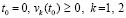 , то та же программа с соответственным изменением
, то та же программа с соответственным изменением
function u1(t,v1,v2:extended):extended;
begin u1:=-v2+v1* exp(sin((sqr(v1)+sqr(v2)-1))); end;
function u2(t,v1,v2:extended):extended;
begin u2:=v1+v2* exp(cos((sqr(v1)+sqr(v2)-1))); end;
даст следующие результаты:
t=9.99998999999993814000
|v1/v10|=77862.42446241906800000000 |v2/v20|=26314.83256975851240000000
|u1/v10|=91439.40445717954740000000 |u2/v20|=68024.75800006116810000000
|(h*sum1)/v10+1|=77863.33885077439920000000 |(h*sum2)/v20+1|=26314.95314129935520000000
|h*sum1+v10|=3.89316694253871996000 |h*sum2+v20|=1.31574765706496776000
t=19.99998999999953070000
|v1/v10|=3757708443.45288119000000000000 |v2/v20|=945857167.41732183100000000000
|u1/v10|=885366228.63872246800000000000 |u2/v20|=5653293084.85314156000000000000
|(h*sum1)/v10+1|=3757717297.11517323000000000000 |(h*sum2)/v20+1|=948270838.40854998000000000000
|h*sum1+v10|=187885.86485575866100000000 |h*sum2+v20|=47413.54192042749900000000
t=29.99998999999912320000
|v1/v10|=444655451909496.94400000000000000000 |v2/v20|=476839954039750.91100000000000000000
|u1/v10|=32184502130253.96730000000000000000 |u2/v20|=921495405949247.85500000000000000000
|(h*sum1)/v10+1|=444655130064475.63900000000000000000 |(h*sum2)/v20+1|=476735427207564.45800000000000000000
|h*sum1+v10|=22232756503.22378200000000000000 |h*sum2+v20|=23836771360.37822290000000000000
……………………………………………………………………………………………………………....
Далее наступит переполнение. При варьировании начальных значений результаты аналогичны. Согласно теоремам 1 и 9 нулевое решение задачи (101) неустойчиво.
Изложенный способ компьютерного анализа устойчивости дает пошаговую информацию по ходу решения и может применяться в режиме реального времени. Если вычисление значений 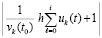 замедляет процесс, то можно отменить их вычисление и оценивать устойчивость по поведению
замедляет процесс, то можно отменить их вычисление и оценивать устойчивость по поведению 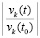 на основе теоремы 1, правда, оценка на основе теорем 8, 9 достоверна в условиях непрерывности правой части в R0 без требования ее дифференцируемости.
на основе теоремы 1, правда, оценка на основе теорем 8, 9 достоверна в условиях непрерывности правой части в R0 без требования ее дифференцируемости.
Представленные результаты следующим образом сравниваются с известными. Необходимые и достаточные условия устойчивости теоремы 1, леммы 3, теоремы 9 сохраняют отличие от условий устойчивости традиционных методов [1, 2], а также [3, 4], представляющих, как правило, достаточные условия устойчивости. В отличие от предложенных, эти методы не предоставляют возможности численного моделирования устойчивости. Подходы, опирающиеся на компьютерные технологии, в частности [5–10], а также [10, 11], аналогично не используют численные методы решения ОДУ, в то время как их применение приводит к изложенным выше условиям устойчивости и позволяет выполнять численное моделирование устойчивости по ходу решения задачи в реальном времени. Аналогичные отличия можно привести относительно теорем 10, 11, применимых к линейным системам. Дополнительно можно отметить, что, в отличие от известных подходов, условия (85)–(88) не требуют информации, как-либо связанной с характеристическим полиномом матрицы коэффициентов, а также с характеристическими показателями [1].
Заключение
Предложены необходимые и достаточные условия устойчивости в смысле Ляпунова решений ОДУ общего вида, указаны границы их применимости. Аналитические оценки устойчивости исходят непосредственно из компонентов правой части дифференциальной системы, без их преобразований, без применения функции Ляпунова. Численные оценки устойчивости опираются на приближенное решение системы ОДУ и дают возможность анализа устойчивости по ходу компьютерной реализации численного интегрирования. Дано математическое обоснование предложенных критериев, их практическое применение и достоверность иллюстрируются результатами численного эксперимента.
Библиографическая ссылка
Ромм Я.Е. ОБ УСЛОВИЯХ УСТОЙЧИВОСТИ С ОБРАТНОЙ ПРОПОРЦИЕЙ НАЧАЛЬНЫМ ЗНАЧЕНИЯМ РЕШЕНИЙ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ // Современные наукоемкие технологии. 2023. № 9. С. 31-60;URL: https://top-technologies.ru/ru/article/view?id=39760 (дата обращения: 21.12.2025).
DOI: https://doi.org/10.17513/snt.39760



