Продукция, сырье химических производств могут быть пылящими, ядовитыми, токсичными, обладать мутагенными и канцерогенными свойствами. Этими свойствами продукции и сырья обусловлено обилие участков с вредными или особо опасными условиями труда [1].
Отметим, что наличие в производственной среде мутагенных и канцерогенных соединений указывает на необходимость систематического мониторинга загрязнений, гигиенической оценки рабочих мест. Это определяет необходимость использования в химических производствах коллектива роботов-лаборантов производящих определенные виды работ на разных аппаратах в различное время.
Невозможность ошибок в работе коллектива роботов-лаборантов, тяжелейшие последствия таких ошибок требуют разработки принципиально новых алгоритмов управления роботами-лаборантами, учитывающих возможность случайных помех и гарантирующих выполнение технологических и технических требований с вероятностью не ниже заданной [2].
При управлении коллективом роботов-лаборантов (РЛ) в робототехнических автоматизированных системах управления (РоАСУ) должно приниматься решение о распределении работ среди РЛ, о времени, выделяемом конкретным РЛ на обслуживание тех или иных технологических объектов. При этом эффект от распределения РЛ обычно пропорционален времени, выделяемому роботам на выполнение той или иной работы. Так, частота взятия на лабораторный анализ проб в АСУТП позволяет чаще корректировать программу управления, увеличивая при этом экономический эффект. Частота отбора проб в определенном месте, например, химико-технологического процесса повышает их аварийную и экологическую безопасность. При этом увеличение эффективности технологических процессов в зависимости от частоты взятия проб различно для различных процессов. Учитывая ограниченность ресурсов времени работы РЛ, встает задача оптимизации времени загрузки РЛ. Эта задача в ограниченном диапазоне вариации времени загрузки РЛ может трактоваться как задача линейного программирования [2–4].
При допустимости существенной вариации времени загрузки РЛ скорость прироста экономического эффекта при увеличении частоты проб уменьшается. Действительно, при достаточно большой частоте отбора проб дальнейшее увеличение этой частоты сказывается незначительно. Таким образом, при больших областях вариации времени загрузки РЛ имеет место нелинейная зависимость целевой функции (эффективность технологического процесса) от увеличения частоты отбора проб. В этом случае, очевидно, задачи оптимизации времени загрузки РЛ относятся к классу нелинейных задач оптимизации.
Наличие возмущающих воздействий и случайного характера протекания технологического процесса (например, неидеальности смешения реакционных смесей, наличия застойных зон) делают качественные характеристики технологического процесса случайными. При этом нельзя считать детерминированной и постановку задачи управления коллективами РЛ. При этом целевая функция и технологические ограничения являются, очевидно, случайными величинами. Однако в РоАСУ все технологические ограничения должны быть выполнены с вероятностью не ниже заданной. Таким образом, необходимо рассматривать при управлении коллективом РЛ следующую задачу, которую будем в дальнейшем называть задачей надежного оптимального управления [5].
Необходимо определить вектор u* ∈ U , при котором принимает минимальное значение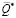 
математическое ожидание целевой функции:
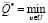M[Q(u)]. (1)
и вероятность Р выполнения технологических ограничений
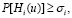
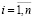(2)
превосходит некоторое заданное значение σi,
где М – математическое ожидание случайной целевой функции Q;
U – множество допустимых значений вектора управления u;
Hi(u) – i-е технологическое ограничение;
n – число технологических ограничений;
σi – константа.
Цель исследования заключается в разработке теоретических положений планирования работы коллектива роботов-лаборантов в условиях неопределенности.
Материалы и методы исследования
Рассмотрим постановку и решение задачи надежного линейного программирования с суммарной случайной величиной.
Пусть линейная целевая функция имеет суммарную величину V:
Q(u) = Cu + V, (3)
где С = (с1, …,сn ), u = (u1,…,un ).
Пусть технологические ограничения имеют аналогичную форму:
biu + Vi ≥ ai, (4)
где bi = (bi1,…,b1n).
Будем считать известными плотности распределения ω(V) и ω(Vi) случайных величин V и Vi.
В соответствии с (1) и (2) сформулируем следующую задачу надежного управления.
Необходимо найти вектор u* ∈ U, при котором принимает минимальное значение математическое ожидание функции (3):
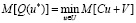(5)
и вероятность выполнения условий (4) не ниже заданных:
P[biu + Vi ≥ ai] ≥ σi, (6)
где σi – заданное значение вероятности выполнения i-го условия (4) и
ui ≥ 0. (7)
Задачу (5)–(6) будем называть задачей надежного линейного программирования с суммарной случайной величиной.
Учитывая линейность целевой функции (3) задача (5)–(7) может быть переформулирована в следующем виде.
Необходимо найти вектор u* ∈ U, при котором принимает минимальное значение целевая функция:
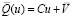, (8)
где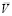 
– математическое ожидание случайной величины V:
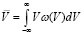, (9)
и удовлетворении ограничений
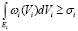. (10)
Ei = (Vi | biu + Vi ≥ ai). (11)
Будем называть эквивалентной задачей следующую задачу линейного программирования.
Найти n-мерный вектор u, при котором принимает минимальное значение целевая функция:
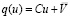(12)
И удовлетворяются ограничения
biu ≥ αi (13)
u ≥ 0, (14)
где
αi = ai – ti, (15)
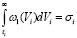(16)
Теорема 1. Задача надежного линейного программирования с суммируемой случайной величиной (8)–(11) тождественная эквивалентной задаче линейного программирования (12)–(16).
Доказательство. Так как целевые функции задач (3)–(11) и (12)–(16) совпадают, для доказательства тождественности этих задач необходимо и достаточно доказать тождественность условия (10), где Ei определяется (11), условию (13), где αi определяется (15)–(16).
Для доказательства введем параметр ti, определяемый условием
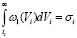. (17)
Выразим технологическое неравенство (4), участвующее в определении (11) Ei в виде
Vi ≥ ai – biu
При этом условие (10)–(11) может быть переписано в виде
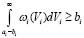. (18)
Сравнение (17), (18) показывает, что условие (10), (11) выполняется, если
ai – biu ≤ ti. (19)
Действительно, в этом случае
.
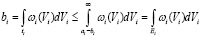Используя (19), имеем
biu = ai – ti (20)
или biu ≥ αi, где αi = ai – ti.
Теорема 1 доказана.
Таким образом, задача надежного линейного программирования с суммарной случайной величиной свелась к традиционной детерминированной задаче линейного программирования (12)–(14), где в технологических ограничениях вместо ai используется αi, определенное по (15). При этом величина ti должна быть предварительно найдена из соотношения (16).
Далее рассмотрим задачу надежного линейного программирования с мультипликативным вхождением случайной величины.
Рассмотрим задачу оптимизации, в которой целевая функция имеет вид
Q(u) = VCu, (21)
а технологические ограничения могут быть представлены в виде
Vibiu ≥ ai. (22)
где вектора C, b, u, а случайные величины V, Vi определяются так же, как в предыдущей задаче.
В соответствии с (1)–(2) сформулируем задачу надежного управления.
Необходимо найти вектор u* ∈ U, при котором принимает минимальное значение математическое ожидание функции (21):
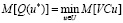(23)
и вероятности выполнения условий (22) не ниже заданных значений σi:
P[Vibiu ≥ ai] ≥ σi, (24)
ui ≥ 0. (25)
Учитывая линейность целевой функции (21), задача (23)–(25) может быть переформулирована в следующем виде.
Необходимо найти вектор u* ∈ U, при котором принимает минимальное значение целевая функция:
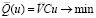, (26)
где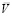 
– математическое ожидание случайной величины V, определяемой (9), и удовлетворяются ограничения
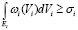, (27)
где
Ei = (Vi | Vibiu ≥ ai). (28)
ui ≥ 0. (29)
Будем называть эквивалентной задачей следующую задачу линейного программирования.
Найти n-мерный вектор u, при котором принимает минимальное значение целевая функция:
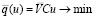(30)
и удовлетворяются ограничения
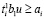, (31)
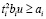(32)
u ≥ 0, (33)
где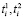 
определяются из соотношений
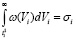, (34)
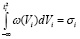(35)
Теорема 2. Задача надежного линейного программирования с мультипликативным вхождением случайной величины (26)–(29) тождественна эквивалентной задаче (31)–(35).
Доказательство. Так как целевые функции задач (26)–(29) и (31)–(35) совпадают, то для доказательства тождественности этих задач достаточно доказать тождественность условий (27), где Ei определяется (28) и (31)–(32). Пусть параметры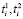 
определяются соотношениями (34)–(35).
Технологическое неравенство (22) может быть, очевидно, записано в виде системы неравенств
vi ≥ ai / biu, если biu ≥ 0,
vi ≤ ai / biu, если biu < 0.
При этом (28) может быть переписано в следующем тождественном виде:
Ei = (vi | vi ≥ ai / biu), если biu ≥ 0,
и vi ≤ ai / biu, если biu < 0). (36)
С использованием (36) условие (27) может быть записано в следующей тождественной форме:
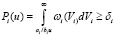,если biu ≥ 0 (37)
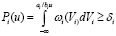, если biu < 0, (38)
где Pi(u) – обозначение вероятности i-го условия.
Сравнение (34) c (37) показывает, что условие (27)–(28) будет выполнено для biu ≥ 0, если
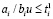. (39)
Доказательство в этом случае
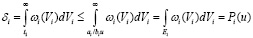. (40)
Аналогично, сравнение (35) с (38) показывает, что при biu условие (27)–(28) будет выполнено, если
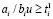. (41)
Действительно, при этом имеет место
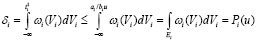. (42)
Таким образом, из (40), (42) с учетом (39) и (41) следует, что условия (27)–(28) выполняются, если в эквивалентной задаче выполняются системы неравенств
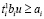, biu ≥ 0 (43)
или
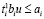, biu ≥ 0 (44)
Теорема 2 доказана.
Таким образом, задача надежного линейного программирования в мульпликативном вхождении случайной величины свелась к детерминированной задаче линейного программирования вида (30)–(35), в которой использованы вдвое большие технологические ограничения (31), (32), нежели в первоначальной задаче. При этом в определении (31), (32) параметры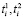 
являются константами, определяемыми из (34) и (35).
Заключение
Рассмотренные теоретические положения позволяют планировать работу коллектива роботов-лаборантов, обеспечивая требуемую вероятность выполнения объемов работ технических и технологических условий. Однако в РоАСУ все технологические ограничения должны быть выполнены с вероятностью не ниже заданной. Таким образом, необходимо рассматривать и решать при управлении коллективом роботов-лаборантов задачи надежного оптимального управления. Результаты, полученные в данном исследовании, подтверждают результаты исследований технологического процесса производства азопигментов.
Библиографическая ссылка
Калинин В.Ф., Погонин В.А. ПЛАНИРОВАНИЕ РАБОТЫ КОЛЛЕКТИВА РОБОТОВ-ЛАБОРАНТОВ // Современные наукоемкие технологии. – 2023. – № 9. – С. 20-24;URL: https://top-technologies.ru/ru/article/view?id=39758 (дата обращения: 21.11.2024).