Системы передачи данных OFDM постоянно расширяют области своего применения. Благодаря своим достоинствам технология OFDM нашла применение и в системе спутникового интернета StarLink, построенного на основе низкоорбитальных спутников [1]. В ряде работ [2, 3] рассмотрен способ увеличения скорости передачи данных в OFDM за счет перехода от быстрых преобразований Фурье (БПФ) к дискретным вейвлет-преобразованиям (ДВП), так как это позволяет уменьшить уровень боковых лепестков спектра OFDM сигнала. В результате этого можно поместить большее число каналов OFDM в заданной полосе частот. Дальнейшее повышение эффективности систем OFDM связано с использованием конечных полей Галуа GF(M) [4] и модулярных кодов класса вычетов (МККВ) [5]. Применение данных алгебраических систем обеспечивает повышение скорости цифровой обработки сигналов на основе вычислений целочисленного ДВП (ЦДВП). Использование данных моделей реализации целочисленных преобразований в полях GF(M) и МККВ окажет значительное влияние на структуру систем OFDM. Поэтому разработка структурных моделей системы передачи OFDM, использующих ЦДВП Добеши в GF(M) и модулярных кодах, является актуальной задачей. Цель статьи – осуществить разработку структурных моделей систем OFDM, применяющих ЦДВМ Добеши в GF(M) и МККВ. При этом использование таких моделей должно привести к увеличению скорости передачи данных.
Материалы и методы исследования
По мере расширения требований, которые предъявляются к скорости передачи данных в беспроводных сетях, увеличивается число телекоммуникационных систем, использующих технологию, в основу которой положено ортогональное частотное мультиплексирование. Технология OFDM построена на идее, согласно которой высокоскоростной поток информации разбивается на множество более низкоскоростных потоков. При этом для оказания минимального воздействия одного низкоскоростного потока на другой в системах OFDM предлагается использовать БПФ и обратное БПФ. Для снижения негативного влияния многолучевости при распространении радиосигнала в системах OFDM используется циклический префикс. Прежде чем перейдем к разработке структурной модели системы OFDM, использующей ЦДВП Добеши в МККВ, рассмотрим принципы построения кодов классов вычетов.
1.1. Модулярные коды классов вычетов
Для генерации кодовых комбинаций в МККВ используются основания – числа pi, i = 1,2,…,k, которые имеют наибольший общий делитель НОД(pi, pj) = 1, при условии i ≠ j. Их произведение задает множество возможных комбинаций и называется диапазоном
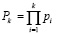. (1)
Тогда кодовая комбинация МККВ имеет вид [6–8]
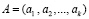, (2)
где А – целое число; A < Pk,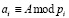
; i = 1,2,…,k.
Так как МККВ обладают свойством кольца, то для модульных операций справедливо
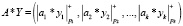, (3)
где * – операции сложения, вычитания и умножения;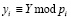 
; Y < Pn; i = 1,2,…,k.
Очевидно, что при выполнении модульных операций МККВ распараллеливают их. А так как остатки имеют маленькую разрядность, то вместо сумматоров и умножителей по модулю можно взять LUT-таблицы. Все это позволит сократить время вычислений. Однако при использовании МККВ необходимы еще две обязательные немодульные операции. Так как они приводят к увеличению времени вычислений, то необходимо выбрать такие алгоритмы их выполнения, чтобы уменьшить это влияние. Первая немодульная операция связана переводом позиционного кода, представленного в позиционной системе счисления (ПСС) в МККВ. В настоящее время широко используются алгоритмы прямого перевода на основе распределенных вычислений [6]. В этом случае позиционный код разбивается на L блоков по С разрядов. Затем вычисляются остатки данных блоков:
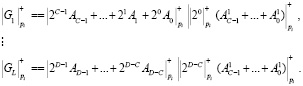(4)
Тогда для получения остатка необходимо выполнить выражение
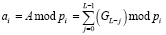, i = 1,2,…,k. (5)
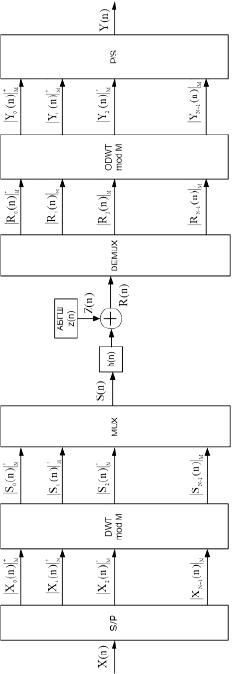
Рис. 1. Структурная модель OFDM, построенная на основе выполнения ЦДВП в GF(M)
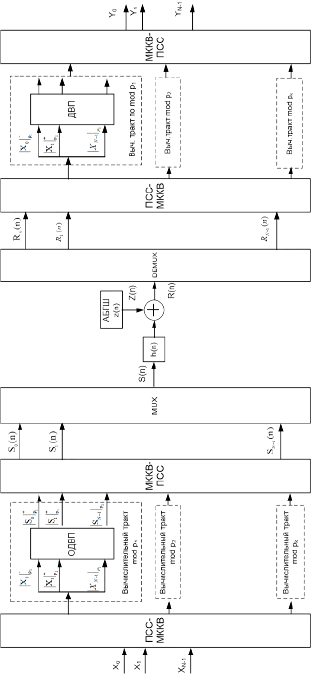
Рис. 2. Структурная модель системы OFDM, использующей ЦДВП Добеши в МККВ
При выполнении второй немодульной операции осуществляется перевод из МККВ в ПСС. Как правило, для этого используется Китайская теорема об остатках (КТО) [7, 8]. Для этого вычисляют ортогональные базисы:
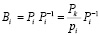, (6)
где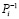 
– вес ортогонального базиса, чтобы обеспечить 
.
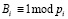Тогда обратный перевод выполняется
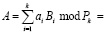
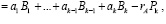(7)
где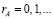 
– ранг числа.
Недостатком данного алгоритма обратного перевода в ПК является необходимость вычисления ранга числа. Данный недостаток можно устранить, если использовать следующий алгоритм. На первом этапе алгоритма вычисляются выражения, где i = 1,2,…,k,
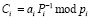. (8)
На втором этапе полученные результаты умножаются на константы Pi, где i = 1,2,…,k,
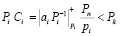. (9)
На третьем этапе находится попарная сумма первых двух произведений. Затем осуществляется сравнение с рабочим диапазоном. Если сумма больше, то из нее вычитается рабочий диапазон. Данные действия повторяются в течение k – 1 этапов. Именно данный алгоритм обратного преобразования и алгоритм распределенной арифметики будут использованы в реализации на основе ПЛИС.
1.2. Разработка структурных моделей систем OFDM, построенных на основе ЦДВП Добеши, использующих целочисленные системы
При разработке структурной модели системы OFDM был использован материал, представленный в [4]. На основе данного материала была создана структурная модель системы OFDM, построенная на основе выполнения ЦДВП в конечных полях, которая представлена на рис. 1.
При реализации структурной модели выполнения ДВП Добеши в МККВ был использован источник [5]. Данная модель показана на рис. 2.
Рассмотрим передающую сторону системы. Для организации передачи поток данных Х делится на N блоков. Получаем вектор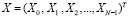 
. Длина каждого блока составляет М разрядов и определяется из условия
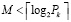. (10)
Блоки полученного входного вектора поступают на входы соответствующего преобразователя ПСС-МККВ. Так, с выхода с первого преобразователя ПСС-МККВ будет снят модулярный код
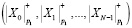, (11)
где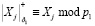 
; j = 0,1,…,N–1.
Полученные кодовые комбинации поступают на входы соответствующего вычислительного тракта по модулю pi, где i = 1,…,n. Вычислительные тракты реализуют обратное ЦДВП (ОЦДВП) в МККВ. В этом случае входные блоки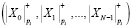 
представляются как кортеж аппроксимирующих 
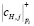и детализирующих 
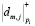коэффициентов, которые были получены на высшем уровне разложения H. Очевидно, что данные коэффициенты также представлены в МККВ, где 
; 
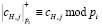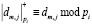; m = 1,…,H. В этом случае часть входных блоков 
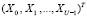, представленных в МККВ, являются аппроксимирующими коэффициентами. Вторая половина входных блоков 
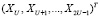, представленная в МККВ, является детализирующими коэффициентами наивысшего уровня dM,j. Оставшиеся входные блоки 
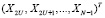представляют собой детализирующие коэффициенты dm,n, где m = 1,…,H.
В каждый вычислительный тракт по модулю входят блоки цифровых фильтров, которые реализуют ОДВП в МККВ (на схеме они показаны блоками ОДВП). Коэффициенты цифровых фильтров подобраны таким образом, чтобы выполнилось обратное ЦДВП
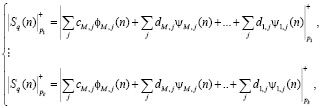(12)
где cH,j – аппроксимирующие коэффициенты на уровне разложения Н; dm,j – коэффициенты детализации; m = 1,…,H; φM,j – скейлинг функция; ψm,j – вейвлет-функция; j = 0,1,…,2j–1 – диапазоны сдвига;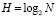 
– число уровней разложения; q = 0,1,…,N–1.
Результаты выполнения выражения (12), которые представляют собой модулярные комбинации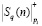 
отсчетов сигналов, подаются на входы преобразователя МККВ-ПСС. С помощью такого преобразователя вычисляется
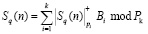, (13)
где q = 0,1,…,N–1.
Вычисленные значения
,
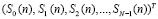представленные в коде ПСС, поступают на входы мультиплексора (MUX). Он осуществляет объединение всех N блоков в единый сигнал S(n). Затем сигнал S(n) с выхода передатчика поступает в дискретный канал связи h(n). В модели выбран дискретный канал с шумом, в качестве которого был выбран аддитивный белый гауссовский шум (АБГШ) Z(n). Наличие шума в канале связи приводит к появлению ошибок в передаваемом сигнале. Пусть Z(n) обладает нулевым средним и дисперсией, равной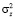 
. Пусть в разработанной структурной модели системы передачи данных обеспечена идеальная синхронизация. В результате на входе приемника системы OFDM поступает сигнал
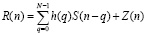. (14)
Затем сигнал R(n) поступает на вход демультиплексора (DEMUX). Он делит последовательный сигнал на N блоков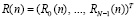 
, которые преобразуются в МККВ с помощью преобразователя ПСС-МККВ при q = 0,1,…,N–1.
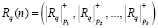. (15)
Данные значения поступают на входы k вычислительных трактов, которые выполняют прямое ЦДВП по модулю
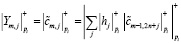,(16)
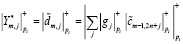.(17)
где Ym,j = cm,j – аппроксимирующие коэффициенты ДВП, соответствующие уровню m;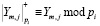 
; 
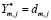– детализирующие коэффициенты ДВП, соответствующие уровню m; m = 1,…,H; 
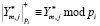; где hj, gj – коэффициенты НЧ-фильтра и ВЧ-фильтра; 
; 
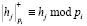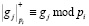; i = 1,2,…,k.
Результаты вычислений, представленные в МККВ, поступают на входы преобразователя из МККВ-ПСС. На выходе данного преобразователя генерируется выходной сигнал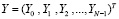 
.
Результаты исследования и их обсуждение
Разработанные структурные модели системы передачи OFDM, использующие целочисленные дискретные вейвлет-преобразования (ЦДВП) Добеши в GF(M) и МККВ, были реализованы на ПЛИС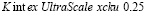 
.
Преобразования ПСС-МККВ и МКВ-ПСС реализованы согласно (7) и (10). В результате временные затраты на передающей стороне классической 8-разрядной системы OFDM составили 485 нс. При использовании разработанной структурной модели системы OFDM на основе ЦДВП в конечном поле при М=262147 – 241 нс, а при применении МККВ – 183 нс, что в 2,650 раза меньше, чем в системах, использующих БПФ. Таким образом, использование представленных в статье структурных моделей системы OFDM Добеши в конечных полях и МККВ позволяет за счет сокращения временных затрат на цифровую обработку сигналов повысить скорость передачи данных.
Заключение
В статье представлены структурные модели системы передачи OFDM, использующей ЦДВП Добеши в GF(M) и МККВ. Рассмотрены принципы работы данной модели. Проведена реализация структурных моделей с использованием ПЛИС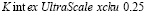 
.
Разработанные структурные модели имели меньшие временные затраты по сравнению с БПФ. Значит, использование этих моделей системы OFDM за счет сокращения временных затрат на цифровую обработку сигналов позволит повысить скорость передачи данных
Библиографическая ссылка
Чистоусов Н.К., Калмыков И.А., Духовный Д.В. РАЗРАБОТКА СТРУКТУРНЫХ МОДЕЛЕЙ СИСТЕМЫ OFDM, ИСПОЛЬЗУЮЩИХ ПРЕОБРАЗОВАНИЯ ДОБЕШИ В GF(M) И КОДАХ КЛАССОВ ВЫЧЕТОВ // Современные наукоемкие технологии. – 2023. – № 8. – С. 84-90;URL: https://top-technologies.ru/ru/article/view?id=39735 (дата обращения: 19.05.2024).