Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ким Д.Б. 1 Афанасьев Н.Т. 2 ТанаевА.Б. 2 Чудаев С.О. 2

---

1 ФГБОУ ВО «Братский государственный университет»

2 ФГБОУ ВО «Иркутский государственный университет»

Развит метод оперативной диагностики возможных статистических характеристик сигнала в информационном канале с трехмерными флуктуациями параметров по данным измерений флуктуационных характеристик пробного сигнала. С помощью метода возмущений получены алгебраические уравнения связи дисперсий направления распространения, доплеровского смещения частоты, групповой и фазовой задержки основного и пробного сигналов в информационном канале. Уравнения получены для фиксированных координат пунктов излучения и приема сигналов. Коэффициенты уравнений учитывают фундаментальные решения краевых задач Дирихле для основного и пробного сигналов. Интегралы для коэффициентов сведены к линейным дифференциальным уравнениям первого порядка с начальными условиями Коши. Сделан вывод общей системы дифференциальных уравнений для совместного расчета коэффициентов алгебраических уравнений и траекторных характеристик основного и пробного сигналов в регулярном канале. В качестве модели неопределенности параметров канала использована пространственно-временная корреляционная функция, учитывающая динамику средней диэлектрической проницаемости канала. Временные флуктуации параметров канала рассмотрены в приближении вмороженного переноса относительно направления распространения сигнала. Разработанный метод позволяет проводить экспресс-оценку возможных флуктуаций сигнала в информационном канале с неопределенностью параметров как в режиме просвечивания, так и в условиях отражения. Приведены примеры численных экспериментов для определения ожидаемых флуктуаций траекторных характеристик сигналов связи на различных рабочих частотах по данным измерений статистических характеристик сигнала пробного источника. Работа выполнена при финансовой поддержке Минобрнауки РФ (проекты FZZE-2020-0024, FZZE-2023-0004), с использованием УНУ «Астрофизический комплекс МГУ – ИГУ» (договор ЕВ-075-15-2021-675).

Статья в формате PDF

366 KB

информационный канал

сигналы

флуктуации

асимптотические разложения

алгоритмы

математическое моделирование

статистические характеристики

оптимизация

Долуханов М.П. Оптимальные методы передачи сигналов по линиям радиосвязи. 2-е изд. URSS. 2021. 176 с.

Липкин И.А. Статистическая радиотехника. Теория информации и кодирования. М.: Вузовская книга, 2017. 214 с.

Агеева Е.Т., Афанасьев Н.Т., Багинов А.В., Ким Д.Б., Танаев А.Б., Чудаев С.О. Диагностика состояния информационного канала по статистическим траекторным характеристикам реперного сигнала // Современные наукоемкие технологии. 2020. № 5. С. 9–14.

Kravtsov Yu.A., Orlov Yu.I. Geometrical Optics of Inhomogeneous Medium. Berlin: Springer-Verlag, 1990. 312 p.

Арнольд В.И. Математические методы классической механики. 6-е изд. URSS. 2017. 416 с.

Исимару А. Распространение и рассеяние волн в случайно неоднородных средах. Ч. 2. М.: Мир, 1981. 320 с.

Агеева Е.Т., Афанасьев Н.Т., Ким Д.Б., Чудаев С.О. Оперативные алгоритмы расчета характеристик лучевых полей в стохастических неоднородных средах // Современные наукоемкие технологии. 2019. № 2. С. 9–14.

Как известно [1, c. 9; 2, с. 138], для выбора частотно-углового режима передающих устройств и прогнозирования возможных флуктуаций характеристик сигналов в каналах передачи информации необходима априорная оценка состояния канала. Поскольку параметры реальных каналов известны лишь с определенной долей вероятности, оценка ожидаемых характеристик сигналов не всегда удовлетворяет потребности практики. Один из способов повышения качества и надежности передачи сигналов заключается в решении обратной задачи восстановления параметров канала по данным измерений характеристик некоторого пробного сигнала с дальнейшим использованием этих сведений в решении основной задачи передачи сигналов в заданном направлении. Кроме того, существует возможность так называемой прямой диагностики канала, когда ожидаемые характеристики передаваемых сигналов определяются непосредственно по данным измерений сигнала от некоторого пробного источника. В работе [3] нами был предложен подход для оценки некоторых статистических характеристик сигнала в информационном канале с двумерными флуктуациями параметров по флуктуациям сигнала пробного источника на фиксированной рабочей частоте. В настоящей работе этот подход использован в многочастотном режиме и применен для оценки комплекса статистических траекторных характеристик сигналов в канале с трехмерными флуктуациями параметров.

Цель работы заключается в развитии метода оперативной многочастотной диагностики возможных флуктуаций траекторных характеристик сигналов в информационном канале с трехмерной неопределенностью параметров по данным измерений флуктуаций встречного сигнала пробного источника.

Вывод функциональных связей

Для расчета статистических характеристик сигнала в информационном канале с неопределенностью параметров использовался метод геометрической оптики [4, с. 96]. В отличие от [3] траектории лучей определялись в трехмерном пространстве путем решения лучевых дифференциальных уравнений в форме Эйлера:

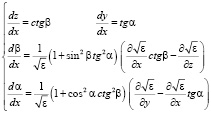, (1)

где x, y, z – переменные лучевые координаты; α, β – угловые параметры луча в горизонтальной и вертикальной плоскостях, ε – диэлектрическая проницаемость стохастического информационного канала, dx – элемент дальности.

Система уравнений (1) была решена методом возмущений [5, с. 234]. Диэлектрическая проницаемость канала задавалась суммой средней составляющей ⟨ε⟩ = ε0(z) и флуктуационной ε1(x,y,z). Предполагалось, что |ε1| << ε0, ⟨ε1⟩ = 0. Уравнения (1) были решены с помощью разложений:

β = β0 + β1, z = z0 + z1, α = α0 + α1, y = y0 + y1.

где β0 = ⟨β⟩, z0 = ⟨z⟩, α0 = ⟨α⟩, y0 = ⟨y⟩ – параметры средней траектории; β1, z1, α1, y1 – малые флуктуации траекторных параметров. Используя эти разложения и полагая, что средняя траектория лежит в плоскости Z0X (y0 = 0, α0 = 0), был сделан вывод уравнений для расчета средней траектории и ее флуктуаций.

Для построения статистических моментов характеристик сигнала рассматривались условия медленной динамики неопределенности параметров канала. В задаче определения возможных флуктуаций характеристик сигнала по измеренным флуктуациям пробного сигнала мы использовали упрощенную модель пространственно-временной корреляционной функции неопределенности параметров канала [6, с. 86]: N = N1N0, где N0 – гауссова корреляционная функция, множитель N1 описывает медленную пространственную динамику хаотических параметров канала. Функция N1 задавалась в виде 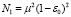, где μ2 – интенсивность неопределенности параметров канала. Временная динамика параметров канала учитывалась в приближении вмороженного переноса [6, с. 9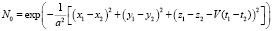2]:

, (2)

где t1, t2 – последовательные моменты времени, a – радиус пространственной корреляции неопределенности параметров канала, V – скорость вмороженного переноса относительно направления распространения сигнала.

Следуя подходу, предложенному в [3], неизвестные параметры корреляционной функции неопределенности параметров канала предварительно определялись по трем статистическим моментам пробного сигнала: дисперсиям доплеровского смещения частоты, групповой и фазовой задержек, а затем использовались для расчета возможных флуктуаций характеристик основного сигнала. Следует заметить, что структура приближенного решения для статистических моментов траекторных характеристик сигнала и выбранная модель пространственно-временной корреляционной функции неопределенности параметров канала позволяют по трем восстановленным параметрам модели рассчитать пять ожидаемых статистических характеристик основного сигнала в информационном канале. С учетом фиксированных координат приемных и передающих пунктов основных и пробного сигналов были получены алгебраические уравнения связи дисперсий флуктуационных характеристик этих сигналов в информационном канале:

,

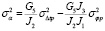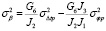
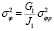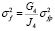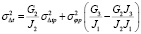, , , (3)

где 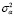, , 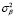, , 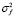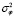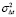– дисперсии горизонтального и вертикального углов прихода, доплеровского смещения частоты, фазы и групповой задержки основного сигнала; 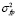, , 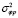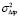– дисперсии доплеровского сдвига частоты, фазы и групповой задержки пробного сигнала; коэффициенты J1, J2, J3, J4, G1, G2, G3, G4, G5, G6 определяются из системы дифференциальных уравнений:

(4)

Здесь f – рабочая частота сигнала; xк, zк, z0(x), β0(x), βn – координаты приемного пункта и траекторные характеристики основного сигнала соответственно; xp , zp , z0p(x), β0p(x), βp – координаты пункта излучения и траекторные характеристики пробного сигнала; 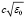– средняя составляющая групповой скорости сигнала; F(x) = F1(x) + F2(x), Fp(x) = F1p(x) + F2p(x),

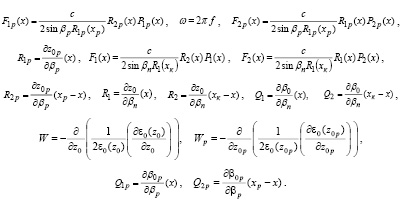
Краевые условия для системы (4):

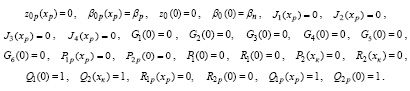(5)

Решение системы (4) намного проще решения исходных краевых стохастических задач для характеристик основного и пробного сигналов на фиксированных рабочих частотах, поскольку уравнения для J1, J2, J3, J4, G1, G2, G3, G4, G5, G6 интегрируются с начальными условиями. Последнее в значительной степени повышает производительность расчетов [7]. При многочастотном режиме работы в стохастическом канале дополнительно требуется пристрелка средних траекторий основных и пробного сигналов для каждой рабочей частоты, что легко достигается методами вычислительной математики.

Численные эксперименты

Предложенный метод позволяет проводить диагностику возможных флуктуаций характеристик сигналов в информационном канале как в режиме просвечивания, так и в условиях отражения. Для обоих этих режимов были поставлены численные эксперименты.

Регулярная диэлектрическая проницаемость канала с просвечиванием была задана двухслойной аналитической моделью:

, (6)

где fкрЕ, fкр, ymE, ym, zmE, zm – критические частоты, полутолщины и высоты минимумов слоев. Параметры корреляционной функции неопределенности диэлектрической проницаемости канала были взяты: μ2 = 0,0004, a = 10 км, V = 50 м/c. Для данных параметров определялись среднеквадратичные отклонения траекторных характеристик пробного сигнала на частоте f = 45 МГц. Координаты пробного источника были взяты: хр = 2990 км, zр = 1500 км. Параметры модели (6) составляли: fкрЕ = 4 МГц, fкр = 8 МГц, ymE = 40 км, ym = 150 км, zmE = 140 км, zm = 400 км. Рассчитанные («измеренные») значения флуктуационных характеристик пробного сигнала составили: среднеквадратичные отклонения фазового пути σФр = (σφрс) / (2πf) = 27 м, доплеровского смещения частоты σfр = 0,04 Гц, группового пути σ∆Lр = cσ∆tр = 40.2 м «Измеренные» дисперсии характеристик пробного сигнала являлись входными величинами для расчета возможных дисперсий флуктуационных характеристик основных сигналов на заданных дистанциях. Интегральные коэффициенты, входящие в алгебраические уравнения (3), были получены в результате расчета дифференциальных уравнений (4) с начальными условиями (5). Соответствующие величины среднеквадратичных отклонений представлены в табл. 1. Выполненные расчеты показали, что величины возможных статистических характеристик доплеровского смещения частоты, направления прихода (в градусах), групповой и фазовой задержки основных сигналов в информационном канале с неопределенностью параметров соответствуют теории рассеяния волн в среде с крупномасштабными (по сравнению с размером зоны Френеля) неоднородностями [6, с. 113].

Для канала с отражением входными данными являлись статистические характеристики принятого пробного сигнала, рассчитанные вдоль отраженной траектории, соединяющей корреспондентов, при заданной неопределенности параметров канала. Для описания диэлектрической проницаемости регулярного канала, как и выше, использовалась модель (6). Соответствующие модельные параметры были взяты: fкрЕ = 4 МГц, fкр = 8 МГц, ymE = 35 км, ym = 120 км, zmE = 150 км, zm = 320 км. Выбирались три дистанции для передачи сигналов из основного источника на различных рабочих частотах: хк = 1765 км (f = 16МГц), хк = 1725 км (f = 14МГц) и хк = 1868 км (f = 18МГц). В качестве пробной была выбрана дистанция хр = 1700 км (f = 15МГц). Величины неопределенности параметров канала на пробной дистанции были взяты: μ2 = 0,0004, a = 10 км, V = 100 м/c. Для этих параметров расчеты флуктуационных характеристик пробного сигнала дают 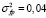Гц2 (σfр = 0,2Гц), 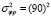(среднеквадратичное отклонение фазового пути σФр = (σφрс) / (2πf) = 286 м), 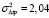мкс2 (среднеквадратичное отклонение группового пути σ∆Lр = cσ∆tр = 428 м). Найденные величины дисперсий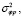 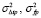пробного сигнала и вычисленные с помощью системы (4) коэффициенты J1, J2, J3, J4, G1, G2, G3, G4, G5, G6 были использованы в (3) для расчета возможных флуктуаций траекторных характеристик основных сигналов на заданных дистанциях. Результаты расчетов статистических характеристик сигналов на рассмотренных трассах представлены в табл. 2. Анализ показал, что возможные среднеквадратичные отклонения доплеровского смещения частоты, направления прихода, групповой и фазовой задержки сигналов в информационном канале с заданными корреляционными свойствами неопределенности параметров соответствуют общепринятым представлениям статистической радиофизики [6, с. 113].

Таблица 1

Ожидаемые флуктуации характеристик сигнала в канале с просвечиванием

Таблица 2

Ожидаемые флуктуации характеристик сигналов в канале с отражением

Заключение

Развит метод быстрой оценки возможных статистических моментов траекторных характеристик сигналов в информационном канале с неопределенностью параметров по данным наблюдений флуктуационных характеристик сигнала, излученного из пробного источника. Для трехмерного канала получены алгебраические уравнения связи дисперсий доплеровского смещения частоты, направления прихода, групповой и фазовой задержек основных и пробного сигналов. Интегральные коэффициенты этих уравнений определены в результате решения краевых стохастических задач с условиями Дирихле для основных и пробного источников. Интегралы для коэффициентов сведены к системе линейных дифференциальных уравнений первого порядка с начальными условиями Коши. В качестве модели неопределенности параметров канала использована пространственно-временная корреляционная функция, учитывающая пространственную динамику диэлектрической проницаемости регулярного канала. Для описания временных флуктуаций параметров диэлектрической проницаемости использовано приближение вмороженного переноса. Развитый метод диагностики позволяет проводить экспресс-оценку возможных флуктуаций сигналов в стохастическом информационном канале как в режиме просвечивания, так и в условиях отражения. Для практической реализации метода оперативной диагностики ожидаемых флуктуаций характеристик сигналов в условиях неопределенности параметров канала связи достаточно иметь модель диэлектрической проницаемости регулярного канала.

Библиографическая ссылка