Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Базилевский М.П. 1

---

1 ФГБОУ ВО «Иркутский государственный университет путей сообщения»

Статья посвящена исследованию задачи отбора наиболее информативных регрессоров в модели множественной линейной регрессии, оцениваемой с помощью метода наименьших квадратов. Ранее эта задача была формализована в виде задачи частично-булевого линейного программирования. В полученной в результате ее решения линейной регрессии интеркорреляции объясняющих переменных могли быть статистически значимыми, что затрудняло интерпретацию ее оценок из-за мультиколлинеарности. В данной статье для контроля в процессе отбора наиболее информативных регрессоров абсолютных величин интеркорреляций в задачу частично-булевого линейного программирования введены специальные линейные ограничения. В результате сформулирована задача, решение которой приводит к построению линейной регрессии с оптимальным по коэффициенту детерминации числом объясняющих переменных, в которой абсолютные величины интеркорреляций не превосходят заданного числа. Помимо этого знаки оценок линейной регрессии согласуются со знаками соответствующих коэффициентов корреляции, а абсолютные вклады переменных в общую детерминацию не меньше заданного числа. С помощью предложенных линейных ограничений на интеркорреляции сформулированы задачи булевого линейного программирования, позволяющие выделять в корреляционной матрице кластеры слабо и высоко коррелирующих переменных. Проведено успешное тестирование предложенного математического аппарата.

Статья в формате PDF

352 KB

линейная регрессия

отбор информативных регрессоров

задача частично-булевого линейного программирования

метод наименьших квадратов

интеркорреляция

кластеризация

мультиколлинеарность

1. Konno H., Yamamoto R. Choosing the best set of variables in regression analysis using integer programming // Journal of Global Optimization. 2009. Vol. 44. P. 273–282. DOI: 10.1007/s10898-008-9323-9.

2. Miyashiro R., Takano Y. Mixed integer second-order cone programming formulations for variable selection in linear regression // European Journal of Operational Research. 2015. Vol. 247. P. 721–731. DOI: 10.1016/j.ejor.2015.06.081.

3. Miyashiro R., Takano Y. Subset selection by Mallows’ Cp: A mixed integer programming approach // Expert Systems with Applications. 2015. Vol. 42. P. 325–331. DOI: 10.1016/j.eswa.2014.07.056.

4. Park Y.W., Klabjan D. Subset selection for multiple linear regression via optimization // Journal of Global Optimization. 2020. Vol. 77. P. 543–574. DOI: 10.1007/s10898-020-00876-1.

5. Takano Y., Miyashiro R. Best subset selection via cross-validation criterion. Top. 2020. Vol. 28, Is. 2. P. 475–488. DOI: 10.1007/s11750-020-00538-1.

6. Bertsimas D., Li M.L. Scalable holistic linear regression // Operations Research Letters. 2020. Vol. 48, Is. 3. P. 203–208. DOI: 10.1016/j.orl.2020.02.008.

7. Chung S., Park Y.W., Cheong T. A mathematical programming approach for integrated multiple linear regression subset selection and validation // Pattern Recognition. 2020. Vol. 108. DOI: 10.1016/j.patcog.2020.107565.

8. Tamura R., Kobayashi K., Takano Y., Miyashiro R., Nakata K., Matsui T. Mixed integer quadratic optimization formulations for eliminating multicollinearity based on variance inflation factor // Journal of Global Optimization. 2019. Vol. 73. P. 431–446.

9. Watanabe A., Tamura R., Takano Y., Miyashiro R. Branch-and-bound algorithm for optimal sparse canonical correlation analysis // Expert Systems with Applications. Vol. 217. P. 119530. DOI: 10.1016/j.eswa.2023.119530.

10. Bertsimas D., Gurnee W. Learning sparse nonlinear dynamics via mixed-integer optimization. Nonlinear Dynamics. 2023. Vol. 111. No. 7. P. 6585–6604. DOI: 10.1007/s11071-022-08178-9.

11. Базилевский М.П. Отбор информативных регрессоров с учетом мультиколлинеарности между ними в регрессионных моделях как задача частично-булевого линейного программирования // Моделирование, оптимизация и информационные технологии. 2018. Т. 6. № 2 (21). С. 104–118.

12. Базилевский М.П. Отбор оптимального числа информативных регрессоров по скорректированному коэффициенту детерминации в регрессионных моделях как задача частично целочисленного линейного программирования // Прикладная математика и вопросы управления. 2020. № 2. С. 41–54.

13. Базилевский М.П. Отбор значимых по критерию Стьюдента информативных регрессоров в оцениваемых с помощью МНК регрессионных моделях как задача частично-булевого линейного программирования // Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. 2021. № 3. С. 5–16.

14. Базилевский М.П. Построение вполне интерпретируемых линейных регрессионных моделей с помощью метода последовательного повышения абсолютных вкладов переменных в общую детерминацию // Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. 2022. № 2. С. 5–16.

Аппарат математического программирования на сегодняшний день успешно применяется для отбора наиболее информативных регрессоров (ОИР) в регрессионных моделях. В зарубежной литературе такая процедура известна как «feature selection», «subset selection» и т.д. При этом в иностранных источниках задача ОИР в основном сводится к задаче частично-булевого квадратичного программирования (ЧБКП). Одна из первых таких формализаций для линейных регрессий, оцениваемых с помощью метода наименьших квадратов (МНК), была представлена в [1]. В [2] сформулирована задача ОИР на основе скорректированного коэффициента детерминации и информационных критериев Акаике и Шварца, в [3] – на основе критерия Мэллоуза, в [4] – на основе критериев среднеквадратичных и абсолютных ошибок, в [5] – на основе критерия кросс-валидации. В [6] исследуется целостная линейная регрессия, для которой сформулирована задача ОИР с ограничениями на значимость коэффициентов и степень мультиколлинеарности, а в [7] осуществляется так называемая регрессионная диагностика с использованием линейных ограничений на наблюдаемые значения t-критерия Стьюдента. В [8] сформулирована задача ОИР для устранения мультиколлинеарности с помощью факторов «вздутия» дисперсии, в [9] разработан алгоритм для решения задачи максимизации канонической корреляции, а в [10] сформулирована задача для выявления уравнений сложных динамических систем.

В [11–14] автором предложены различные формализации задачи ОИР в линейной регрессии, оцениваемой с помощью МНК, в виде задач частично-булевого линейного программирования (ЧБЛП). Для контроля мультиколлинеарности в [11] использованы ограничения на факторы «вздутия» дисперсии. Однако этих ограничений недостаточно для того, чтобы гарантировать отсутствие значимой корреляции абсолютно между всеми парами объясняющих переменных, что необходимо для корректного объяснения полученных с помощью МНК оценок.

Цель исследования состоит в формализации задачи ОИР для линейной регрессии, оцениваемой с помощью МНК, в виде задачи ЧБЛП с линейными ограничениями на корреляции объясняющих переменных (интеркорреляции).

Материалы и методы исследования

Модель множественной линейной регрессии имеет вид

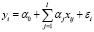, i = 1,n, (1)

где yi, i = 1,n – значения объясняемой (зависимой) переменной y; xij, i = 1,n, j = 1,l – значения l объясняющих (независимых) переменных x1, x2,…, xl; n – объем выборки; αj, j = 0,l – неизвестные параметры; εi, i = 1,n – ошибки аппроксимации.

Задача ОИР для модели (1), оцениваемой с помощью МНК, формулируется следующим образом: необходимо из l объясняющих переменных выбрать m наиболее информативных так, чтобы либо сумма квадратов остатков модели была минимальна, либо коэффициент детерминации R2 был максимален.

Проведем нормирование (стандартизацию) всех переменных по правилам:

, , ..., ,

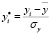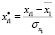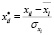i = 1,n,

где 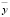, , 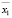…, 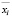– средние значения переменных, 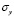, , 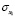…, 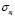– среднеквадратические отклонения переменных.

Составим модель стандартизованной линейной регрессии:

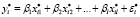, i = 1,n, (2)

где β1, …, βl – неизвестные параметры; 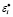, i = 1,n – ошибки аппроксимации.

МНК-оценки стандартизованной регрессии (2) находятся по формуле

,

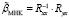где – матрица

интеркорреляций;

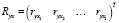– вектор корреляций объясняющих переменных с y.

В [14] сформулирована следующая задача ЧБЛП для ОИР в модели (2):

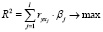(3)

,

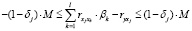j = 1,l, (4)

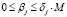, j ∈ J+, (5)

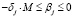, j ∈ J–, (6)

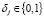, j = 1,l, (7)

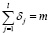, (8)

в формуле (8)

M – большое положительное число, J+ и J– – сформированные из множества 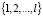индексные подмножества, элементы которых удовлетворяют условиям 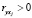и .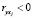

Решение задачи ЧБЛП (3)–(8) приводит к построению оптимальной по критерию R2 линейной регрессии с m объясняющими переменными, в которой знаки коэффициентов согласованы со знаками соответствующих корреляций вектора Rxy. Для того чтобы можно было объяснить полученные оценки, еще до решения задачи (3)–(8) необходимо исключать все объясняющие переменные, противоречиво коррелирующие с y. Для объяснения необходимо использовать МНК-оценки модели (1), связанные с МНК-оценками регрессии (2) формулами

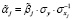, j = 1,l,

.

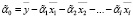Пусть множество Ф содержит номера отобранных переменных. Поскольку для оцененной линейной регрессии выполняются условия 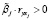, j ∈ Ф, то становятся справедливыми следующие формулы для абсолютных вкладов переменных в общую детерминацию R2:

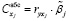, j ∈ Ф.

С помощью этих коэффициентов можно контролировать степень влияния любой объясняющей переменной на y. Поэтому в [14] было предложено в задаче (3)–(8) заменить линейное ограничение (8) на следующее:

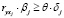, j = 1,l (9)

где θ ≥ 0 – назначенный исследователем наименьший вклад входящих в модель объясняющих переменных в общую детерминацию R2. Чем выше значение θ, тем больше переменных «выдавливается» из модели, следовательно, регрессия становится проще и снижается эффект мультиколлинеарности.

Таким образом, решение задачи ЧБЛП (3)–(7), (9), приводит к построению линейной регрессии с оптимальным по критерию R2 количеством объясняющих переменных, в которой 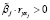, j ∈ Ф, и вклады 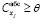, j ∈ Ф.

Для контроля в оптимизационной задаче ОИР абсолютных величин интеркорреляций введем следующие линейные ограничения:

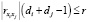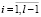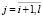, , ,(10)

где 0 ≤ r ≤ 1 – назначенная исследователем наибольшая величина абсолютных интеркорреляций входящих в модель объясняющих переменных. Если r = 0, то в построенной регрессии все интеркорреляции должны быть равны 0, а если r = 1, то нет ограничений на величины интеркорреляций в оцененной модели.

Если в ограничении (10) 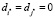, что означает, что ни i*-я, ни j*-я переменная не входят в регрессию, то оно принимает вид 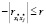, поэтому справедливо всегда. Если в ограничении (10) либо 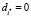, , 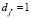либо 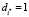, 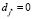(в модель входит либо i*-я, либо j*-я переменная), то оно принимает вид 0 ≤ r, поэтому справедливо всегда. Если же в ограничении (10) 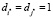(в модель входит и i*-я, и j*-я переменная), то оно принимает вид 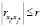. В последнем случае, если 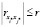выполняется, то i*-я и j*-я переменные могут входить в модель одновременно, а если не выполняется, то нет.

Заметим, что общее число ограничений (10) может быть сокращено. Действительно, если 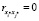, то ограничение (10) выполняется для любых значений бинарных переменных. Аналогично, если 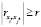. Тогда ограничения (10) следует переписать в виде

,

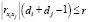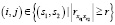(11)

Таким образом, решение задачи ЧБЛП (3)–(7), (9), (11) приводит к построению линейной регрессии с оптимальным по критерию R2 количеством объясняющих переменных, в которой 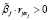, j ∈ Ф, вклады 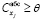, j ∈ Ф, и интеркорреляции 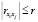, i, j ∈ Ф, i < j.

Предложенные ограничения (11) на величины интеркорреляций могут быть использованы для формализации задачи кластеризации корреляционной матрицы. Эта задача может быть сформулирована следующим образом: необходимо из l объясняющих переменных выбрать как можно больше переменных так, чтобы все их интеркорреляции не превосходили числа r.

Эта задача может быть формализована в виде задачи булевого линейного программирования (БЛП) с целевой функцией

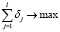(12)

и линейными ограничениями (7), (11).

Ее решение позволяет сформировать кластер слабо коррелирующих объясняющих переменных (КСКП).

Аналогично можно сформулировать задачу отбора из l объясняющих переменных наибольшего числа переменных так, чтобы все их интеркорреляции были не меньше числа r. Она формализуется в виде задачи БЛП с целевой функцией (12), линейными ограничениями (7) и

,

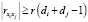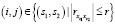(13)

Решение задачи (12), (7), (13) позволяет сформировать кластер высоко коррелирующих объясняющих переменных (КВКП).

Заметим, что сформулированные задачи БЛП могут иметь несколько оптимальных решений.

Результаты исследования и их обсуждение

Для тестирования предложенного математического аппарата были использованы встроенные в эконометрический пакет Gretl статистические данные о зарплатах игроков НБА (data7-20.gdt). Для удобства были исключены все фиктивные переменные и составлена выборка из первых 30 наблюдений для зависимой переменной SALARY и оставшихся 17 объясняющих переменных. Для решения оптимизационных задач использовался решатель LPSolve IDE на персональном компьютере с 4-ядерным процессором (3100 МГц) и оперативной памятью 4 Гб. Для заданного числа r решалась задача ЧБЛП (3)–(7), (11) (без ограничений на вклады), задача БЛП (12), (7), (11) и задача БЛП (12), (7), (13). Для удобства назовем их задача A, задача B и задача C соответственно. В результате решения задачи A фиксировались номера отобранных переменных, время решения t в секундах и коэффициент детерминации R2. А в результате решения задач B и C фиксировалось число отобранных переменных m и время решения t. Результаты тестирования представлены в таблице. Большое число M для решения задачи A выбиралось так, как это предложено делать в [14].

По таблице видно, что LPSolve IDE справился со всеми задачами практически мгновенно. Как и ожидалось, при решении задачи A с уменьшением числа r, т.е. с ужесточением требования на объясняющие переменные с высокими интеркорреляциями, число отобранных переменных в линейной регрессии снижается. При этом также снижается время решения задачи и значение коэффициента детерминации. А время решения задач B и С практически не менялось в зависимости от выбранных значений r. При этом в задаче B с уменьшением r объем кластера слабо коррелирующих переменных уменьшался, а в задаче C объем кластера высоко коррелирующих переменных увеличивался. Полученные результаты подтверждают корректность предложенного математического аппарата.

Заключение

В результате проведенных исследований сформулирована задача ЧБЛП, решение которой приводит к построению линейной регрессии с оптимальным по критерию R2 числом объясняющих переменных, в которой знаки оценок согласуются со знаками соответствующих коэффициентов корреляции 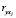, абсолютные вклады переменных не меньше числа θ, а интеркорреляции не превосходят числа r. Построенная регрессионная модель гарантированно может быть интерпретирована, если на начальном этапе были исключены все противоречиво коррелирующие с y объясняющие переменные.

Результаты решения задач

Помимо этого разработанные линейные ограничения на интеркорреляции позволили сформировать задачи БЛП для построения кластеров слабо и высоко коррелирующих переменных. Первый из них способствует построению традиционных моделей множественной линейной регрессии, а второй – моделей полносвязной линейной регрессии, в которых все объясняющие переменные связаны между собой. В дальнейшем планируется провести тестирование предложенного математического аппарата для построения регрессионных моделей по выборкам большого объема.

Библиографическая ссылка