Прогнозирование пригодности сырья для нужд термической переработки, выбор рациональных схем и режимная адаптация энергоемких аппаратов горно-обогатительной отрасли к периодически изменяющимся свойствам рудного сырья сталкиваются с трудностями, обусловленными устаревшими подходами к моделированию и методам расчета процессов термической подготовки и переработки, достаточно полно учитывающим специфические особенности и свойства фосфатного сырья. Поиск оптимальных условий протекания процессов на действующем оборудовании представляет собой весьма сложную и дорогостоящую задачу из-за большого количества факторов, влияющих на конечный результат протекающих химико-технологических процессов. Поэтому в настоящее время оптимальным способом изучения и последующей рационализации протекающих при термической обработке фосфатного рудного сырья процессов является метод построения математических и компьютерных моделей, точно описывающих все особенности и составляющие химико-технологических превращений и позволяющих провести анализ и спрогнозировать изменения исходного рудного материала, повышая качество готовой продукции и выбирая наиболее энергоресурсоэффективные режимы работы оборудования. Математическое моделирование процессов образования и переноса пылевых шламовых частиц является одним из актуальных направлений для анализа и понимания путей совершенствования технологии электротермического производства фосфора. Вначале рассмотрим унос капель жидкости – расплава, который зависит от скорости газов, барботирующих расплав. Для этого следует проанализировать механизмы формирования газового потока в реакционной зоне электротермического реактора, в котором принято разделение на несколько областей: зона шихты, зона расплава, углеродистая зона, зона ферросплава, зона шлакообразования.
Восстановительная реакция фосфора 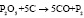 , при помощи которой возможно стехиометрически описать компоненты реакции, в свою очередь позволяет выбрать направление разработки и моделирования реактора [1, 2].
, при помощи которой возможно стехиометрически описать компоненты реакции, в свою очередь позволяет выбрать направление разработки и моделирования реактора [1, 2].
Влияние управляющих параметров на процессы, протекающие в рудно-термической печи (РТП), можно оценить, применив приближенное описание ее состояний с помощью применения сосредоточенных параметров.
Для этого были конкретизированы вектора:
– входной вектор
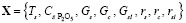 ,
,
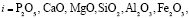
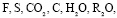 Лет, Проч.
Лет, Проч.
где R2O – общее обозначение не конкретизированных в списке оксидов, Лет – летучие фракции, Проч – прочие соединения;
– выходной вектор
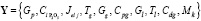 ,
,
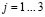 ;
;
– управляющий вектор
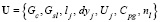 ;
;
– вектор состояния
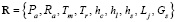 ,
,
где Ts – температура сырья на входе в рудно-термическую печь, Tg – температура газов на выходе в пространстве свода рудно-термической печи, Tm – температура начала процесса расплавления шихты, Tl – температура расплавленной шихты, Tr – температура жидкой фазы реакционной зоны, Cpg – концентрация фосфора, 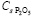 – концентрация фосфоросодержащих окисей в исходном сырье,
– концентрация фосфоросодержащих окисей в исходном сырье, 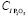 – концентрация фосфоросодержащих окисей в расплаве, Cdg – концентрация частиц пыли в отводных газах, hc – высота коксовой зоны, Gg – расход печных газов, Cl – расход шлака, Cc – расход кокса, Csl – расход кварцита, Cp – расход фосфора в зоне выхода, Cs – расход шихты, hl – высота шлака, hs – высота шихтовой зоны; lj – перемещение j-го электрода, dyj – перепуск j-го электрода, Lj – положение задействованных концов электродов (абсолютное); Uj – фазное напряжение, Jel j – плотность тока j-го электрода.
– концентрация фосфоросодержащих окисей в расплаве, Cdg – концентрация частиц пыли в отводных газах, hc – высота коксовой зоны, Gg – расход печных газов, Cl – расход шлака, Cc – расход кокса, Csl – расход кварцита, Cp – расход фосфора в зоне выхода, Cs – расход шихты, hl – высота шлака, hs – высота шихтовой зоны; lj – перемещение j-го электрода, dyj – перепуск j-го электрода, Lj – положение задействованных концов электродов (абсолютное); Uj – фазное напряжение, Jel j – плотность тока j-го электрода.
Характеристики гранулометрического состава шихты: rs – средний радиус частиц фосфорита, Mk – модуль кислотности, rc – средний радиус частиц кокса, rsl – средний радиус частиц кварцита, nl – количество открытых леток, Pa – активная полезная мощность; Ra – сопротивление реакционной зоны.
В реакционной зоне возможно записать уравнение энергетического баланса в следующем виде:
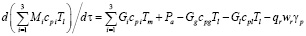 . (1)
. (1)
Масса вступающих в превращения компонентов оксида фосфора, кокса и расплава постоянна и описывается как
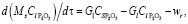 (2)
(2)
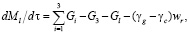 (3)
(3)
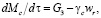 (4)
(4)
Принимая следующие начальные условия:
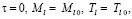
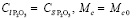 ,
,
где Mi – массы i-х компонентов: i = 1, G1, Ms – для фосфорита, i = 2, G2, Ml – для расплава, i = 3, G3, Mc – для кокса; cpi – теплоемкости i-х компонентов, wr – скорость восстановительной реакции оксида фосфора P2O5, γi – коэффициент, учитывающий пересчет реагента для i-го компонента, qr – тепловой эффект реакции.
Состав газов определяется преимущественно из соотношений концентраций окисей фосфора и углерода [3]. Скорость реакций восстановления определяет расход газов и вычисляется как Gg = γgwr и зависит от стехиометрических условий: 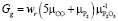 , в которых молярные веса оксида фосфора
, в которых молярные веса оксида фосфора 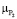 и углерода μCO.
и углерода μCO.
Цель исследования – построение математической модели процессов формирования шлама при переработке рудного фосфатного сырья в рудно-термических печах с перспективой управления их энергоресурсоэффективностью, на основе использования гидродинамического подхода. Модель должна учитывать теплогидравлические особенности нестационарных состояний фосфорной рудно-термической печи в приближении сосредоточенных параметров, а также перемещение капель расплава с барботирующими газами, что является главной причиной появления пыли в расплаве.
Материалы и методы исследования
Подача шихты в реакторную зону происходит непрерывно и, благодаря наличию режима саморегуляции объекта, обеспечивается состоянием равновесия системы [4]. Природа этого явления объясняется тем, что температура и геометрия (высота) коксового слоя определяет формирование геометрии ванны РТП.
На границах дисперсной и жидкой фазы происходит процесс расплавления шихты при барботировании печных газов. На этой границе отдельные твердые фракции шихты имеют температуру плавления, в то время как газы, выходящие из жидкой фазы, имеют температуру выше температуры плавления. Эти условия дают возможность найти расход шихты, основываясь на тепловом балансе фазового перехода:
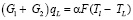 ,
,
где TL – температура плавления, α – коэффициент теплоотдачи, F – поверхность теплообмена в зоне плавления, qL – удельная теплота расплава шихтовых материалов.
Создаваемый слоем шлакового расплава, шихты и кокса гидравлический напор создает условия для слива шлака (непрерывного или периодического) через шлаковые летки с расходом
Gsl = f(ξ) nl Sl wl,
где wl – выходная скорость шлака из летки, f(ξ) – функция сопротивления при протекании шлака через летки.
Из соотношения
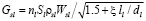
возможно определить расход шлака при сливе из печи, который определяется согласно гидродинамическим законам, которые описывают закономерности истечения жидкости из сосуда через трубу конечной длины ll, где dl – диаметр летки, ξ – коэффициент сопротивления, ρsl – плотность шлака, nl = 0,1,2 – количество действующих леток; 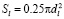 – площадь поперечного сечения отверстия летки, Wsl – скорость вытекания шлака через отверстие летки. Коэффициент сопротивления рассчитывают по формуле, учитывающей μsl – динамическую вязкость шлака:
– площадь поперечного сечения отверстия летки, Wsl – скорость вытекания шлака через отверстие летки. Коэффициент сопротивления рассчитывают по формуле, учитывающей μsl – динамическую вязкость шлака:
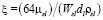 .
.
Формула расчета скорости истечения шлака через летку:
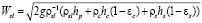 ,
,
где εc – порозность слоя кокса, ρs – плотность материала шихты, εs – порозность слоя шихты, hc – высота зоны кокса, hp – высота зоны расплава, hs – высота шихтовой зоны, которые определяются по формулам
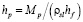 ,
,
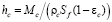 ,
,
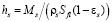 ,
,
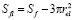 ,
,
где rel – радиус электродов плавильной печи.
Выражения для противоточного энергообмена используются для нахождения температур газов tg и шихты ts в шихтовой зоне плавильной печи. Необходимо понимать, что скорость процессов химических превращений в реакционной зоне на порядок ниже скорости конвективного теплопереноса в соответствующей зоне; это позволяет считать выполненным условие стационарности [5, 6]. Для противоточного теплообменника возможно определить температуру шихты на входе в реакционную зону, которая записана с помощью операторного матричного соотношения для 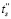 :
:
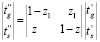 ,
,
где 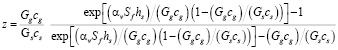 ,
,
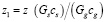 ,
,
где t’s – температура шихты на выходе из реакционной зоны, α – коэффициент теплоотдачи, t’g, t’’g – температуры газа соответственно на выходе и входе в реакционную зону, ds – средний диаметр частиц шихты, αv = α6(1 – ε) / ds – объемный коэффициент теплообмена между шихтой и газом. Система является довольно инерционной, в реакционной зоне время реагирования пятиокиси фосфора P2O5 может длиться, согласно экспериментальным данным, достаточно продолжительное время, достигающее одного часа и более. Поэтому прогнозирование поведения системы при воздействиях различного рода является весьма важной задачей. Результаты вычислительных экспериментов подтвердили актуальность построенных математических моделей и их соответствие данным натурного эксперимента (рисунок).
В реакционной зоне возможно записать аппроксимированную зависимость, описывающую выделение энергии:
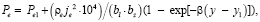
где β – эмпирический коэффициент, Pe1 – мощность на электродах в положении y1, Pe – мощность на электродах в положении y.
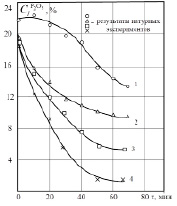
Зависимость концентрации P2O5 в реакционной зоне от температуры при различных значениях температуры расплава, где 1 – 1400 °C, 2 – 1450 °C, 3 – 1500 °C, 4 – 1550 °C
Динамическую математическую модель плавильной рудно-термической фосфорной печи возможно описать системой уравнений в приближении сосредоточенных параметров [7]. Предлагаемый подход может быть распространен без существенных изменений и на технологии, тождественные процессу производства фосфора по своему механизму протекания.
Эта же система уравнений при условии замены производных нулевыми значениями подходит и для описания стационарного режима состояния печи.
Предложенная математическая модель позволяет сымитировать состояние рудно-термической печи в различных ситуациях и режимах, а также при различных значениях параметров управления проанализировать поведение объекта [8, 9].
Основываясь на рассмотренных выше уравнениях сохранения массы и энергии, возможно провести описание стационарных состояний фосфорной рудно-термической печи в приближении сосредоточенных параметров для реакционной зоны плавильной печи.
Расход шихты, попадающей в плавильную рудно-термическую печь, возможно определить режимом работы печи 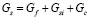 . Шихта состоит из кремнистых разностей фосфоритов, кварцитов и кокса – восстановителя фосфора. Дозировки компонентов кварцитов, кокса, фосфоритов относительно расхода шихты возможно определить по соотношению:
. Шихта состоит из кремнистых разностей фосфоритов, кварцитов и кокса – восстановителя фосфора. Дозировки компонентов кварцитов, кокса, фосфоритов относительно расхода шихты возможно определить по соотношению:
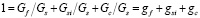 ,
,
где 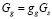 – расход газа,
– расход газа, 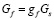 – расход фосфорита, gi – массовые доли компонентов шихты,
– расход фосфорита, gi – массовые доли компонентов шихты, 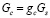 – расход кокса,
– расход кокса, 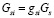 – расход кварцита.
– расход кварцита.
Проанализировав стехиометрию реакции 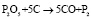 определили, что при условии небольшой концентрации P2O5 в шлаке коэффициент расхода шихты относительно расхода газа возможно представить в виде:
определили, что при условии небольшой концентрации P2O5 в шлаке коэффициент расхода шихты относительно расхода газа возможно представить в виде:
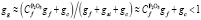 ,
,
где 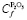 – содержание пятиокиси фосфора в руде.
– содержание пятиокиси фосфора в руде.
Из уравнения баланса P2O5 и кокса можно получить:
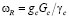 ,
, 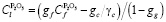 .
.
При 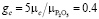 ;
; 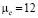 ;
; 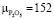 ;
; 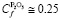 .
.
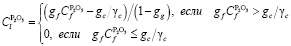 .
.
В реакционной зоне можно принять без больших погрешностей среднюю концентрацию P2O5: 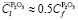 .
.
В объеме печи возможно записать энергетический баланс:
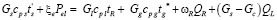 ,
,
где tL, tR – температура плавления и расплава; QR – тепловой эффект реакции восстановления, ωR – скорость и реакции восстановления, t’s – температура рудного сырья на входе в печь, ξe – доля печи, используемая для реакционной зоны, cpg – теплоемкость газа, cps – теплоемкость шихты, cpl – теплоемкость шлака, t*g – температура печных газов в пространстве сводов печи, Pel – мощность печи, QL – теплота плавления.
Балансы компонентов массы для пятиокиси фосфора:
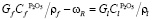 ,
,
где 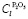 – концентрация пятиокиси фосфора в расплаве,
– концентрация пятиокиси фосфора в расплаве, 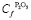 – содержание пятиокиси фосфора в руде; для кокса:
– содержание пятиокиси фосфора в руде; для кокса: 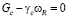 . Общий массовый баланс возможно записать как:
. Общий массовый баланс возможно записать как: 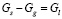 .
.
Анализ соотношений, которые при применении комбинированного подхода будут в объеме печи учитывать распределенность параметров, позволит получить необходимые зависимости для проведения комплексного анализа процессов, протекающих в высокотемпературной зоне [10, 11]. На границе фазовых переходов соотношение энергетического баланса возможно записать в виде
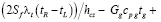
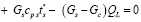 .
.
Учитывая условия энергетического баланса энергии в зоне шихты, возможно записать приближенное равенство 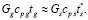 Тогда для расчета расхода шихты справедливо будет записать:
Тогда для расчета расхода шихты справедливо будет записать:
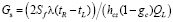 .
.
В реакционной зоне, из усредненного выражения записи уравнения энергетического баланса, возможно записать зависимость
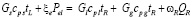 ,
,
а учитывая мощность, получим
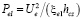 ,
,
где 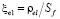 .
.
Выражение для температуры в зоне реакции возможно записать как
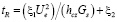 ,
,
где 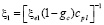 ,
, 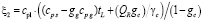 .
.
Подставив в уравнение для температуры выражение для расхода шихты, получим следующее суммирующее выражение:
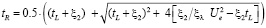 .
.
Мощность печи возрастает при повышении напряжения и, наоборот, с ростом доли кокса в шихте убывает. При увеличении дозировки кокса температура внутри печи снижается, а с повышением напряжения начинает возрастать [12]. В макропредставлении скорость протекания химической реакции восстановления примет вид
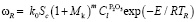 ,
,
где rcp – средний радиус частиц, Mc – масса кокса в реакционной зоне, k0 – предэкспоненциальный множитель, равный k0 = 1,6 × 108 кг/(м2с),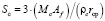 – площадь поверхности коксовых частиц, Af – коэффициент формы частиц кокса, Е – энергия активации, E / R = 48000 K-1.
– площадь поверхности коксовых частиц, Af – коэффициент формы частиц кокса, Е – энергия активации, E / R = 48000 K-1.
Условия протекания реакции восстановления фосфора определяют расход газа:
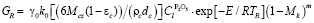 .
.
Возможно записать линеаризованную аррениусовскую функцию для расхода газа:
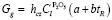 ,
,
где 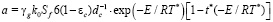 ,
,
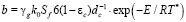 .
.
Производительность, запыленность и, соответственно, расход газа возрастут при увеличении напряжения и, напротив, будут уменьшаться при увеличении внесения кокса в печь. Формирование коксовой зоны определяется на основании коксового баланса в печи, который учитывает высоту коксовой зоны, зависящую от условий расходования и поступления кокса:
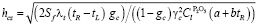 .
.
Размеры коксовой зоны увеличиваются при увеличении подачи кокса, а ее уменьшению способствует повышение напряжения [13].
Из выражения энергетического баланса шихтовой зоны на выходе из печи получается температура газов:
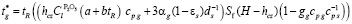 .
.
Отсюда следует положительное влияние напряжения и негативное воздействие подачи кокса. Справедливым будет считаться: 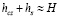 . Согласно закону сохранения масс возможно записать выражение для расхода шлака через летки:
. Согласно закону сохранения масс возможно записать выражение для расхода шлака через летки:
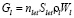 ,
,
где H – высота ванны печи, Mcz – масса слоя кокса, 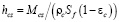 – высота реакционной зоны.
– высота реакционной зоны.
С учетом распределенности концентрация реагента на выходе из печи будет
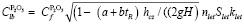 .
.
Приняв во внимание, что производительность по фосфору связана с расходом газа через постоянный стехиометрический коэффициент, из балансового уравнения энергии в печи возможно получить удельный расход электроэнергии, являющийся основным показателем энергоресурсоэффективности плавильной печи [14].
Снижение потерь продукта, обусловленных шлакообразованием, обеспечивают развитая коксовая зона и условия повышенной температуры [15]. Для расчета удельного расхода электроэнергии запишем выражение
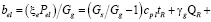
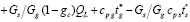 .
.
Результаты исследования и их обсуждение
Проанализировав полученные математические модели, возможно провести описание основных тепловых процессов, протекающих во время работы плавильной рудно-термической печи. Управляющие параметры, такие как напряжение на электродах и дозировка кокса, влияют на удельный расход энергии и зависят от промежуточных технологических показателей: расхода газа, высоты коксовой зоны, расхода шихты, температуры в реакционной зоне. Снижение дозировки кокса снижает удельный расход энергии, как и при повышении напряжения на электродах. Для нахождения оптимальных условий функционирования плавильного оборудования возможно минимизировать функции удельного расхода, принимая во внимание ограничения, которые необходимо учесть по всем показателям, например используя метод штрафных функций. Важным параметром является соотношение напряжения и мощности, определяющееся по высоте коксовой зоны и зависящее от режима функционирования печи. Сопротивление зоны реагирования характеризует размер коксовой зоны, откуда весьма сложный механизм формирования электрического режима печи становится понятным.
Вторая из предложенных моделей характеризует унос частиц в рудно-термической печи барботирующими газами из расплава и описывает процесс образования шлама, который образуется при появлении пылевых отходов техногенного характера, образующихся при переработке апатит-нефелиновых руд и являющихся основной причиной появления загрязнения фосфора шламовыми продуктами в зоне выхода из печи. Она основана на том факте, что главной причиной образования пыли в расплаве рудного фосфорсодержащего сырья является отвердевание уносимых барботирующими газами капель расплава и образование из них твердых частиц наряду с процессами возгонов, конденсации и испарения вместе с химическими реакциями в газовой фазе. На степень запыленности расплава будут влиять скорость движения газа, поверхностное натяжение, плотность расплава, химический состав шихты, электрическое сопротивление расплава и т.д. При проведении моделирования зависимости уноса капель от критерия Вебера необходимо учесть наличие режимного параметра для рудно-термической печи, а также зависимость массы капель в единице массы газа от скорости истечения газа в вертикальном канале на колоснике печи.
В единице массы газа зависимость массы капель в единице массы газа возможно записать как
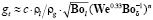 , (5)
, (5)
где c – константа, gt – масса капель в единице массы газа, ρl – плотность жидкости, ρg – плотность газа, c = 50, We – критерий Вебера, Bo – критерий Бонда, n = 2 / s, где s – дисперсия логарифмически нормального распределения, s ≈ 1. При этом 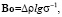
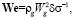 σ – коэффициент поверхностного натяжения жидкой фазы, l, δ – характерный размер системы, g – ускорение свободного падения, ∆ρ = ρl – ρg.
σ – коэффициент поверхностного натяжения жидкой фазы, l, δ – характерный размер системы, g – ускорение свободного падения, ∆ρ = ρl – ρg.
Полученное выражение для технологических реакторов различных типов обобщает зависимости уноса капель от являющегося режимным параметром критерия Вебера We. В настоящее время существует мнение, что унос жидкости обуславливается «оболочечным» и «струйным» механизмами образования капель при выходе из жидкой фазы газов. Сконцентрированная за счет работы подъемных сил жидкости в нескомпенсированных работой сил трения пузырьках энергия претерпевает преобразование в энергию поверхностного натяжения капель, образуемых при разрыве пленки жидкости. Выражение образования капель над поверхностью жидкости возможно записать в виде
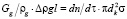
где l – характерный размер системы, ρg – плотность газа, dn / dτ – скорость образования капель, g – ускорение свободного падения, dk – диаметр капли, Gg – массовый расход газа.
Преобразуя это выражение, получим
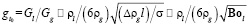 ,
,
где gt0 – масса капель в единице массы газа, Bol – критерий Бонда по параметру l. Примем, что диаметр капель dk обусловлен действием сил поверхностного натяжения:
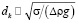 .
.
При диспергировании жидкости под воздействием возмущений со стороны барботирующих пузырьков газов, проходящих через расплав, распределение капель по размерам может быть выражено в виде доли капель, которые имели бы средние размеры меньше, чем характерный, при этом соотношение после разложения в ряд при малых диаметрах dt будет справедливым: gt ≈ gt0(dt / dш)n, где dt – диаметр витания капель, dш – средний диаметр капель после диспергирования.
Возможно предположить, что в результате выхода на поверхность барботирующих пузырьков будут образовываться обтекаемые ускоренными потоками газа цилиндрические полые пленки из пузырьков, в которых поперечные и продольные колебания пленок вызывают случайные возмущения сил трения. Названные колебания будут определять «струйный» механизм диспергирования. Между средним диаметром при генерации капель и характерным размером системы существует обратно пропорциональная критерию Вебера We взаимосвязь. Возможно приближенно получить из следующего соотношения
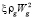 = 8σ/dш,
= 8σ/dш,
dш / δ = 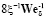 .
.
Из баланса сил сопротивления и веса тела возможно определить диаметр витания:
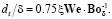
Согласно уравнению (5) получим, что режим химического реагирования сказывается на транспорте жидкой фазы из зоны реакции, в основном за счет увеличения скорости газа. Режим работы реакционной зоны зависит от газосодержания, т.е. от количества газовой фазы, температуры, выделяемой мощности, и увеличивает интенсивность процесса образования капель.
Химический состав пыли меняется по ходу прохождения газового тракта в связи с тем, что частицы пыли являются центрами конденсации для возгонов. На долю транспортируемой жидкости влияет состав жидкой фазы, определяя коэффициент поверхностного натяжения. Если обобщить зависимость уноса капель для различных типов технологических реакторов от критерия Вебера, как режимного параметра, можем записать
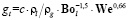 .
.
Заключение
Изложенное позволяет сделать вывод, что образование шлама в реакционной зоне печи может регулироваться изменениями режимов, а на их карты целесообразно добавлять линии уровня зависимости потоков с целью учета ухудшения качества продукта, вызванного сопутствующим образованием пыли.
Математическое описание процессов на основании проведенных исследований, протекающих в реакционной зоне рудно-термической печи, может использоваться на следующих этапах проведения изысканий по созданию алгоритмов и методов обеспечивающих повышение энерго- и ресурсоэффективности, техногенной и экологической безопасности, с учетом способов электротермической переработки рудного фосфатного сырья и многостадийного процесса образования шлама, позволяющий учитывать количественные и качественные параметры шихты.
Разработаны использующие гидродинамический подход математические модели, которые позволяют описать процессы шламообразования при термической переработке фосфатного рудного сырья в рудно-термических печах. Проведена валидация результатов проведенных вычислительных экспериментов с натурными, которая позволяет сделать выводы о корректности представленных математических моделей и возможности их использования для всестороннего описания химико-технологических процессов, протекающих в плавильном оборудовании, а также поиске и анализе возможностей рационального использования сырьевых и топливных ресурсов для производства фосфора термическим способом. Предложенные математические модели учитывают теплогидравлические особенности процессов переработки рудного фосфатного сырья, в приближении сосредоточенных параметров описывая процесс образования шлама, который характеризуется явлением уноса шламовых частиц пузырьками барботирующих расплав газов и загрязнением фосфора-сырца на выходе из печи этими частицами.
Таким образом, математическое моделирование энергоемких химико-технологических процессов дает возможность глубже понимать разнообразные взаимосвязанные температурно-зависимые превращения сырья и выбирать наиболее рациональные подходы к расходованию ресурсов при выборе наиболее энергоэффективных режимов работы оборудования.
Библиографическая ссылка
Орехов В.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ОБРАЗОВАНИЯ ШЛАМА В РУДНО-ТЕРМИЧЕСКИХ ПЕЧАХ ПРИ ПЕРЕРАБОТКЕ ФОСФАТНОГО РУДНОГО СЫРЬЯ // Современные наукоемкие технологии. 2023. № 7. С. 78-86;URL: https://top-technologies.ru/ru/article/view?id=39698 (дата обращения: 01.03.2026).
DOI: https://doi.org/10.17513/snt.39698



