Устойчивость популяций является важным аспектом защиты природы, а в случае промысловых видов имеет также большое экономическое значение. Задача оптимизации интенсивности промысла достаточно изучена [1–3]. Авторы [2] отмечают проблему избыточной ловли рыбы с превышением оптимальных значений в Средиземном море. Решение проблемы позволит поддерживать биоразнообразие. Моделирование промысла в экосистеме, содержащей потенциально вредный вид и взаимодействие вида хищник – жертва, описано в работе [4]. Как отмечают авторы, в такой биосистеме повышение плотности динофлагеллятного фитопланктона может привести к существенному вреду здоровью и экономическим последствиям, поэтому такие экосистемы следует контролировать с особой бдительностью. Следует отметить важность обеспечения экологической устойчивости для человечества [5]. Рост численности человечества и уровня потребления приводит к повышению антропогенной нагрузки на природную среду, что сводится к исчерпанию природных ресурсов и загрязнению.
Для сохранения уровня жизни человечества необходимо повышать эффективность использования природных ресурсов. Эта задача сводится к обеспечению параметров промысла, обеспечивающего максимизацию прибыли при сохранении устойчивости популяции. Такой режим соответствует случаю полностью контролируемого промысла, реализуемого при плановой экономике или частной собственности на место обитания популяции. В условиях рыночной экономики обеспечение оптимального объема промысла может регулироваться путем введения экологических налогов [6, 7]. Регулирование налогообложения на основе модели динамики популяции в аграрной стране рассматривается в работе [8]. Рассматриваются два варианта: небольшое население, облагаемое налогом по высокой ставке, нестабильное к небольшим колебаниям, или большее население, облагаемое налогом по более низкой ставке, которая является стабильной. Данная задача с точки зрения динамики системы аналогична задаче об оптимизации промысла. Возникновение и поддержание циклических процессов в экономике рассмотрено в работе [9]. В данной работе рассмотрены циклы в различных условиях. Ключевым фактором цикличности является задержка в реакции системы на изменяющиеся условия, например постепенное нарастание дефицита ресурса по мере его чрезмерного использования.
Целью исследования является использование подхода, основанного на анализе нелинейной динамической системы, включающей в себя взаимосвязи динамики популяции с учетом внешних воздействий. Выход за пределы статистического подхода, предложенного в [9], позволяет различать естественную динамику управляемого объекта и результат влияния на него решений, принимаемых на более высоком уровне [10]. Под метаоптимизацией понимается многоуровневая оптимизация [11]. Взаимосвязь двух смежных уровней заключается в том, что управляемые переменные на верхнем уровне являются параметрами на нижнем уровне. В результате этого каждое вычисление целевой функции на верхнем уровне требует решения задачи оптимизации на нижнем уровне. При увеличении количества уровней требуется существенно больший объем вычислений, особенно в случае невыпуклости на некоторых уровнях.
Постановка задачи и ее анализ
Рассмотрим модельную экосистему, в которой существует один промысловый вид. Его популяция определяется дифференциальным уравнением
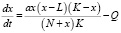, (1)
где x(t) – популяция, a – коэффициент роста популяции без учета внутривидовой конкуренции и негативного влияния малой плотности на скорость размножения, L – критический размер популяции, K – равновесный размер популяции в отсутствие промысла, N – характерный размер популяции, β – интенсивность промысла, Q = xβ – объем промысла,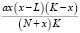 
– естественный прирост популяции,
Равновесная популяция имеет место при интенсивности промысла, определяемой соотношением
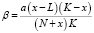. (2)
Для формулирования задачи оптимизации рассмотрим экономический аспект промысла. В отличие от работы [4, 12], эластичность спроса по цене на продукт промысла при количественном анализе не учитывается. Расходы на промысел определяются соотношением C = dβ + βxT, где d – расходы на единицу интенсивности промысла с учетом равновесной нормы прибыли и всех обязательных налогов и сборов, не связанных с объемом улова; T – косвенный налог на единицу улова, который оптимизируется в данной работе. Доход от промысла определяется соотношением R = Pxβ, где P – доход от продажи единицы улова с учетом только прямых налогов, величина которых связана с размером улова. Таким образом, экономическая прибыль от промысла равна
V = R – C = Pxβ – dβ – βxT. (3)
Рассмотрим три задачи оптимизации, соответствующие следующим условиям:
1. Весь промысел в экосистеме контролируется его собственником. На рынке существует много участников, каждый из которых не влияет на цену единицы улова.
2. Промысел бесконтрольный, и любой желающий может участвовать в нем, влияние каждого отдельного участника на динамику популяции пренебрежимо мало.
3. Промысел регулируется введением налога на единицу улова, и любой желающий может участвовать в промысле. Влияние каждого отдельного участника промысла на популяцию пренебрежимо мало.
Основные предположения: отсутствует несанкционированный промысел; погрешность параметров, связанных с популяцией и экономикой, а также влияние такой погрешности на устойчивость системы рассматривается только в форме воздействия малых возмущений на систему; время реакции участников промысла на изменение экономических условий не учитывается; динамика перехода между режимами не рассматривается, а учитывается только наличие и устойчивость стационарных режимов экосистемы и промысла.
Первая задача сводится к максимизации экономической прибыли за счет изменения интенсивности промысла α при отсутствии косвенного налога (T = 0): V → max и β ≥ 0, при котором существует устойчивое стационарное состояние популяции.
Согласно условиям второй задачи, каждый участник промысла принимает решение самостоятельно. Таким образом, если при данной интенсивности промысла V / β > 0, экономическая прибыль на единицу промысла положительная, то его интенсивность увеличивается, а при V / β < 0 уменьшается. В случае нулевой интенсивности промысел может возобновиться при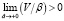 
. Отсутствие промысла не способствует убыли популяции и, как следствие, не несет риска устойчивости экосистеме, поэтому данный случай далее не рассматривается. Таким образом, задача сводится к поиску решений вида
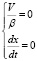. (4)
В третьей задаче рассматривается метаоптимизация регулирования косвенного налога на единицу улова, и она сводится к двухуровневой задаче оптимизации. На нижнем уровне выполняется моделирование оптимального поведения промысловиков, аналогичное второй задаче без предположения о нулевом значении косвенного налога. На верхнем уровне выполняется оптимизация величины косвенного налога с учетом его влияния на оптимальность действия промысловиков. Основное ограничение при регулировании – обеспечение устойчивости экосистемы, то есть обеспечение равновесной популяции не меньше L. В качестве целевой функции можно рассмотреть максимизацию суммы экономической прибыли и собранного налога. Так как экономическая прибыль промысловиков равна нулю в равновесных условиях, целевая функция примет вид F = Tβx.
Результаты исследования и их обсуждение
Для решения всех трех задач необходимо найти стационарные состояния системы, описанной уравнением (1), и проверить их устойчивость, для этого запишем уравнение
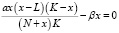, (5)
x = 0 – является одним из корней. Данный режим соответствует полному вымиранию популяции и поэтому не считается приемлемым с практической точки зрения.
Решая уравнение относительно x, получаем
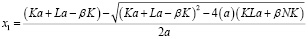, (6)
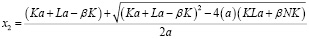. (7)
Устойчивому режиму равновесия соответствует решение (7) при условии, что оно отличается от (6). В качестве критерия устойчивости рассмотрим условие положительности дискриминанта уравнения (6) относительно переменной β. Запишем экономическую прибыль как функцию от равновесной популяции x и известных параметров, предполагая, что интенсивность промысла соответствует всему естественному приросту популяции, а косвенный налог отсутствует V = R – C = Pxβ – dβ, а с учетом (5), получим зависимость интенсивности промысла как функции популяции:
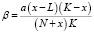. (8)
Величина промысла должна быть неотрицательна, поэтому получим ограничения x ≥ L, x ≤ K, которые соответствуют условию неуменьшения популяции в отсутствие промысла, причем x = L – неустойчивое состояние равновесия. Путем алгебраических преобразований (2), (3) и (8), при отсутствии косвенного налога, получим зависимость экономической прибыли от равновесной популяции
.
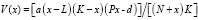Учитывая указанные ранее ограничения, получение экономической прибыли возможно, если размер популяции удовлетворяет условию (Px – d) > 0. Достижимость этого условия в популяции имеет место, если PK > d. Это значит, что затраты на промысел меньше стоимости улова при максимальной популяции. Устойчивость экосистемы определяется возможностью уменьшения популяции ниже критического значения L, при котором убыль имеет место даже в отсутствие промысла и восстановление популяции возможно только мерами, не рассмотренными в данной математической модели популяции. В случае отклонения от оптимального режима промысла имеет место уменьшение прибыли, что формирует отрицательную обратную связь. Неточность в определении параметров экосистемы может быть выявлена по факту уменьшения популяции и, как следствие, улова на единицу интенсивности промысла. Вымирание популяции возможно только при критических ошибках управления промыслом или в экстремальных условиях. При наличии эластичности спроса увеличение объемов вылова уменьшает рыночную цену за единицу. С одной стороны, это снижает рост прибыли от повышения интенсивности промысла. С другой стороны, в случае снижения популяции ниже оптимального значения цена за единицу улова вырастает, что может способствовать созданию стимула к промыслу даже в критических условиях.
Для решения второй задачи выполним анализ устойчивости экосистемы при бесконтрольном промысле. В этих условиях нет единого центра принятия решений по контролю популяции с учетом эластичности спроса, поэтому цена постоянна. Целесообразность промысла определяется балансом доходов и расходов с учетом нормы прибыли (4), что приводит к соотношению x = (d/P). Таким образом, интенсивность промысла будет возрастать при популяции x > (d/P) и убывать в противном случае. Для обеспечения стационарного режима улов должен быть уравновешен естественным приростом популяции. Если для размера популяции значение естественного прироста положительное, то размер популяции будет постоянным, в противном случае будет происходить его уменьшение. В случае (d/P) < L промысел будет выгоден для участников даже при популяции ниже критического значения, до того как популяция упадет до x = (d/P), далее промысел перестанет быть экономически целесообразным, но плотность популяции будет настолько мала, что произойдет ее вымирание даже при отсутствии внешних воздействий. В реальных условиях реакция участников промысла на изменение условий происходит с некоторой задержкой, что приводит к формированию квазипериодической динамики промысла и, как следствие, является фактором неустойчивости.
Для решения третьей задачи рассмотрим принятие решений на двух уровнях. Участники промысла находятся на нижнем уровне. В данном случае равновесная популяция в результате действий промысловиков зависит от налога и определяется соотношением x = d/(P–T). Для обеспечения устойчивости экосистемы сумма налога должна быть такой, что размер равновесной популяции превосходит критическое значение L, что в результате приводит к неравенству d/(P–T) > L. Подставляя (2) в целевую функцию с учетом значения T, получаем выражение
.
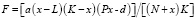Динамика популяции при оптимальном значении косвенного налога будет идентична случаю централизованного управления промыслом. Основное различие состоит в методах регулирования: вместо непосредственного планирования интенсивности промысла следует регулировать величину налога. Всю стоимость улова можно разделить на экономические издержки (включающие в себя расходы на промысел и норму прибыли) и доход от использования природных ресурсов, который получает собственник, реализующий свои права. Таким собственником может быть как частная компания, осуществляющая промысел, так и государство. Оба варианта более благоприятны, чем бесконтрольный промысел как с экономической (позволяя получать доход от природных ресурсов), так и с экологической точки зрения (обеспечивая устойчивость экосистемы).
На рисунке показана зависимость равновесного объема промысла Q, экономической прибыли от промысла V в отсутствие налога в зависимости от равновесной популяции x. Как было отмечено выше, при государственной собственности на экосистему зависимость суммы налога от равновесной популяции идентична V.
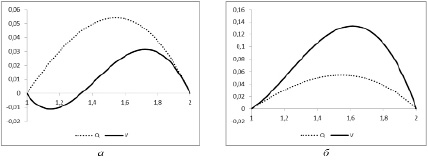
Экономические характеристики промысла при a = 1, L = 1, K = 2, N = 2, d = 3 и различных значениях цены a – P = 3, б – P = 5
Как видно из рисунка, а, при меньшей цене промысел становится экономически нецелесообразным при значениях численности популяции около критических даже в отсутствие косвенного налога, о чем свидетельствует асимптотика кривой V(x) в окрестности x = L.
В результате чего поддерживается равновесная популяция, соответствующая пересечению кривой V(x) с осью абсцисс. На рисунке, б, видно, что в отсутствие регулирования промысел остается выгодным при любом значении популяции выше критического, что без принятия мер приведет к вымиранию популяции. При контроле промысла, как прямом управлении, так и регулировании косвенным налогом [13], режим использования природных ресурсов будет соответствовать максимуму функции V(x). В окрестности x = K естественный прирост популяции замедляется ввиду внутривидовой конкуренции, что не позволяет поддерживать равновесие только при промысле малого объема. Как видно из рисунка, максимальный объем прибыли достигается при большем значении размера популяции, чем максимум объема промысла. Это связано с уменьшением требуемой интенсивности промысла и, как следствие, расходов на него при большем размере популяции. В данной работе не рассматриваются экосистемы, находящиеся внутри границ нескольких государств, в которых имеет место миграция особей [14].
Заключение
На основе поставленной задачи и использования приемов анализа динамических систем показаны преимущества регулирования промысла и возможность получения максимальной отдачи от экосистемы. Для бесконтрольного промысла популяция убывает до значений, при которых доходы промысла равны расходам на него, что нивелирует экономию промысловиков на косвенных налогах. Введение косвенного налога является практической реализацией принципа принадлежности природных ресурсов государству и его народу. В рамках предложенного подхода рациональное природопользование приводит к максимизации экономической прибыли. С точки зрения экологии данный режим можно считать оптимальным, если основная цель защиты природы состоит в долгосрочном поддержании ее состояния, благоприятном для человека.
Библиографическая ссылка
Катаева Л.Ю. О ПРОСТОМ ПОДХОДЕ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ ОПТИМИЗАЦИИ ФИСКАЛЬНЫХ ИНСТРУМЕНТОВ ДЛЯ ОБЕСПЕЧЕНИЯ УСТОЙЧИВОСТИ ПОПУЛЯЦИИ ПРОМЫСЛОВЫХ ПОРОД // Современные наукоемкие технологии. – 2023. – № 6. – С. 35-40;URL: https://top-technologies.ru/ru/article/view?id=39628 (дата обращения: 19.05.2024).