Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шульман В.Д. 1 Шабанов В.В. 1 Максименко О.Е. 2

---

1 ФГБОУ ВО «Московский государственный технический университет имени Н.Э. Баумана»

2 ФГАОУ ВО «Национальный исследовательский ядерный университет «МИФИ»

Данная статья посвящена проблеме балансировки сетевой нагрузки в контексте гетерогенных вычислительных систем. Цель исследования – разработать программную модель задачи распределения сетевой нагрузки и экспериментальным путем произвести анализ эффективности работы использованных алгоритмов. В статье анализируется литература по предмету исследования, производится синтез (гибридизация) алгоритмов, накладывается ограничение на входной поток в виде атомарности и независимости сетевых запросов, проводится экспериментальное программное моделирование и выполняется наблюдение, измерение и оценка полученных в ходе моделирования результатов. В статье рассматриваются понятия вычислительного кластера, программного комплекса и вычислительной системы, дается формальная постановка задачи балансировки нагрузки в распределенных гетерогенных вычислительных системах. В качестве результата проделанной работы выступает программная модель распределенной гетерогенной вычислительной системы, где на примере гибридизации алгоритма взвешенного кругового обхода (Weighted Round Robin) и стандартного трехкомпонентного генетического алгоритма был промоделирован процесс адаптивной балансировки нагрузки. Научная новизна заключается в предложении авторского подхода при решении проблемы адаптивной балансировки в контексте гетерогенных вычислительных систем. В ходе эксперимента была продемонстрирована эффективность используемого гибридного подхода, которая заключается в сокращении среднего времени обработки сетевых запросов, поступающих в систему.

Статья в формате PDF

375 KB

вычислительная система

сетевой запрос

алгоритм балансировки

генетический алгоритм

целевая функция

агент

1. Малявко А.А., Менжулин С.А. Суперкомпьютеры и системы. Построение вычислительных кластеров: учебное пособие. Новосибирск: Издательство НГТУ, 2018. 96 c.

2. Емельянов А. Балансировка нагрузки: основные алгоритмы и методы // Habr [Электронный ресурс]. URL: https://habr.com/ru/company/selectel/blog/250201 (дата обращения: 18.02.2023).

3. Krzywda J. [и др.]. Power-performance tradeoffs in data center servers: DVFS, CPU pinning, horizontal, and vertical scaling // Future Generation Computer Systems. 2018. № November (81). C. 114–128.

4. Спиряев О. Вертикальное и горизонтальное масштабирование систем // BYTE [Электронный ресурс]. URL: https://www.bytemag.ru/articles/detail.php?ID=6670 (дата обращения: 26.02.2023).

5. Технологии микроэлектроники на пальцах : «закона Мура», маркетинговые ходы и почему нанометры нынче не те // Habr [Электронный ресурс]. URL: https://habr.com/ru/post/453438 (дата обращения: 11.03.2023).

6. Шульман В.Д., Волхонцева П.Д., Максименко О.Е. Перспективы экстенсивного роста производительности вычислительных кластеров // Вопросы устойчивого развития общества. 2022. № 2. C. 293–298.

7. Тамбовцев А.Ю., Смольянов А.Г. О практических аспектах создания приложений микросервисной архитектуры совместно с распределенным программным брокером сообщений Apache Kafka // XXI век: итоги прошлого и проблемы настоящего плюс. 2021. № 53 (1). C. 31–34.

8. Li D.C., Wu C., Chang F.M. Determination of the parameters in the dynamic weighted Round-Robin method for network load balancing. Computers and Operations Research. 2005. № 8 (32). C. 2129–2145.

9. Аверченков В.И., Казаков П.В. Эволюционное моделирование и его применение. М.: Флинта, 2016. 200 c.

10. Zadeh L.A. Soft Computing and Fuzzy Logic. IEEE Software. 1994. No. 6 (11). P. 48–56.

11. Тенев В.А. Решение задачи многокритериальной оптимизации генетическими алгоритмами // Интеллектуальные системы в производстве. 2006. № 8 (2). C. 103–109.

12. Панченко Т.В. Генетические алгоритмы. 2007. 1–86 c.

13. Покусин Н.В. Балансировка нагрузки распределенной гетерогенной вычислительной системы в условиях априорной неопределенности о характере входного потока заявок // Вестник евразийской науки. 2013. № 925 (7). C. 1–7.

14. Коськин А.В., Митин А.А., Артемов А.В. Концепция построения интеллектуальной системы с выбором методов и средств анализа данных для обработки информации // Информационные технологии в науке, образовании и производстве (ИТНОП-2018) : VII Международная научно-техническая конференция: сборник трудов конференции (Белгород, 17–19 октября 2018 г.). Белгород: ООО ГиК, 2018. C. 433–437.

15. Шульман В.Д., Дегтяренко А.С. Построение клеточных автоматов с помощью 3-операторных генетических алгоритмов // Вестник Коломенского института (филиала) Московского политехнического университета : сборник научных трудов. 2021. C. 318–329.

Современные вычислительные системы – это множества вычислительных узлов, объединенных сетью и функционирующих как единое целое. Вычислительные системы могут быть как однородными (состоять из идентичных узлов), так и неоднородными (состоять из узлов различной конфигурации и, как следствие, узлов разных мощностей) [1].

Одна из основных задач, решаемых в рамках эксплуатации вычислительной системы, – это распределение нагрузки между ее узлами. Нагрузка между узлами балансируется при помощи набора специальных методов. Эффективность работы системы напрямую зависит от того, насколько оптимально осуществляется такое распределение [2].

Балансировка нагрузки может осуществляться при помощи как аппаратных, так и программных инструментов. Технологии балансировки нагрузки активно развиваются и представляют сейчас большой интерес с точки зрения IT-отрасли.

Цель исследования – разработать программную модель задачи распределения сетевой нагрузки и экспериментальным путем произвести анализ эффективности работы использованных алгоритмов.

Материалы и методы исследования

Рассматриваемыми объектами являются распределенные вычислительные системы, алгоритм балансировки нагрузки и генетический алгоритм как метод оптимизации.

В процессе работы была исследована предметная область вычислительных систем и балансировки нагрузки. Были проанализированы характеристики алгоритмов балансировки сетевой нагрузки, их особенности и решаемые ими задачи.

В работе использовался метод программного моделирования. Разработанная программная модель демонстрирует принцип гибкой балансировки нагрузки, который заключается в адаптации под меняющуюся среду функционирования вычислительной системы и равномерном распределении сетевых запросов по узлам в соответствии с доступными ресурсами.

Для реализации модели был использован гибридный подход на базе алгоритма балансировки Round Robin и генетического алгоритма.

В области информационных технологий распространены понятия вертикального и горизонтального масштабирования. Они применяются как к физическим ресурсам, так и к программным системам, которые на них эксплуатируются [3, 4]. Закон Мура утратил свою актуальность [5], что делает горизонтальное масштабирование систем более предпочтительным [6], а проблему балансировки нагрузки более актуальной.

Балансировка нагрузки осуществляется при помощи комплекса подходов и методов, которые соответствуют уровням модели OSI: сетевому, транспортному и прикладному [2].

В случае балансировки на сетевом уровне функция распределения нагрузки осуществляется посредством IP-адресов. Подразумевается, что за один IP-адрес могут отвечать сразу несколько физических машин.

При балансировке на транспортном уровне распределение нагрузки осуществляется через прокси-серверы. В отличие от сетевого уровня, на транспортном прокси-сервер выступает в качестве посредника и может добавлять в запрос дополнительные заголовки.

Балансировщики нагрузки прикладного уровня анализируют содержимое запросов и перенаправляют их на узлы системы в зависимости от контента и типа требуемых операций. Известные примеры решений для прикладной балансировки – это Nginx и PGpool [2].

Отдельно стоит упомянуть брокеры сообщений. Они работают по обратному принципу: поставщики и потребители сами кладут и достают данные из брокера. Брокеры сообщений нашли свое применение в современных микросервисных приложениях [7], однако они не занимаются балансировкой в классическом смысле, а формируют очереди сообщений.

Существует множество различных алгоритмов балансировки нагрузки. Выбирая конкретный алгоритм, нужно исходить, во-первых, из специфики конкретного проекта, а во-вторых, из задач, которые необходимо решить. Из целей, которые могут преследоваться в рамках решения задачи балансировки, можно выделить: равномерность и детерминированность распределения, минимальное время обработки, масштабируемость.

Самый известный, часто используемый и простой алгоритм балансировки – Round Robin. Запросы последовательно передаются серверам из зацикленного списка. Данный алгоритм имеет широкое применение, в частности, в системе DNS [2]. Простота алгоритма влечет и недостатки: для эффективной работы необходимо, чтобы у каждого сервера был в наличии одинаковый набор ресурсов. В современной практике эти условия в большинстве случаев оказываются невыполнимыми [2].

Weighted Round Robin (WRR) – это улучшенная версия алгоритма Round Robin. В зависимости от производительности и мощности сервера каждому из них присваивается весовой коэффициент. Это способствует более равномерному распределению нагрузки: серверы с большим весом обрабатывают больше запросов. Для эффективной работы WRR необходимо правильно подобрать веса.

Для адаптивной балансировки веса WRR должны подбираться динамически. Концепция такого алгоритма известна и именуется Dynamic Weighted Round Robin (DWRR). Существует ряд исследований, которые предлагают вариант реализации такого алгоритма, но в них зачастую речь идет о частном решении проблемы адаптивной балансировки. Например, в исследовании [8] предлагается использование различных математических эвристик совместно с периодическим считыванием состояния всей системы (использования обратной связи в режиме реального времени), что не совсем применимо к современному web, где, ввиду распределенности систем, время передачи данных обычно многократно превышает время непосредственной обработки запросов, что не позволяет эффективно использовать метрики о нагруженности системы из-за почти мгновенного их устаревания.

В рамках проводимого исследования предлагается реализация DWRR, которая предполагает подбор весов в фоновом режиме. Этот подбор в конечном счете сводится к решению оптимизационной задачи. Для решения такого класса задач существует множество методов, один из которых – метод эволюционного моделирования.

Эволюционное моделирование (ЭМ) – это стохастико-эвристический метод решения оптимизационных задач, который использует понятийный аппарат популяционной генетики [9] и идею «мягких вычислений» [10]. ЭМ применяется для решения следующих задач:

− наделение систем свойствами адаптивности и самоорганизации;

− автоматизация решения оптимизационных задач в различных областях науки;

− экспериментальное моделирование и изучение отдельных процессов.

Особое место в ЭМ занимает генетический алгоритм (ГА). Во время работы ГА выполняется параллельный анализ разных областей пространств решений. В отличие от машинного обучения, в ГА используется абсолютное значение целевой функции (ЦФ), а не ее приращение. Процесс поиска может продолжаться до тех пор, пока не будут рассмотрены все точки исследуемого пространства. В качестве ограничения могут использоваться критерии оптимума, лимит количества поколений, порог приращения ЦФ и т.д. [11].

Генетический алгоритм обладает рядом достоинств:

− независимость от вида функций;

− независимость от области определения и типов переменных;

− использование для решения широкого круга задач без нужды в изменениях.

Для получения очередного набора решений в ГА применяются операторы [9]. По-другому их еще называют этапами, так как они выполняются последовательно на каждой итерации. В стандартном ГА используются следующие операторы:

− оператор отбора (селекции);

− оператор кроссинговера (рекомбинации генов);

− оператор мутации или инверсии.

Наибольший интерес здесь представляет оператор отбора. Он используется для определения на основе fitness-функции кандидатов, гены которых будут использоваться для формирования следующего поколения. Существует множество схем отбора и их модификаций. Наиболее известные из них: отбор усечением (truncation selection), элитарный отбор (elite selection), отбор вытеснением (exclusion selection), метод Больцмана (Bolzman selection) [12].

Результаты исследования и их обсуждение

В рамках исследования была реализована программная модель распределенной гетерогенной вычислительной системы, при этом на входной поток было наложено ограничение в виде атомарности и независимости сетевых запросов. Данные ограничения позволили полностью сконцентрироваться на предмете исследования без необходимости дополнительно прорабатывать решение проблемы неопределенного характера входного потока вычислительных задач [13].

Пусть узлы вычислительной системы представляют собой множество P = {P1,…,Pn}. Узлы взаимосвязаны друг с другом и располагают некоторыми конфигурационными характеристиками, такими как ЦПУ, ОЗУ, ПЗУ и т.п.

Тогда пусть каждый Pi есть кортеж вида {p1, p2,…, pk}, элементы которого олицетворяют собой различные характеристики вычислительного узла.

Пусть имеется множество вычислительных задач X = {X1,…,Xm}, где каждый Xj есть кортеж {x1, x2,…, xk}, элементы которого олицетворяют собой различные параметры вычислительной задачи.

Также, для каждого узла Pi, с учетом его характеристик для некоторой вычислительной задачи Xj имеет место некоторое время выполнения задачи Xj на узле Pi, которое может быть формализовано в виде T = E(Pi, Xj), где E – функция, значение которой определено для каждой возможной пары Pi и Xj. Определение Pi из множества узлов системы, на котором будет выполняться вычислительная задача Xj, осуществляется функцией балансировки: Pi = B(Xj, P).

Тогда конечная задача балансировки нагрузки может быть формализована в виде минимизации суммарного времени исполнения вычислительных задач X на множестве узлов P. Для этого необходимо подобрать вид функции B:

.

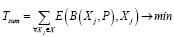Функция балансировки нагрузки B представлена алгоритмом Weighted Round Robin. Задача оптимизации, заключающаяся в подборе весовых коэффициентов для алгоритма Weighted Round Robin, была решена применением стандартного генетического алгоритма.

Таблица 1

Параметры (зависимые переменные) вычислительной задачи

Таблица 2

Характеристики (независимые переменные) вычислительной задачи

Таблица 3

Формат данных для построения множественной регрессии

Для формирования входного потока задач была разработана ML-модель предсказания характеристик вычислительной задачи по ее различным параметрам. Пример фрагмента перечня параметров вычислительной задачи, представленной изначально в виде HTTP-запроса, проиллюстрирован в табл. 1, а наиболее значимые характеристики вычислительной задачи представлены в табл. 2.

Предсказание характеристик вычислительной задачи по ее параметрам осуществляется с помощью линейной регрессии, однако, в зависимости от особенностей функционирования той или иной вычислительной системы, целесообразность использования каждой из моделей машинного обучения будет разниться от случая к случаю [14].

Таким образом, в процессе разработки модели, были реализованы три программных модуля: модуль генерации входного потока задач на базе линейной регрессии (Python) с использованием библиотеки pandas, numpy и sklearn; модуль балансировки нагрузки (Golang), включающий в себя наивную реализацию WRR; модуль настройки WRR (Golang) на базе ГА с тремя операторами (в операторе отбора используется отбор усечением, в операторе рекомбинации используется однородный кроссинговер, а в операторе мутации используется мутация вещественного приращения) [15].

Эксперимент состоял из последовательного выполнения следующих этапов:

− построение модели линейной регрессии по метрикам вычислительной системы;

− проведение процесса эволюционного моделирования;

− перенастройка алгоритма балансировки.

Пусть имеется всего три вычислительных узла (node) и два типа вычислительных задач (edp), одна количественная метрика параметра запроса (request_size) и две количественные метрики характеристики выполнения запроса (execute_time, memory_use). Тогда данные для построения модели линейной регрессии могут быть представлены табл. 3.

Показатели из этой таблицы были получены экспериментальным путем в ходе развертывания и эксплуатации простого веб-приложения на серверах облачного провайдера. Приложение состояло из трех идентичных программных модулей, запущенных на трех облачных серверах (nodes) различной конфигурации.

Таблица 4

Коэффициенты множественной линейной регрессии

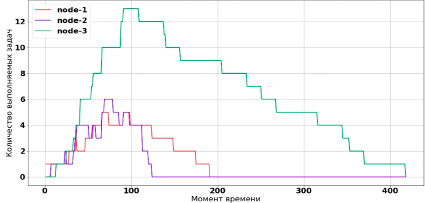
Рис. 1. Работа ненастроенного алгоритма балансировки

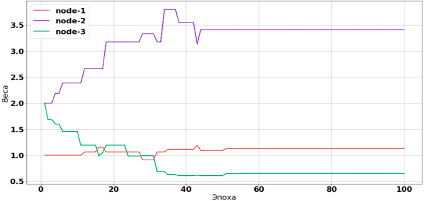
Рис. 2. Веса алгоритма балансировки

Классы node-1 и edp-1 исключены из таблицы с целью ликвидации избыточности. В результате получаем регрессионную модель с коэффициентами для каждой из зависимых переменных (табл. 4). Классы node-1 и edp-1 входят в intercept.

Работа ненастроенного алгоритма балансировки представлена на рис. 1.

Процесс работы генетического алгоритма проиллюстрирован рис. 2 и 3. На рис. 2 показано, как изменялись веса, а на рис. 3 – как менялось общее количество затрачиваемого времени на все задачи.

После завершения эволюционного процесса и установки весов на алгоритм балансировки, было получено более оптимальное распределение вычислительных задач, представленное на рис. 4.

Генерация входного потока задач производилась первые 100 с. На рис. 1 отчетливо виден дисбаланс нагрузки между узлами. Об этом также свидетельствует сильный разброс времени завершения обработки задач узлами (120, 190 и 420 с соответственно). Хуже всего себя показал узел node-3

Из рис. 2 и 3 заметно, что эволюционный процесс достиг субоптимальной ниши примерно на 50 итерации (эпохе) работы ГА. Значения весов значительно изменились. Как и ожидалось, вес узла node-3 уменьшился и стал минимальных из трех. Общее время обработки задач сократилось приблизительно на 35 % (рис. 3).

По графику на рис. 4 можно сделать вывод, что рабочие узлы системы не только завершили свою работу примерно в один момент времени, но и сделали это на 200 дискретных шагов (секунд) раньше, чем в случае ненастроенного алгоритма на рис. 1.

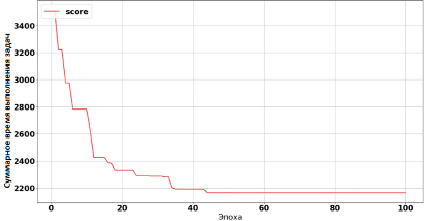
Рис. 3. Суммарное время выполнения задач на узлах

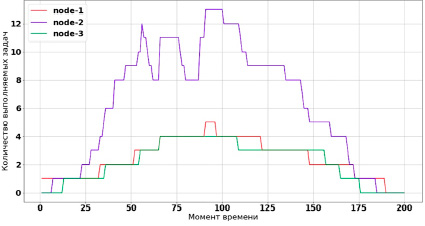
Рис. 4. Работа настроенного алгоритма балансировки

Заключение

В процессе экспериментального моделирования адаптивной балансировки нагрузки удалось добиться сокращения общего количества времени обработки задач на 35 %. Повышение эффективности балансировки было достигнуто за счет применения генетического алгоритма. Также использование этого алгоритма позволило достигнуть следующих целей балансировки: справедливость, равномерность, минимальное время обработки.

Стоит отметить, что эффективность работы представленного в данной статье метода адаптивной балансировки в значительной мере зависит от правильности (оптимальности) изначальной конфигурации весов Weighted Round Robin. На оптимальность изначальной настройки значительно влияют размер системы и гетерогенность ее программно-аппаратных средств: чем больше программно-аппаратных элементов входит в систему и чем разнообразнее эти элементы, тем тяжелее системным администраторам подобрать оптимальную конфигурацию. Программная модель, разработанная в рамках данного исследования, демонстрирует возможность решения данной проблемы посредством использования подхода адаптивной балансировки.

Разработанная программная модель имеет запас универсальности: возможно использование различных алгоритмов балансировки, произвольного количества параметров сетевого запроса, любого количества узлов с отличными друг от друга характеристиками. Однако имеют место и ограничения: сетевые запросы должны быть атомарными (не могут быть разбиты на подзапросы) и независимыми (запросы между собой не связаны отношениями порядка).

Библиографическая ссылка