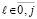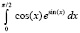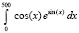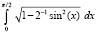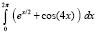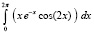В работе рассматривается компьютерное вычисление определенного интеграла от функции одной вещественной переменной на основе кусочно-интерполяционного приближения подынтегральной функции. Кусочная интерполяция выполняется с помощью интерполяционных полиномов Лагранжа и Ньютона, преобразованных в каноническую форму алгебраических полиномов с числовыми коэффициентами. Апробация подхода была представлена в [1], при этом остались нерешенными следующие проблемы. Во-первых, коэффициенты интерполяционных полиномов на каждом подынтервале пересчитывались заново по ходу каждого выполнения программы, что увеличивало трудоемкость метода. В то же время эти коэффициенты можно было записать в память и использовать в разделе констант программы инвариантно относительно вида подынтегральной функции и промежутка интегрирования. Во-вторых, возникала неточность вычисления коэффициентов полиномов степеней выше пятой вследствие погрешностей операций с плавающей точкой в языке программирования. Это приводило к ограничению набора степеней интерполяционных полиномов, избыточности числа подынтервалов и, как следствие, к ограничениям точности приближения, временной сложности метода, длины промежутков интегрирования. В целом сохранялась общая проблема нестабильности [2] вычисления интегралов по формулам Ньютона-Котеса высокого порядка, реализуемым на основе кусочной интерполяции с помощью полиномов Лагранжа и Ньютона. Ниже ставится задача устранить отмеченные недостатки подхода к реализации формул Ньютона-Котеса на предложенной основе, в частности требуется повысить точность приближения интеграла, в том числе на больших промежутках интегрирования, и стандартизировать пользовательский интерфейс программ, реализующих метод. Кроме того, ставится задача распространить метод на компьютерное приближение первообразной подынтегральной функции. Требуется выполнить численные эксперименты, описать их результаты и привести коды стандартизированных программ.
Цель работы заключается в минимизации погрешности и временной сложности кусочно-интерполяционного вычисления интегралов, а также в стандартизации программ, реализующих метод на основе полиномов Лагранжа и Ньютона. Требуется выполнить математическое обоснование предложенного метода и дать экспериментальное подтверждение его эффективности в рассматриваемых аспектах.
Исходные соотношения. В основе дальнейших интегральных преобразований лежит алгоритм восстановления коэффициентов полинома по его корням. С помощью этого алгоритма преобразуются компоненты полинома, интерполирующего подынтегральную функцию, затем приводятся подобные. В результате интерполяционный полином принимает форму алгебраического полинома с числовыми коэффициентами, что автоматически влечет первообразную от него и упрощает вычисление определенного интеграла. Пусть
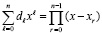 . (1)
. (1)
Если 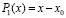 , то
, то 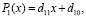 где
где 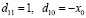 .
.
Если уже вычислены коэффициенты полинома
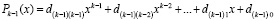 ,
, 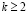 ,
,
то 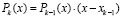 .
.
Приравнивание коэффициентов при одинаковых степенях влечет
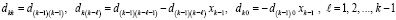 . (2)
. (2)
При 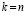 значения левых частей равенств (2) совпадут с искомыми значениями коэффициентов полинома (1). В матричной форме (2) можно записать в виде
значения левых частей равенств (2) совпадут с искомыми значениями коэффициентов полинома (1). В матричной форме (2) можно записать в виде
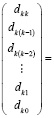
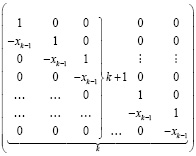
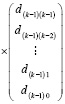 .
.
Отсюда следует выражение коэффициентов полинома через его корни [1; 3]
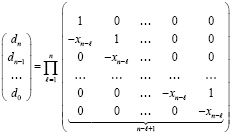 ,
,
Представленное восстановление коэффициентов полинома по его корням алгоритмически отличается от формул Виета [4] и не использует уравнения Ньютона для симметрических функций корней [4]. Алгоритм (2) следующим образом применяется к интерполяционному полиному Лагранжа. Для интерполяции функции 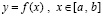 полином Лагранжа можно записать в виде
полином Лагранжа можно записать в виде
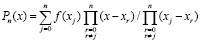 , (3)
, (3)
где xr – узлы интерполяции. По алгоритму (2) можно вычислить коэффициенты полинома 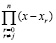 , затем привести подобные. Непосредственно ниже этот подход применяется для случая равноотстоящих узлов интерполяции.
, затем привести подобные. Непосредственно ниже этот подход применяется для случая равноотстоящих узлов интерполяции.
Пусть на отрезке 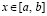 взяты равноотстоящие узлы для полинома (3):
взяты равноотстоящие узлы для полинома (3):
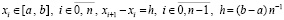 .
.
Здесь и всюду в дальнейшем предполагается, что начальный узел совпадает с левой границей отрезка, а конечный узел – с его правой границей. В этом случае 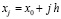 ,
, 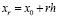 ,
, 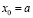 ,
, 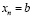 . Отсюда
. Отсюда
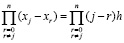 ,
, 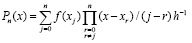 .
.
Вводится переменная 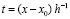 .
.
Тогда 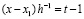 , …,
, …, 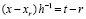 ,
, 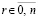 , и
, и
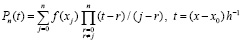 . (4)
. (4)
В отличие от аналога [5] для (4) ниже выполнен перевод числителей дробей слагаемых в форму полиномов с целочисленными коэффициентами. Как следствие, появится аналитическое выражение первообразной от интерполяционного полинома. Числитель дроби 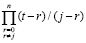 можно записать в виде
можно записать в виде
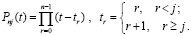 (5)
(5)
По схеме (2) получится:
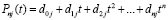 . (6)
. (6)
Коэффициенты полинома (6) – целые числа, они не зависят от интерполируемой функции, от диапазона и расположения её аргумента. Знаменатель дроби в (4) отличается от числителя тем, что в нем t = j. В результате
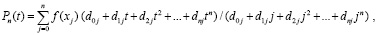 (7)
(7)
при 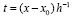 ,
,
Числитель в (7) вычисляется по схеме Горнера
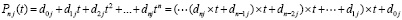 . (8)
. (8)
В этих обозначениях
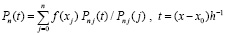 . (9)
. (9)
Если каждый коэффициент каждого из полиномов с индексом j в числителях слагаемых (9) разделить на число 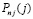 , то интерполяционный полином (7), (9) примет вид
, то интерполяционный полином (7), (9) примет вид
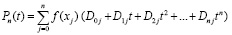 , (10)
, (10)
где
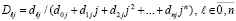 . (11)
. (11)
Коэффициенты (11) полинома (10), как и компоненты, из которых они получены, по-прежнему не зависят от вида интерполируемой функции, от отрезка интерполирования, но зависят только от степени интерполяционного полинома и номера узла интерполяции. Этим свойством будут обладать и коэффициенты первообразной полинома (10). Первообразная рассматриваемого полинома примет вид
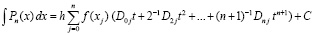 , (12)
, (12)
где 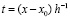 , С – произвольная постоянная.
, С – произвольная постоянная.
Приближенное вычисление интегралов на основе кусочной интерполяции с помощью полиномов Лагранжа. Пусть отрезок [a, b] разбит на малые подынтервалы равной длины с общими границами разбиения
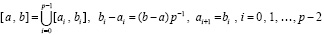 . (13)
. (13)
Рассмотренные выше построения воспроизводятся на каждом подынтервале 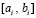 в отдельности,
в отдельности, 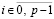 , соответственный полином, его узлы и коэффициенты отмечаются индексом i, для отличия от обозначения других полиномов в обозначение полинома Лагранжа добавляется первая буква фамилии Лагранжа. Полином (10), (11) примет вид
, соответственный полином, его узлы и коэффициенты отмечаются индексом i, для отличия от обозначения других полиномов в обозначение полинома Лагранжа добавляется первая буква фамилии Лагранжа. Полином (10), (11) примет вид
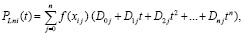
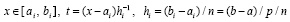 . (14)
. (14)
Одинаковый на всех подынтервалах шаг интерполяции ниже обозначен
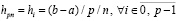 .
.
Непосредственно из (12), (13), (14) вытекают формулы приближенного вычисления интегралов:
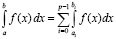 ,
, 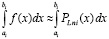 ,
,
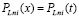 ,
,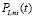 определяется из (14).
определяется из (14).
С введенным обозначением шага интерполяции
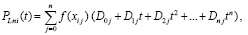
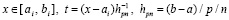 . (15)
. (15)
Из (12) с заменой переменной 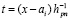 и из (15) следует
и из (15) следует
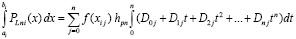 .
.
Взятие первообразной влечет
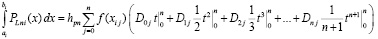 ,
,
или, в результате выполнения подстановки,
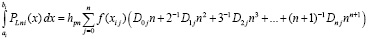 . (16)
. (16)
Сложение (16) по всем подынтервалам дает формулу приближенного вычисления интеграла:
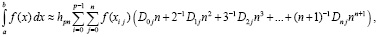 (17)
(17)
при 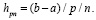
Как отмечалось, выражение в скобках внутренней суммы в (17) является числом, зависящим от степени интерполяционного полинома и от номера узла интерполяции, но не зависящим от номера подынтервала и вида подынтегральной функции. Ниже это число обозначается
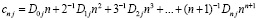 . (18)
. (18)
Коэффициенты 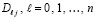 , получаются переходом от (5) к (6) в соотношении (4) с использованием (2). Значения (18) могут быть вычислены априори, записаны в память компьютера, быть хранимыми константами и применяться для приближенного вычисления интеграла от любой функции. В частности, их можно сохранять в разделе описаний констант программы и непосредственно использовать в разделе инструкций этой программы при вычислении интегралов вида (17).
, получаются переходом от (5) к (6) в соотношении (4) с использованием (2). Значения (18) могут быть вычислены априори, записаны в память компьютера, быть хранимыми константами и применяться для приближенного вычисления интеграла от любой функции. В частности, их можно сохранять в разделе описаний констант программы и непосредственно использовать в разделе инструкций этой программы при вычислении интегралов вида (17).
Из изложенного вытекает
Теорема 1. На основе кусочной интерполяции подынтегральной функции с помощью полиномов Лагранжа значение интеграла приближенно вычисляется из соотношения
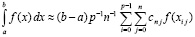 , (19)
, (19)
где 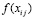 – значение подынтегральной функции в j-м узле интерполяции на i-м подынтервале из (13), коэффициенты и числовые параметры определяются из (17), (18).
– значение подынтегральной функции в j-м узле интерполяции на i-м подынтервале из (13), коэффициенты и числовые параметры определяются из (17), (18).
Ниже приводится таблица значений коэффициентов (18) (поделенных на n) для различных степеней интерполяционных полиномов Лагранжа.
Замечание 1. В Delphi значения коэффициентов, начиная с полиномов степени n = 5, в формате extended вычисляются с погрешностью, этим объясняются ограничения степеней полиномов Лагранжа при вычислении интегралов на основе кусочной интерполяции по программам, представленным в [1]. Для повышения точности вычислений при составлении табл. 1 использовался язык Python с модулем decimal.
Таблица 1
Значения коэффициентов cnj / n приближения интеграла (19) для различных степеней n полинома Лагранжа
|
n |
cnj / n, |
|
1 |
(0.500000000000000000000, 0.500000000000000000000) |
|
2 |
(0.166666666666666666667, 0.666666666666666666667, 0.166666666666666666667) |
|
3 |
(0.125000000000000000000, 0.375000000000000000000, 0.375000000000000000000, 0.125000000000000000000) |
|
4 |
(0.077777777777777777778, 0.355555555555555555556, 0.133333333333333333333, 0.355555555555555555556, 0.077777777777777777778) |
|
5 |
(0.065972222222222222222, 0.260416666666666666667, 0.173611111111111111111, 0.173611111111111111111, 0.260416666666666666667, 0.065972222222222222222) |
|
6 |
(0.048809523809523809524, 0.257142857142857142857, 0.032142857142857142857, 0.323809523809523809524, 0.032142857142857142857, 0.257142857142857142857, 0.048809523809523809524) |
|
7 |
(0.043460648148148148148, 0.207002314814814814815, 0.076562500000000000000, 0.172974537037037037037, 0.172974537037037037037, 0.076562500000000000000, 0.207002314814814814815, 0.043460648148148148148) |
|
8 |
(0.034885361552028218695, 0.207689594356261022928, -0.032733686067019400353, 0.370229276895943562610, -0.160141093474426807760, 0.370229276895943562610, -0.032733686067019400353, 0.207689594356261022928, 0.034885361552028218695) |
|
9 |
(0.031886160714285714286, 0.175680803571428571429, 0.012053571428571428571, 0.215892857142857142857, 0.064486607142857142857, 0.064486607142857142857, 0.215892857142857142857, 0.012053571428571428571, 0.175680803571428571429, 0.031886160714285714286) |
|
10 |
(0.026834148361926139704, 0.177535941424830313719, -0.081043570626903960237, 0.454946288279621612955, -0.435155122655122655123, 0.713764630431297097963, -0.435155122655122655123, 0.454946288279621612955, -0.081043570626903960237, 0.177535941424830313719, 0.026834148361926139704) |
Равенство коэффициентов cnj и cn(n–j), наблюдаемое в табл. 1, является общим свойством приближения (19), которое коррелируется с известной симметрией коэффициентов формул Ньютона-Котеса [2; 6], выполненных на основе полиномов Лагранжа.
Замечание 2. В компьютерной реализации вычисления интеграла из (19) подынтервалы (13) в суммарном объединении могут не поместиться в точности в заданный промежуток интегрирования [a, b]: b – a не обязательно делится нацело на bi – ai. Целесообразно сначала вычислить интеграл на 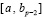 (
(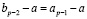 нацело делится на bi – ai), исключив последний подынтервал. Затем на последнем (исключенном) подынтервале
нацело делится на bi – ai), исключив последний подынтервал. Затем на последнем (исключенном) подынтервале 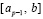 с реальным значением b отдельно провести вычисление интеграла из (16), заменив hpn на соответственный шаг интерполяции
с реальным значением b отдельно провести вычисление интеграла из (16), заменив hpn на соответственный шаг интерполяции 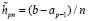 . Получится
. Получится
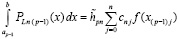 , (20)
, (20)
cnj по-прежнему из (18). Значение (20) складывается с интегралом по промежутку [a, bp–2], что дает окончательное приближение интеграла на [a, b].
При данной коррекции на последнем подынтервале начальные и конечные узлы интерполяции в точности совпадут с его границами, и удастся избежать часто возникающей погрешности компьютерной реализации квадратурных формул [1].
Программная реализация кусочно-интерполяционного вычисления интеграла на основе полиномов Лагранжа, соотношений (17) – (19) и коэффициентов из табл. 1 приводится непосредственно ниже (здесь и в дальнейшем Delphi 9 или Delphi 10).
program PIL_integral_n1_10; {$APPTYPE CONSOLE} uses SysUtils; var a,b,S:extended; n:byte; p:int64;
function f(x:extended):extended;
begin f:=cos(x)*exp(sin(x)){cos(x)}{sqrt(1-0.5*sqr(sin(x)))}{exp(x/2)+cos(4*x)}{x*exp(-x)*cos(2*x)} end;
function exact_int(a,b:extended):extended;
begin exact_int:=exp(sin(b))-exp(sin(a)){sin(b)-sin(a)}{1.35064388104767550252}{2*(exp(Pi)-1)}
{1/25*(exp(-2*Pi)*(3-10*Pi)-3)} end;
function PIL_int(a,b:extended; n:byte; p:int64):extended;
const c:array [1..10, 0..5] of extended =((0.5, 0, 0, 0, 0, 0), (0.166666666666666666667,
0.666666666666666666667, 0, 0, 0, 0), (0.125, 0.375, 0, 0, 0, 0), (0.077777777777777777778,
0.355555555555555555556, 0.133333333333333333333, 0, 0, 0), (0.065972222222222222222,
0.260416666666666666667, 0.173611111111111111111, 0, 0, 0),
(0.048809523809523809524, 0.257142857142857142857, 0.032142857142857142857,
0.323809523809523809524, 0, 0), (0.043460648148148148148, 0.207002314814814814815, 0.0765625,
0.172974537037037037037, 0, 0), (0.034885361552028218695, 0.207689594356261022928,
-0.032733686067019400353, 0.370229276895943562610,
-0.160141093474426807760, 0), (0.031886160714285714286, 0.175680803571428571429,
0.012053571428571428571, 0.215892857142857142857, 0.064486607142857142857, 0),
(0.026834148361926139704, 0.177535941424830313719, -0.081043570626903960237,
0.454946288279621612955, -0.435155122655122655123, 0.713764630431297097963));
type coeffs = array[0..5] of extended; x_arr = array[0..10] of extended;
var ai,hp,hpn,s1,s2:extended; j:byte;i:int64; s2_arr:coeffs; x:x_arr;
begin hp:=(b-a)/p; hpn:=hp/n; s1:=0; ai:=a; i:=0; for j:=1 to n div 2 do s2_arr[j]:=0;
repeat
for j:=1 to n do x[j]:=ai+j*hpn; for j:=1 to n div 2 – 1 do s2_arr[j]:=s2_arr[j]+f(x[j])+f(x[n-j]);
if n mod 2 <>0 then s2_arr[n div 2]:=s2_arr[n div 2]+f(x[n div 2])+f(x[n div 2 +1])
else s2_arr[n div 2]:=s2_arr[n div 2]+f(x[n div 2]); if i < p-1 then s1:=s1+f(x[n]);
inc(i); ai:=a+i*hp;
until i = p;
s2:=0; for j:=1 to n div 2 do s2:=s2+c[n,j]*s2_arr[j]; s1:=c[n,0]*(f(a)+2*s1+f(b)); PIL_int:=(s1+s2)*hp;
end;
begin
a:=0; b:=Pi/2; n:=10; p:=16; S:=PIL_int(a, b, n, p); writeln(‘S=’,S,’ Pogr=’,abs(S-exact_int(a,b))); readln;
end.
Результаты численного эксперимента на основе работы программы PIL_integral_n1_10 приведены в табл. 2.
Таблица 2
Значения параметров и погрешности вычисления интегралов по результатам численного эксперимента
|
Интеграл |
Приближение интеграла |
Абсолютная погрешность приближения |
Параметры программы |
|
|
1.71828182845905E+0000 |
0.00000000000000E+0000 |
n = 5, p = 512 |
|
|
-3.73603552314934E-0001 |
5.42101086242752E-0020 |
n = 9, p = 4096 |
|
|
1.00000000000000E+0000 |
0.00000000000000E+0000 |
n = 6, p = 32 |
|
|
1.35064388104768E+0000 |
0.00000000000000E+0000 |
n = 2, p = 64 |
|
|
4.42813852655585E+0001 |
0.00000000000000E+0000 |
n = 5, p = 1024 |
|
|
-1.22122604618968E-0001 |
0.00000000000000E+0000 |
n = 7, p = 4096 |
Во втором столбце табл. 1 – вычисленное программой PIL_integral_n1_10 приближенное значение интеграла из первого столбца той же строки, в третьем столбце – абсолютная погрешность приближения, в четвертом – параметры программы. Для полного эллиптического интеграла второго рода 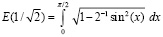 в качестве эталонного значения для сравнения принято значение
в качестве эталонного значения для сравнения принято значение 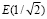 , представленное в [7].
, представленное в [7].
Вычисление интеграла из (19), включая возможное уточнение (20), обладает естественным параллелизмом. Для одновременного выполнения всех умножений вида 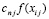 за время ty одного бинарного умножения потребуется
за время ty одного бинарного умножения потребуется 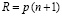 процессорных элементов (ПЭ). Сумма парных произведений вычисляется по схеме сдваивания [8], что потребует
процессорных элементов (ПЭ). Сумма парных произведений вычисляется по схеме сдваивания [8], что потребует 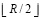 ПЭ и займет время
ПЭ и займет время 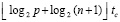 , tc – время одного бинарного сложения. Здесь и ниже β обозначает число, ближайшее целое к β не меньшее β. Требуется еще умножение полученной суммы на hpn. Вычисление шага
, tc – время одного бинарного сложения. Здесь и ниже β обозначает число, ближайшее целое к β не меньшее β. Требуется еще умножение полученной суммы на hpn. Вычисление шага 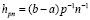 можно выполнить по ходу схемы сдваивания. В результате временная сложность T(R) параллельного вычисления интеграла составит
можно выполнить по ходу схемы сдваивания. В результате временная сложность T(R) параллельного вычисления интеграла составит
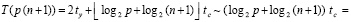
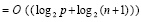 . (21)
. (21)
При ограничении степени полинома, 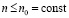 , –
, –
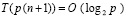 .
.
Вычисление интеграла на основе первообразной от непрерывного кусочно-интерполяцинного приближения подынтегральной функции. Пусть на отрезке (13) выполнено приближение (15) подынтегральной функции,
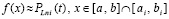 .
.
Номер подынтервала, при котором 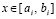 ,
, 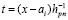 ,
, 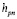 из (17), дает формула [1]
из (17), дает формула [1]
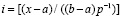 ,
,
[α] – целая часть числа α. Пусть функция f(x) непрерывна 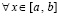 из (13), тогда она интегрируема, ее первообразная
из (13), тогда она интегрируема, ее первообразная
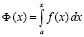 (22)
(22)
непрерывна на [a, b] [9]. Приближение подынтегральной функции, обозначаемое 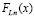 , рассматривается как самостоятельная функция, определенная на всем [a, b],
, рассматривается как самостоятельная функция, определенная на всем [a, b],
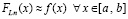 ,
,
при этом определяющими являются соотношения:
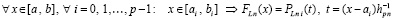 , (23)
, (23)
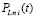 из (15).
из (15).
Начальный и конечный узел интерполяции полинома (15) всегда находятся соответственно на левой и правой границе подынтервала, поэтому при i = 0, 1, ... , p – 2
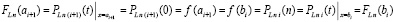 . (24)
. (24)
Согласно (15), (23), (24) функция 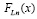 непрерывна
непрерывна 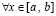 , следовательно, интегрируема на [a, b]. Ее первообразная
, следовательно, интегрируема на [a, b]. Ее первообразная
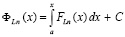 (25)
(25)
при 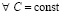 определена и непрерывна
определена и непрерывна 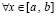 .
.
Первообразную (25) можно построить из полиномов (15).
В случае 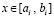 интеграл
интеграл
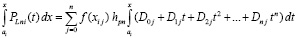 . (26)
. (26)
представляет собой первообразную полинома (15). Равенство (26) эквивалентно равенству
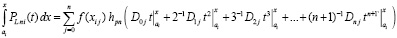 . (27)
. (27)
Для полинома (27) вводится обозначение при 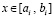
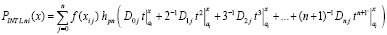 , (28)
, (28)
так что
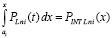 . (29)
. (29)
В (28) каждая нижняя подстановка равна нулю, поэтому
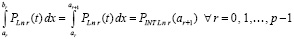 . (30)
. (30)
Из (29), (30) следует
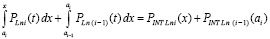 . (31)
. (31)
С учетом (23)
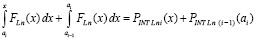 ,
,
или, с учетом (13),
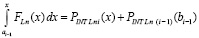 . (32)
. (32)
Аналогично, добавление к обеим частям (31) интеграла 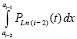 влечет
влечет
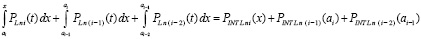 .
.
С учетом определения (23) функции 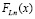 ,
,
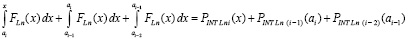 ,
,
или, аналогично (32),
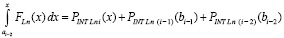 .
.
Процесс можно продолжать до получения индекса i – i = 0 в нижнем пределе интегрирования. Поскольку a0 = a, в продолжение процесса получится при 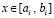
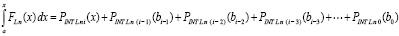 . (33)
. (33)
Из изложенного вытекает
Лемма 1. Первообразная (22) может вычисляться с помощью непрерывного кусочно-интерполяционного приближения (23) подынтегральной функции из соотношения
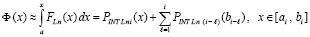 , (34)
, (34)
где 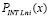 из (28),
из (28), 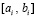 – из (13),
– из (13), 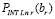 вычисляется из (28) при i = r, x = br.
вычисляется из (28) при i = r, x = br.
Первообразная (25), (33) представляет собой непрерывное аналитическое приближение первообразной подынтегральной функции (22), если первообразная от последней аналитического выражения не имеет. Из (33), (34) при x = b получается формула приближенного вычисления интеграла
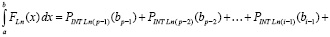
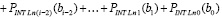 . (35)
. (35)
Более точно, имеет место
Теорема 2. В условиях леммы 1
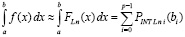 , (36)
, (36)
где 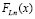 определяется из (23),
определяется из (23), 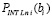 вычисляется из (28) при x = bi .
вычисляется из (28) при x = bi .
В обозначении (25) первообразная (33) примет вид
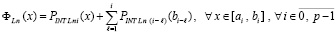 . (37)
. (37)
Для (37) по основной теореме интегрального исчисления [9] должно выполняться равенство
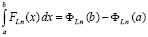 . (38)
. (38)
Более подробно,
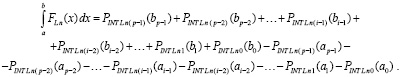 (39)
(39)
Из (28) 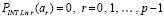 , и из (38), (39)
, и из (38), (39)
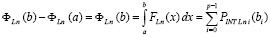 .
.
Окончательно,
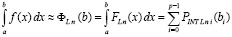 ,
,
что является разновидностью записи (36).
Для коэффициентов полинома 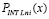 из (28) вводится обозначение
из (28) вводится обозначение
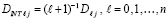 . (40)
. (40)
Полином (28) примет вид
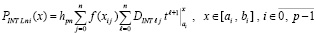 . (41)
. (41)
В качестве примера в табл. 3 даны коэффициенты (40) полинома (41), поделенные на n, для степени n = 4.
Таблица 3
Значения коэффициентов 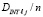 для приближения первообразной в случае полинома Лагранжа степени n = 4
для приближения первообразной в случае полинома Лагранжа степени n = 4
|
i |
|
|
0 |
(1, -1.041666666666666666667E+0, 4.861111111111111111111E-1, -1.041666666666666666667E-1, 8.333333333333333333333E-3) |
|
1 |
(0, 2.000000000000000000000E+0, -1.444444444444444444444E+0, 3.750000000000000000000E-1, -3.333333333333333333333E-2) |
|
2 |
(0, -1.500000000000000000000E+0, 1.583333333333333333333E+0, -5.000000000000000000000E-1, 5.000000000000000000000E-2) |
|
3 |
(0, 6.666666666666666666667E-1, -7.777777777777777777778E-1, 2.916666666666666666667E-1, -3.333333333333333333333E-2) |
|
4 |
(0, -1.250000000000000000000E-1, 1.527777777777777777778E-1, -6.250000000000000000000E-2, 8.333333333333333333333E-3) |
При вычислении (41) используется схема (8) для внутренней суммы, затем находится внешняя сумма парных произведений. Вычисление (37) сводится к сложению значения (41) с суммой значений аналогичных полиномов на правых границах предшествующих подынтервалов. В последовательном варианте можно переходить от подынтервала к подынтервалу, добавляя к текущему значению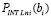 суммы по одному слагаемому
суммы по одному слагаемому 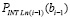 с границы предшествующего подынтервала. При x = b определяется приближение интеграла.
с границы предшествующего подынтервала. При x = b определяется приближение интеграла.
Замечание 3. Для рассматриваемого варианта метода можно повторить замечание 2: на последнем подынтервале следует заново рассчитать шаг интерполяции 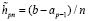 , взяв точные границы подынтервала.
, взяв точные границы подынтервала.
Программа вычисления интеграла на основе первообразной от кусочно-интерполяцинного приближения подынтегральной функции с помощью полинома Лагранжа и коэффициентов табл. 3 представлена непосредственно ниже.
program PIL_integral_n4_perv; {$APPTYPE CONSOLE} uses SysUtils; var a,b,S:extended; p:int64;
function f(x:extended):extended;
begin f:=cos(x)*exp(sin(x)){cos(x)}{sqrt(1-0.5*sqr(sin(x)))}{exp(x/2)+cos(4*x)}{x*exp(-x)*cos(2*x)} end;
function exact_int(a,b:extended):extended;
begin exact_int:=exp(sin(b))-exp(sin(a)){sin(b)-sin(a)}{1.35064388104767550252}{2*(exp(Pi)-1)}
{1/25*(exp(-2*Pi)*(3-10*Pi)-3)} end;
function PIL_int(a,b:extended; p:int64):extended;
const n=4; Dint:array[0..n,0..n] of extended =
((1, -1.041666666666666666667, 4.861111111111111111111E-1, -1.041666666666666666667E-1,
8.333333333333333333333E-3), (0, 2, -1.444444444444444444444E+0, 3.75E-1,
-3.333333333333333333333E-2),
(0, -1.5, 1.583333333333333333333, -5.0E-1, 5.0E-2), (0, 6.666666666666666666667E-1,
-7.777777777777777777778E-1, 2.916666666666666666667E-1, -3.333333333333333333333E-2),
(0, -1.25E-1, 1.527777777777777777778E-1, -6.25E-2, 8.333333333333333333333E-3));
var ai,hp,hpn,s,pp2:extended; j,r:byte;i:int64; c:array[0..n] of extended;
begin for j:=0 to n do begin pp2:= Dint[j][n]; for r:=1 to n do pp2 := pp2*n + Dint[j][n-r]; c[j]:=pp2; end;
hp:=(b-a)/p; hpn:=hp/n; i:=0; ai:=a; s:=0;
repeat for j:=0 to n do s:=s+c[j]*(f(ai+j*hpn)); inc(i); ai:=a+i*hp; until i = p;
PIL_int:=s*hp; end;
begin
a:=0; b:=Pi/2; p:=1024; S:=PIL_int(a, b, p); writeln(‘S=’, S, ‘ Pogr=’, abs(S-exact_int(a,b))); readln;
end.
Реализация дана для n = 4, повышение степени интерполяционного полинома к улучшению точности не приводит. Результаты численных экспериментов с программой PIL_integral_n4_perv приведены в табл. 4.
Таблица 4
Результаты приближенного вычисления интегралов с помощью программы PIL_integral_n4_perv
|
Интеграл |
Приближение интеграла |
Абсолютная погрешность приближения |
Параметры программы |
|
|
1.71828182845905E+0000 |
4.33680868994202E-0019 |
n = 4, p = 1024 |
|
|
-3.73603552314934E-0001 |
1.89735380184963E-0019 |
n = 4, p = 1024000 |
|
|
1.00000000000000E+0000 |
1.08420217248550E-0019 |
n = 4, p = 2048 |
|
|
1.35064388104768E+0000 |
0.00000000000000E+0000 |
n = 4, p = 64 |
|
|
4.42813852655585E+0001 |
1.38777878078145E-0017 |
n = 4, p = 4096 |
|
|
-1.22122604618968E-0001 |
2.50721752387273E-0019 |
n = 4, p = 2048 |
Сумму (35), аналогично (34), можно вычислять параллельно с использованием схемы сдваивания. С оговоркой относительно распараллеливания вычисления двойной суммы (35), с точностью до числового множителя сохранится оценка (21).
Замечание 4. Возможность представления (33) как непрерывного аналитического приближения первообразной подынтегральной функции является отличительной особенностью метода, обусловленной алгебраической формой полиномов с числовыми коэффициентами, приближающих подынтегральную функцию и интеграл. Известные методы аналогичную возможность непосредственно не предоставляют.
Целесообразно исследовать применимость непрерывного аналитического приближения первообразной для приближенного решения интегральных уравнений на основе кусочной интерполяции [10; 11], а также для приближенного решения дифференциальных уравнений на этой же основе [12]. Согласно эксперименту погрешность приближенного вычисления первообразной изложенным способом имеет такой же порядок, как погрешность вычисления интеграла (табл. 4).
Аналитические оценки погрешности кусочно-интерполяционного вычисления интеграла. Очевидно,
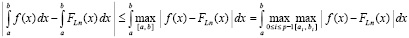 .
.
Отсюда
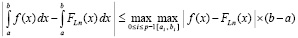 . (42)
. (42)
Согласно (23)
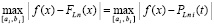 . (43)
. (43)
Погрешность интерполяции функции f(x) полиномом Лагранжа на подынтервале оценивается следующим образом [1; 12]. При 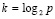 справедливо неравенство
справедливо неравенство
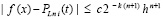 ,
, 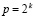 ,
, 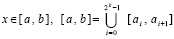 . (44)
. (44)
Лемма 2 [12]. Пусть для произвольного n = const функция f(x) определена, непрерывна и непрерывно дифференцируема n + 1 раз на отрезке [a, b] из (13), на концах которого подразумеваются соответственные односторонние производные. Тогда, каково бы ни было n ≥ 1, последовательность полиномов 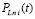 из (15) равномерно сходится к функции f(x) на данном отрезке при k → ∞, где
из (15) равномерно сходится к функции f(x) на данном отрезке при k → ∞, где 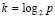 , p – число подынтервалов из (13). Скорость сходимости оценивается из (44), где c = const,
, p – число подынтервалов из (13). Скорость сходимости оценивается из (44), где c = const, 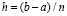 – шаг интерполяции полинома
– шаг интерполяции полинома 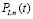 из (9) на [a, b] при k = 0.
из (9) на [a, b] при k = 0.
При 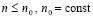 , имеет место
, имеет место
Следствие 1 [12]. В условиях леммы 2, а также в предположении h < 1, выполняется неравенство
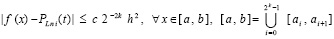 , (45)
, (45)
где c = const не зависит от выбора степени полинома n.
Подстановка (44) в (43) и соответственно в (42) влечет
Следствие 2. В условиях леммы 2 имеет место сходимость рассматриваемого приближения 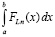 к интегралу
к интегралу 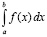 при k → ∞, для скорости сходимости верна оценка
при k → ∞, для скорости сходимости верна оценка
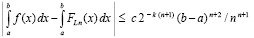 . (46)
. (46)
Аналогичная подстановка (45) влечет
Следствие 3. В условиях следствия 1 также имеет место сходимость рассматриваемого приближения интеграла, для скорости сходимости верна оценка
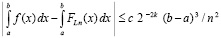 . (47)
. (47)
Следствия 2, 3 и оценки (46), (47) дополняют утверждения лемм 1, 2 и теоремы 2.
Рассмотренные условия и оценки уточняют аналоги, ранее приведенные в [1]. В частности, при n = 2 оценка (47) перейдет в оценку
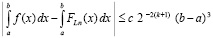 ,
,
которая верна при условии трехкратной дифференцируемости подынтегральной функции.
Кусочно-интерполяционное вычисление интеграла на основе полиномов Ньютона. При каждом i из (13) интерполяционный полином Ньютон а для интерполирования вперед с равноотстоящими узлами на i-м подынтервале имеет вид [5]
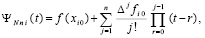
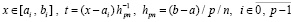 , (48)
, (48)
где узлы интерполяции 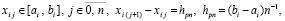
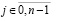 ,
, 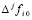 – конечная разность j-го порядка в узле
– конечная разность j-го порядка в узле 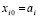 , p из (13). Поскольку интерполяционные полиномы равной степени с одинаковыми узлами и узловыми значениями совпадают, то для последовательности полиномов
, p из (13). Поскольку интерполяционные полиномы равной степени с одинаковыми узлами и узловыми значениями совпадают, то для последовательности полиномов 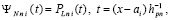 верны оценка (44), лемма 2, следствие 1 и оценка (45), а последовательность полиномов (48) в условиях леммы 2 и следствия 1 сходится к f(x) на [a, b], если p → ∞.
верны оценка (44), лемма 2, следствие 1 и оценка (45), а последовательность полиномов (48) в условиях леммы 2 и следствия 1 сходится к f(x) на [a, b], если p → ∞.
На каждом подынтервале 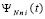 можно преобразовать к виду алгебраического полинома с числовыми коэффициентами. Для этого каждый полином
можно преобразовать к виду алгебраического полинома с числовыми коэффициентами. Для этого каждый полином 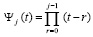 из (48) преобразуется в полином с целочисленными коэффициентами. Если положить
из (48) преобразуется в полином с целочисленными коэффициентами. Если положить 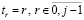 , по схеме (2) получится
, по схеме (2) получится
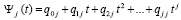 , (49)
, (49)
где коэффициенты – целые числа. Почленное деление таких полиномов на j! в (48) повлечет развернутую форму полинома вида
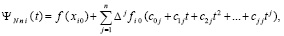
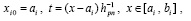
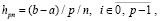 (50)
(50)
где
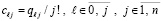 , (51)
, (51)
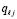 из (49). С учетом
из (49). С учетом 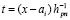 отсюда следует
отсюда следует
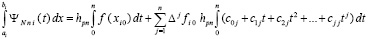 .
.
Подстановка пределов интегрирования влечет
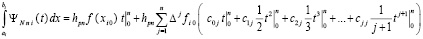 ,
,
или
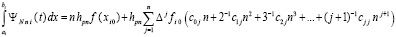 . (52)
. (52)
Сложение (52) по всем подынтервалам влечет формулу приближения интеграла. С учетом равенства интерполяционных полиномов Лагранжа и Ньютона в случае совпадения узлов и значений в узлах интерполяции имеет место
Теорема 3. На основе кусочной интерполяции подынтегральной функции с помощью полиномов Ньютона (48) значение интеграла можно приближенно вычислить из соотношения
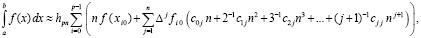
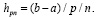 (53)
(53)
где 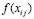 – значение подынтегральной функции в j-м узле интерполяции на i-м подынтервале из (13),
– значение подынтегральной функции в j-м узле интерполяции на i-м подынтервале из (13), 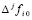 – конечная разность j-го порядка в узле
– конечная разность j-го порядка в узле 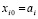 , p из (13), коэффициенты и числовые параметры определяются согласно (49), (50), (51). Погрешность приближения в условиях леммы 2 и следствий 1 – 3 оценивается, соответственно, из (46), (47) при соответственной замене обозначений.
, p из (13), коэффициенты и числовые параметры определяются согласно (49), (50), (51). Погрешность приближения в условиях леммы 2 и следствий 1 – 3 оценивается, соответственно, из (46), (47) при соответственной замене обозначений.
Выражение в скобках внутренней суммы в (53) является числом, зависящим от степени интерполяционного полинома и от номера узла интерполяции, но не зависящим от номера подынтервала и вида подынтегральной функции. Ниже это число обозначается
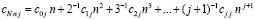 . (54)
. (54)
Тогда (53) можно записать в виде
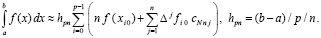 (55)
(55)
Формулы (53), (55) могут непросредственно использоваться для вычисления интеграла. Коэффициенты cNnj априори вычисляются для всех функций и подынтервалов, записываются в память компьютера (в раздел описания констант программы) и в таком виде применяются для вычисления интегралов. Непосредственно ниже приводится таблица значений cNnj из (54), (55) для различных степеней полинома Ньютона.
Таблица 5
Значения коэффициентов cNnj / n вычисления интеграла из (55) для различных степеней n интерполяционного полинома Ньютона
|
n |
cNnj / n, |
|
1 |
(5.000000000000000000000E-1) |
|
2 |
(1.000000000000000000000E+0, 1.666666666666666666667E-1) |
|
3 |
(1.500000000000000000000E+0, 7.500000000000000000000E-1, 1.250000000000000000000E-1) |
|
4 |
(2.000000000000000000000E+0, 1.666666666666666666667E+0, 6.666666666666666666667E-1, 7.777777777777777777778E-2) |
|
5 |
(2.500000000000000000000E+0, 2.916666666666666666667E+0, 1.875000000000000000000E+0, 5.902777777777777777778E-1, 6.597222222222222222222E-2) |
|
6 |
(3.000000000000000000000E+0, 4.500000000000000000000E+0, 4.000000000000000000000E+0, 2.050000000000000000000E+0, 5.500000000000000000000E-1, 4.880952380952380952381E-2) |
|
7 |
(3.500000000000000000000E+0, 6.416666666666666666667E+0, 7.291666666666666666667E+0, 5.181944444444444444444E+0, 2.231250000000000000000E+0, 5.112268518518518518519E-1, 4.346064814814814814815E-2) |
|
8 |
(4.000000000000000000000E+0, 8.666666666666666666667E+0, 1.200000000000000000000E+1, 1.091111111111111111111E+1, 6.488888888888888888889E+0, 2.397883597883597883598E+0, 4.867724867724867724868E-1, 3.488536155202821869489E-2) |
|
9 |
(4.500000000000000000000E+0, 1.125000000000000000000E+1, 1.837500000000000000000E+1, 2.036250000000000000000E+1, 1.546875000000000000000E+1, 7.897767857142857142857E+0, 2.565401785714285714286E+0, 4.626562500000000000000E-1, 3.188616071428571428571E-2) |
|
10 |
(5.000000000000000000000E+0, 1.416666666666666666667E+1, 2.666666666666666666667E+1, 3.486111111111111111111E+1, 3.225000000000000000000E+1, 2.102843915343915343915E+1, 9.417989417989417989418E+0, 2.724316578483245149912E+0, 4.458774250440917107584E-1, 2.683414836192613970392E-2) |
Программная реализация кусочно-интерполяционного вычисления интеграла на основе полинома Ньютона и соотношения (55) имеет следующий вид.
program PIN_integral_n1_10; {$APPTYPE CONSOLE} uses SysUtils; var a,b,S:extended; n:byte; p:int64;
function f(x:extended):extended;
begin f:=cos(x)*exp(sin(x)){cos(x)}{sqrt(1-0.5*sqr(sin(x)))}{exp(x/2)+cos(4*x)}{x*exp(-x)*cos(2*x)} end;
function exact_int(a,b:extended):extended;
begin exact_int:=exp(sin(b))-exp(sin(a)){sin(b)-sin(a)}{1.35064388104767550252}{2*(exp(Pi)-1)}
{1/25*(exp(-2*Pi)*(3-10*Pi)-3)} end;
function PIN_int(a,b:extended; n:byte; p:int64):extended; type coeff = array[0..10] of extended;
const c:array[1..10,1..10] of extended =
((0.5, 0, 0, 0, 0, 0, 0, 0, 0, 0), (1,1.666666666666666666667E-1, 0, 0, 0, 0, 0, 0, 0, 0),
(1.5, 7.5E-1, 1.25E-1, 0, 0, 0, 0, 0, 0, 0), (2, 1.666666666666666666667E+0, 6.666666666666666666667E-1,
7.777777777777777777778E-2, 0, 0, 0, 0, 0, 0), (2.5, 2.916666666666666666667E+0, 1.875,
5.902777777777777777778E-1, 6.597222222222222222222E-2, 0, 0, 0, 0, 0), (3, 4.5, 4, 2.05, 5.5E-1,
4.880952380952380952381E-2, 0, 0, 0, 0), (3.5, 6.416666666666666666667E+0,
7.291666666666666666667E+0, 5.181944444444444444444E+0, 2.23125E+0,
5.112268518518518518519E-1, 4.346064814814814814815E-2, 0, 0, 0),
(4, 8.666666666666666666667E+0, 1.2E+1, 1.091111111111111111111E+1,
6.488888888888888888889E+0, 2.397883597883597883598E+0, 4.867724867724867724868E-1,
3.488536155202821869489E-2, 0, 0), (4.5, 1.125E+1, 1.8375E+1, 2.03625E+1, 1.546875E+1,
7.897767857142857142857E+0, 2.565401785714285714286E+0, 4.6265625E-1,
3.188616071428571428571E-2,0), (5, 1.416666666666666666667E+1, 2.666666666666666666667E+1,
3.486111111111111111111E+1, 3.225E+1, 2.102843915343915343915E+1, 9.417989417989417989418E+0,
2.724316578483245149912E+0, 4.458774250440917107584E-1, 2.683414836192613970392E-2));
var ai,hp,hpn:extended; j:byte; i:int64; dy0:coeff;
procedure Konech_Raznoct(n:byte;a00,h:extended; var dy0:coeff);
var r,k:byte; x:coeff; dy:array[0..10, 0..10] of extended;
begin for r:=0 to n do x[r]:=a00+r*h; for r:=0 to n-1 do dy[1,r]:=f(x[r+1])-f(x[r]);
for k:=2 to n do for r:=0 to n-k do dy[k,r]:=dy[k-1,r+1]-dy[k-1,r]; for k:=1 to n do dy0[k]:=dy[k,0]; end;
begin hp:=(b-a)/p; hpn:=hp/n; ai:=a; i:=0;s:=0;
repeat
Konech_Raznoct(n,ai,hpn,dy0); s:=s + f(ai); for j:=1 to n do s:= s + dy0[j]*c[n,j]; inc(i); ai:=a+i*hp;
until i = p; PIN_int:=s*hp;
end;
begin
a:=0; b:=Pi/2; n:=6; p:=64; S:=PIN_int(a,b,n,p); writeln(‘S=’,S,’ Pogr=’,abs(S-exact_int(a,b))); readln;
end.
Результаты численных экспериментов с программой PIN_integral_n1_10 приведены в табл. 6.
Таблица 6
Результаты численного эксперимента по приближению интеграла из соотношения (55)
|
Интеграл |
Приближение интеграла |
Абсолютная погрешность приближения |
Параметры программы |
|
|
1.71828182845905E+0000 |
0.00000000000000E+0000 |
n = 6, p = 64 |
|
|
-3.73603552314934E-0001 |
4.60785923306339E-0019 |
n = 8, p = 4096 |
|
|
1.00000000000000E+0000 |
0.00000000000000E+0000 |
n = 7, p = 32 |
|
|
1.35064388104768E+0000 |
0.00000000000000E+0000 |
n = 1, p = 16 |
|
|
4.42813852655585E+0001 |
0.00000000000000E+0000 |
n = 5, p = 512 |
|
|
-1.22122604618968E-0001 |
0.00000000000000E+0000 |
n = 10, p = 512 |
На основе интерполяционного полинома Ньютона можно также приблизить первообразную (22). Пусть рассматривается кусочно-интерполяционное приближение подынтегральной функции
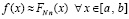 ,
,
где
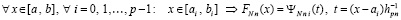 , (56)
, (56)
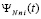 из (50). Пусть по-прежнему f(x) непрерывна
из (50). Пусть по-прежнему f(x) непрерывна 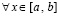 из (13). Тогда эта функция интегрируема, ее первообразная (22) непрерывна на [a, b]. Приближение подынтегральной функции
из (13). Тогда эта функция интегрируема, ее первообразная (22) непрерывна на [a, b]. Приближение подынтегральной функции 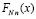 рассматривается как самостоятельная функция, определенная на всем [a, b], при этом определяющими являются соотношения (56). Как и в случае полинома Лагранжа, начальный и конечный узел интерполяции полинома (50) всегда находятся соответственно на левой и правой границе подынтервала, поэтому при
рассматривается как самостоятельная функция, определенная на всем [a, b], при этом определяющими являются соотношения (56). Как и в случае полинома Лагранжа, начальный и конечный узел интерполяции полинома (50) всегда находятся соответственно на левой и правой границе подынтервала, поэтому при 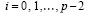
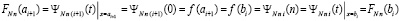 . (57)
. (57)
Согласно (56), (57) функция 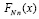 непрерывна
непрерывна 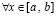 , поэтому интегрируема на [a, b]. Ее первообразная,
, поэтому интегрируема на [a, b]. Ее первообразная,
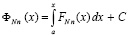 , (58)
, (58)
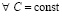 определена и непрерывна
определена и непрерывна 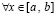 . Первообразную (58) можно построить из полиномов (50). В случае
. Первообразную (58) можно построить из полиномов (50). В случае 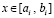 интеграл
интеграл
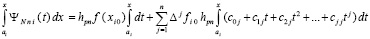 (59)
(59)
представляет собой первообразную полинома (50). Равенство (59) эквивалентно
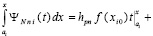
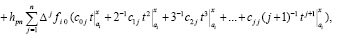
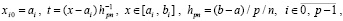 (60)
(60)
Для полинома (60) вводится обозначение
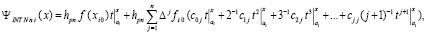
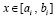 . (61)
. (61)
В этом обозначении
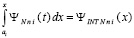 . (62)
. (62)
В скобках (60), (61) каждая нижняя подстановка равна нулю, поэтому
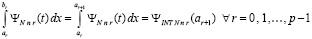 . (63)
. (63)
Из (62), (63) следует
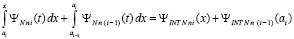 .
.
Отсюда с учетом (56)
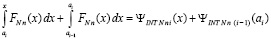 ,
,
или, с учетом (13),
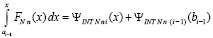 . (64)
. (64)
Аналогично, добавление к обеим частям (64) 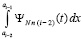 влечет
влечет
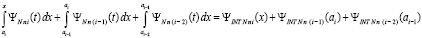 .
.
С учетом определения (56) функции 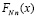
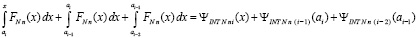 ,
,
или,
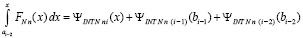 .
.
Процесс можно продолжать до получения нулевого индекса в нижнем пределе интегрирования. С учетом a0 = a получится
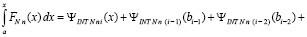
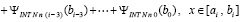 . (65)
. (65)
В краткой записи
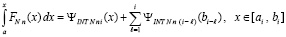 . (66)
. (66)
Таким образом, первообразная (58) кусочно-интерполяционного приближения (56) подынтегральной функции выражается из (65), (66). При этом 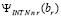 вычисляется из (61). Первообразная (58) аналитически и непрерывно приближает первообразную подынтегральной функции, если первообразная последней сама по себе аналитического выражения не имеет. При x = b эти соотношения дают формулу приближенного вычисления интеграла
вычисляется из (61). Первообразная (58) аналитически и непрерывно приближает первообразную подынтегральной функции, если первообразная последней сама по себе аналитического выражения не имеет. При x = b эти соотношения дают формулу приближенного вычисления интеграла
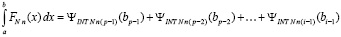
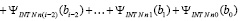 ,
,
точнее,
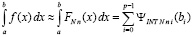 , (67)
, (67)
где 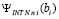 вычисляется из (61) при x = bi.
вычисляется из (61) при x = bi.
В обозначении (62) первообразная (58) представляется в виде
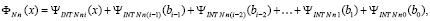
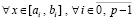 , (68)
, (68)
Лемма 3. На основе кусочной интерполяции подынтегральной функции с помощью полиномов Ньютона (48) первообразная (22) приближенно вычисляется из соотношения
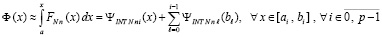 , (69)
, (69)
где 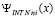 определяется из (61),
определяется из (61), 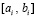 – из (13).
– из (13).
По основной теореме интегрального исчисления для (68), (69) должно выполняться равенство
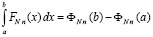 .
.
Аналогично (39),
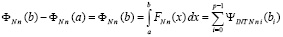 ,
,
что также приводит к (67). Окончательно, имеет место
Теорема 4. В условиях леммы 3
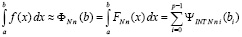 , (70)
, (70)
где 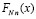 определяется из (57),
определяется из (57), 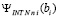 вычисляется из (61) при x = bi . На случай кусочной интерполяции подынтегральной функции с помощью полиномов Ньютона (48) дословно переносятся лемма 2, следствия 1 – 3 при условии замены в этих утверждениях
вычисляется из (61) при x = bi . На случай кусочной интерполяции подынтегральной функции с помощью полиномов Ньютона (48) дословно переносятся лемма 2, следствия 1 – 3 при условии замены в этих утверждениях 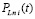 из (15) на
из (15) на 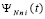 из (50), (51) и
из (50), (51) и 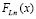 из (23) на
из (23) на 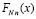 из (56). При n = 2 оценка (47) перейдет в оценку
из (56). При n = 2 оценка (47) перейдет в оценку
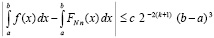 ,
,
которая верна при условии трехкратной дифференцируемости подынтегральной функции.
Коэффициенты полинома 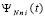 из (50),
из (50), 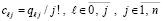 , где
, где 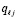 из (49), не зависят от подынтегральной функции, от номера подынтервала, от диапазона независимой переменной, они зависят от степени полинома, номера коэффициента и от номера узла интерполяции. Эти коэффициенты можно вычислить априори для всех функций и подынтервалов, записать в память компьютера (в раздел описания констант программы) и хранить для вычисления интегралов рассматриваемого вида. В качестве примера ниже приводится таблица значений коэффициентов
из (49), не зависят от подынтегральной функции, от номера подынтервала, от диапазона независимой переменной, они зависят от степени полинома, номера коэффициента и от номера узла интерполяции. Эти коэффициенты можно вычислить априори для всех функций и подынтервалов, записать в память компьютера (в раздел описания констант программы) и хранить для вычисления интегралов рассматриваемого вида. В качестве примера ниже приводится таблица значений коэффициентов 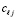 для интерполяционного полинома Ньютона степени n = 10.
для интерполяционного полинома Ньютона степени n = 10.
Таблица 7
Значения коэффициентов 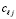 для полинома Ньютона степени n = 10
для полинома Ньютона степени n = 10
|
j |
|
|
1 |
(0, 5.000000000000000000000E-1) |
|
2 |
(0, -2.500000000000000000000E-1, 1.666666666666666666667E-1) |
|
3 |
(0, 1.666666666666666666667E-1, -1.666666666666666666667E-1, 4.166666666666666666667E-2) |
|
4 |
(0, -1.250000000000000000000E-1, 1.527777777777777777778E-1, -6.250000000000000000000E-2, 8.333333333333333333333E-3) |
|
5 |
(0, 1.000000000000000000000E-1, -1.388888888888888888889E-1, 7.291666666666666666667E-2, -1.666666666666666666667E-2, 1.388888888888888888889E-3) |
|
6 |
(0, -8.333333333333333333333E-2, 1.268518518518518518519E-1, -7.812500000000000000000E-2, 2.361111111111111111111E-2, -3.472222222222222222222E-3, 1.984126984126984126984E-4) |
|
7 |
(0, 7.142857142857142857143E-2, -1.166666666666666666667E-1, 8.055555555555555555556E-2, -2.916666666666666666667E-2, 5.787037037037037037037E-3, -5.952380952380952380952E-4, 2.480158730158730158730E-5) |
|
8 |
(0, -6.250000000000000000000E-2, 1.080357142857142857143E-1, -8.142361111111111111111E-2, 3.357638888888888888889E-2, -8.101851851851851851852E-3, 1.140873015873015873016E-3, -8.680555555555555555556E-5, 2.755731922398589065256E-6) |
|
9 |
(0, 5.555555555555555555556E-2, -1.006613756613756613757E-1, 8.137951940035273368607E-2, -3.708333333333333333333E-2, 1.031057098765432098765E-2, -1.785714285714285714286E-3, 1.880787037037037037037E-4, -1.102292768959435626102E-5, 2.755731922398589065256E-7) |
|
10 |
(0, -5.000000000000000000000E-2, 9.429894179894179894180E-2, -8.079117063492063492063E-2, 3.988536155202821869489E-2, -1.236979166666666666667E-2, 2.490906084656084656085E-3, -3.255208333333333333333E-4, 2.663874191651969429747E-5, -1.240079365079365079365E-6, 2.505210838544171877505E-8) |
При вычислении полинома (50) может использоваться схема (8) для внутренней суммы, затем вычисляется внешняя сумма парных произведений. Вычисление первообразной (65), (66) для 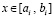 сводится к сложению значений полинома (50) с суммой значений аналогичных полиномов на правых границах предшествующих подынтервалов. В последовательном варианте вычислений можно переходить от подынтервала к подынтервалу, добавляя к текущему значению
сводится к сложению значений полинома (50) с суммой значений аналогичных полиномов на правых границах предшествующих подынтервалов. В последовательном варианте вычислений можно переходить от подынтервала к подынтервалу, добавляя к текущему значению 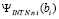 по одному слагаемому
по одному слагаемому 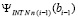 с границы предшествующего подынтервала. При x = b получится значение определенного интеграла.
с границы предшествующего подынтервала. При x = b получится значение определенного интеграла.
Замечание 5. Для рассматриваемого варианта можно повторить замечание 2: на последнем подынтервале надо заново рассчитать шаг интерполяции 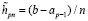 , взяв точные границы подынтервала.
, взяв точные границы подынтервала.
Программная реализация вычисления интеграла на основе полинома Ньютона с коэффициентами из табл. 7 имеет следующий вид.
program PIN_integral_n10_perv; {$APPTYPE CONSOLE} uses SysUtils; var a,b,S:extended; p:int64;
function f(x:extended):extended;
begin f:=cos(x)*exp(sin(x)){cos(x)}{sqrt(1-0.5*sqr(sin(x)))}{exp(x/2)+cos(4*x)}{x*exp(-x)*cos(2*x)} end;
function exact_int(a,b:extended):extended;
begin exact_int:=exp(sin(b))-exp(sin(a)){sin(b)-sin(a)}{1.35064388104767550252}{2*(exp(Pi)-1)}
{1/25*(exp(-2*Pi)*(3-10*Pi)-3)} end;
function PIN_int(a,b:extended; p:int64):extended; const n=10;
Cint:array[1..n,0..n] of extended =((0, 5.000000000000000000000E-1, 0, 0, 0, 0, 0, 0, 0, 0, 0),
(0, -2.500000000000000000000E-1, 1.666666666666666666667E-1, 0, 0, 0, 0, 0, 0, 0, 0),
(0, 1.666666666666666666667E-1, -1.666666666666666666667E-1, 4.166666666666666666667E-2, 0, 0, 0,
0, 0, 0, 0), (0, -1.250000000000000000000E-1, 1.527777777777777777778E-1,
-6.250000000000000000000E-2, 8.333333333333333333333E-3, 0, 0, 0, 0, 0, 0),
(0, 1.000000000000000000000E-1, -1.388888888888888888889E-1, 7.291666666666666666667E-2,
-1.666666666666666666667E-2, 1.388888888888888888889E-3, 0, 0, 0, 0, 0),
(0, -8.333333333333333333333E-2, 1.268518518518518518519E-1, -7.812500000000000000000E-2,
2.361111111111111111111E-2, -3.472222222222222222222E-3, 1.984126984126984126984E-4, 0, 0, 0, 0),
(0, 7.142857142857142857143E-2, -1.166666666666666666667E-1, 8.055555555555555555556E-2,
-2.916666666666666666667E-2, 5.787037037037037037037E-3, -5.952380952380952380952E-4,
2.480158730158730158730E-5, 0, 0, 0), (0, -6.250000000000000000000E-2, 1.080357142857142857143E-1,
-8.142361111111111111111E-2, 3.357638888888888888889E-2, -8.101851851851851851852E-3,
1.140873015873015873016E-3, -8.680555555555555555556E-5, 2.755731922398589065256E-6, 0, 0),
(0, 5.555555555555555555556E-2, -1.006613756613756613757E-1, 8.137951940035273368607E-2,
-3.708333333333333333333E-2, 1.031057098765432098765E-2, -1.785714285714285714286E-3,
1.880787037037037037037E-4, -1.102292768959435626102E-5, 2.755731922398589065256E-7, 0),
(0, -5.000000000000000000000E-2, 9.429894179894179894180E-2, -8.079117063492063492063E-2,
3.988536155202821869489E-2, -1.236979166666666666667E-2, 2.490906084656084656085E-3,
-3.255208333333333333333E-4, 2.663874191651969429747E-5, -1.240079365079365079365E-6,
2.505210838544171877505E-8));
type coeff = array[0..10] of extended; var ai,hp,hpn,s,pp2:extended; j,r:byte;i:int64; c:array[0..n] of extended;
dy0:coeff;
procedure Konech_Raznoct(n:byte;a00,h:extended; var dy0:coeff);
var r,k:byte; x:coeff; dy:array[0..10,0..10] of extended;
begin for r:=0 to n do x[r]:=a00+r*h; for r:=0 to n-1 do dy[1,r]:=f(x[r+1])-f(x[r]);
for k:=2 to n do for r:=0 to n-k do dy[k,r]:=dy[k-1,r+1]-dy[k-1,r]; for k:=1 to n do dy0[k]:=dy[k,0]; end;
begin
for j:=1 to n do begin pp2:= Cint[j][n]; for r:=1 to n do pp2 := pp2*n + Cint[j][n-r]; c[j]:=pp2; end;
hp:=(b-a)/p; hpn:=hp/n; i:=0; ai:=a; s:=0;
repeat
Konech_Raznoct(n,ai,hpn,dy0); s:= s + f(ai); for j:=1 to n do s:= s + dy0[j]*c[j]; inc(i); ai:=a+i*hp;
until i = p; PIN_int:=s*hp;
end;
begin
a:=0; b:=Pi/2; p:=8; S:=PIN_int(a, b, p); writeln(‘S=’, S, ‘ Pogr=’, abs(S-exact_int(a,b))); readln;
end.
Результаты работы программы представлены непосредственно ниже.
Таблица 8
Результаты численного эксперимента по приближению интеграла с помощью программы PIN_integral_n10_perv
|
Интеграл |
Приближение интеграла |
Абсолютная погрешность приближения |
Параметры программы |
|
|
1.71828182845905E+0000 |
2.16840434497101E-0019 |
n = 10, p = 8 |
|
|
-3.73603552314934E-0001 |
7.31836466427715E-0019 |
n = 10, p = 2000 |
|
|
1.00000000000000E+0000 |
0.00000000000000E+0000 |
n = 10, p = 16 |
|
|
1.35064388104768E+0000 |
1.08420217248550E-0019 |
n = 10, p = 16 |
|
|
4.42813852655585E+0001 |
0.00000000000000E+0000 |
n = 10, p = 8 |
|
|
-1.22122604618968E-0001 |
0.00000000000000E+0000 |
n = 10, p = 512 |
Согласно эксперименту погрешность приближения первообразной изложенным способом имеет такой же порядок, как погрешность вычисления интеграла в табл. 8.
Обсуждение вариантов приближения интегралов, первообразных и стандартизации программ. Как видно из таблиц 2 и 6, приближение интеграла на основе полинома Лагранжа из соотношения (19) оказывается несколько точнее приближения на основе полинома Ньютона из (55). При этом оба приближения сравнительно точны и согласно эксперименту отличаются стабильностью. Кроме того, оба эти приближения превосходят по точности аналоги из [1], особенно положительно в данном отношении отличается приближение на основе полинома Лагранжа из (19). Данное приближение, кроме того, положительно отличается по трудоемкости, в частности, от методов вычисления интеграла, представленных в [6]. Напротив, сопоставление таблиц 4 и 8 показывает, что приближение на основе полинома Ньютона из соотношения (70) точнее приближения на основе полинома Лагранжа из (36). То же относится к приближениям первообразных, которые в обоих случаях являются аналитическими и непрерывными, что характерно отличает метод от известных [2; 6; 13]. По структуре отличие предложенного метода сохраняется относительно современных модификаций формул Ньютона-Котеса [14; 15]. Кроме того, согласно таблицам 2, 6 и на основании данных численных экспериментов, описанных в [2; 6], предложенный метод по отношению к существующим обладает потенциалом повышенной точности приближения. Однако для корректности такого сравнения нужна статистическая обработка данных, которая в изложенной выше работе не выполнялась. Необходимо отметить, что приближения полиномиального вида из соотношений (36) и (70) уступают в точности приближениям на основе линейных комбинаций из (19) и (55). Это объясняется тем, что вычисление полинома по схеме Горнера накапливает погрешность с ростом степени полинома больше, чем вычисление линейной комбинации с постоянными коэффициентами. По этой причине в табл. 4 пришлось ограничить эксперимент полиномом степени n = 4, а в табл. 8 – полиномом степени n = 10. Все рассмотренные варианты приближений интеграла являются сравнительно быстродействующими и обладают максимальным параллелизмом.
Программы, реализующие приближения, достаточно компактны, коэффициенты приближений в них являются хранимыми в разделах описания констант, отсюда сравнительное быстродействие их выполнения. Для запуска соответствующей программы пользователю достаточно задать на ее входе вид подынтегральной функции, промежуток интегрирования, степень полинома и число подынтервалов в качестве параметров. Можно упростить пользовательский интерфейс, если дополнить программу выбором наилучшего приближения подынтегральной функции. Автоматическая реализация такого приближения элементарно выполняется в [1]. В частности, оно осуществимо для наиболее высокой точности приближения путем соответствующего подбора степени n и числа подынтервалов p. В случае если программа таким образом модифицирована, пользователю достаточно задавать на входе только вид подынтегральной функции и границы промежутка интегрирования. Следует, однако, принять во внимание, что согласно практике компьютерных вычислений наилучшее приближение подынтегральной функции не означает наивысшую точность вычисления интеграла.
В заключение относительно точности приближения первообразной можно отметить следующее. Номер подынтервала, при котором 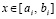 , есть
, есть 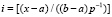 . В соотношении (69)
. В соотношении (69)  совпадает с интегралом
совпадает с интегралом 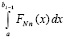 . Для повышения точности приближения первообразной этот интеграл можно вычислить из (55) с заменой b на
. Для повышения точности приближения первообразной этот интеграл можно вычислить из (55) с заменой b на 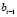 , и только на i-м подынтервале вычислить
, и только на i-м подынтервале вычислить 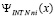 , затем сложить с полученным интегралом. Аналогично можно действовать при вычислении (33), (34).
, затем сложить с полученным интегралом. Аналогично можно действовать при вычислении (33), (34).
Заключение
Компьютерное вычисление интеграла от функции одной вещественной переменной выполняется на основе кусочно-интерполяционного приближения подынтегральной функции с помощью интерполяционных полиномов Лагранжа и Ньютона, преобразованных в каноническую форму алгебраических полиномов с числовыми коэффициентами. Коэффициенты интерполяционных полиномов записываются в память компьютера (в раздел описания констант программы), они инвариантны относительно вида подынтегральной функции и промежутка интегрирования. Фактически в работе выполнена разновидность реализации формул Ньютона-Котеса на основе кусочной интерполяции, при этом достигается сравнительно высокая точность приближения интеграла, в том числе на больших промежутках интегрирования, и стандартизируется пользовательский интерфейс программ, реализующих метод. Метод распространяется на непрерывное аналитическое компьютерное приближение первообразной подынтегральной функции. Выполнены численные эксперименты, показывающие стабильность метода для различных степеней полиномов, в частности достигается граница абсолютной погрешности вычисления интеграла на промежутке [a, b] = [0,500] порядка 10–20. При этом на практике достигается минимизация погрешности и временной сложности кусочно-интерполяционного вычисления интегралов, а также стандартизация программ, реализующих метод.
Библиографическая ссылка
Ромм Я.Е., Джанунц Г.А. О СТАНДАРТИЗАЦИИ ПРОГРАММ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ НА ОСНОВЕ КУСОЧНОЙ ИНТЕРПОЛЯЦИИ ПОДЫНТЕГРАЛЬНЫХ ФУНКЦИЙ // Современные наукоемкие технологии. 2023. № 4. С. 71-92;URL: https://top-technologies.ru/ru/article/view?id=39582 (дата обращения: 03.01.2026).
DOI: https://doi.org/10.17513/snt.39582




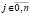
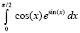
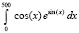
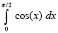
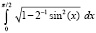
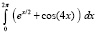
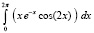
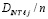 ,
, 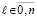
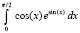
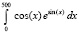
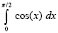
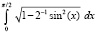
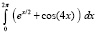
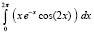
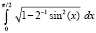
 ,
,