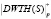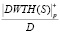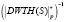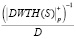Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Калмыков И.А. 1 Чистоусов Н.К. 1 Духовный Д.В. 1

---

1 ФГАОУ ВО «Северо-Кавказский федеральный университет»

Повышенный интерес к технологиям ортогонального частотного мультиплексирования (OFDM) обоснован тем, что их применение позволяет обеспечить высокую скорость передачи и спектральную эффективность, а также низкую межсимвольную интерференцию. Не являются исключением низкоорбитальные системы спутникового интернета (НССИ). Для повышения скорости передачи в беспроводных системах OFDM используются методы, которые увеличивают размерность QAM созвездия, уменьшают величину циклического префикса, увеличивают скорость кодирования, используют технологию МИМО. Однако вопросы сокращения времени цифровой обработки сигналов, которые реализуются с использованием быстрых преобразований Фурье (БПФ), не были широко рассмотрены. Повысить скорость обработки сигналов можно двумя способами. Во-первых, заменить БПФ на более скоростное ортогональное преобразование. В качестве такого преобразования можно взять вейвлет-преобразование (ВП) Хаара. Во-вторых, при обработке сигнала использовать табличную реализацию арифметических преобразований. Реализация целочисленных дискретных вейвлет-преобразований (ЦДВП) Хаара в конечных полях Галуа позволяет заменить операции сложения, вычитания и умножения на операцию выборки результата из LUT-таблицы. Очевидно, что интеграция данных способов позволит эффективно решить выявленную проблему – сокращение времени цифровой обработки сигналов в OFDM системе. Поэтому применение алгебраической системы конечного поля при реализации математической модели целочисленного вейвлет-преобразования Хаара является актуальной задачей.

Статья в формате PDF

362 KB

технология OFDM

вейвлет-преобразование Хаара

алгебраические системы

конечные поля Галуа

1. Michael Sheetz In race to provide internet from space, companies ask FCC for about 38,000 new broadband satellites. [Электронный ресурс]. URL: https://www.cnbc.com/2021/11/05/space-companies-ask-fcc-to-approve-38000-broadband-satellites.html (дата обращения: 02.04.2023).

2. McDowell J.C. The Low Earth Orbit Satellite Population and Impacts of the SpaceX Starlink Constellation// The Astrophysical Journal Letters. 2020. Vol. 892. P. 10–15. DOI: 10.3847/2041-8213/ab8016.

3. Пехтерев С.В., Макаренко С.И., Ковальский А.А. Описательная модель системы спутниковой связи Starlink // Системы управления, связи и безопасности (Systems of Control, Communication and Security). 2022. № 4. С. 190–255. URL: http://sccs.intelgr.com/archive/2022-04/07-Pehterev.pdf (дата обращения: 02.04.2023). DOI: 10.24412/2410-9916-2022-4-190-255.

4. Бакулин М.Г., Крейнделин В.Б., Шумов А.П. Технология OFDM. Учебное пособие для вузов. М.: Горячая линия – Телеком, 2017. 352 с.

5. Qasim Chaudhari A. Beginner’s Guide to OFDM. [Электронный ресурс]. URL: https://wirelesspi.com/a-beginners-guide-to-ofdm/ (дата обращения: 02.04.2023).

6. Hans-Georg Stark Wavelets and signal processing // Springer International Publishing Switzerland. 2019. 254 р.

7. Гонсалес Р., Вудс Р. Цифровая обработка изображений. 3-е изд., доп. М.: Техносфера, 2012. 427 с.

8. Малла С. Вейвлеты в обработке сигналов. М.: Горячая линия – Телеком, 2015. 671 с.

Исследование выполнено за счет гранта Российского научного фонда № 23-21-00036, https://rscf.ru/project/23-21-00036/».

Проблема обеспечения доступа в любой точке Земли к информационным технологиям, которые предоставляет информационно-коммуникационная сеть Интернет, еще далека от своего решения. Поэтому в последнее десятилетие было предложено несколько глобальных проектов построения спутникового интернета [1]. Так как часть абонентов располагается за полярным кругом, то спутниковый интернет должен использовать низкоорбитальные космические аппараты (КА). В настоящее время была развернута низкоорбитальная система спутникового интернета (НССИ) StarLink. Для организации эффективной беспроводной связи, в том числе в районах Крайнего Севера, на орбиту было выведено более 2000 низкоорбитальных космических аппаратов [2, 3]. Чтобы обеспечить минимальную себестоимость развертывания беспроводной системы связи, а также высокую скорость обмена данными в системе StarLink, было решено использовать методы ортогонального частотного мультиплексирования (OFDM). Выбор данной технологии объясняется основными достоинствами, которыми она обладает. К ним, как правило, относят [4, 5]: высокий уровень спектральной эффективности; эффективную работу в условиях многолучевости; низкую межсимвольную интерференцию. Анализ становления технологии OFDM показывает, что основным драйвером ее развития является обеспечение более высокой скорости передачи информации. Для достижения данной цели разработчики предлагают уменьшить размер циклического префикса и корректирующие способности кода, увеличить разрядность QAM-модулятора, использовать метод МИМО. При этом вопросы снижения времени на цифровую обработку сигналов за счет замены быстрых ДПФ (БПФ) на целочисленные дискретные вейвлет-преобразования (ЦДВП), например ЦДВП Хаара, не были рассмотрены. При этом существует возможность повышения скорости вычислений ЦВП с целочисленных алгебраических систем – конечных полей Галуа. Поэтому применение алгебраической системы конечного поля при реализации математической модели ЦДВП Хаара является актуальной задачей.

В основе быстрых алгоритмов ДПФ лежит базовое преобразование «бабочка». Для ее выполнения спецпроцессору БПФ необходимо выполнить четыре операции умножения действительных и мнимых частей сигнала, а также шесть операций сложения. Переход к ЦВП Хаара позволяет уменьшить время на выполнение цифрового преобразования сигнала из частотной области во временную и обратно. Переход к более высокой производительности спецпроцессора ЦВП Хаара можно обеспечить за счет применения конечных полей Галуа. В этом случае операции сложения, вычитания и умножения можно заменить процедурами выборки результатов этих операций из LUT-таблиц. Цель исследований – уменьшить временные затраты на цифровую обработку сигналов в системах OFDM за счет использования математической модели модифицированного целочисленного вейвлет-преобразования Хаара, реализованного в конечном поле Галуа.

Материалы и методы исследования

Вейвлет-преобразования (ВП) широко применяются в областях, связанных с обработкой и анализом нестационарных сигналов [6–8]. Это вызвано тем, что полученные результаты обработки показывают не только распределение энергии сигнала по частотной области, но и связывают это с временным масштабом. В результате этого можно однозначно определить поведение определенных частотных составляющих сигнала. Отличительной особенностью ВП от ДПФ является то, что они генерируют двумерную развертку сигнала по времени и частоте, что позволяет проводить исследования сигнала сразу в двух измерениях. В этом случае при анализе сигнала строится ряд функций, являющихся базисом ВП с использованием операторов временного сдвига b и масштаба времени а,

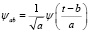. (1)

Данный ряд функций вычисляется с помощью первичного вейвлета ψ(t), который считается материнским. Используя эти вейвлет-функции ψab(t), можно получить вейвлет-образ сигнала s(t) с помощью выполнения интегрального ВП:

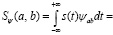
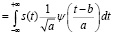. (2)

Идея вычисления интегрального ВП сигнала s(t) базируется на его разложении на масштабированные значения МВ, которые при этом будут сдвинуты во временной области. Для обратного восстановления сигнала с помощью его вейвлет-образов Sψ(a,b) необходимо воспользоваться нормализующим коэффициентом

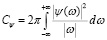. (3)

Тогда обратное ВП имеет вид

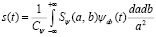. (4)

Очевидно, что скорость выполнения дискретного ВП зависит от количества коэффициентов, используемых в ВП. Наименьшее количество коэффициентов имеет вейвлет-преобразование Хаара [8]. В этом случае значения базисных функций Хаара hk(m) определяются на m ∈ [0,1]. Если k = 0, то имеем

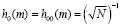. (5)

Для получения остальных базисных функций Хаара применяется равенство

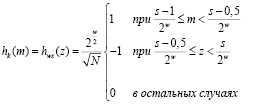, (6)

где w, s – индексы, которые задаются k = 0, 1, 2, … N – 1; N = 2L; m ∈ [0,1].

С помощью преобразования Хаара одномерный сигнал 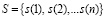, имеющий n отсчетов, можно представить двумя наборами коэффициентами. Первыми коэффициентами является аппроксимирующие 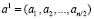, которые определяются

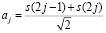, (7)

где j = 1, 2, …, n / 2.

Вторыми являются детализирующие коэффициенты 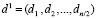, вида

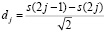, (8)

где j = 1, 2, …, n / 2.

Данное преобразование можно представить в виде базовой матрицы для обработки двух отсчетов

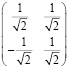. (9)

Как показано в [8], аппаратная реализация ДВП Хаара представляет собой набор двух цифровых фильтров. Первый фильтр будет низкочастотным. Его коэффициентами являются .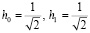

Второй фильтр является высокочастотным. Его коэффициентами фильтрации являются .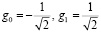

Используя базовую матрицу коэффициентов разложения (9), получаем модифицированное целочисленное преобразование Хаара. В этом случае матрица прямого преобразования имеет вид (10):

.

В результате данной модификации получается разложение входного сигнала, состоящего из восьми отсчетов на две части. Первая часть – это аппроксимирующие коэффициенты входного сигнала. Вторая часть – детализирующие коэффициенты входного сигнала. Тогда, используя дискретное вейвлет-преобразование Хаара (DWTH), получаем разложение сигнала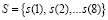

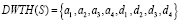.(11)

Анализ базовой матрицы (9), на основе которой реализуется ДВП, показывает, что коэффициенты Хаара – это иррациональные числа. В результате этого при обработке сигналов в системе OFDM с помощью ДВП Хаара, во-первых, не будут обеспечены минимальные временные затраты на реализацию данной процедуры. Во-вторых, в процессе вычислений будет происходить накапливание ошибок округления. Устранить данные недостатки можно за счет использования целочисленных дискретных вейвлет-преобразований (ЦДВП) Хаара, реализованных в конечном поле Галуа. Реализация ЦДВП в GF(p) позволит заменить выполнение операций сложения, вычитания и умножения операцией выборки из LUT-таблиц результатов. В результате будет сокращено время на ортогональное преобразование сигнала, что повысит скорость передачи информации.

Для реализации вычислений ЦДВП Хаара в поле GF(p) необходимо выполнить операцию масштабирования коэффициентов Хаара. Для этого используется коэффициент масштабирования D = 2n, где n = 1, 2, … В результате получаем целочисленные коэффициенты низкочастотные

.

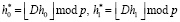Для высокочастотных коэффициентов Хаара имеем

,

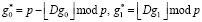которые становятся элементами поля Галуа. В этом случае матрица (9) будет иметь вид

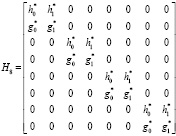.(12)

Так как среди коэффициентов Хаара есть отрицательные числа, то они будут располагаться во второй части диапазона от p/2 до p – 1. В этом случае отрицательное число – S будет представляться в виде .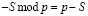

Результаты исследования и их обсуждение

Проведем сравнительный анализ модифицированного целочисленного вейвлет-преобразования Хаара, реализованного в конечных полях Галуа с БПФ. Исходные данные сигнала OFDM, используемого в НССИ [3]: размер созвездия – 64 QAM; размерность – 52 поднесущие; разрядность входного сигнала и коэффициентов Хаара – 8 бит; коэффициент масштабирования D = 256. В качестве характеристики поля Галуа выбираем простое число, которое удовлетворяет условию p > 217. Выбираем простое число p = 131101. Тогда целочисленные коэффициенты Хаара будут иметь вид

,

.

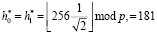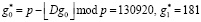Сравнительный анализ будем производить с 64-точечным БПФ. Данное преобразование реализуется за шесть итераций. На каждой итерации выполняется базовая процедура БПФ «бабочка». Рассмотрим реализацию целочисленного ДВП Хаара в конечном поле 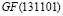. Пусть входной вектор S состоит из 16 отсчетов, представленных во втором столбце таблицы. В третьем столбце таблицы показаны 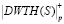– результаты выполнения целочисленного ДВП Хаара в поле GF(p). Четвертый столбец – масштабирование результатов с учетом D = 256. В пятом столбце показаны WTH(S) – результаты выполнения ДВП Хаара. В шестом столбце показаны 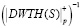– результаты выполнения обратного преобразования Хаара в поле GF(p). Седьмой столбец таблицы 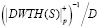– масштабирование результатов обратного преобразования с учетом D = 256. В восьмом столбце таблицы показаны (WTH)–1 – результаты выполнения обратного ДВП Хаара.

Анализ таблицы показывает, что результаты выполнения ДВП в различных алгебраических системах позволяют получить одинаковые результаты. В этом случае результаты масштабирования 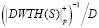необходимо в сторону большего целого числа.

Чтобы оценить эффективность предложенной модификации ДВП Хаара в полк GF(р), было проведено RTL моделирование. Данное моделирование осуществлялось на ПЛИС Kintex 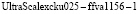с использованием Xilinx Vivado-HLS 2018. Временные затраты на выполнение модифицированного ЦДВП Хаара в GF(p) при ортогональной обработке сигнала составили с учетом умножения на отрицательный коэффициент и операции обратного масштабирования составили 310 нс. При этом на реализацию БПФ потребовалось 468 нс.

Реализация ДВП Хаара в алгебраических системах

Таким образом, использование разработанной математической модели модифицированного ЦДВП Хаара в поле Галуа позволило сократить временные затраты на обработку сигнала в 1,51 раза, что обеспечит повышение скорости передачи сигналов в системах OFDM, используемых в НССИ.

Заключение

В статье рассмотрен один из подходов, позволяющий повысить скорость передачи информации в системах OFDM. Данный подход основан на замене БПФ на модифицированное ЦДВП Хаара в GF(p) при выполнении ортогональных преобразований сигналов. Проведенное моделирование с использованием ПЛИС Kintex 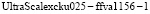с использованием Xilinx Vivado-HLS 2018. Временные затраты на выполнение модифицированного ЦДВП Хаара в GF(p) при ортогональной обработке сигнала составили с учетом умножения на отрицательный коэффициент и операции обратного масштабирования составили 310 нс. При этом на реализацию БПФ потребовалось 468 нс. Таким образом, использование разработанной математической модели модифицированного ЦДВП Хаара в поле Галуа позволило сократить временные затраты на обработку сигнала в 1,51 раза, что обеспечит повышение скорости передачи сигналов в системах OFDM, используемых в НССИ. Поставленная в статье цель достигнута.

Библиографическая ссылка