Как было показано ранее [1-3], конструкция тихоходных длинноходовых ступеней поршневых компрессоров позволяет, по сравнению с быстроходными аналогами, существенно снизить влияние мертвого объёма на рабочий процесс за счёт увеличения соотношения величины хода поршня и диаметра цлиндра. При этом режим работы длинноходовых агрегатов (длительное время рабочего цикла) обеспечивает интенсивное охлаждение сжимаемого газа и низкую температуру нагнетания даже при повышенных соотношениях давлений нагнетания и всасывания в ступени [4-6]; реализация такого рабочего процесса невозможна в современных быстроходных поршневых ступенях, где время рабочего цикла составляет сотые доли секунды [7-9]. Проведённые ранее исследования рабочих процессов тихоходных длинноходовых компрессорных ступеней определили как одно из основных направлений их совершенствования снижение утечек через неплотности рабочей камеры, в том числе за счёт применения в конструкции самодействующих клапанов деформируемых эластомерных элементов [10; 11]. Применение деформируемого эластомерного конструкционного элемента позволяет в том числе изменять периметр щелевого зазора в седле клапана по сравнению с номинальным, увеличивая его герметичность при сохранении пропускной способности в открытом состоянии [11]. Этот фактор может оказать заметное влияние на эффективность рабочего процесса компрессорной ступени. В связи с этим актуальным становится вопрос уточнения методики расчёта рабочего процесса тихоходных длинноходовых ступеней поршневых компрессоров с деформируемым эластомерным элементом, входящим в конструкцию самодействующего клапана.
Объектом исследования является поршневая тихоходная длинноходовая компрессорная ступень, подробно описанная, например, в [1; 12], отличительной особенностью которой являются клапаны, содержащие деформируемые эластомерные элементы. Рассмотрены клапаны со следующими основными параметрами: номинальный диаметр проходного сечения в седле 0,003 м; высота подъёма запорного органа h = 0,001 м; величина деформации эластомерного элемента hэл = 0,0006 м; приведённая сила упругости пружины для всасывающего клапана 3500 Н/м, для нагнетательного клапана 30 000 Н/м. Параметры ступени: температура газа на всасывании 290 К, давление всасывания 0,1 МПа, давление нагнетания до 10,0 МПа, диаметр цилиндра 0,05 м; ход поршня 0,5 м; время рабочего цикла 2…4 с.
Целью исследования является уточнить существующую методику расчёта рабочих процессов тихоходных поршневых компрессорных ступеней в части моделирования динамики клапана с деформируемым эластомерным элементом и изменения периметра зазора в контакте между запорным органом и седлом.
Принципиальная схема клапана с эластомерным элементом (в открытом (а) и закрытом (б) положении) представлена на рисунке 1.
Методика экспериментального исследования ступени
Схема экспериментальной тихоходной длинноходовой ступени поршневого компрессора с линейным гидроприводом представлена на рисунке 2; общий вид экспериментального стенда [12; 13] – на рисунке 3. При работе гидростанция 1 подаёт рабочую жидкость в гидроцилиндр 2, обеспечивая возвратно-поступательное движение штока 3, жестко закрепленного на штоке компрессора 4. Уплотнения 5, установленные на поршне компрессорной ступени, выполнены из самосмазывающихся материалов. Органы газораспределения (клапаны всасывания 6 и нагнетания 7) установлены во втулке 8. Цифровой запоминающий осциллограф 9 производит сбор и сохранение изменяющихся параметров. Датчики давления 10 и температуры 11 фиксируют изменение параметров состояния газа в рабочей камере. Для измерения быстроизменяющегося давления газа в рабочей камере ступени использовались кремниевые датчики давления типа Д16 [13].
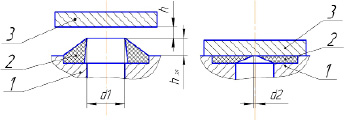
а) б)
Рис. 1. Схема открытого и закрытого клапана с эластомерным элементом: а) открытый клапан; б) закрытый клапан; 1 – запорный орган; 2 – эластомерный элемент; 3 – седло клапана
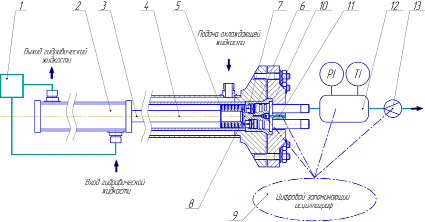
Рис. 2. Схема тихоходной длинноходовой ступени поршневого компрессора с линейным гидроприводом: 1 – гидростанция; 2 – гидроцилиндр; 3 – шток гидроцилиндра; 4 – шток компрессора; 5 – уплотнения цилиндро-поршневой группы; 6 – клапан всасывания; 7 – клапан нагнетания; 8 – клапанная втулка; 9 – цифровой запоминающий осциллограф; 10 – датчик давления; 11 – датчик температуры; 12 – ресивер; 13 – расходомер

Рис. 3. Общий вид экспериментального стенда
Приборная погрешность при тарировке датчика давления определяется по формуле [14-16]:
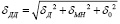 , (1)
, (1)
где δД – относительная погрешность датчика давления, %; δМН – относительная погрешность образцового манометра, %; δ0 – относительная погрешность осциллографа, %.
Здесь относительная погрешность датчика давления принимается согласно паспортным данным δД = 1,4%, соответственно также принимается относительная погрешность образцового манометра δМН = 1,5% и относительная погрешность осциллографа δ0 = 3%.
Тогда общая погрешность датчика давления равна:
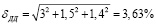 .
.
Определим общую погрешность датчика температуры – бусинкового термистора [15]:
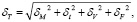 (2)
(2)
где δМ – относительная погрешность осциллографа, 0,05%;
δt – погрешность термометра, определяемая погрешностью прибора, 0,1%;
δV – погрешность вольтметра, определяемая погрешностью прибора, 0,3%;
δF – погрешность расчёта по полученной интерполированной формуле, 1,5%.
Тогда
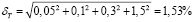 .
.
Для измерения расхода применялся датчик типа AWM720P1 фирмы Honeywell. Погрешность данного датчика составляет 2%.
Методика расчёта
Математическая модель рабочих процессов подробно описана в работах [17-19]. В систему основных расчётных уравнений рабочего процесса тихоходной длинноходовой поршневой компрессорной ступени входят: первый закон термодинамики для тела с переменной массой, уравнение состояния, уравнение массового баланса, следствие закона Джоуля для внутренней энергии газа, уравнения расхода газа через клапаны (в открытом и закрытом состоянии) и через зазоры в цилиндро-поршневой группе, уравнение конвективного теплообмена между газом и стенками рабочей камеры.
Исходные данные для расчета: температура всасывания; давление нагнетания и давление всасывания; газовая постоянная; теплофизические свойства газа; диаметр цилиндра; ход поршня; величина мертвого объема; частота рабочего цикла. Выходные данные результатов расчета: текущие параметры состояния газа в рабочей камере; масса газа в рабочей камере, тепловые и массовые потоки, а также интегральные характеристики ступени. Расчетная схема, условия однозначности и основные допущения подробно представлены в [19]. Система уравнений решается численно, методом конечных разностей, при разработке алгоритма был применен метод Эйлера второго порядка точности.
В качестве уточнения в данную методику в выражение для расчёта массового потока газа через закрытый клапан [4; 5; 8] вводится изменяемая величина периметра прилегания запорного органа к седлу (π·D(hi)):
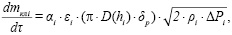 (3)
(3)
где mклi – масса газа, проходящая через закрывающийся или открывающийся клапан, кг; ai – коэффициент расхода; εi – коэффициент расширения газа; ΔPi – разность давлений газа до и после клапана или щели, Па; δр – условный зазор в клапане, м; ρi – плотность газа перед клапаном или щелью, кг/м3; D(hi) – изменяемый при деформации эластомерного элемента диаметр седла, м.
Уравнение динамики запорного органа также изменяется, так как появляется дополнительная сила упругости, действующая со стороны эластомерного элемента:
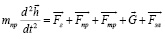 (4)
(4)
где Fг, – суммарная сила, действующая на пластину со стороны газа, Н; Fпр – сила упругости пружины, Н; Fтр – сила трения газа, Н; Fэл – сила упругости эластомерного элемента; G – вес запорного органа.
Расчетная методика определения деформаций эластомерного элемента самодействующего клапана
Модель работы эластомерного элемента в самодействующем клапане реализована в программном комплексе ANSYS Workbench Mechanical [6; 10]. Используемая программа позволяет вычислить изменение геометрии эластомерного элемента при его деформации. При расчёте использовались следующие данные. Материал седла и пластины (запорный орган) – сталь 40Х (7850 – плотность, кг/м3; 2,0·1011 – модуль упругости, МПа; 0,3 – коэффициент Пуассона), материал эластомерного элемента – резина (1000 – плотность, кг/м3; 7 – модуль упругости, МПа; 0,49 – коэффициент Пуассона).
На рисунке 4 представлена 3D-модель рассматриваемого самодействующего клапана с примером расчётной сетки.
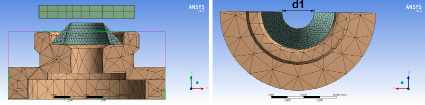
Рис. 4. Расчётная сетка конечных элементов
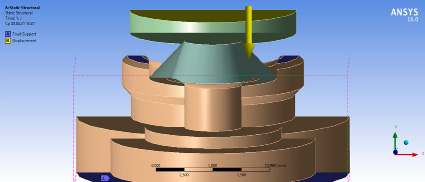
Рис. 5. Условия закрепления
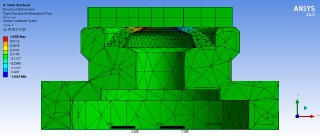
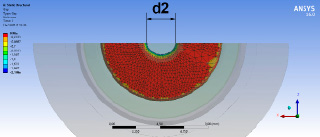
Рис. 6. Деформированное состояние эластомерного элемента клапана
Для моделирования взаимодействия между деталями используется настройка контактов (Connections → Contacts). Поскольку данный клапан устанавливается в клапанную плиту, то по нижней части седла принимается условие закрепления как неподвижное. Для запорного органа (пластина) устанавливается перемещение 1,6 мм, до полного прилегания пластины к седлу (рис. 5).
Полученные результаты по уменьшению периметра зазора для рассматриваемых профилей эластомерных элементов представлены на рисунке 6.
Полученные результаты показали возможность уменьшения периметра в закрытом клапане с деформируемым эластомерным элементом. На рисунках 4, 6 имеет место очевидное уменьшение диаметра отверстия в эластомерном элементе; для рассмотренной конфигурации эластомерного элемента уменьшение периметра может составить до 40% по сравнению с номинальным.
Результаты исследования и их обсуждение
По результатам выполненных исследований была проведена сравнительная оценка экспериментальных и теоретических результатов, в качестве которых рассматривались зависимости коэффициента подачи и индикаторного изотермического КПД от степени повышения давления в ступени (рис. 7, 8).
Нужно заметить, что для клапана с эластомерным элементом расстояние от седла до запорного элемента больше на величину высоты конуса эластомера (рис. 1) и в данном случае составляет 0,6 мм. При этом в расчётной методике деформация может быть учтена следующим образом:
при 1,6 ˂ h ˂ 0,6, D(hi) = d1;
при 0,6 ˂ h ˂ 0,
D(hi) = –0,0019·h3 + 0,0069·h2 – 0,0017·h + 0,00195;
при h = 0, D(hi) = d2.
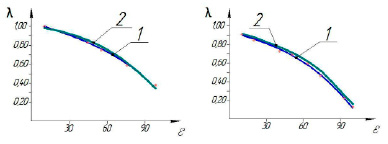
а) б)
Рис. 7. Зависимость коэффициента подачи от степени повышения давления: а) при времени цикла 2 с: 1 – эксперимент; 2 – теория; б) при времени цикла 4 с: 1 – эксперимент; 2 – теория
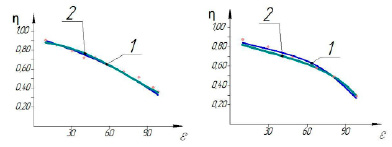
а) б)
Рис. 8. Зависимость индикаторного изотермического КПД от степени повышения давления: а) при времени цикла 2 с: 1 – эксперимент; 2 – теория; б) при времени цикла 4 с: 1 – эксперимент; 2 – теория
Сравнение полученных теоретических и экспериментальных результатов показало полное качественное и удовлетворительное количественное соответствие (расхождение расчётных и экспериментальных результатов составило не более 6%). Применение клапана с деформируемым эластомерным элементом позволило увеличить коэффициент подачи примерно на 10%, а изотермический индикаторный КПД – на 12% (сравнение проводилось с полученными ранее интегральными характеристиками наиболее близких аналогов тихоходной компрессорной ступени [4; 5]). Важно отметить, что применение неметаллических конструкционных материалов, в том числе эластомеров, в рассматриваемых компрессорных ступенях становится возможным из-за низких температур нагнетаемого газа, обусловленных интенсивным теплоотводом в процессе сжатия и нагнетания [11; 19].
Выводы
Таким образом, проведённые исследования позволили уточнить существующую методику расчёта рабочих процессов тихоходных поршневых компрессорных ступеней в части моделирования динамики клапана с деформируемым эластомерным элементом и изменения периметра зазора в контакте между запорным органом и седлом. Несмотря на то что в данном исследовании был рассмотрен частный случай конструкции клапана с деформируемым элементом, можно предположить, что последующая оптимизация геометрии эластомерного элемента и подбор перспективных материалов в качестве эластомерных элементов позволят обеспечить повышение энергетической эффективности рассматриваемой ступени не менее чем на 10% и прогнозируемый ресурс не менее 25 000 часов.
Библиографическая ссылка
Бусаров И.С., Карагусов В.И., Кобыльский Р.Э., Бусарова Ю.Д. ВЕРИФИКАЦИЯ МЕТОДИКИ РАСЧЕТА РАБОЧИХ ПРОЦЕССОВ ДЛИННОХОДОВЫХ БЕССМАЗОЧНЫХ ПОРШНЕВЫХ КОМПРЕССОРНЫХ СТУПЕНЕЙ С САМОДЕЙСТВУЮЩИМ ЭЛАСТОМЕРНЫМ КЛАПАНОМ // Современные наукоемкие технологии. 2023. № 3. С. 15-21;URL: https://top-technologies.ru/ru/article/view?id=39549 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.39549



