История возникновения термина «вычислительное мышление восходит к 220 г. до н.э., когда Архимед, используя методы вычислительной математики, получил двухстороннюю оценку для числа π. Таких примеров можно привести достаточно много, Их роднит то, что вычисления начались с осознанной потребности человека в получении приближенных методов решения насущных задач (геометрических вычислений, а также потребностей механики, физики, химии и других областей науки и техники). Вычислительная математика смогла обеспечить возможность человеку «…манипулировать цифровыми представлениями и моделями… все люди в какой-то мере занимаются вычислительным мышлением уже в повседневной жизни…» [1].
В технических вузах численные методы изучаются в виде отдельных глав при изучении высшей математики, математического моделирования, методов оптимизации. Этот подход закреплен в рекомендациях Европейского общества инженерного образования (SEFI) в документе «Математика для европейского инженера» [2]. В большинстве российских технических вузов предмет «Численные методы» является самостоятельным и читается на втором курсе.
Говоря о дисциплине «Численные методы», следует отметить, что она является основной в подготовке специалистов в области вычислительной математики, а также физики и информатики в классических и педагогических университетах. В современных условиях, когда Россия столкнулась с необходимостью отстаивания собственного технологического суверенитета, существенно возрастает роль инженера как носителя технологической культуры. Только на основе возрождения лучших образцов инженерных школ, базирующихся на фундаментальной подготовке в области математики и, в частности развитом вычислительном мышлении, Россия сможет доказать свою состоятельность и технологическую независимость [3]. Поэтому целью исследования является описание феномена «вычислительное мышление инженера» и анализ опыта его формирования в процессе профессиональной подготовки.
Материалы и методы исследования
Методами исследования являлись: понятийно-терминологический анализ нормативных документов, контент-анализ рабочих программ, сравнительно-сопоставительный анализ педагогического опыта.
В нормативной базе ФГОС ВО [4] в качестве формируемых в образовательной деятельности вузов компетенций специалистов по направлению 09.03.01 Информатика и вычислительная техника (далее соответственно – программа бакалавриата, направление подготовки) присутствуют компетенции, реализуемые с помощью вычислительного мышления: УК-1. Способен осуществлять поиск, критический анализ и синтез информации, применять системный подход для решения поставленных задач; ОПК-1. Способен применять естественнонаучные и общеинженерные знания, методы математического анализа и моделирования, теоретического и экспериментального исследования в профессиональной деятельности.
Мы разделяем методологию проектирования целей инженерного образования, основанную на положениях личностно-деятельностного подхода (Б.Г. Ананьев, П.Я. Гальперин, Н.Ф. Талызина и др.), культурологического подхода (Е.В. Бондаревская, И.Я. Лернер, С.В. Кульневич и др.), а также личностно-ориентированного подхода (Н.А. Алексеев, В.В. Сериков, И.С. Якиманская и др.) согласно которым цели инженерного образования проектируются сообразно целям инженерной деятельности, а личность будущего инженера рассматривается как ценностное ядро системы образования.
Каковы цели инженерной деятельности на сегодняшнем культурно-историческом и технико-экономическом этапе развития России? Наиболее полно эти цели отражены в понятии «инжиниринг», в классической трактовке, приведенной в издании «Britannika» [5]: «применение науки к оптимальному преобразованию ресурсов природы для нужд человечества... осознанное применение научных принципов проектирования или разработки конструкций, машин, аппаратов или производственных процессов, или работ, использующих их по отдельности или в комбинации; создание и использование их с полным пониманием их конструкции... в отношении предполагаемой функции, экономичности эксплуатации и безопасности». Иногда термин «инжиниринг» определяется более свободно, как «производство или сборка двигателей, станков и деталей машин». Основными функциями инжиниринга являются исследовательская деятельность – поиск новых принципов и процессов с использованием математических и научных концепций, экспериментальных методов и принципов индукции (курсив авт.), – и генерация новых знаний.
Следует отметить, что существует упрощенное понимание инжиниринга, под которым понимаются технические консультационные услуги, связанные с разработкой и подготовкой производственного процесса и обеспечением нормального хода процесса производства и реализации продукции [6]. Такой поверхностный подход считаем неприемлемым, поскольку он уже оказал негативное влияние на результат инженерной подготовки в вузах и, как следствие – на утрату технологического суверенитета России [7].
Поскольку современный инженерный вуз нацелен на подготовку квалифицированного инженера в любой отрасли технического знания, то круг задач по подготовке такого специалиста существенно расширен [3]. От современного инженера, обладающего системными знаниями – назовем его системным инженером, – требуется проектирование нового объекта (инженерного продукта), когда системы еще нет. Необходимо отдельные элементы новой, пока еще только создаваемой, системы, физические и другие свойства которой в неявном виде представлены разными инженерными знаниями, объединить в безотказно работающую модель, нужно по отдельным частям воссоздать образ нового на основе общих связей и отношений [8, 9]. Также необходим анализ возможных рисков и неудач от взаимовлияния различных частей сложной инженерной системы, а также надежные алгоритмы отладки ошибочных проб. Причем время и финансовые затраты на такие алгоритмы не могут быть бесконечны, их необходимо минимизировать. Необходим прогноз дальнейшей работы механизма, как связной системы. Современные инженерные задачи, относящиеся к разделам механики, физики твердого тела, материаловедения решаются с помощью систем твердотельного или 3D-моделирования. Например, пакеты SolidWorks, Solid Edge, Marc 3D, «КОМПАС 3D + ВЕРТИКАЛЬ» и аналогичные создают, с применением разностных схем, приближенное решение, используя моделирование на сетках. Системы предлагают пользователю набор готовых шаблонов решений, описываемых системой дифференциальных уравнений. Инженер должен, с большей или меньшей степенью детализации, описать поведение системы в узлах пространственной сети. Затем, используя возможности вычислительных методов, система «достраивает» решение до конечного требуемого результата. Получается твердотельная модель технической системы, описывающая ее с достаточной степенью точности. Необходимую возможность описания и конструирования новой технической системы представляет отдельная область математики – численные методы.
Результаты исследования и их обсуждение
Обратимся к этимологии термина. Сам термин вычислительное мышление был впервые использован Сеймуром Пейпертом в 1980 г. и повторно был использован им в 1996 г. Особый интерес к этому понятию в 2006 г. проявила Жаннетта Винг, профессор Питсбургского университета Карнеги-Меллона. С ее точки зрения [10], вычислительное мышление – это фундаментальное умение для понимания жизни и ее развития в современном мире, необходимое для решения задач, проектирования систем и понимания человеческого поведения с помощь понятий, фундаментальных для информатики: «Это абстракция, которая может быть автоматизирована, и это то, чем занимаются вычисления». Здесь видны три основных структурных элемента вычислительного мышления: (1) абстракция – формулировка проблемы; (2) автоматизация – представление решения в виде алгоритма; (3) анализ – исполнение и оценка (рефлексия) результата.
Соотношение мышления и объекта в данном случае выстроено на основе парадигмы: «Если я хочу познать данное мне Все, то как я это могу сделать?» [11]. Для того, чтобы инженеру сформировать и самостоятельно развивать вычислительное мышление, ему необходимо понимание сути самих чисел, а также умение сопоставлять эти числа с логическими операции над ними, то есть, по сути, разрабатывать некий алгоритм решения задачи для создания технической конструкции нового инженерного продукта. Вычислительная математика в данном случае должна заменить рутинные функции человека.
Как связаны численные методы и вычислительное мышление будущего специалиста и какими свойствами должно обладать вычислительное мышление?
Психологи выделяют три вида мышления [12]: предметно-действенное (практическое), конкретно-образное и абстрактное. Инженер по роду своей деятельности мыслит и образно и абстрактно. Сравнительный анализ исследований [1, 12, 13] позволяет утверждать, что ему присущи свойства алгоритма: дискретность, определенность, результативность, массовость. Не останавливаясь подробно на каждом из них, отметим, что для инженерной деятельности наиболее важными являются последние два.
В чем заключается дидактический потенциал дисциплины «Численные методы» в среде технического вуза? Общепринятыми функциями методической среды инженерного вуза являются: организационная, методологическая и информационная. Они реализуются на занятиях лекционного типа.
Проведенный авторами контентный анализ рабочих программ дает право утверждать, что методология и методика преподавания дисциплины «Численные методы» для разных направлений подготовки инженеров существенно различаются. Поскольку для технического специалиста – инженера – важна реальная профессиональная задача, для которой он должен подобрать наиболее эффективный метод решения, то акцент следует делать на практических занятиях, показывая типовые расчетные и проектные процедуры, не раскрывая особенности их реализации. Исследователями, например Т.А. Степановой [14], предложены два «параллельных способа обучения», повышающие роль самостоятельной работы и создающие условия для освоения материала в сжатые сроки. Первый подход предполагает деление предметной части на классы эквивалентности, что позволяет распределить такие монозадания между студентами и организовать публичную защиту решений. Второй предусматривает возможность применения проектного подхода – формирование рабочей группы и декомпозиция комплексной задачи на несколько монозадач. Какой из способов обучения выбрать – решает преподаватель исходя из возможностей темы (декомпозиции материала на логически связанные части), возможностей студентов, их индивидуальных психологических характеристик, а также наличия соответствующей вычислительной базы.
Отметим особенности дидактической и методической работы по результатам опыта преподавания предмета «Численные методы». Всего исследование охватило более 200 чел. по двум направлениям подготовки «Программная инженерия» и «САПР».
На начальном этапе обучения целесообразно применение первого подхода, при котором активация ментальных схем, связанных с решением каждой конкретной задачи индуцируется и поддерживается преподавателем. Каждый элемент построенной ментальной цепи может быть как ранее сформированным, например, на занятиях по предметам «Математический анализ», «Линейная алгебра» и «Программирование», а может быть субъективно новым – являющимся неизвестным отображением новой математической реальности. Очень полезным дидактическим подспорьем явился разработанный авторами методический комплекс «Элементы вычислительной математики», включающий в себя теоретические материалы по пяти основным разделам (системы линейных уравнений, итерационные методы для нелинейных уравнений, нелинейные системы, численное интегрирование, задача Коши для обыкновенных дифференциальных уравнений). Комплекс содержит материалы практических занятий, где отрабатываются основные навыки вычислений и заканчиваются заданиями на проведение лабораторных работ, вопросами к отчету по лабораторным работам и рекомендациями по составлению протокола. Каждый студент имеет возможность предварительного знакомства с материалами теории и практики еще до проведения соответствующего занятия. Учебное пособие снабжено глоссарием и ссылками на обширную литературу, что благоприятно сказывается на углубленном изучении новой и актуализации ранее полученной информации. Лекционные и практические занятия проводятся парами переменного состава, как правило, это два наиболее квалифицированных преподавателя кафедры. Ранее эти же преподаватели читали курсы математического анализа, линейной алгебры и аналитической геометрии и акцентировали внимание студентов на вычислительных аспектах инженерных задач.
Приведем пример, иллюстрирующий данную дидактическую стратегию. При изучении темы «Нахождение собственных векторов и собственных значений, спектрального радиуса матрицы» студентам была предоставлена информация из соответствующего раздела «Линейной алгебры». Следует отметить алгоритм изучения тем. Он был выстроен в виде триады учебного комплекса: лекции – практические занятия – лабораторные работы. На лекции были актуализированы знания, связанные с нахождением характеристического многочлена, собственных чисел и собственных значений методом непосредственного развертывания, методом Крылова и методом Данилевского. Вопросы решения соответственно линейных однородных систем приближенными методами были подробно рассмотрены на практическом занятии. Аналогично был рассмотрен алгоритм нахождения матрицы поворота в методе Данилевского. В лабораторной работе (рисунок) студентам предлагалось найти соответственно собственные значения тремя предложенными способами и самостоятельно оценить трудоемкость и точность каждого из них.
После проведенного критического анализа предложенных методов студентам было предложено самостоятельно, в составе мини-групп из трех человек, выбрать алгоритм наиболее быстрый и удобный с точки зрения написания программы на языке С++ (C#).
Группа распределила роли в соответствии с функционалом вычислительных компетенций: консультирование и использование фундаментальных знаний в области численных методов (теоретик), реализация метода с помощью компьютерной программы (программист) и проведение сравнительного анализа алгоритмов, условий применимости и точности решений (аналитик). Коротко отметим, что функциональные роли участников группы не были инициированы педагогом, а явились следствием саморефлексии студентов. Установлено, что выбор программных средств достаточно важен, так как определяет стратегию информационного и математического сопровождения профессиональной траектории студентов на старших курсах и в практической деятельности. Именно поэтому для студентов инженерного направления полезно при изучении численных методов использовать языки программирования общего назначения, освоенные на 1…2 курсах в общеобразовательных дисциплинах.
а) 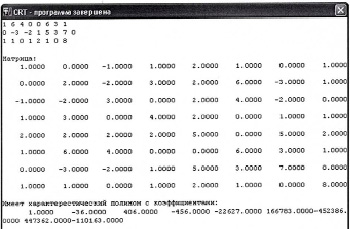
б) 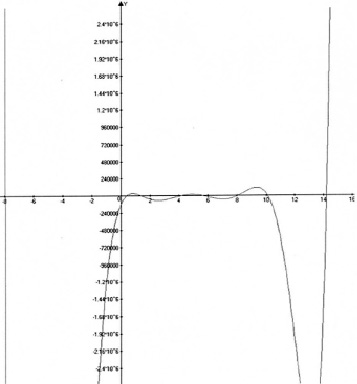
Таблица значений (а) и корни (б) характеристического полинома
Исходя из вышеназванных функций вычислительного мышления выделяются соответственно стратегии его формирования: алгоритмизации – четкое определение последовательности вычислительных действий, абстрагирования – способности выделять главное, без ущерба для основного смысла решения задачи; декомпозиции – фрагментация задач и алгоритмов на отдельные смысловые части, которые поняты и приняты всеми участниками группы; обобщения – выявление общих черт структуры и алгоритмов ранее решенных задач и качественно новых с последующей адаптацией полученного алгоритма на класс потенциально возможных задач; рефлексия – установление качества постановки задачи и алгоритма ее решения.
На основе анализа проведенной методической работы был выдвинут комплекс дидактических условий, среди которых наиболее значимыми являются:
1. Активизация познавательной активности путем включения задач, отражающих многообразие выбора способов решения и неоднозначность достигнутого результата.
2. Учет влияния индивидуальных особенностей, психологических возможностей студентов на широту и темп предоставления теоретического материала и практических заданий.
3. Возможности современных информационно-коммуникативных технологий и вычислительной математики, программного обеспечения.
4. Формирование ценностной установки на совместную, командную деятельность.
5. Участие самих студентов в подборе, решении профессионально значимых задач и создании коллективно-распределенной среды, имитирующей будущую инженерную деятельность.
6. Выход в квазипрофессиональные среды, участие в проектной деятельности.
Заключение
Сделаем некоторые выводы по результатам проведенной работы. Вычислительное мышление является своего рода связующим звеном между вычислительной математикой и инжинирингом. Оно может быть применимо к различным техническим и общеобразовательным дисциплинам. Однако наиболее логично и целесообразно его развитие в инженерном вузе происходит на материале курса «Численные методы». Содержание курса «Численные методы» является достаточно эклектичным, а потому сложным для освоения. Целесообразно инъективное включение элементов курса «Численные методы», например, в разделы специальных глав математики, которые могут быть прочитаны на старших курсах бакалавриата, специалитета или магистратуры. Существенное значение для выбора содержания имеют ранее сформированные знания и навыки самостоятельной и командной работы студентов, а также опыт решения проектных задач, содержание которых зависит от направления подготовки инженеров. Необходимо использовать возможности смешанного обучения с использованием современных информационных технологий. Целесообразен переход от педагогического сопровождения на младших курсах к сопровождению математическому на этапе профессиональной подготовки будущего инженера. Под математическим сопровождением в данном случае понимается совместная работа преподавателя математики со студентом старших курсов (или с уже состоявшимся специалистом, выпускником университета), успешно завершившим изучение математических дисциплин естественнонаучного блока. Необходимость в таком сотрудничестве возникает при включении студентов старших курсов в профессиональную инженерную деятельность, связанную с применением математических методов для решения инженерных задач. Подобное математическое сопровождение описано в работе [6]. Для инженеров, включенных в творческую инженерную деятельность, как правило, недостаточно использовать алгоритмы и методы, «зашитые» в распространенные CAD/CAM/CAE системы. На этом уровне инженерной деятельности требуется адаптация широко применяемых систем (разработка новых) – этот процесс связан с необходимостью выбора рациональных математических методов, т.е. от инженера требуется вычислительное мышление. Для успешного решения таких задач используется не педагогическое, как на младших курсах, а именно математическое сопровождение.
Библиографическая ссылка
Чигиринская Н.В., Григорьева О.Е., Бочкин А.М., Андреева М.И. ВЫЧИСЛИТЕЛЬНОЕ МЫШЛЕНИЕ БУДУЩЕГО ИНЖЕНЕРА: ПОНЯТИЙНЫЙ АНАЛИЗ И ОПЫТ ФОРМИРОВАНИЯ В ТЕХНИЧЕСКОМ ВУЗЕ // Современные наукоемкие технологии. 2023. № 2. С. 205-211;URL: https://top-technologies.ru/ru/article/view?id=39546 (дата обращения: 11.03.2026).
DOI: https://doi.org/10.17513/snt.39546



