Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ромм Я.Е. 1 Джанунц Г.А. 1

---

1 Таганрогский институт имени А.П. Чехова (филиал) ФГБОУ ВО «Ростовский государственный экономический университет (РИНХ)»

Описывается численное моделирование положения навигационного космического аппарата системы ГЛОНАСС по оперативной эфемеридной информации из навигационного сообщения. Моделирование реализовано на основе кусочно-интерполяционного решения задачи Коши для обыкновенных дифференциальных уравнений применительно к движению центра масс аппарата. Координаты и составляющие вектора скорости центра масс в произвольно заданные моменты времени из 30-минутного интервала прогнозирования предложенный метод дает с превышением требуемой точности, при этом время расчета существенно меньше времени расчета на основе метода Рунге – Кутты 4-го порядка. Кусочно-интерполяционное приближение решения задачи Коши непрерывно на всем интервале прогнозирования, аналогично непрерывно приближение его производной. Приближение равномерно сходится к решению задачи Коши, аналогично сходится приближение производной. На каждом подынтервале разбиения интервала прогнозирования полином, интерполирующий компонент решения, имеет вид алгебраического полинома фиксированной степени с числовыми коэффициентами. Это позволяет сохранять в памяти компьютера приближение компонента решения в виде типизированного файла (или массива) из коэффициентов полиномов, соответственных подынтервалам разбиения. Непрерывное приближение каждого компонента решения оказывается хранимым и восстанавливается без повторного решения задачи в произвольной точке интервала прогнозирования как соответственное значение полинома. На этой основе процесс прогнозирования естественным образом архивируется. Создаются предпосылки прогнозирования не отдельных точек траектории движения аппарата, а всего непрерывного отрезка этой траектории на интервале прогнозирования. Предложенный метод реализован в виде процедуры с параметрами, определяемыми из навигационного сообщения, и может быть автоматизирован. Приводится программный код процедуры, описываются результаты численного эксперимента.

Статья в формате PDF

512 KB

численное моделирование положения навигационного космического аппарата

расчет значений координат и составляющих вектора скорости центра масс

хранимое непрерывное приближение решения задачи Коши для дифференциальной модели

1. ГЛОНАСС. Интерфейсный контрольный документ. Общее описание системы с кодовым разделением сигналов. Редакция 1.0. 2016. Сайт ОАО «Российские космические системы». [Электронный ресурс]. URL: http://russianspacesystems.ru/wp-content/uploads/2016/08/IKD.-Obshh.-opis.-Red.-1.0-2016.pdf (дата обращения: 08.01.2023).

2. Maciuk K. Different approaches in GLONASS orbit computation from broadcast ephemeris. Geodetski vestnik. 2016. No. 60. P. 437–448. DOI:10.15292/geodetski-vestnik.2016.03.437-448.

3. RINEX – The Receiver Independent Exchange Format – Version 3.03. 14 July 2015 (IGS RINEX WG. RTCM-SC104. Pasadena 2015). [Электронный ресурс]. URL: https://files.igs.org/pub/data/format/ rinex303.pdf (дата обращения: 01.02.2023).

4. FTP архив прикладного потребительского центра государственной корпорации «Роскосмос». [Электронный ресурс]. URL: https://glonass-iac.ru/ftparchive/ (дата обращения: 08.01.2023).

5. Ромм Я.Е., Джанунц Г.А. О воспроизводимости функций, производных и решений дифференциальных уравнений с помощью хранимых коэффициентов кусочной интерполяции // Современные наукоемкие технологии. № 1. 2023. С. 44–63. DOI: 10.17513/snt.39497.

6. Джанунц Г.А., Ромм Я.Е. Варьируемое кусочно-интерполяционное решение задачи Коши для обыкновенных дифференциальных уравнений с итерационным уточнением // Журнал вычислительной математики и математической физики. 2017. Т. 57. № 10. С. 1641–1660.

7. Авдюшев В.А. Эффективные методы численного моделирования околопланетной орбитальной динамики: дис. … докт. физ.-мат. наук. Томск, 2010. 210 с.

8. Белянко Е.А., Краснопольский И.А., Михайлов М.В. и др. Метод повышения точности и «времени жизни» эфемерид ГЛОНАСС // Космонавтика и ракетостроение. 2011. № 4 (65). С. 111–121.

9. Ромм Я.Е., Джанунц Г.А. Кусочная интерполяция функций, производных и интегралов с приложением к решению обыкновенных дифференциальных уравнений // Современные наукоемкие технологии. № 12-2. 2020. С. 291–316. DOI: 10.17513/snt.38448.

10. ГЛОНАСС. Интерфейсный контрольный документ. Система высокоточного определения эфемерид и временных поправок. Редакция 3.0. 2011. Сайт ПМК СВОЭВП. URL: http://www.glonass-svoevp.ru/DATA/Documents/IKD_SVO.pdf. (дата обращения: 03.02.2023).

11. Dach R., Lutz S., Walser P., Fridez P. (Eds). Bernese GNSS Software Version 5.2. User manual, Astronomical Institute. University of Bern. Bern Open Publishing. 2015. DOI: 10.7892/boris.72297.

Для идентификации своего местоположения и скорости объект, использующий глобальную навигационную спутниковую систему (ГЛОНАСС), принимает радиосигналы не менее чем от 3–4 навигационных космических аппаратов (НКА), выполняет беззапросные измерения псевдодальности и радиальной псевдоскорости относительно каждого НКА, а также прием и обработку сообщения, содержащегося в составе навигационных радиосигналов [1]. В навигационном сообщении описывается положение НКА в пространстве и времени. Эфемериды спутников ГЛОНАСС обновляются каждые 30 минут. В результате обработки полученных измерений и данных навигационного сообщения определяются две-три координаты местоположения объекта и две-три составляющие вектора скорости его движения, а также осуществляется синхронизация шкал времени. Движение центра масс НКА описывается как решение задачи Коши для системы обыкновенных дифференциальных уравнений (ОДУ). Именно эта дифференциальная модель используется для прогнозирования по оперативной эфемеридной информации координат, скорости и ускорения НКА, а на этой основе прогнозируется местоположение объекта, его кинематические и динамические характеристики. В интерфейсном контрольном документе (ИКД) ГЛОНАСС в качестве примера численного метода, который может быть использован для интегрирования уравнений движения центра масс НКА, приводится метод Рунге – Кутты 4-го порядка [1]. Как показано в [2], повышение порядка разностного метода приводит к существенному росту времени расчета, что критично в рамках установленных границ времени расчета. Например, применение метода Рунге – Кутты – Фельберга 5-го порядка приводит к повышению времени расчета более чем на 50 %.

В излагаемой работе ставится вопрос о возможности снижения погрешности прогнозирования положения НКА при одновременном ускорении процесса вычислительной обработки с помощью численного моделирования на основе кусочно-интерполяционного интегрирования дифференциальных уравнений движения центра масс НКА. Помимо повышения точности приближения при условии не превышения границы времени расчета, в результате кусочно-интерполяционного решения задачи Коши для моделирующей дифференциальной системы должна достигаться непрерывность приближенного решения (приближения координат), а также непрерывность приближения производной от решения (составляющих вектора скорости центра масс НКА) на интервале прогнозирования. Ставится вопрос о хранении этих приближений в памяти компьютера.

Цель исследования – показать возможность снизить погрешность и сократить время расчета эфемерид НКА на основе численного моделирования движения спутника с помощью кусочно-интерполяционного решения системы ОДУ модели. Требуется также раскрыть значение хранимого непрерывного приближения решения задачи Коши для ОДУ и производной от него, полученных на основе кусочной интерполяции, применительно к постобработке результатов прогнозирования.

Исходный алгоритм расчета координат и составляющих вектора скорости центра масс НКА системы ГЛОНАСС по данным эфемерид. В ИКД ГЛОНАСС конструктивно описан алгоритм на основе приближенного решения задачи Коши для системы ОДУ, предназначенный для расчета координат и составляющих вектора скорости центра масс НКА на заданный момент времени ti шкалы московского декретного времени (МДВ) на 30-минутном интервале прогнозирования по данным эфемерид [1]. Пересчет эфемерид пользователем с момента tb шкалы МДВ на заданный момент времени ti той же шкалы, |ti – tb| ≤ 15 мин, проводится методом численного интегрирования системы ОДУ, описывающей движение центра масс НКА. В правых частях этих уравнений задаются функции ускорения, определяемые геоцентрической константой гравитационного поля Земли с учетом влияния атмосферы GM, зональным гармоническим коэффициентом второй степени J20, а также ускорениями от лунно-солнечных гравитационных возмущений. Эти уравнения движения определены в виде системы:

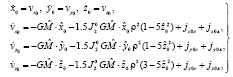, (1)

где 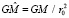; ; 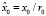; ; 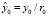; ; 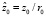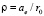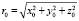jx0c, jy0c, jz0c, jx0л, jy0л, jz0л – ускорения от лунно-солнечных гравитационных возмущений; ae – большая полуось общеземного эллипсоида. Следующие исходные данные необходимы для пересчета эфемерид: N4 – номер эфемеридного четырехлетнего периода; NT – номер эфемеридных суток в эфемеридном четырехлетнем периоде; момент времени tb, координаты и составляющие вектора скорости центра масс НКА на момент времени tb из оперативной информации ГЛОНАСС; заданный момент времени ti шкалы МДВ, на который необходимо пересчитать координаты и составляющие вектора скорости НКА.

Дифференциальные уравнения (1) интегрируются в прямоугольной инерциальной геоцентрической системе координат 0X0Y0Z0. Ускорения от лунных и солнечных гравитационных возмущений вычисляются по формулам

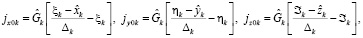(2)

где 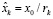; ; 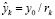; ; 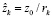; 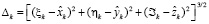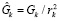k – индекс возмущающего тела; Gл, Gс – константы гравитационного поля Луны и Солнца; ξk, ηk, ℑk, rk – направляющие косинусы и удаление возмущающего тела, которые рассчитываются на каждый момент времени t из соотношений

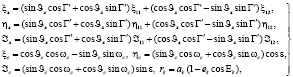, (3)

где 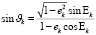; ; 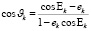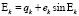– уравнение Кеплера для эксцентрической аномалии, которое решается методом итераций;

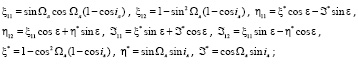
aл, aс – большие полуоси орбит Луны и Солнца; ел, ес – эксцентриситеты орбит Луны и Солнца; iл – среднее наклонение орбиты Луны к плоскости эклиптики.

Параметры нутации Луны и Солнца на момент времени t по шкале МДВ рассчитываются по формулам

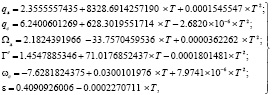, (4)

где 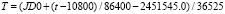, JD0 – текущая юлианская дата на 0 часов шкалы МДВ, которая до окончания 2119 г. рассчитывается по соотношению 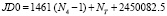[1].

Численное интегрирование уравнений движения НКА с применением кусочно-интерполяционного метода. Навигационное сообщение содержит информацию о параметрах движения НКА ГЛОНАСС. Эти данные записываются в формате RINEX [3] с 30-минутным интервалом в виде векторных составляющих положения, скорости и ускорения спутника. Ниже описывается численное моделирование движения отдельно взятого НКА ГЛОНАСС (в качестве примера исследуется движение НКА ГЛОНАСС № 730), которое выполняется на основе алгоритма (1)–(4). По результатам численных экспериментов сравнивается точность приближения, время расчета и качества полученных приближений в случаях использования разностных и кусочно-интерполяционных методов решения задачи (1)–(4).

Бортовые эфемериды НКА ГЛОНАСС № 730 в системе ПЗ-90.11 на момент времени 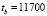шкалы МДВ даты 05.08.2021, пересчитанные в инерциальную геоцентрическую систему координат в соответствии с документацией из [1], представлены значениями [4]:

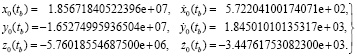. (5)

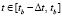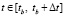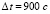Кусочно-интерполяционное приближение решения задачи (1)–(4) с начальными условиями (5) строится на интервалах ±15 мин относительно момента tb ( и , ). Значения лунно-солнечных ускорений рассчитываются по алгоритму (2)–(4) при каждом вызове функции правой части (1) в процессе численного моделирования.

Для сокращения времени решения без потери точности приближения ниже применяется модификация метода кусочно-интерполяционного решения задачи Коши для системы ОДУ. Модификация состоит в замене автоматического подбора параметров пользовательским подбором и фиксированием параметров метода. Исходный метод, обоснование, алгоритмизация и программная реализация представлены в [5, 6], необходимые для дальнейшего элементы метода поясняются непосредственно ниже.

Пусть требуется приближенно решить задачу Коши для системы

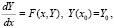(6)

где

,

,

.

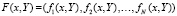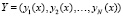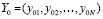Предполагается, что в области

,

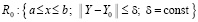здесь и ниже a = x0, 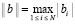, функция F(x,Y) определена, непрерывна, непрерывно дифференцируема и выполнены все условия существования и единственности решения. Пусть

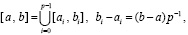
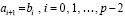, (7)

для предварительного описания абстрактно заданная функция f(x) определена на [a, b] из (7). На каждом подынтервале [ai, bi] строится интерполяционный полином Ньютона с равнооотстоящими узлами для интерполирования вперед:

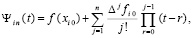
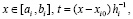
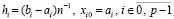. (8)

Полином (8) преобразуется к виду алгебраического полинома с числовыми коэффициентами

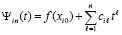, (9)

где , .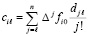

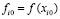Преобразование использует алгоритм восстановления коэффициентов полинома по его корням, отличный от формул Виета [5, 6]. Согласно этому алгоритму для данного частного случая (8) в 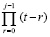следует положить 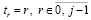, и значения коэффициентов восстанавливаются из соотношений

.

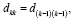
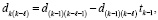
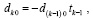
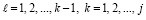Такое построение и преобразования выполняются для функции правой части (6), являющейся компонентом k-го уравнения системы, при каждом номере .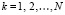

Соответственно полином и его коэффициенты в форме (8) и (9) отмечаются индексом k, преобразованная форма примет вид

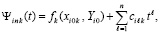
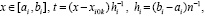
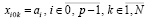. (10)

Здесь и ниже 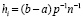. Выполняется интерполирование компонентов правой части (6). Для этого в fk(x,Y) подставляется приближенное значение 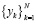, вначале 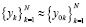. Функция fk(x,Y0) приближается полиномами (10) по изложенной схеме. При фиксированных значениях n и p из (7) на отрезке [ai, bi], сначала при i = 0, затем аналогично при 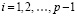выполняется итерационное уточнение, которое состоит в следующем.

Пусть согласно (10)

,

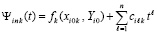тогда 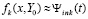, , 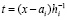hi – шаг интерполяции на [ai, bi].

Первообразная

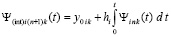, или

,

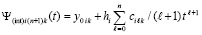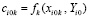
(на начальном подынтервале для значения произвольной постоянной полагается 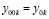, на последующих подынтервалах выбор 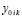поясняется ниже), принимается за приближение k-го компонента решения:

, .

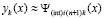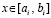Тогда

,

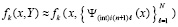и при том же значении n, на том же подынтервале строится интерполяционный полином вида (10) для аналогичного приближения:

,

.

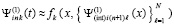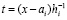От этого полинома снова берется первообразная с тем же значением константы

,

выполняется соответственная подстановка в правую часть,

,

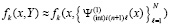которая затем аналогично интерполируется,

,

.

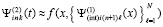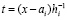Итерации

,

,

,

,

,

,

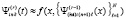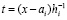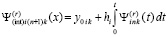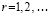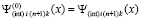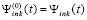продолжаются до априори заданной границы: 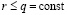. Выше неявно предполагалось, что за значение 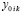было взято 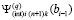. По окончании итераций на [ai, bi] выполняется переход к [ai+1, bi+1], где за значение 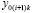принимается 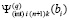. Отсюда

,

,

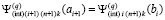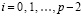и интегральные полиномы совпадают на каждой общей границе всех соседних подынтервалов. Таким образом, кусочно-интерполяционное приближение решения является непрерывной функцией 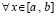. Кусочно-интерполяционное приближение производной от решения также, по построению, является непрерывной функцией на всем [a, b]. При этом имеет место равномерная сходимость 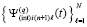к решению Y задачи (6) и равномерная сходимость 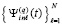к производной от решения Y’ [5, 6], если p→∞.

С некоторым отступлением от формализации выделяются следующие положения [5].

Предложение 1. Коэффициенты приближения производной от k-го компонента решения задачи (6), 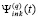, имеют, аналогично (9), (10), числовые значения

,

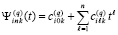по всем номерам подынтервалов из (7) они образуют массив из p строк вида

,

, … ,

.

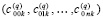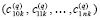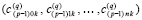Такой массив можно хранить в памяти компьютера в форме типизированного файла. Обращение к строке этого файла позволяет восстановить значение k-го компонента производной от решения по схеме Горнера. Номер строки типизированного файла, соответственной произвольному значению независимой переменной 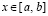, является номером подынтервала, которому принадлежит x, 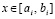, и определяется из соотношения:

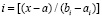, или,

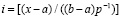, (11)

где [α] – целая часть числа α.

Предложение 2. Предложение 1 с точностью до обозначений повторяется для коэффициентов полинома 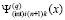, приближающего k-й компонент решения задачи (6). Они имеют числовые значения,

,

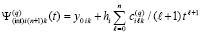по всем номерам подынтервалов из (7) образуют массив из p строк:

,

, … ,

,

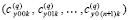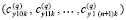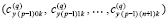который можно хранить в виде типизированного файла. Обращение к строке этого файла позволяет восстановить значение k-го компонента решения задачи (6) по схеме Горнера. Номер строки типизированного файла, соответственной произвольному значению независимой переменной 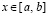, является номером подынтервала, которому принадлежит x, 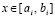, и определяется из соотношения (11).

Предложение 3. Предложения 1, 2 с точностью до обозначений сохраняются, если хранение коэффициентов полиномов в памяти компьютера выполняется не в форме типизированного файла, а в форме двумерного массива, номера строк которого соответствуют номерам подынтервалов из (7).

При использовании предложений 1–3 непрерывное приближение решения задачи (6) и непрерывное приближение его производной оказываются хранимыми и восстанавливаются в произвольной точке изменения независимой переменной по схеме Горнера вычисления значения полинома с оценкой времени 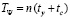, где ty – время бинарного умножения, tc – время бинарного сложения. При этом направление изменения независимой переменной может быть прямым, обратным и, вообще говоря, произвольным. Если требуется пересчитать значение решения или производной в любой точке отрезка приближения, то задачу (6) не требуется целиком решать заново – достаточно обратиться к соответственной строке типизированного файла или массива. Если пересчет требуется выполнить M раз, то рассматриваемая обработка (постобработка) выполнится в ≈M×τ раз быстрее (τ – время решения задачи (6)), чем с M-кратным использованием повторного численного интегрирования.

Ниже представлена программная реализация предложенного метода для решения задачи (1)–(5). С целью достижения минимальной временной сложности одновременно с максимальной точностью приближения в программе используется ряд упрощений, возможность которых определяется спецификой исходного алгоритма. Именно, выбраны следующие значения параметров: в (10) n = 8, граница числа итераций q = 12, число отрезков разбиения из (7) p = 1. Разбиение на подынтервалы (7) всегда дает положительный результат [5, 6]. Но высокое быстродействие с сохранением искомой точности в данном частном случае достигается при p = 1. Иными словами, метод программно реализован на одном подынтервале, совпадающем со всем отрезком приближения (интервалом прогнозирования).

Программная реализация (Delphi) выполняет расчет эфемерид НКА ГЛОНАСС в системе ПЗ-90.11 на заданный момент времени ti шкалы МДВ из 30-минутного интервала прогнозирования на основе кусочно-интерполяционного приближения решения задачи (1)–(5) с учетом общего случая, однако операторы для сохранения массива коэффициентов в типизированном файле закомментированы. Реализован только что отмеченный частный случай совпадения заданного интервала с единственным подынтервалом разбиения (7) при p = 1:

program fpi_glonass; {$APPTYPE CONSOLE} uses SysUtils, Math;

const Neq=6; {число уравнений в системе ОДУ (1)} N4=7; {номер эфемеридного четырехлетнего периода}

NT=583; {номер эфемеридных суток в эфемеридном четырехлетнем периоде}

tb=11700; {момент времени из оперативной информации ГЛОНАСС}

ti=12600; {заданный момент времени шкалы МДВ, на который необходимо пересчитать координаты и составляющие вектора скорости НКА}

type vectNeq = array[1..Neq] of extended; const y00:vectNeq = (24855158.20312, 345943.8476562, -5760185.546875,

-798.4914779663, -65.19222259521, -3447.617530823); {координаты и составляющие вектора скорости центра масс НКА на момент времени tb в системе ПЗ-90.11 из оперативной информации ГЛОНАСС}

procedure pi_calculation_of_ephemeris_glonass(N4,NT:integer; tb,ti:extended; y00:vectNeq);

const Npol=8;{степень n интерполяционных полиномов (10)} k_iter=12; {граница числа итераций q}

e_l=0.054900489; e_c=0.016719; i_l=0.0898041080; w3=7.2921151467e-5; J2=1082.62575e-6; a_c=1.49598e+11;

GM=3.986004418e+14; ae=6378136; G_l=4902.799e+9; G_c=13271244.0e+13; a_l=3.84385243e+8;

{FILEPATH=’D:\coeffs.bin’; type Arr_сoeff = array[0..29] of extended; var f_coeff: file of Arr_сoeff; dd: Arr_сoeff;}

type Prc=array[1..8] of extended; matr= array[0..Npol,0..Npol] of integer;

var y0,yn,yn0,yr: vectNeq; JD0,GMST,ERA,dT,S:extended; i:byte; vPrc:array[0..Npol] of Prc;

procedure ls_acceleration_prep(x:extended; var KEKr_:Prc); {расчет значений функций из (3)}

var sinv_l,cosv_l,sinv_c, cosv_c,w_c,eps,Gamma_,Ksi11,Ksi12,Eta11,Eta12, Kapa11, Kapa12:extended;

q_l,q_c, T, Omega_l, Ksi_, Eta_, Kapa_, El, Ec:extended;

function Ekk(q_k,e_k:extended):extended; var Ek_,Ek_new:extended; begin Ek_new:=q_k;

repeat Ek_:=Ek_new; Ek_new:=q_k+e_k*sin(Ek_); until abs(Ek_new-Ek_)<1e-15; Ekk:=Ek_; end;

begin T:=(JD0+(x-10800)/86400-2451545.0)/36525; q_l:=2.3555557435+8328.6914257190*T+0.0001545547*sqr(T);

q_c:=6.2400601269+628.3019551714*T-(2.6820e-6)*sqr(T);

Omega_l:=2.1824391966-33.7570459536*T+0.0000362262*sqr(T);

Gamma_:=1.4547885346+71.0176852437*T-0.0001801481*sqr(T);

w_c:=-7.6281824375+0.0300101976*T+(7.9741e-6)*sqr(T);

eps:=0.4090926006-0.0002270711*T; Ksi_:=1-sqr(cos(Omega_l))*(1-cos(i_l));

Eta_:=sin(Omega_l)*sin(i_l); Kapa_:=cos(Omega_l)*sin(i_l); Ksi11:=sin(Omega_l)*cos(Omega_l)*(1-cos(i_l));

Ksi12:=1-sqr(sin(Omega_l))*(1-cos(i_l)); Eta11:=Ksi_*cos(eps)-Kapa_*sin(eps);

Eta12:=Ksi11*cos(eps)+Eta_*sin(eps); Kapa11:=Ksi_*sin(eps)+Kapa_*cos(eps);

Kapa12:=Ksi11*sin(eps)-Eta_*cos(eps); El:=Ekk(q_l,e_l); Ec:=Ekk(q_c,e_c);

sinv_l:=(sqrt(1-sqr(e_l))*sin(El))/(1-e_l*cos(El)); sinv_c:=(sqrt(1-sqr(e_c))*sin(Ec))/(1-e_c*cos(Ec));

cosv_l:=(cos(El)-e_l)/(1-e_l*cos(El)); cosv_c:=(cos(Ec)-e_c)/(1-e_c*cos(Ec));

KEKr_[1]:=(sinv_l*cos(Gamma_)+cosv_l*sin(Gamma_))*Ksi11+(cosv_l*cos(Gamma_)-sinv_l*sin(Gamma_))*Ksi12;

KEKr_[2]:=(sinv_l*cos(Gamma_)+cosv_l*sin(Gamma_))*Eta11+(cosv_l*cos(Gamma_)-sinv_l*sin(Gamma_))*Eta12;

KEKr_[3]:=(sinv_l*cos(Gamma_)+cosv_l*sin(Gamma_))*Kapa11+(cosv_l*cos(Gamma_)-sinv_l*sin(Gamma_))*Kapa12; KEKr_[7]:=a_l*(1-e_l*cos(El)); KEKr_[4]:=cosv_c*cos(w_c)-sinv_c*sin(w_c);

KEKr_[5]:=(sinv_c*cos(w_c)+cosv_c*sin(w_c))*cos(eps); KEKr_[6]:=(sinv_c*cos(w_c)+cosv_c*sin(w_c))*sin(eps);

KEKr_[8]:=a_c*(1-e_c*cos(Ec)); end;

{подпрограмма-функция вычисления значений компонентов вектор-функции правой части (1)}

function f(eq:integer;x:extended;yy:vectNeq;KEKr:Prc):extended;

var r,GM_,y1_,y2_,y3_,ro,jx0_c,jy0_c,jz0_c,jx0_l,jy0_l,jz0_l:extended;

procedure ls_acceleration(y1,y2,y3:extended;KEKr:Prc; var jx0_c,jy0_c,jz0_c, jx0_l, jy0_l,jz0_l:extended);

var delta_c,delta_l,x_c,y_c,z_c,x_l,y_l,z_l,Gl_,Gc_:extended;

begin x_l:=y1/KEKr[7]; y_l:=y2/KEKr[7]; z_l:=y3/KEKr[7]; Gl_:=G_l/sqr(KEKr[7]);

x_c:=y1/KEKr[8]; y_c:=y2/KEKr[8]; z_c:=y3/KEKr[8]; Gc_:=G_c/sqr(KEKr[8]);

delta_l:=Power(sqr(KEKr[1]-x_l)+sqr(KEKr[2]-y_l)+sqr(KEKr[3]-z_l),1.5);

delta_c:=Power(sqr(KEKr[4]-x_c)+sqr(KEKr[5]-y_c)+sqr(KEKr[6]-z_c),1.5);

jx0_l:=Gl_*((KEKr[1]-x_l)/delta_l-KEKr[1]); jy0_l:=Gl_*((KEKr[2]-y_l)/delta_l-KEKr[2]);

jz0_l:=Gl_*((KEKr[3]-z_l)/delta_l-KEKr[3]); jx0_c:=Gc_*((KEKr[4]-x_c)/delta_c-KEKr[4]);

jy0_c:=Gc_*((KEKr[5]-y_c)/delta_c-KEKr[5]); jz0_c:=Gc_*((KEKr[6]-z_c)/delta_c-KEKr[6]);end;

begin case eq of 1: f:=yy[4]; 2: f:=yy[5]; 3: f:=yy[6]; else begin r:=sqrt(yy[1]*yy[1]+yy[2]*yy[2]+yy[3]*yy[3]);

GM_:=GM/sqr(r); y1_:=yy[1]/r; y2_:=yy[2]/r; y3_:=yy[3]/r; ro:=ae/r;

ls_acceleration(yy[1],yy[2],yy[3],KEKr,jx0_c,jy0_c,jz0_c,jx0_l,jy0_l,jz0_l);

case eq of 4: f:=-GM_*y1_-1.5*J2*GM_*ro*ro*y1_*(1-5*sqr(y3_))+jx0_c+jx0_l;

5: f:=-GM_*y2_-1.5*J2*GM_*ro*ro*y2_*(1-5*sqr(y3_))+jy0_c+jy0_l;

6: f:=-GM_*y3_-1.5*J2*GM_*ro*ro*y3_*(3-5*sqr(y3_))+jz0_c+jz0_l; end; end; end; end;

{кусочно-интерполяционное приближение решения задачи Коши (1) – (5)}

procedure RD(print:boolean;yin:vectNeq; A_nach,B_konech:extended; var yout:vectNeq);

const dp: array[1..8,1..8] of extended =((1,-1/2,2/6,-6/24,24/120,-120/720,720/5040,-5040/40320),

(0,1/2,-3/6,11/24,-50/120,274/720,-1764/5040,13068/40320),(0,0,1/6,-6/24,35/120,-225/720,

1624/5040,-13132/40320),(0,0,0,1/24,-10/120,85/720,-735/5040,6769/40320),

(0,0,0,0,1/120,-15/720,175/5040,-1960/40320),(0,0,0,0,0,1/720,-21/5040,322/40320),

(0,0,0,0,0,0,1/5040,-28/40320),(0,0,0,0,0,0,0,1/40320));

type Mmatr=array[0..Npol,0..Npol] of vectNeq; vect=array[0..Npol] of extended; Mvect= array[0..Npol] of vectNeq;

var i,k,j,iter,r:byte; h:extended; x:vect; pp,s:vectNeq; y,fy,A:Mvect; dy:Mmatr;

begin h:=(B_konech-A_nach)/Npol;

for j:=0 to Npol do begin x[j]:=A_nach+j*h; ls_acceleration_prep(x[j],vPrc[j]);end;

for j:=0 to Npol do for i:=1 to Neq do y[j,i]:=yin[i];

for i:=1 to Neq do begin fy[0,i]:=f(i,x[0],y[0],vPrc[0]); A[0,i]:=fy[0,i]; end;

for iter:=1 to k_iter do begin for j:=1 to Npol do for i:=1 to Neq do fy[j,i]:=f(i,x[j],y[j],vPrc[j]);

for j:=0 to Npol-1 do for i:=1 to Neq do dy[1,j,i]:=fy[j+1,i]-fy[j,i];

for k:=2 to Npol do for j:=0 to Npol-k do for i:=1 to Neq do dy[k,j,i]:=dy[k-1,j+1,i]-dy[k-1,j,i];

for k:=1 to Npol do begin for i:=1 to Neq do s[i]:=0; for j:=k to Npol do

for i:=1 to Neq do s[i]:=s[i]+dp[k,j]*dy[j,0,i];for i:=1 to Neq do A[k,i]:=s[i]; end;

for j:=1 to Npol do begin for i:=1 to Neq do pp[i]:=A[Npol,i]/(Npol+1);

for r:=Npol-1 downto 0 do for i:=1 to Neq do pp[i]:=pp[i]*j+A[r,i]/(r+1);

for i:=1 to Neq do y[j,i]:=pp[i]*h*j+y[0,i]; end; end;

{сохранение массива коэффициентов полиномов, аппроксимирующих координаты центра масс НКА на интервале прогнозирования, в типизированный файл (массив состоит из одной строки с коэффициентами полиномиальных приближений компонентов решения системы, соответствующих координатам x, y и z)}

{if print then begin AssignFile(f_coeff,FILEPATH); rewrite(f_coeff); for i:=1 to 3 do dd[(Npol+2)*(i-1)]:=y[0,i];

for k:=1 to Npol+1 do for i:=1 to 3 do dd[k+(Npol+2)*(i-1)]:=A[k-1,i]*h/k; write(f_coeff,dd); Close(f_coeff); end;}

for i:=1 to Neq do yout[i]:=y[Npol,i]; end;

begin JD0:=1461*(N4-1)+NT+2450082.5; dT:=(JD0-2451545.0)/36525;

ERA:=2*PI*(0.7790572732640+1.00273781191135448*(JD0-2451545.0));

GMST:=ERA+7.03270726e-8+0.0223603658710194*dT+6.7465784654e-6*power(dT,2)

-2.1332e-12*power(dT,3)-1.452308e-10*power(dT,4)-1.784e-13*power(dT,5);

{расчет начальных условий для интегрирования системы (1) путем пересчета координат и составляющих вектора скорости центра масс НКА в геоцентрическую систему координат} S:=GMST+w3*(tb-10800); y0[1]:=y00[1]*cos(S)-y00[2]*sin(S); y0[2]:=y00[1]*sin(S)+y00[2]*cos(S); y0[3]:=y00[3];

y0[4]:=y00[4]*cos(S)-y00[5]*sin(S)-w3*y0[2]; y0[5]:=y00[4]*sin(S)+y00[5]*cos(S)+w3*y0[1]; y0[6]:=y00[6];

RD(True,y0,tb,ti,yn0); {кусочно-интерполяционное приближение решения задачи Коши}

{пересчет результатов приближения координат и составляющих вектора скорости центра масс НКА в момент времени ti в систему координат ПЗ-90.11} S:=GMST+w3*(ti-10800);

yn[1]:=yn0[1]*cos(S)+yn0[2]*sin(S); yn[2]:=-yn0[1]*sin(S)+yn0[2]*cos(S); yn[3]:=yn0[3];

yn[4]:=yn0[4]*cos(S)+yn0[5]*sin(S)+w3*yn[2]; yn[5]:=-yn0[4]*sin(S)+yn0[5]*cos(S)-w3*yn[1]; yn[6]:=yn0[6];

writeln(ti); writeln(‘ x=’,yn[1],’ y=’,yn[2],’ z=’,yn[3]); writeln(‘vx=’,yn[4],’ vy=’,yn[5],’ vz=’,yn[6]);

RD(False,yn0,ti,tb,yr); {расчет погрешности приближения путем обратного интегрирования задачи Коши}

writeln; for i:=1 to Neq do write(‘Pogr’,i,’ =’,Format(‘ %1.4e’,[abs(yr[i]-y0[i])]),’; ‘); end;

begin pi_calculation_of_ephemeris_glonass(N4,NT,tb,ti,y00); readln; end.

Результат работы программы:

ti= 1.26000000000000E+0004

x= 2.39489258119706E+0007 y= 3.40159756877465E+0005 z=-8.79710015725756E+0006

vx=-1.21004870882318E+0003 vy= 6.13653373754929E+0001 vz=-3.29014462102794E+0003

P1= 0.000E+000; P2= 0.000E+000; P3= 0.000E+000; P4= 0.000E+000; P5= 0.000E+000; P6= 0.000E+000;

Пересчет эфемерид выполнен на момент времени ti = 12600. Погрешность приближения оценивалась по методике [7] – путем обратного интегрирования задачи (1)–(5) на отрезке [ti, tb] (при ti < tb на отрезке [tb, ti]) с начальными данными, полученными при решении прямой задачи в момент времени ti. Для кусочно-интерполяционного приближения получены «нулевые» в формате вывода данных extended значения абсолютной погрешности приближения компонентов решения системы. Иными словами, погрешность кусочно-интерполяционного решения задачи (1)–(5) совпала с погрешностью представления начальных данных (5), при этом время решения составило 0.140 мс. Здесь и ниже погрешность приближения координат НКА указана в метрах, составляющих вектора скорости центра масс НКА – в метрах в секунду, значение времени решения – в миллисекундах. Время решения по аналогии с [2] рассчитывается как среднее арифметическое для 100000 последовательных решений на компьютере с процессором 11th GenIntel(R) Core(TM) i7-1165G7.

Таблица 1

Погрешность и время расчета эфемерид НКА посредством решения задачи (1)–(5)

Приближение решения этой же задачи с помощью метода Рунге – Кутты 4-го порядка с шагом интегрирования h = 1c также характеризуется «нулевыми» значениями погрешности вследствие ограниченной точности начальных данных (5). Однако время решения существенно больше: 29.929 мс (шаг интегрирования h = 1c выбран с целью сравнения времени расчета при условии достижения высокой точности приближения – в практических расчетах рекомендуется применять метод Рунге – Кутты 4-го порядка с шагом h = 60c [1, 2]). В табл. 1 представлены результаты численных экспериментов по расчету эфемерид НКА ГЛОНАСС № 730 на основе приближенного решения задачи (1)–(5) на отрезках 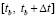, , 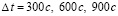с помощью метода Рунге – Кутты 4-го порядка. В табл. 1 величина шага интегрирования h = 1c, как только что отмечено, специально взята меньше рекомендуемого в [1, 2] шага h = 60c. Кусочно-интерполяционный метод, как отмечалось, взят с параметрами n = 8, q = 12. В таблице принята норма 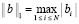для вектора абсолютной погрешности приближения компонентов системы (1).

Согласно табл. 1 применение предложенного метода позволяет на два десятичных порядка ускорить существующий [1, 2] процесс расчета координат и составляющих вектора скорости центра масс НКА при достижении превышения требуемой точности приближения.

Если согласно рекомендации [1, 2] для снижения трудоемкости применить метод Рунге – Кутты 4-го порядка с шагом 60 c, то для рассматриваемой задачи расчет эфемерид НКА ГЛОНАСС № 730 на момент времени ti = 12600 выполнится со следующими значениями абсолютной погрешности:

P1=3.959E-005; P2=1.003E-004; P3=1.925E-004; P4=3.704E-008; P5=1.367E-009; P6=6.953E-009;

при этом время решения составит 0.522 мс. Расчет с применением кусочно-интерполяционного метода выполняется в ≈4 раза быстрее, причем без накопления погрешности. Здесь и ниже погрешность приближения рассчитывается на основе сравнения с эталонным приближением эфемерид НКА, выполненным с применением кусочно-интерполяционного метода с параметрами n = 8, q = 12 (аналогичная погрешность получилась бы при сравнении с эталоном, рассчитанным по методу Рунге – Кутты 4-го порядка при h = 1c).

Замечание 1. Следует отметить особенность применения предложенного метода для решения задачи (1)–(5), которая учитывается в представленной программе fpi_glonass для снижения времени расчета. При кусочно-интерполяционном приближении решения рассматриваемой задачи большая часть числа обращений к функциям правой части (1) производится в процессе выполнения итераций. При этом моменты времени, определяемые в качестве узлов интерполяции, остаются неизменными в процессе итераций. В (1) многие параметры, включая направляющие косинусы и удаление возмущающего тела (3), зависят только от времени Т в юлианских столетиях по 36525 эфемеридных суток от эпохи 2000 года, 1 января, 12 ч (UTC(SU)) до момента времени t. Поэтому значения таких параметров расчитываются до начала итерационного уточнения. Это снижает время построения требуемых приближений эфемерид. Такой подход к снижению времени расчета на основе метода Рунге – Кутты неприменим вследствие обращения к функции правой части на каждом шаге метода.

Время повторного расчета (в случае его необходимости) эфемерид НКА для произвольного момента времени из интервала прогнозирования 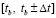, , 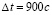можно существенно снизить посредством представленной в предложениях 1–3 возможности хранения коэффициентов непрерывного кусочно-интерполяционного приближения решения задачи (1)–(5). После однократного построения приближения в последующем оно восстанавливается как значение полинома с хранимыми коэффициентами, вычисляемое по схеме Горнера.

Для формирования типизированного файла с коэффициентами полиномов, аппроксимирующих координаты центра масс НКА на интервале прогнозирования, в программе fpi_glonass нужно раскомментировать соответствующие блоки операторов. Далее, восстановление значений эфемерид НКА для произвольного момента времени из интервала прогнозирования и их пересчет из инерциальной геоцентрической системы координат в систему ПЗ-90.11 в соответствии с документацией из [1] выполняется представленной ниже программой:

program calc_fpi; {$APPTYPE CONSOLE} uses SysUtils, Math;

const N4=7; {номер эфемеридного четырехлетнего периода}

NT=583; {номер эфемеридных суток в эфемеридном четырехлетнем периоде}

tb=11700; ti=12600; {границы интервала прогнозирования эфемерид НКА}

tpr=12600; {момент времени из интервала прогнозирования}

FILEPATH=’D:\coeffs.bin’; n=9; h=112.5; {файл с коэффициентами полиномов, аппроксимирующих координаты центра масс НКА и параметры приближения}

type Arr_coeff=array[0..29] of extended; var f_coeff:file of Arr_coeff;dd:Arr_coeff; const w3=7.2921151467e-5;

type vectNeq = array[1..6] of extended; var i:integer; yn0,yn:vectNeq; JD0,ERA,GMST,dT,S:extended;

function calc(num:byte;tpr:extended):extended; type Coeff=array[0..n] of extended; var d:Coeff; j:integer; t:extended;

function gorner(const d:Coeff): extended; var pp:extended; i:integer;

begin pp:=d[n]; for i:=1 to n do pp:=pp*t+d[n-i]; gorner:=pp; end;

function gorner_pr (const d:Coeff): extended; var pp:extended; i:integer;

begin pp:=d[n]*n/h; for i:=1 to n-1 do pp:=pp*t+d[n-i]*(n-i)/h; gorner_pr:=pp; end;

begin t:=(tpr-tb)/h; case num of 1,2,3: begin for j:=0 to n do d[j]:=dd[j+(n+1)*(num-1)]; calc:=gorner(d); end;

4,5,6: begin for j:=0 to n do d[j]:=dd[j+(n+1)*(num-3-1)]; calc:=gorner_pr(d); end; end; end;

begin JD0:=1461*(N4-1)+NT+2450082.5; dT:=(JD0-2451545.0)/36525;

ERA:=2*PI*(0.7790572732640+1.00273781191135448*(JD0-2451545.0));

GMST:=ERA+7.03270726e-8+0.0223603658710194*dT+6.7465784654e-6*power(dT,2)

-2.1332e-12*power(dT,3)-1.452308e-10*power(dT,4)-1.784e-13*power(dT,5);

AssignFile(f_coeff, FILEPATH); Reset(f_coeff); read(f_coeff,dd);

for i := 1 to 6 do yn0[i]:=calc(i,tpr);

S:=GMST+w3*(tpr-10800); yn[1]:=yn0[1]*cos(S)+yn0[2]*sin(S);

yn[2]:=-yn0[1]*sin(S)+yn0[2]*cos(S);yn[3]:=yn0[3];

yn[4]:=yn0[4]*cos(S)+yn0[5]*sin(S)+w3*yn[2];

yn[5]:=-yn0[4]*sin(S)+yn0[5]*cos(S)-w3*yn[1]; yn[6]:=yn0[6]; CloseFile(f_Coeff);

writeln(‘tpr=’,tpr); writeln(‘ x=’,yn[1],’ y=’,yn[2],’ z=’,yn[3]); writeln(‘vx=’,yn[4],’ vy=’,yn[5],’ vz=’,yn[6]); readln;

end.

Результат работы программы:

tpr=12600

x=2.39489258119706E+0007 y=3.40159756877465E+0005 z=-8.79710015725756E+0006

vx=-1.21004870882318E+0003 vy=6.13653373754929E+0001 vz=-3.29014462102794E+0003

Таблица 2

Погрешность и время повторного расчета эфемерид НКА с учетом хранимости коэффициентов кусочной интерполяции

Метод позволяет хранить лишь коэффициенты полиномов, аппроксимирующих координаты центра масс НКА: значения составляющих вектора скорости восстанавливаются без потери точности как значения производных от полиномов, аппроксимирующих координаты центра масс (процедура gorner_pr).

В табл. 2 представлены результаты численных экспериментов по расчету эфемерид НКА ГЛОНАСС № 730 на основе численного решения задачи (1)–(5) с помощью метода Рунге – Кутты 4-го порядка с шагом 60 c и на основе восстановления кусочно-интерполяционного приближения решения этой задачи из типизированного файла.

Согласно табл. 2 применение хранимого кусочно-интерполяционного приближения решения задачи (1)–(5) на интервале прогнозирования снижает время восстановления решения примерно в 7 раз для Δt = 5 мин, в 12 раз для Δt = 10 мин, в 20 раз для Δt = 15 мин. При этом точность восстановленного приближения существенно превышает допустимое значение.

Замечание 2. При расчете эфемерид НКА ГЛОНАСС на основе восстановления кусочно-интерполяционного приближения решения задачи Коши из типизированного файла основной составляющей времени расчета (табл. 2) является время открытия и закрытия типизированного файла.

Замечание 3. Без учета времени открытия и закрытия типизированного файла расчет эфемерид НКА ГЛОНАСС для произвольного момента времени из интервала прогнозирования занимает время 0.0007 мс.

Замечание 4. Нетрудно видеть, что разбиение интервала ±15 мин относительно момента tb ( t ∈ [tb– Δt, tb] и t ∈ [tb, tb + Δt], Δt = 900 c) на сравнительно малое число подынтервалов в соответствии с (7) позволяет добиться аналогично высокой точности приближения с помощью полиномов степени n = 4. В этом случае указанное в замечании 3 время восстановления решения задачи (1)–(5) сократится примерно вдвое.

Рассматриваемое в замечании 4 разбиение потребуется при применении метода для решения задачи Коши для системы ОДУ на интервале существенно большей длины. В [6] показано, что применение кусочно-интерполяционного метода характеризуется высокой точностью приближенного решения на отрезке произвольно фиксированной длины при наименьшей временной сложности, причем инвариантно относительно вида задачи. При изменении рекомендованного в [1] алгоритма расчета интервал требуемого высокоточного прогноза эфемерид НКА ГЛОНАСС может быть увеличен. В частности, в [8] предлагается новый алгоритм высокоточного прогноза эфемерид НКА ГЛОНАСС (с учетом дополнительных факторов, влияющих на орбиты спутников), который позволяет в ~ 3 раза повысить точность прогнозируемых эфемерид спутников этой системы и увеличить «время жизни» эфемерид ГЛОНАСС с 0,5 ч до суток.

Согласно изложенному с помощью кусочно-интерполяционного интегрирования уравнений движения центра масс НКА достигается снижение погрешности прогнозирования положения НКА при одновременном ускорении вычислительной обработки. Кроме того, в результате кусочно-интерполяционного решения задачи (1)–(5) достигается непрерывность приближения координат, а также составляющих вектора скорости центра масс НКА на интервале прогнозирования. Эти приближения могут быть хранимыми для всего интервала прогнозирования в виде типизированных файлов, что позволяет выполнять пересчет положения НКА в любых точках интервала без повторного решения задачи (1)–(5).

Об особенностях предложенного численного моделирования движения НКА. Время расчета эфемерид НКА кусочно-интерполяционным методом является минимальным, фиксированным и не зависит от момента времени ti, |ti – tb| ≤ 15 мин, (табл. 1, 2). На основе кусочно-интерполяционного приближения помимо значений координат и составляющих вектора скорости центра масс НКА в требуемый момент времени ti можно выполнить расчет ускорений. Предложенное приближенное решение задачи (1)–(5) непрерывно и непрерывно дифференцируемо на интервале прогнозирования. Дополнительное ускорение численного моделирования возможно за счет применения кусочной интерполяции суперпозиций функций в правой части (1) с помощью интерполяционных полиномов Лагранжа или Ньютона, преобразованных, аналогично (10), к виду алгебраических полиномов с числовыми коэффициентами [9]. Такой метод инвариантен относительно вида функции и диапазона независимой переменной, характеризуется высокой точностью приближения и одновременно малой временной сложностью. Для класса повторяющихся функций временная сложность сконструированного в [9] алгоритма измеряется степенью полинома, – n(ty + tc), где ty, tc – время бинарного умножения и сложения. С применением этого алгоритма можно построить кусочно-интерполяционные приближения функций ξл, ηл, ℑл, rл / ал, ξc, ηc, ℑс, rc / аc, которые расчитываются из (3) для определения ускорения от лунно-солнечных гравитационных возмущений. Рассматриваемые функции зависят только от времени T в юлианских столетиях от эпохи 2000 г. до требуемого момента времени t. При этом для численного моделирования движения НКА системы ГЛОНАСС вплоть до 2047 г. диапазон значений T не выходит из отрезка [0, 0.5]. Коэффициенты полиномов кусочно-интерполяционного приближения ξл, ηл, ℑл, rл / ал, ξc, ηc, ℑс, rc / аc, можно вычислить априори для T ∈ [0, 0.5] и хранить их массив в памяти компьютера. С применением адресации (11) это влечет существенное сокращение времени вычисления ускорений от лунных и солнечных гравитационных возмущений. Согласно проведенному численному эксперименту рассматриваемые функции могут быть приближены полиномами шестой степени с границей абсолютной погрешности порядка 10–15 (при разбиении отрезка приближения на 216 подынтервалов). В результате значения направляющих косинусов и удалений Луны и Солнца, необходимые для определения ускорений от лунно-солнечных гравитационных возмущений из (2), могут быть вычислены на отрезке T ∈ [0, 0.5] с точностью порядка 10–15 за время 6(ty + tc).

Возможность использования хранимых коэффициентов кусочной интерполяции суперпозиций функций в правой части (1) с целью снижения времени расчета ускорений от лунно-солнечных гравитационных возмущений в программе fpi_glonass не реализована вследствие причин, указанных в замечании 1. В случае если бы задача (1)–(5) решалась разностным методом, восстановление значений функций (3) на основе хранимых коэффициентов аппроксимирующих полиномов существенно снизило бы время расчета таким методом.

Об архивации непрерывных приближений и прогнозировании отрезка траектории движения объекта. Целесообразно пояснить значение предложенной разновидности кусочной интерполяции решения задачи (1)–(5) для архивации прогнозирования. Поскольку отрезок 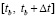(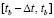), 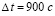остается постоянным для численного решения этой задачи, то при любом выборе разбиения (7) для 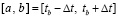двумерный массив коэффициентов рассматриваемой кусочной интерполяции будет постоянным на всем этом отрезке. Необходима оговорка, что речь идет о решении задачи Коши с фиксированными начальными значениями на 30-минутном интервале прогнозирования. При изменении начальных значений соответственно изменится массив коэффициентов. При фиксированных начальных значениях задачи (1)–(5) приближенное решение со всеми отмеченными качествами с единственностью будет представлено одним и только одним двумерным массивом коэффицентов, сформированным в процессе прогнозирования путем численного моделирования. Такой массив естественно хранить в виде типизированного файла. С учетом того, что каждый компонент решения (и его первых двух производных) восстанавливается по строке коэффициентов, соответствующей номеру подынтервала, с применением адресации (11) для произвольной точки 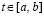, получается удобный вид хранения всего процесса прогнозирования на данном отрезке. При этом аналитические качества восстановленного приближения сохраняются и практически дают всю информацию о поведении решения (о поведении центра масс НКА) в любой момент времени на данном интервале прогнозирования. Так, для представленного в программах fpi_glonass и calc_fpi примера рассматриваемый массив состоит всего из одной строки, которая содержит набор из 10 коэффициентов для каждого интерполируемого компонента решения задачи (1)–(5). И именно такой массив (типизированный файл) включает всю требуемую информацию для последующей обработки архива. Для нескольких соседних интервалов прогнозирования понадобится число хранимых файлов, равное числу интервалов, однако их можно объединить в один файл с сохранением его структуры: начальные данные для каждого интервала изменят значение коэффициентов, но не повлияют на их взаимное расположение и на способ их считывания.

Представляется важным следующее. Поскольку предложенный метод примерно в 4 раза ускоряет процесс расчета координат и составляющих вектора скорости центра масс НКА, причем он дает точность приближения, достигаемую методом Рунге – Кутты только с шагом 1c (в 60 раз меньше рекомендованного шага) на отдельном интервале прогнозирования (табл. 1), то с требуемым ограничением по времени он может пройти 4 таких интервала при фиксированных начальных значениях. Иными словами, кусочно-интерполяционный метод, не нарушая временных ограничений, может приближенно решить задачу (1)–(5) с одними и теми же начальными значениями, поступившими из первого (по числу интервалов) навигационного сообщения, на отрезке из четырех последовательных интервалов прогнозирования. С учетом экспериментально подтвержденной высокой точности метод не выйдет из допустимых пределов накопления погрешности в границах четырех рассматриваемых интервалов прогнозирования. Если при этом выполняется запоминание коэффициентов интерполирующих полиномов в структуре типизированного файла, то получатся не только требуемые выходные данные для каждого интервала прогнозирования, но и могут быть восстановлены из файла, практически без потери времени, данные для прогноза в любой точке каждого из рассматриваемых интервалов. Восстановление возможно также на произвольном множестве точек из таких интервалов или во всей их естетвенной последовательности. Последовательное восстановление требуемых значений в каждой точке каждого интервала восстанавливает весь отрезок линии движения НКА на данном множестве интервалов прогнозирования (учитывается непрерывность кусочно-интерполяционного приближения). Восстановление можно выполнять не как отдельную операцию после прохождения всех рассматриваемых интервалов, а после прохождения каждого интервала в отдельности по ходу решения задачи (1)–(5) для последовательности всех интервалов. Отсюда возникают предпосылки прогнозирования в заданное время не только одной точки местоположения НКА (объекта), но возможно прогнозировать полный отрезок траектории движения объекта, причем не только на одном интервале, но на всем их рассматривамом множестве. Вместе с прогнозированием отрезка траектории НКА (объекта) предсказывается скорость движения (производная интерполирующего полинома), а также ускорение (его вторая производная).

Нетрудно видеть, что смена начальных значений на каждом интервале прогнозирования ничего не меняет в данных рассуждениях, за исключением времени прогноза (новые начальные значения на каждый интервал в ранее изложенной версии следует ожидать). Но, во-первых, в силу точности приближения они могут не потребоваться до окончания отрезка из четырех интервалов прогнозирования. Во-вторых, к новым начальным значениям, в последовательности их поступления, можно возвращаться по окончании прохождения четырех интервалов с целью корректировать уже полученный полный прогноз. Как вариант, это можно делать после прохождения каждого из интервалов, сверяя отклонение новых начальных значений от результата решения в конце интервала. Сверка определит необходимость решения с новыми начальными значениями или отсутствие такой необходимости. Сверку решения можно выполнять и с архивными значениями, априори сохраняемыми для четырех интервалов. Конвейер из четырех процессоров может выполнять прогноз имманентно (с поинтервальной коррекцией прогноза и архивацией) на произвольно заданном отрезке времени. Наиболее вероятно, что комбинирование границы погрешности кусочно-интерполяционного приближения со временем прохождения интервала прогнозирования даст возможность рассматривать удлинение 30-минутного интервала прогнозирования не в 4, а в гораздо большее число раз. При этом прогнозироваться будет не точка положения НКА (объекта), а отрезок траектории, по которой он движется, на все время объединения интервалов прогнозирования.

Предлагаемый способ архивации позволит повысить эффективность и точность решения пользователями координатно-временных задач в апостериорном режиме моделирования движения НКА при его использовании в Системе высокоточного определения эфемерид и временных поправок (СВОЭВП) ГЛОНАСС по сравнению с традиционным применением апостериорной высокоточной эфемеридно-временной информации в дискретных узловых точках [10]. В [10] рекомендуется выполнять расчет движения центра масс НКА на любой заданный момент времени по рассчитанным СВОЭВП узловым точкам с использованием интерполяционного полинома, а расчет текущей скорости движения НКА путем дифференцирования такого полинома. Это влечет накопление погрешности интерполяции и дифференцирования, что исключается в случае применения предложенного способа архивации. Передача потребителям СВОЭВП вместо узловых точек со значениями эфемерид НКА массива с коэффициентами непрерывного кусочно-полиномиального приближения траектории (и скорости), которое хранит высокоточные значения приближенного решения в каждой точке интервала прогнозирования, поэтому не требует интерполяции и какой-либо дополнительной вычислительной обработки, позволит существенно ускорить и повысить точность потребительского расчета рассматриваемых эфемерид.

Содержание предложенного подхода соотносится с тем, что аналогичный подход с целью высокоточной быстродействующей обработки применяется в программе ORBGEN, входящей в состав Bernese GNSS (высокоточного программного обеспечения для постобработки наблюдений глобальных навигационных спутниковых систем, разработанного в астрономическом институте Бернского университета) [11]. Приближенное решение уравнений движения НКА строится в виде полинома, приближение сохраняется в форме файла с коэффициентами аппроксимирующих полиномов. Постобработка выполняется на основе метода коллокации (разновидность неявного метода Рунге – Кутты), что, в отличие от предложенного подхода, ограничивает снижение погрешности и временной сложности.

Заключение

Численное моделирование движения НКА системы ГЛОНАСС по данным эфемерид выполнено с применением кусочно-интерполяционного решения задачи Коши для системы ОДУ, описывающей движение центра масс. Как результат достигается сравнительно высокая точность, непрерывность приближенного решения и его производной, что позволяет получить координаты НКА с превышением требуемой точности в произвольно заданные моменты времени с малой временной сложностью. Процесс расчета реализован в виде процедуры с параметрами, определяемыми из навигационного сообщения, может быть автоматизирован с повышением быстродействия. Дополнительное ускорение численного моделирования движения НКА, а также ускорение постобработки архива прогнозирования возможно с использованием хранимых коэффициентов непрерывных полиномиальных приближений компонентов решения ОДУ.

Библиографическая ссылка