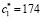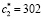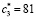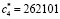Построение современного общества невозможно представить без использования информационных технологий (ИТ). Особое место среди ИТ занимает информационно-коммуникационная сеть Интернет. Поэтому в настоящее время государством решается проблема предоставление ресурсов интернета всем гражданам нашей страны. Решить данную проблему возможно за счет создания низкоорбитальных систем спутникового интернета (НССИ). В настоящее время функционирует такая система – StarLink, группировка которой содержит более 2000 спутников [1, 2]. Для обеспечения широкополосного доступа в интернет в беспроводных системах широко используется технология OFDM. Основные достоинства данной технологии определяются благодаря алгоритмам быстрого преобразования Фурье (БПФ) и обратного БПФ [3]. Для повышения спектральной эффективности систем OFDM в работах [4, 5] предлагается вместо БПФ использовать дискретные вейвлет-преобразования (ДВП). Однако коэффициенты ДВП представляют собой иррациональные числа, что приводит к накоплению ошибок округления. Устранить данные недостатки можно за счет использования целочисленных дискретных вейвлет-преобразований (ЦДВП), реализуемых в полях Галуа. При этом применение табличной реализации арифметических операций в ЦДВП позволит повысить скорость ортогональных преобразований сигналов в системах, использующих технологию OFDM. Поэтому создание математических моделей ЦДВП Добеши в полях Галуа, использование которых позволит снизить временные затраты на цифровую обработку сигналов и увеличить скорость передачи информации в системах НССИ, можно отнести к актуальным задачам.
Использование БПФ и ОБПФ позволяет увеличить спектральную эффективность беспроводных систем OFDM. Однако данные ортогональные преобразования сигналов имеют относительно большой уровень боковых лепестков спектра OFDM сигнала. Замена процедур БПФ и ОБПФ на целочисленные дискретные вейвлет-преобразования (ЦДВП), выполняемые в поле Галуа, позволит уменьшить уровень боковых лепестков, а также повысить скорость обработки сигналов за счет использования LUT-таблиц при вычислениях. Цель статьи – увеличение скорости цифровой обработки сигналов в системах OFDM за счет применения разработанных матмоделей ЦДВП, которые реализуются в полях Галуа.
Материалы и методы исследования
Предложение о замене ортогональных преобразований сигналов в системах OFDM основано на том, что вейвлет-преобразования (ВП) исходного сигнала S(x) во многом соответствуют преобразованию Фурье, использующему оконную функцию w(x – a) [6, 7]. При этом ВП, используя базисную функцию ψ(a,b)(x), определяется следующим равенством:
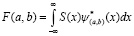. (1)
В системах OFDM вместо БПФ и ОБПФ предлагается использовать ДВП, которые позволяют снизить искажения сигнала S(x) при выполнении обратного преобразования, а также уменьшить избыточность, которая присуща ВП [8, 9]. Тогда входной сигнал можно представить в виде суммы двух функций φ(x) и ψ(x). Первая функция является масштабирующей, а вторая – вейвлет-функцией. При этом используются соответствующие коэффициенты. При масштабирующей функции φ(x) применяются коэффициенты приближения aj0(k), при функции ψ(x) – вейвлет-коэффициенты dj(k). Тогда имеем
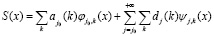. (2)
В этом случае коэффициенты имеют вид
, 
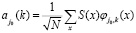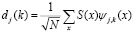, (3)
где N – число отсчетов S(x); k = 0, 1, … N–1.
Известно, что ДВП успешно используются в кратномасштабных анализах сигналов, что показано в [6–8]. Это связано с тем, что ДВП локализованы как во временной, так и в частотной областях. Именно данное свойство послужило отправной точкой применения ДВП в системах OFDM. Однако, несмотря на данные достоинства, ДВП не позволяют достичь предельно возможного уровня скорости передачи информации. Это связано с тем, что коэффициенты ДВП представляют собой иррациональные числа. Из-за этого увеличивается время на реализацию операций умножения, а также происходит накопление ошибок округления. Одним из перспективных подходов, позволяющим устранить данный недостаток, является переход к целочисленным дискретным вейвлет-преобразованиям, реализуемым в полях Галуа. Данные ЦДВП, обладая свойствами ДВП, могут обеспечить повышение скорости обработки сигналов за счет использования табличной организации вычислений. В этом случае операции сложения, вычитания и умножения отсчетов входного сигнала на коэффициенты ЦДВП заменяются операциями выборки из LUT-таблиц. Для целочисленных дискретных вейвлет-преобразований, выполняемых в поле Галуа GF(М), базисные функции будут определяться
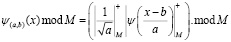. (4)
где ψ(x) – вейвлет-функция.
Для восстановления входного сигнала S(x) необходимо выполнить обратное ЦДВП. В этом случае реализуется выражение
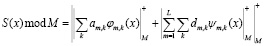. (5)
где L – высший уровень разложения ЦДВП.
В настоящее время широкое распространение получили ДВП Добеши [7–9]. Такой выбор определяется свойствами данного ДВП. Во-первых, ДВП Добеши присуще свойство гладкости. Во-вторых, данное ДВП имеет компактный носитель, обладающий свойством ортогональности. В-третьих, ДВП Добеши использует две функции – масштабирующую и вейвлет-функцию. Поэтому вычисление ДВП Добеши может быть организовано с банка фильтров, используя быстрый алгоритм вычисления ДВП. Рассмотрим выполнение ДВП Добеши-4 в GF(M). Известно, что данное преобразование использует коэффициенты вида
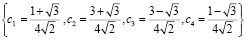. (6)
Для реализации ДВП в конечном поле умножим данные числа на коэффициент масштабирования В и возьмем целую часть результата Это позволяет представить коэффициенты Добеши в виде элементов поля GF(M). При реализации ЦДВП Добеши-4 в GF(M) при поступлении вектора, состоящего из восьми отсчетов, получаем следующие аппроксимирующие коэффициенты:
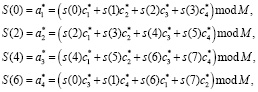(7)
где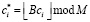 
, где В – коэффициент масштабирования; i = 1, 2, 3, 4.
Тогда детализирующие коэффициенты ДВП Добеши-4 в конечном поле
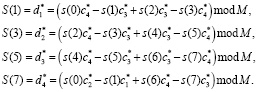(8)
Так как часть коэффициентов Добеши-4 представляет собой отрицательные числа, то предлагается весь диапазон элементов поля Галуа GF(M) разделить. Первый диапазон располагается от нуля до (M + 1) / 2. В данном диапазоне размещаются положительные числа. Второй диапазон поля Галуа предназначен для записи отрицательных результатов.
Анализ работ [6–9] показывает, что при вычислении ДВП используются банки фильтров, представляющих собой набор НЧ и ВЧ фильтров, импульсная характеристика определяется коэффициентами ДВП. Однако данный метод вычисления ДВП имеет существенный недостаток – относительно низкую скорость получения аппроксимирующих и детализирующих коэффициентов. Это связано с необходимостью проведения децимации сигналов. Устранить данный недостаток позволяет структурная модель базовой операции ДВП Добеши в GF(M), которая показана на рисунке.
Так как в качестве входных отсчетов и коэффициентов Добеши используются элементы поля Галуа, то для выполнения арифметических операций умножения, сложения и вычитания использовать LUT-таблицы.
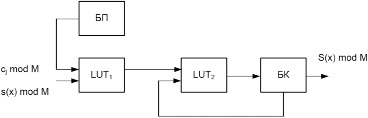
Структурная модель базовой операции ДВП Добеши в GF(M)
Первая LUT-таблица предназначена для выполнения операции умножения входного отсчета s(x) на соответствующий коэффициент ДВП в поле
,
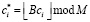где В – коэффициент масштабирования; i = 1, 2, 3, 4.
Коэффициенты для всех умножителей хранятся в блоке памяти (БП). Вторая LUT-таблица предназначена для выполнения операции сложения по модулю М. При этом используется блок коммутации (БК). Данное устройство работает в течение L тактов, где L – порядок ДВП Добеши.
Результаты исследования и их обсуждение
Для оценки эффективности применения разработанных моделей ДВП Добеши в полях Галуа был произведен сравнительный анализ с БПФ. В работе [10] показано, что в системе спутникового интернета StarLink применяются сигналы OFDM, поддерживающие 64 QAM. В системе OFDM применяется 64 QAM. Значит, размерность входного сигнала s(x), поступающего на вход модуляторов, составляет 8 бит. Пусть сигнал OFDM имеет общее число поднесущих, равное 52, из которых 48 поднесущих используется для передачи данных. В этом случае для генерации сигнала необходимо использовать 64-точечное БПФ. Тогда для вычисления БПФ необходимо выполнить 6 итераций базовой операции «бабочка». При этом каждая такая операция требует умножения двух комплексных чисел, а также их сложения и вычитания. В этом случае для реализации базовой операции «бабочка» необходимо выполнить 4 операции умножения и 6 операций сложения.
Рассмотрим выполнение ДВП Добеши-4 с использованием 8-разрядных входных данных. Представим коэффициенты ДВП в виде целых чисел. Для этого воспользуемся коэффициентом масштабирования В = 256. В результате получаем следующие коэффициенты, представленные в двоичном коде.
Таблица 1
Коэффициенты ДВП Добеши-4
|
Коэффициенты Добеши-4 |
В = 256 |
Двоичный код |
|
с1 = 0,683027 |
174 |
0010101110 |
|
с2 = 1,1830127 |
302 |
0100101110 |
|
с3 = 0,3169873 |
81 |
0001010001 |
|
с4 = –0,1830127 |
-46 |
1111010001 |
Пусть на вход поступают первые четыре отсчета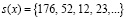 
. Найдем для данных отсчетов аппроксимирующий коэффициент
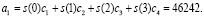
В этом случае детализирующий коэффициент будет равен
.
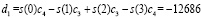После полученный результат можно сдвинуть вправо на восемь разрядов. В результате имеем значения аппроксимирующего и детализирующих коэффициентов, если бы вычисления происходили в позиционной системе счисления.
Рассмотрим выполнение ДВП Добеши-4, представленное в поле Галуа. В качестве характеристики поля Галуа выбираем простое число М = 262147. Данное значение числа выбрано из условия, что положительные результаты не должны превысить первый диапазон элементов поля, который размещается от 0 до 131073. При этом отрицательные результаты должны находиться во втором диапазоне. В табл. 2 представлены значения коэффициентов Добеши-4, приведенные в поле GF(262147).
Таблица 2
Коэффициенты ДВП Добеши-4 в поле GF(262147)
|
Коэффициенты Добеши-4 |
В = 256 |
Коэффициенты Добеши-4 в поле GF(262147). |
|
с1 = 0,683027 |
174 |
|
|
с2 = 1,1830127 |
302 |
|
|
с3 = 0,3169873 |
81 |
|
|
с4 = –0,1830127 |
-46 |
|
Найдем для исходных четырех отсчетов аппроксимирующий коэффициент.
.
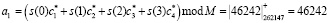Так как а1 < М/2, то результат считается положительным. Тогда детализирующий коэффициент в GF(262147) будет равен
.
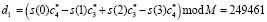Так как d1 > М/2, то коэффициент является числом отрицательным. Получаем, что
.
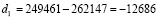Таблица 3
Временные затраты на ортогональные преобразования сигналов
|
Разработанные математические модели |
Операция «бабочка» |
БПФ |
||
|
Добеши-4 |
Добеши-6 |
Добеши-8 |
||
|
240 нс |
360 нс |
480 нс |
84 нс |
468 нс |
Результаты, полученные в позиционной системе счисления и в конечном поле Галуа совпали. Для проведения сравнительной оценки временных затрат на выполнение ортогонального преобразования сигналов с использованием БПФ и ДВП в конечных полях использовался метод RTL – моделирования работы ПЛИС. В качестве ПЛИС выбрана Kintex UltraScale xcku025-ffva1156-1. Программирование и исследование проводилось с помощью САПР Xilinx Vivado-HLS 2018. Результаты исследований представлены в табл. 3.
Полученные данные показывают, что использование разработанных математических моделей выполнения ДВП Добеши в конечном поле Галуа позволяет сократить время выполнения ортогонального преобразования сигналов. Так, при применении разработанной математической модели ДВП Добеши-6 время выполнения ортогонального преобразования сигналов сократилось по сравнению со временем реализации БПФ в 1,3 раза. А при использовании модели ДВП Добеши-4 временные затраты уменьшились в 1,95 раза. Таким образом, применение разработанных моделей ДВП Добеши в конечных полях приведет к сокращению временных затрат на генерацию сигнала OFDM. А это в свою очередь приведет к повышению скорости передачи информации в низкоорбитальных системах спутникового интернета.
Заключение
Для повышения скорости передачи информации в НССИ было предложено сократить временные затраты на генерацию сигнала OFDM за счет изменения вида ортогональных преобразований сигналов. В статье приведены математические модели выполнения ЦДВП Добеши в полях Галуа, применение которых позволяет сократить время выполнения ортогонального преобразования сигналов по сравнению с БПФ. Результаты исследования показали, что при применении математической модели ЦДВП Добеши 6 время выполнения ортогонального преобразования сигналов сократилось по сравнению со временем реализации БПФ в 1,3 раза. А при использовании модели ДВП Добеши 4 – в 1,95 раза. Таким образом, очевидно, что использование разработанных моделей ДВП Добеши в конечных полях уменьшает временные затраты на генерацию сигнала OFDM, что способствует повышению скорости передачи информации в НССИ.
Библиографическая ссылка
Калмыков И.А., Чистоусов Н.К., Калмыков М.И., Духовный Д.В., Юрданов Д.В. МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЕАЛИЗАЦИИ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЙ ДОБЕШИ В ЦЕЛОЧИСЛЕННЫХ ПОЛЯХ ГАЛУА // Современные наукоемкие технологии. – 2023. – № 2. – С. 71-76;URL: https://top-technologies.ru/ru/article/view?id=39526 (дата обращения: 21.11.2024).