Анализ надежности технических объектов позволяет оценить эффективность их работы и выявить уязвимые элементы в системах. Поэтому разработка моделей и методик оценки показателей безотказности является актуальной научно-технической задачей.
Для организаций, эксплуатирующих и проектирующих технические системы, существует необходимость в универсальной интегрированной среде моделирования надежности [1]. Как отмечают авторы статьи [1], для разработки такой среды необходима обширная библиотека разного рода моделей надежности.
Выбор методов оценки надежности технических систем необходимо осуществлять с учетом специфики анализируемого объекта [2]. Например, в работе [3] отмечается, что для инженеров необходим инструмент оценки надежности, в котором бы отражалась архитектура самого объекта. Модель надежности системы управления не может быть универсальной, так как необходимо учитывать не только архитектуру объекта, но и цель моделирования, доступные данные и др. Так, при разработке моделей надежности систем управления в работах [4, 5] объект исследования был разбит на подсистемы с учетом выполняемых функций.
Известным способом анализа надежности систем управления является применение метода анализа видов и последствий отказов (FMEA) [6, 7], но указанный инструмент не является достаточным и рассматривается как начальный этап оценки безотказности и безопасности объекта на этапе проектирования [8].
Предложенная нами модель рассматривает АСУ ТП в период эксплуатации. Но авторы [1, 3] отмечают, что оценка надежности эксплуатируемых объектов усложнена тем, что показатели надежности являются динамическими, и, следовательно, модель надежности должна использовать данные текущего момента функционирования объекта. Для решения данной проблемы в [1] предлагается метод, основанный на динамической байесовской сети, которая представляет типовую сеть Байеса в функции времени. В рассматриваемом методе время является еще одним рядом данных. Кроме того, применение динамических сетей Байеса позволяет просто и наглядно моделировать надежность и безопасность сложных объектов [9]. С учетом вышесказанного, при разработке модели надежности АСУ ТП необходимо учитывать функциональное назначение составляющих элементов (программные и аппаратные средства), архитектуру (нижний, средний и верхний уровни автоматизации) и динамику изменений в системе (суммарную наработку).
Целью исследования является разработка модели функциональной надежности АСУ ТП. При расчете функциональной надежности учитываются функциональные отказы, под которыми понимаются состояния объекта, при которых система не выполняет какую-либо функцию, например не осуществляет контроль или регистрацию технологического параметра. При функциональном отказе система может быть работоспособной.
Материалы и методы исследования
При моделировании надежности АСУ ТП используем динамическую сеть Байеса, которая позволяет интегрировать модели надежности двух подсистем: программной и аппаратной составляющих системы управления. Для создания сети в нашем случае узлы описываются математическими моделями в функции времени.
При разработке модели выделяем программную и аппаратную части, в последней учитываем уровни автоматизации (нижний, средний, верхний). Для указанных подсистем применяются различные средства анализа безотказности. Поэтому вначале создаем отдельно модель надежности программного обеспечения и модель надежности аппаратных средств (с выделением уровней автоматизации), в завершение объединяем полученные модели подсистем в динамическую сеть Байеса.
Модель надежности программных средств. Модель надежности программного обеспечения является частью модели надежности АСУ ТП. Для оценки надежности ПО применяются аналитические и эмпирические методы; используют математический аппарат теории вероятности [10] и математической статистики, теории Марковских цепей [11] и др. [12].
Так как создаваемая модель надежности АСУ ТП динамическая, то и модель надежности ПО должна быть динамической, например, базироваться на модели Шумана или Джелинского – Моранды.
Динамическая модель Шумана в нашем случае непригодна, так как требует знания числа команд на машинном языке в программе; в нашем случае такие данные получить проблематично, так как необходимо учесть ПО среднего и верхнего уровня автоматизации. Безусловно, модель Шумана при наличии исходных данных очень удобна.
Таким образом, при разработке модели надежности ПО использовали модель Джелинского – Моранды [13–15].
Модель Джелинского – Моранды использует данные о периодичности возникновения программных сбоев, которые легко отследить в процессе эксплуатации, и является «моделью роста надежности», так как при исправлении ошибок надежность ПО увеличивается. Данная модель при описании показателей безотказности использует экспоненциальный закон распределения. Функция надежности ПО имеет вид P(ti) = exp(–λi ∙ ti), где ti – момент времени после очередного (i – 1)-го восстановления; λi – интенсивность отказов (сбоев) программы на i-м интервале работы. Методика расчета интенсивности отказов ПО подробно изложена в литературе, например в [14].
Пример расчета. Для определения интенсивности отказов использованы данные за 198 суток (6,6 мес.) АСУ ТП дожимной насосной станции Южно-Аганского месторождения. Исходные данные по наработке получены с момента обновления ПО, составляют τ = [12, 30, 35, 37, 41, 43], сут. Возникшие после модернизации АСУ ошибки устранялись перезагрузкой ПО и внесением незначительных корректив в код. Ошибки (сбои) ПО, возникшие в течение суток после модернизации системы, не учтены как возникшие в результате пуско-наладочных мероприятий.
На основе данных рассчитана интенсивность отказов ПО на i = 7 интервале эксплуатации, она составила λ7 = 0,015 (1/сут). Функция вероятности безотказной работы (функция надежности) ПО на 7-интервале эксплуатации имеет вид: P(t) = exp(–0,015∙t).
Рис. 1. Структурная схема надежности канала связи по давлению
Модель надежности аппаратных средств. Для описания надежности аппаратных средств применяли метод, основанный на структурных схемах. При разработке структурных схем и математического описания надежности приняли следующие допущения:
− отказ любого элемента вызывает функциональный отказ АСУ ТП, то есть система не выполняет все требуемые функции;
− АСУ рассматривается в период нормальной эксплуатации, то есть для описания показателей безотказности элементов можно применять экспоненциальный закон распределения. Предельное состояние объекта не рассматриваем, так как в процессе эксплуатации АСУ ТП постоянно модернизируется или выполняется восстановление при проведении планового технического обслуживания (ТО) и ремонта; кроме того, составляющие АСУ элементы, как правило, неремонтопригодны, после отказа заменяются исправными;
− средства противоаварийной защиты (ПАЗ) не рассматриваются.
В связи с первым допущением отмечаем, что структурная схема надежности канала связи представляет собой основное (последовательное) соединение элементов. Упрощенная структурная схема для каналов связи нижнего уровня имеет вид: датчик – линия связи – исполнительный механизм. Для среднего/верхнего уровня: контроллер – линия связи – автоматизированное рабочее место (АРМ). Для примера на рис. 1 изображена структурная схема канала регулирования по давлению.
Для получения функции надежности каналов связи рассчитывается интенсивность отказов элементов по формуле λi = 1/Ti , где Ti – средняя наработка до отказа (определяется из паспортов оборудования). Интенсивность отказов канала связи определяется суммой λC = ∑ λ1, так как структурная схема надежности описывается основным соединением элементов.
Вероятность безотказной работы канала связи имеет вид:
.
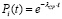Рассмотрим расчет надежности для АСУ дожимной насосной станции Южно-Аганского месторождения. На объекте функционируют сепарационные установки, насосный блок с двумя насосными агрегатами.
На основе структурной схемы канала регулирования давления в сепараторе (РС) (рис. 1) определена интенсивность отказов:
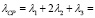
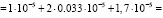
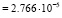(час–1).
Вероятность безотказной работы канала регулирования давления описывается выражением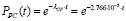 
.
Аналогичным образом рассчитываются показатели безотказности для других каналов связи:
− канал регулирования уровня в сепараторе (LC)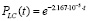 
;
− канал сигнализации по давлению в сепараторе (PA)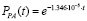 
;
− канал контроля давления на выкиде насоса (PI)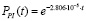 
;
− канал контроля температуры подшипников насоса (TI) (2 шт.)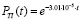 
;
− канал среднего/верхнего уровня (ПЛК+АРМ) PПЛК+АРМ(t)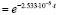
.
При разработке динамической модели надежности аппаратных средств принято следующее:
− техническое обслуживание (ТО) для элементов нижнего уровня автоматизации выполняется одновременно с периодичностью 6 мес. (согласно НТД техническое обслуживание должно проводиться не реже 1 раза в 5–7 мес.);
− периодичность ТО для средств автоматизации среднего и верхнего уровней составляет 12 мес.;
− после аварийного восстановления или ТО достигается исправное состояние системы;
− восстановление происходит мгновенно.
В примере расчета из-за отсутствия данных не учтены аварийные отказы и восстановления после них.
На рис. 2 представлены графики функции надежности для выделенных каналов связи АСУ на интервале наработки 135–240 суток.
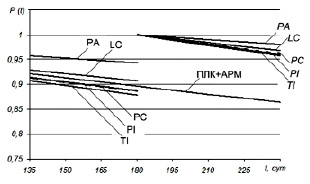
Рис. 2. Функция надежности для аппаратных средств АСУ
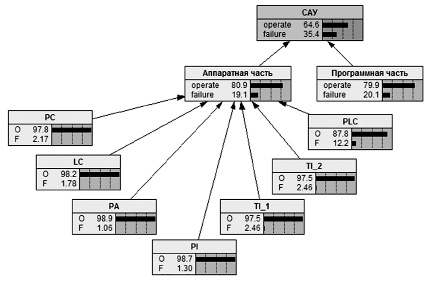
Рис. 3. Сеть Байеса для АСУ ДНС при наработке 213 суток
По графикам видно, что при наработке 180 суток (6 мес.), после планового ТО, каналы связи нижнего уровня восстановлены полностью: (PPC(180) = PLC(180) = PPA(180) = PPI(180) = PTI(180) = 1); при увеличении наработки надежность снижается. Подсистема «ПЛК+АРМ» не восстанавливается на рассматриваемом интервале эксплуатации, ее надежность снижается на данном интервале.
Модель надежности АСУ ТП на базе динамической сети Байеса. Для оценки безотказности АСУ дожимной насосной станции Южно-Аганского месторождения разработана динамическая сеть Байеса, исходные данные для которой определяются по разработанным моделям надежности ПО и аппаратных средств. Из полученных выше моделей надежности для ПО и аппаратных средств используются выражения функции надежности вида Pi(t) = exp(λ1∙t), где i – элемент системы.
На рис. 3 представлена сеть Байеса с данными для момента непрерывной работы 213 суток (15 суток 7-го интервала работы ПО).
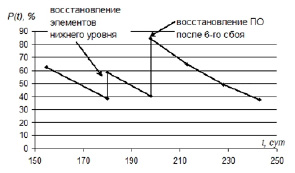
Рис. 4. График функции надежности АСУ ТП
На рисунке 3 использованы следующие обозначения: «O/operate» – вероятность безотказной работы объекта, «F/failure» – вероятность отказа объекта. Для данного момента времени наименьшим значением вероятности безотказной работы характеризуется ПО РПО(213) = 79.9%, то есть с большой вероятностью может произойти сбой; среди аппаратных средств наиболее уязвимым местом АСУ является канал связи среднего/верхнего уровня (PLC) РPLC(213) = 87.7%.
На основе предложенной сети Байеса можно определить вероятность безотказной работы АСУ ТП в функции наработки. На рис. 4 представлен график изменения функции надежности АСУ ТП на интервале наработки 150–250 суток после модернизации. На диаграмме отражено восстановление элементов системы управления при ТО аппаратных средств нижнего уровня автоматизации (при 180 сутках) и после 6-го сбоя программного обеспечения (при 198 сутках).
Заключение
В статье предложена модель надежности, которая позволяет комплексно оценивать безотказность программно-аппаратной системы, какой является АСУ ТП. Разработанная модель является динамической и позволяет оценивать функцию надежности в процессе эксплуатации технических объектов.
Предложенная модель надежности рассматривает аппаратно-програмную систему в период нормальной эксплуатации, при которой отсутствуют износовые отказы. Тем не менее данную модель можно применить и для процесса приработки и для периода старения системы: в этом случае необходимо применить логнормальное или распределение Вебулла для описания наработки до отказа аппаратных средств.
Достоинствами разработанной модели являются: соблюдение архитектуры АСУ, визуальная реализация в виде сети Байеса, простота получения данных для модели, учет динамики изменения показателей надежности во времени.
Предложенную модель в дальнейшем можно уточнить следующими способами:
− расчетом интенсивности отказов аппаратных средств на основе статистических данных;
− выделением уровней автоматизации для ПО;
− выделением в модели надежности ПО различного типа сбоев, в том числе нарушения безопасности.
Библиографическая ссылка
Гладких Т.Д. МОДЕЛЬ НАДЕЖНОСТИ АВТОМАТИЗИРОВАННОЙ СИСТЕМЫ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМ ПРОЦЕССОМ // Современные наукоемкие технологии. – 2023. – № 2. – С. 30-35;URL: https://top-technologies.ru/ru/article/view?id=39520 (дата обращения: 02.05.2024).