Существующие способы компьютерного вычисления функций не универсальны относительно вида функции, точности приближения и временной сложности. Библиотеки программ их вычисления имеют ограниченные наборы функций, ограниченную точность, наиболее сложные из них часто предоставляют реализовать пользователю. Программные реализации алгоритмов вычисления функций неоднородны. В случае параллельных вычислений это увеличивает такт синхронизации яруса вычисления функций. Компьютерные библиотеки не гарантируют управление погрешностью вычисления входящих в них функций. Данное состояние вопроса имеет следствие, которое относится к приближенному решению обыкновенных дифференциальных уравнений (ОДУ). Сложность вычислительного алгоритма приближенного решения системы ОДУ определяется количеством обращений к правой части системы. Избытка обращений стараются избегать именно из-за наличия в правой части выражений, иногда в большом количестве включающих функции, часто с трудоемкими алгоритмами вычисления. Отсюда возникают проблемы накопления погрешности по длине промежутка решения ОДУ, проблемы многократного воспроизведения решения. Помимо того, возникает проблема исследования математических свойств решения задачи по его численному приближению. Подход к техническому решению данных трудностей приобретает единообразный характер, если алгоритмы вычисления функций и численного интегрирования ОДУ строить на основе кусочной интерполяции. В статье ставится задача раскрыть взаимосвязи и возможности кусочной интерполяции на примерах компьютерных программ вычисления специальных функций и решения задачи Коши для ОДУ. Требуется показать, что высокая точность и одновременно малая временная сложность вычислительных алгоритмов достигаются на основе хранения в памяти компьютера коэффициентов интерполяционных полиномов в структурном соответствии подынтервалам, на которых они построены. Особая эффективность метода достигается для случая многократного воспроизведения функций и решений ОДУ. Предложенные кусочно-интерполяционные приближения являются непрерывными как для решения задачи Коши, так и для производной от решения. Способ хранения коэффициентов фактически является способом хранения этих непрерывных приближений, приближения быстро восстанавливаются без повторного решения задачи, и по ним можно выполнить аналитическое исследование особенностей решения (с элементами «автоматизации»).
Цель исследования – раскрыть методику построения, дать обоснование, показать математическое и техническое значение хранимой непрерывной кусочной интерполяции функций одной действительной переменной и решений задачи Коши для ОДУ применительно к многократному воспроизведению. Требуется выполнить численные эксперименты, представить результаты и подтверждающие коды программ.
Описание метода кусочной интерполяции
Для интерполяции функции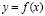 
, 
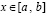, полином Лагранжа с равноотстоящими узлами интерполяции xj, 
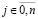, можно записать в виде [1]:
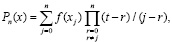
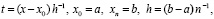
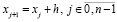. (1)
Преобразование числителя дроби
,
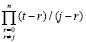записываемого в виде
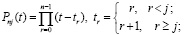, (2)
влечет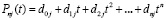 
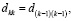
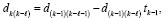
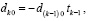
, где коэффициенты восстанавливаются по корням из (2) с помощью алгоритма [2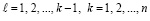, 3]:
. (3)
В результате
, 
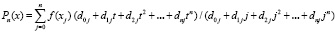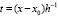. (4)
Если в (4) собрать коэффициенты при равных степенях, то
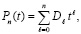
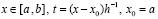, (5)
Dℓ – результат приведения подобных,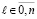 
.
В методе кусочной интерполяции (1)–(5) реализуется на малых подынтервалах [ai, bi] равной длины с общими границами разбиения отрезка [a, b]:
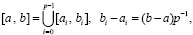
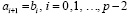. (6)
Описанные выше преобразования выполняются на каждом подынтервале. Полученные в результате полиномы (5) и их коэффициенты отмечаются индексом подынтервала:
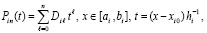
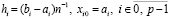. (7)
Здесь и ниже индекс i в обозначении hi может создать впечатление, что расстояние между узлами интерполяции меняется от подынтервала к подынтервалу. Это не так – согласно (6), (7) здесь и ниже
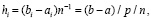
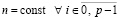, (8)
индекс i в hi принят для идентификации отличия hi от h на [a, b] при отсутствии разбиения на подынтервалы (p – 1 = 0). Более правильным было бы обозначение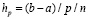 
.
С учетом (8) для произвольного х ∈ [a, b] номер подынтервала, которому принадлежит x, х ∈ [ai , bi] , вычисляется как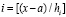 
, или,
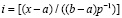, (9)
где [α] – целая часть числа α. Если коэффициенты Diℓ полиномов из (7) зафиксированы и хранятся в памяти, то номер подынтервала является адресом обращения к памяти для их считывания.
После считывания вычисление полинома, приближающего функцию, выполняется с применением схемы Горнера за время
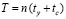, (10)
где ty – время бинарного умножения, tc – время бинарного сложения. При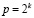 
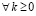справедлива оценка [4]:
,
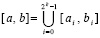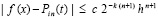
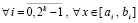(11)
где c = const,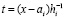 
,
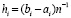– шаг интерполяции на [ai, bi], 
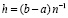. Оценка показывает, что точность приближения растет с уменьшением длины подынтервала (при фиксированной степени полинома), что и полагается в основу кусочной интерполяции.
Аналогичные преобразования можно выполнить в интерполяционном полиноме Ньютона. Для интерполяции функции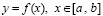 
, полином Ньютона с равноотстоящими узлами интерполяции xj, 
, 
, 
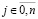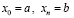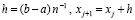, записывается в виде
,
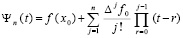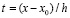, (12)
где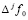 
– конечная разность j-го порядка в узле x0. Чтобы привести подобные с применением алгоритма (3), в произведении 
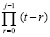следует положить 
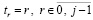, восстановить по данному алгоритму коэффициенты каждого такого полинома, затем во всех n слагаемых (12) сложить числовые значения при равных степенях. В результате полином (12) примет вид
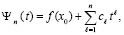
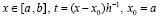. (13)
Если такое преобразование выполнить на каждом подынтервале из (6), то в индекс коэффициентов (13) включается номер подынтервала. Для полинома (12) получится
,
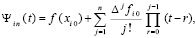
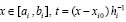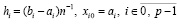.(14)
и для полинома (13) соответственно
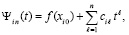
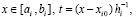
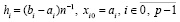. (15)
После считывания коэффициентов время вычисления оценивается из (10). Формально точность приближения такая же, как в (11) [1].
Основные особенности и свойства данной разновидности кусочной интерполяции.
Во-первых, поскольку в число узлов интерполяции на каждом подынтервале включаются границы подынтервала, а узловые значения на общей границе совпадают,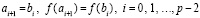 
, то получаемое приближение функции, 
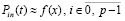, аналогично, 
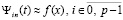, непрерывно на всем отрезке приближения [a, b] из (6).
Во-вторых, вместе с приближением функции одновременно получается приближение производной,
,
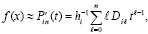
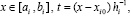
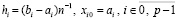аналогично,
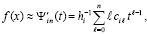
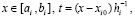
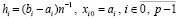, (16)
при этом приближение производной непрерывно на каждом подынтервале.
В-третьих, одновременно приближается первообразная:
,
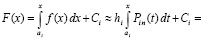
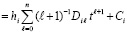где
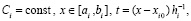
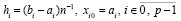
(аналогично, для полинома Ньютона). При этом значение произвольной постоянной Ci на каждом подынтервале [ai, bi] можно всегда выбирать так, что первообразная будет непрерывной функцией на всем отрезке [a, b]. Ниже это используется для приближенного решения задачи Коши для обыкновенных дифференциальных уравнений (ОДУ). Выше n можно было выбрать априори, например, с целью минимизации времени вычисления в априори заданных границах погрешности приближения. Однако степень полинома можно выбрать программно («автоматически»), например, с целью минимизации погрешности приближения в заданных границах времени вычисления [4]. Для многократного воспроизведения функций, производных и решений ОДУ наиболее ценным свойством является возможность запоминания коэффициентов в соответствии номерам подынтервалов в памяти компьютера (или на внешних носителях). Чтобы воспроизвести функцию (производную, решение ОДУ), достаточно обратиться к хранимому массиву коэффициентов в памяти по номеру подынтервала как по адресу, считать коэффициенты и за время (10) вычислить приближение. Для этого не требуется заново строить приближение или последовательно проходить весь промежуток решения ОДУ.
Кусочная интерполяция специальных функций. Гамма-функция
Выполнить интерполяцию можно по любым дискретным значениям в узлах интерполяции. Применение рассматриваемого метода к суперпозициям элементарных функций обсуждается в [3, 5]. Ниже обсуждается приближение трех наиболее важных специальных функций. Приближение гамма-функции в случае вещественного аргумента строится на отрезке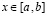 
, отделенном от особенностей, оговаривается вычисление в более общем случае. Вначале для задания узловых значений используется формула [6, с. 361]:
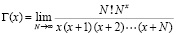. (17)
В качестве приближения к пределу выбирается некоторое большое значение N. Вычисление выполняется с эквивалентным видоизменением (17)
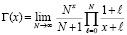, (18)
чтобы ограничить влияние факториального роста, выводящего за границы числового диапазона. Из (18)
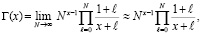
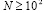, (19)
где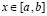 
, 
.
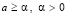Пусть [a, b] = [0.5, 1]. Согласно численному эксперименту в этом случае выбор N = 106 обеспечивает вычисление Г(х) с абсолютной погрешностью порядка ε ≤ 10–7 (здесь и ниже с точностью до коэффициента меньшего 10). Выбор N = 107 обеспечивает вычисление Г(х) с точностью до ε ≤ 10–8 (с той же оговоркой). Можно предположить, что выбор в (19) N = 10k, k ≥ 2, обеспечивает точность приближения порядка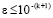 
. Ниже приводится программная реализация метода с автоматическим выбором числа подынтервалов (Delphi), которая реализует процесс вычисления коэффициентов для данной разновидности кусочно-полиномиальной аппроксимации с применением (12), (15):
program pi_newton_fixed_n_gamma; {$APPTYPE CONSOLE} uses SysUtils, Math;
const a0=0.5; b0=1; {границы отрезка приближения}
abs_error=1.0e-6; {априори заданная граница абсолютной погрешности приближения}
k_max=10; {2^k_max – правая граница диапазона вариации числа подынтервалов}
n_fix=2; {фиксированное значение степени интерполяционных полиномов для всех подынтервалов}
FILEPATH = ‘D:\coeff.bin’; {путь к файлу для записи коэффициентов полиномов, аппроксимирующих функцию} type M=array[0..n_fix] of extended; MM=array[0..n_fix,0..n_fix] of extended;
var d:MM; myfile:file of M; dd:M;
function f(x:extended):extended; var r, n_max:int64; p:extended;
begin n_max:=round(1/abs_error); p:= 1/x; r:= 1; while r <= n_max-1 do begin p:=p*r/(x+r); r:=r+1;end;
p:=p*exp(x*trunc(log10(1/abs_error))*ln(10)); f:=p; end;
procedure Konech_Raznoct(n:byte;a00,h: extended; var dy:MM); var i,k:byte;x:M;
begin for i:=0 to n do x[i]:=a00+i*h; for i:=0 to n-1 do dy[1,i]:=f(x[i+1])-f(x[i]);
for k:=2 to n do for i:=0 to n-k do dy[k,i]:=dy[k-1,i+1]-dy[k-1,i] end;
procedure Viet(n:byte;var d:MM); var q:MM;k,i,j:byte;
begin q[1,1]:=1; q[1,0]:=0; for k:=2 to n do begin q[k,0]:=-q[k-1,0]*(k-1); for i:=1 to k-1 do
q[k,k-i]:=q[k-1,k-i-1]-q[k-1,k-i]*(k-1); q[k,k]:=q[k-1,k-1] end; for j:=1 to n do for i:=0 to j do d[i,j]:=q[j,i]
end;
procedure pi_Newton(print:boolean; n,k:byte; var cond:boolean); var xpr,t,hpr,s,p,h:extended; pp:integer;
dy: MM; a00, b00, vel_podint: extended; i,j,l: byte; b,a: M; n_pod:int64;
begin vel_podint:=(b0-a0)/exp(k*ln(2)); a00:=a0; b00:=a00+vel_podint; n_pod:=0;
while a00<=b0-vel_podint do begin h:=(b00-a00)/n; Konech_Raznoct(n,a00,h,dy);
pp:=1; for j:=1 to n do begin pp:=pp*j; b[j]:=dy[j,0]/pp; end; a[0]:=f(a00);
for l:=1 to n do begin s:=0; for j:=l to n do s:=s+d[l,j]*b[j]; a[l]:=s end;
if print then begin {вывод на экран и запись в файл коэффициентов аппроксимирущих полиномов}
writeln(‘n_pod=’,n_pod); for i:= 0 to n do writeln(‘a[‘,i,’]=’,a[i]);
for i := 0 to n_fix do dd[i]:=a[i]; write(myfile, dd); end
else begin xpr:=a00; hpr:=h/33; while xpr<=b00 do begin t:=(xpr-a00)/h; p:=a[n];
for i:=n-1 downto 0 do p:=p*t+a[i]; if abs(p-f(xpr))>abs_error then cond:=false; xpr:=xpr+hpr end; end;
a00:=a00+vel_podint; b00:=a00+vel_podint; inc(n_pod); end; end;
procedure vpi_f(a0,b0:extended); var k:byte; cond:boolean;
begin k:=0; repeat cond:=true; pi_Newton(false,n_fix,k,cond);
if cond=true then begin writeln(‘k=’,k); pi_Newton(true,n_fix,k,cond); exit; end else inc(k);
until k>k_max; end;
begin AssignFile(myfile,FILEPATH); Rewrite(myfile); Viet(n_fix,d); vpi_f(a0,b0); CloseFile(myfile);
readln; end.
Границы отрезка приближения задаются значениями a0, b0. Степень полинома n (в программе n_fix) может быть произвольной. В данном случае выбрано n = 2. Число подынтервалов p = 2k определяется программно (алгоритм отдельно дан в [5]) из диапазона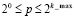 
, значение константы k_max определяется пользователем. Для априори заданной границы абсолютной погрешности (abs_error) выбирается наименьшее k, при котором эта граница погрешности не превышается во всех проверочных точках (в программе шаг проверки hpr: = h/33, где h – расстояние между узлами интерполяции на подынтервале). Интерполируемую функцию (в данном случае приближение гамма-функции (19)) формирует подпрограмма-функция с заголовком function f(x: extended): extended. Рассчитанные коэффициенты кусочно-полиномиальной аппроксимации сохраняются в типизированном файле (путь к файлу задается значением константы FILEPATH).
После создания файла хранимых коэффициентов функция (приближение гамма-функции) на фиксированном отрезке может воспроизводиться неограниченное количество раз. Это выполняется с помощью схемы Горнера после считывания коэффициентов из файла с адресацией (9):
program calc_func; {$APPTYPE CONSOLE} uses SysUtils, Math;
const aa=0.5; bb=1; n=2; k=6; {параметры приближения}
xpr=0.5+1/21; fpr=1.62283728597856626070; {проверочная точка и точное значение функции в ней}
FILEPATH1=’D:\coeff.bin’; {путь к файлу, в котором хранятся значения коэффициентов полиномов, аппроксимирующих функцию} var t,hh,h: extended; rr: integer;
function f(x: extended): extended; type Coeff = array[0..n] of extended; var myfile: file of Coeff; dd:Coeff;
function gorner (const dd:Coeff): extended; var pp:extended; i:integer;
begin pp:=dd[n]; for i:=1 to n do pp:=pp*t+dd[n-i]; gorner:=pp; end;
begin AssignFile(myfile,FILEPATH1); Reset(myfile);
if x<bb then rr:=trunc((x-aa)/hh) else rr:=trunc((x-aa)/hh)-1;
seek(myfile,rr); read(myfile,dd); t:=(x-(aa+rr*hh))/h; f:=gorner(dd); CloseFile(myfile); end;
begin hh:=(bb-aa)/power(2,k); h:=hh/n;
writeln (‘xpr=’,xpr,’; f(xpr)=’,f(xpr),’; pogr=’,abs(f(xpr)-fpr)); readln; end.
Результат работы программы:
Xpr = 5.47619047619048E-0001; f(xpr) = 1.62283766571833E+0000; pogr = 3.79739760851755E-0007
В этом варианте время воспроизведения гамма-функции измеряется временем двух умножений со сложениями. Для представленного примера число хранимых коэффициентов p(n + 1) = 192 (p = 26, n = 2). Повышение степени интерполяционных полиномов снижает число подынтервалов при фиксированном значении порядка погрешности (в примере 10–7): для n = 3 – p = 24, число коэффициентов p(n + 1) = 64; для n = 4 – p = 24, число коэффициентов p(n + 1) = 40; для n = 5 – p = 22, число коэффициентов p(n + 1) = 24; для n = 9 – p = 20, число коэффициентов p(n + 1) = 10.
При относительно небольшом количестве коэффициентов их значения могут располагаться непосредственно в разделе констант в виде двумерного массива. Тогда программа вычисления функции примет вид
program Newton_Gamma_n5_k2_const; {$APPTYPE CONSOLE}
uses SysUtils;
const aa=0.5; bb=1; hh=0.125; n=5; h=hh/n; Gamma121 = 1.62283728597856626070;
Pr_Gamma121 = -2.833470062096042329648;
var x, t: extended; i,rr: integer; Gammaf, Proiz_Gamma: extended;
procedure Gamma(x: extended; var Gammaf, Proiz_Gamma: extended);
type vec0=array[0..3,0..5] of extended;
const dd:vec0=
((1.77245407246226E+0000, -8.70039026866722E-0002, 4.86441678445746E-0003,
-2.43047087093533E-0004, 1.09329982158107E-0005, -3.13024140892727E-0007),
(1.43451901619824E+0000,-5.20980148280167E-0002,2.46971348186693E-0003,
-9.90748736884621E-0005, 3.71270172655088E-0006,-9.31331599597475E-0008),
(1.22541681734799E+0000,-3.32656757828449E-0002, 1.42460352695277E-0003,
-4.71653402909723E-0005, 1.52098151578120E-0006, -3.39377617028745E-0008),
(1.08965241701325E+0000, -2.19024394932337E-0002, 9.02997990859843E-0004,
-2.49226355961744E-0005, 7.11601360512539E-0007, -1.42690302017059E-0008));
function gorner11 (var rr: integer; const dd:vec0): extended;
var pp:extended;
begin pp:=dd[rr,n]; for i:=1 to n do pp:=pp*t+dd[rr,n-i]; gorner11:=pp; end;
function gorner12 (var rr: integer; const dd:vec0): extended;
var pp:extended;
begin pp:=dd[rr,n]*n/h; for i:=1 to n-1 do pp:=pp*t+dd[rr,n-i]*(n-i)/h; gorner12:=pp; end;
begin if x<1 then rr:=trunc((x-aa)/hh) else rr:=trunc((x-aa)/hh)-1; t:=(x-(aa+rr*hh))/h;
Gammaf:=gorner11(rr,dd); Proiz_Gamma:= gorner12(rr,dd); end;
begin
x:=0.5+1/21; Gamma(x, Gammaf, proiz_Gamma);
writeln (‘x= ‘,x,’ ; ‘,’ Gamma(x)=’,Gammaf,’ ‘, ‘; ‘,’ pogrechnost=’,Gammaf-Gamma121);
writeln (‘x= ‘,x,’ ; ‘,’Proiz_Gamma(x)=’,Proiz_Gamma,’ ‘, ‘; ‘,’ pogrechnost=’,Proiz_Gamma-Pr_Gamma121);
readln;
end.
Результат работы программы:
x=5.47619047619048E-0001; Gamma(x)= 1.62283747031041E+0000; pogrechnost=1.84331845806771E-0007
x=5.47619047619048E-0001; Proiz_Gamma(x)=-2.83346339759517E+0000; pogrechnost=6.66450086904261E-0006
С повышением степени полинома воспроизводимой является не только сама функция, но и производная от нее согласно (16). В данном примере это выполняется с использованием подпрограммы-функции с заголовком function gorner12 (var rr: integer; const dd:vec0): extended; (схема Горнера для производной от полинома). Для контроля погрешности приближения в качестве эталонного значения гамма-функции и ее производной приняты значения, полученные в результате запросов Gamma(0.5+1/21) и Gamma(0.5+1/21)*digamma(0, 0.5+1/21) в базе знаний Wolfram|Alpha [7]. Выражение производной от гамма-функции через произведение гамма-функции и дигамма-функции использовано с целью получить в качестве эталона наиболее высокую точность приближения (в Wolfram|Alpha результат непосредственного вычисления производной от гамма-функции представляется лишь шестью значащими цифрами).
С учетом (10) время вычисления гамма-функции с данной точностью приближения 5(ty + tc), ее производной – 4(ty + tc). Согласно численному эксперименту при использовании полинома Лагранжа с такими же параметрами алгоритма (в пределах погрешности порядка 10–7) достигается такая же точность приближения, как у полинома Ньютона, за то же время вычисления, что соответствует известному положению теории интерполяции [1]. Ближайшей целью будет получить более высокую точность воспроизведения гамма-функции за время 5(ty + tc) и ее производной за время 4(ty + tc). Чтобы этого достигнуть на основе (17)–(19), нужны более мощные по сравнению с персональным компьютером вычислительные ресурсы. Тем не менее показать принципиальную возможность решения задачи можно, обратившись к Wolfram|Alpha. Из этой базы можно извлечь значения гамма-функции с 20 верными значащими цифрами мантиссы [7]. Такие значения по отдельности заносятся в раздел констант программы в качестве узловых значений интерполяционного полинома Ньютона (14) степени n = 5, по n + 1 = 6 значений в соответствии каждому номеру подынтервала. По-прежнему [a, b] = [0.5, 1]. Число подынтервалов выбирается равным p = 64. Далее, программа без изменения описанного выше алгоритма на каждом подынтервале преобразует полином Ньютона (14) к виду (15), выдавая аналогично предыдущему по n + 1 = 6 числовых коэффициентов полинома в соответствии номеру подынтервала и показателю степени слагаемого в (15). Приводимая непосредственно ниже программа выводит вычисленные коэффициенты на экран и сохраняет их в типизированный файл по адресу ‘D:\gamma_n5_k6.bin’
program FPI_Newton_fixed_n5_k6_Gamma_wolfram; {$APPTYPE CONSOLE}
uses SysUtils, Math;
const k_fix=6; k_pod=64; n_fix=5; a0=0.5; b0=1;
FILEPATH = ‘D:\gamma_n5_k6.bin’;
type M=array[0..n_fix] of extended; MM=array[0..n_fix,0..n_fix] of extended;
var d: MM; k_output:integer;
type Coeff = array[0..n_fix] of extended; var myfile: file of Coeff; dd:Coeff;
function f(rr,ii:integer):extended;
type M_Coef = array[0..k_pod-1] of Coeff;
const Gammawolf: M_Coef =
((1.77245385090551602730,1.76703494882192059810,1.76165372540981521613,
1.75630982590783545747,1.75100289997491963006,1.74573260162213649936),
(1.74573260162213649936,1.74049858914576889878,1.73530052506162633201,
1.73013807604056033088,1.72501091284515696978,1.71991871026758155902),
………………………………………………………………………………………..
(1.00926398471568630315,1.00831524753567991035,1.00737153250209826800,
1.00643281760979125714,1.00549908100317067122,1.00457030097503136954),
(1.00457030097503136954,1.00364645596538367193,1.00272752456029687067,
1.00181348549075373742,1.00090431763151590432,1.00000000000000000000));
begin f:=Gammawolf[rr,ii]; end;
procedure Konech_Raznoct(n_pod,n:byte;a00,h: extended; var dy:MM);
var i,k:byte;x:M;
begin for i:=0 to n do x[i]:=a00+i*h; for i:=0 to n-1 do dy[1,i]:=f(n_pod,i+1)-f(n_pod,i);
for k:=2 to n do for i:=0 to n-k do dy[k,i]:=dy[k-1,i+1]-dy[k-1,i] end;
procedure Viet(n:byte;var d:MM);
var q:MM;k,i,j:byte;
begin q[1,1]:=1; q[1,0]:=0; for k:=2 to n do begin q[k,0]:=-q[k-1,0]*(k-1); for i:=1 to k-1 do
q[k,k-i]:=q[k-1,k-i-1]-q[k-1,k-i]*(k-1); q[k,k]:=q[k-1,k-1] end; for j:=1 to n do for i:=0 to j do d[i,j]:=q[j,i] end;
procedure pi_Newton(n,k:byte);
var s,h:extended; factorial:integer;
dy: MM; a00,b00,vel_podint: extended; i,j,l: byte; b,a: M; n_pod:int64;
begin
vel_podint:=(b0-a0)/exp(k*ln(2)); a00:=a0; b00:=a00+vel_podint; n_pod:=0; while a00<=b0-vel_podint do
begin
h:=(b00-a00)/n; Konech_Raznoct(n_pod,n,a00,h,dy);
factorial:=1; for j:=1 to n do begin factorial:=factorial*j; b[j]:=dy[j,0]/factorial; end;
a[0]:=f(n_pod,0); for l:=1 to n do begin s:=0; for j:=l to n do s:=s+d[l,j]*b[j]; a[l]:=s end;
writeln(‘ n_pod=’,n_pod); for i:= 0 to n do writeln(‘a[‘,i,’]=’,a[i]); for i := 0 to n do dd[i]:=a[i]; write(myfile, dd);
readln; a00:=a00+vel_podint; b00:=a00+vel_podint; n_pod:=n_pod+1; end; end;
begin
AssignFile(myfile,FILEPATH); Rewrite(myfile);
Viet(n_fix,d); pi_Newton(n_fix,k_fix); CloseFile(myfile); writeln(‘The End’); readln;
end.
Результат работы программы:
n_pod=0 n_pod=1
a[0]= 1.74573260162214E+0000 a[0]= 1.77245385090552E+0000
a[1]=-5.25209881756097E-0003 a[1]=-5.43786079183873E-0003
a[2]= 1.81427619631266E-0005 a[2]= 1.90187708044359E-0005
a[3]=-5.65959203444299E-0008 a[3]=-6.02518533339603E-0008
a[4]= 1.75668548099051E-0010 a[4]= 1.89860303427467E-0010
a[5]=-5.17960884866981E-0013 a[5]=-5.68102291735537E-0013
………………………………………………………………….......
n_pod=62 n_pod=63
a[0]= 1.00926398471569E+0000 a[0]= 1.00457030097503E+0000
a[1]=-9.51255625895055E-0004 a[1]=-9.26308937770043E-0004
a[2]= 2.52214482783028E-0006 a[2]= 2.46750315598351E-0006
a[3]=-3.70525932792730E-0009 a[3]=-3.58110871355065E-0009
a[4]= 6.32998349826685E-0012 a[4]= 6.08444119198047E-0012
a[5]=-9.82371555340959E-0015 a[5]=-9.36553352232083E-0015
Непосредственно ниже приводится программа, которая, аналогично программе calc_func, считывает коэффициенты полиномов из файла ‘D:\gamma_n5_k6.bin’, созданного предыдущей программой, и вычисляет значение полинома для заданного значения независимой переменной:
program calc_fun_deriv_gamma_wolf; {$APPTYPE CONSOLE} uses SysUtils, Math;
const aa=0.5;bb=1; n=5; k=6; FILEPATH=’D:\gamma_n5_k6.bin’;
{проверочная точка и точные значения функции и производной в данной точке
для вычисления абсолютной погрешности приближения}
xpr=0.5+1/21; f_pr=1.62283728597856626070; proiz_pr=-2.833470062096042329648;
var t,hh,h: extended; f,proiz: extended; rr: integer;
procedure calc(x: extended); type Coeff = array[0..n] of extended; var myfile: file of Coeff; dd: Coeff;
function gorner1(const dd:Coeff): extended; var pp:extended; i:integer;
begin pp:=dd[n]; for i:=1 to n do pp:=pp*t+dd[n-i]; gorner1:=pp; end;
function gorner2(const dd:Coeff): extended; var pp:extended;i:integer;
begin pp:=dd[n]*n/h; for i:=1 to n-1 do pp:=pp*t+dd[n-i]*(n-i)/h; gorner2:=pp; end;
begin AssignFile(myfile,FILEPATH); Reset(myfile);
if x<bb then rr:=trunc((x-aa)/hh) else rr:=trunc((x-aa)/hh)-1; seek(myfile,rr);
read(myfile,dd); t:=(x-(aa+rr*hh))/h; f:=gorner1(dd); proiz:=gorner2(dd); CloseFile(myfile); end;
begin
hh:=(bb-aa)/power(2,k);h:=hh/n; calc(xpr);
writeln(‘xpr=’,xpr,’; f(xpr)=’,f,’; pogr=’,abs(f-f_pr));
writeln(‘xpr=’,xpr,’; proiz(xpr)=’,proiz,’; pogr=’,abs(proiz-proiz_pr));
readln; end.
Результат работы программы:
xpr= 5.47619047619048E-0001; f(xpr)=1.62283728597858E+0000; pogr= 1.45463068673690E-0014
xpr= 5.47619047619048E-0001; proiz(xpr)=-2.83347006210879E+0000; pogr= 1.27473643619924E-0011
В результате значение гамма-функции в произольной точке отрезка [a, b] = [0.5, 1] воспроизводится с погрешностью порядка 10–14 за время 5(ty + tc), следом воспроизводится значение ее производной с погрешностью порядка 10–11 за время 4(ty + tc). В этих оценках не учитывается время обращения к соответственной строке типизированного файла.
Замечание 1. Согласно ходу эксперимента можно предположить, что точность воспроизведения гамма-функции и ее производной только что изложенным способом может быть существенно увеличена за счет роста числа подынтервалов без изменения времени последующего воспроизведения. Значения на любом другом промежутке могут вычисляться с использованием формулы Г(х + 1) = xГ(х) [6, с. 361]. Необходимо отметить, что способ обладает естественным параллелизмом, и значения во множестве точек могут вычисляться одновременно при наличии соответственного числа процессорных элементов параллельной вычислительной системы. Кроме того, очевидным параллелизмом по всем подынтервалам обладает и собственно метод априорного вычисления коэффициентов полинома, приближающего функцию. Непосредственно преобразования интерполяционного полинома к виду алгебраического полинома с числовыми коэффициентами также распараллеливаются [2].
Кусочно-интерполяционное воспроизведение решений ОДУ и функции Бесселя
Задачу Коши для системы ОДУ можно решить с помощью кусочно-интерполяционного метода, при этом приближение каждого компонента решения будет непрерывной и непрерывно дифференцируемой функцией на всем отрезке решения [4]. На каждом подынтервале приближение решения будет представлять собой интерполяционный полином Ньютона (или Лагранжа), преобразованный к виду алгебраического полинома с числовыми коэффициентами. Для простоты метод поясняется (это необходимо для дальнейшего) для одного уравнения с оговоркой относительно общего случая. Пусть рассматривается задача Коши
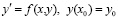, (20)
в области
,
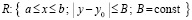где функция f(x,y) определена, непрерывно дифференцируема (в точках a – справа, b – слева) и удовлетворяет условию Липшица:
.
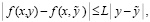
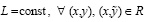Предполагается, что решение задачи (20) существует и единственно во всей области R. Пусть a, b те же, что в (6), и выполнено такое же разбиение на подынтервалы [ai , bi]. С целью интерполяции правой части (20) в f(x,y) подставляется приближенное значение y, вначале y ≈ y0. Функция f(x) = f(x,y0) приближается полиномами вида (15) (или (7)) по изложенной выше схеме. При фиксированных n и k на отрезке [ai, bi], при i = 0, затем, аналогично, при i = 1,2,… , выполняется следующее итерационное уточнение.
Пусть согласно (15)
,
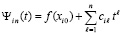тогда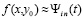 
, 
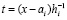, hi – шаг интерполяции на [ai, bi].
Первообразная, взятая в виде
,
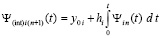или,
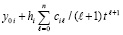
(на начальном подынтервале для произвольной постоянной полагается c00 = y00 = y0, на последующих подынтервалах выбор y0i поясняется ниже), принимается за приближение решения:
, 
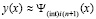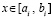
Тогда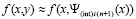 
, и при том же значении n, на том же подынтервале строится интерполяционный полином вида (15) для аналогичного приближения:
, 
.
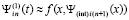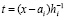От этого полинома снова берется первообразная с тем же значением константы
,
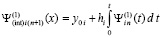подставляется в правую часть,
,
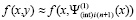которая затем аналогично интерполируется,
, 
.
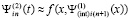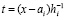Итерации
, 
,
, 
,
,
,
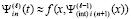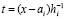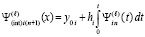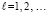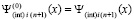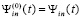продолжаются до априори заданной границы: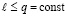 
.
Всюду выше предполагалось, что за значение y0i было взято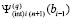 
. По окончании итераций на [ai, bi] выполняется переход к 
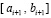, где за значение 
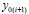принимается 
.
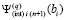Таким образом,
.
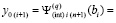
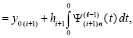
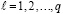Отсюда
, 
,
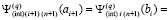
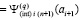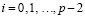и интегральные полиномы совпадают на каждой общей границе всех соседних подынтервалов. Тем самым кусочно-полиномиальное приближение решения является непрерывной функцией на всем [a, b] из (6).
Кусочно-полиномиальное приближение производной от решения также является непрерывной функцией на всем [a, b].
В самом деле,
, 
,
.
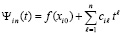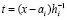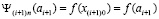С другой стороны, по построению,
,
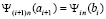то есть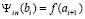 
.
В результате полиномы на всех соседних подынтервалах имеют одинаковое значение на общей границе.
С учетом того, что полиномы Лагранжа и Ньютона равной степени совпадают при равном числе, одинаковом расположении узлов интерполяции и одинаковых значениях в узлах интерполяции [1], полином Ψin(t) приближает правую часть (20) с оценкой абсолютной погрешности (11). Отсюда вытекает равномерная сходимость Ψin(t) именно к производной решения задачи (20). Чтобы это показать формально, можно воспользоваться следующими утверждениями из [3, 4].
Лемма 1 [4]. Пусть для произвольного n = const функция y = f(x) определена, непрерывна и непрерывно дифференцируема n + 1 раз на отрезке [a, b], на концах которого подразумеваются соответственные односторонние производные. Тогда, каково бы ни было n ≥ 1, последовательность полиномов Ψin(t) из (15) равномерно сходится к функции f(x) на данном отрезке при k→∞, где предполагается, что k = log2p, p – число подынтервалов из (6). Скорость сходимости оценивается из (11) при замене Pin(t) на Ψin(t), где c = const,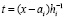 
, 
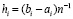, h – шаг интерполяции полинома Ψin(t) на [a, b] при k = 0: 
.
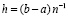В случае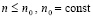 
, имеет место
Следствие 1 [4]. В условиях леммы 1, в предположении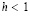 
, для любого i из (6) выполняется неравенство
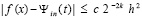, (21)
где c = const не зависит от выбора степени полинома n.
Замечание 2. В условиях следствия 1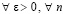 
: 
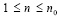, для всех i из (6) согласно (21) 
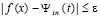, лишь только 
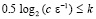, где предполагается, что k = log2p.
Равномерная сходимость на [a, b] полиномов Ψin(t) из (15), независимо от порядка гладкости функции f(x), начиная с двукратной непрерывной дифференцируемости, относится только к функции f(x) из леммы 1. Эти утверждения нельзя непосредственно отнести к правой части f(x,y) из (20). Рассуждения, доказывающие лемму и следствие [4], можно повторить для рассматриваемого приближения функции правой части (20). Тогда эти утверждения сохранятся, если в них функцию f(x) заменить функцией
.
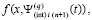
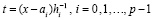В результате полиномы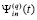 
будут равномерно сходиться не к f(x,y) из (20), а к кусочно-полиномиальному (кусочно-интерполяционному) приближению правой части (20)
.
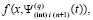
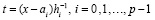Далее, относительно рассматриваемого метода решения задачи (20) в [3] приводятся следующие утверждения.
Лемма 2 [3]. Пусть выполнены условия леммы 1 применительно к правой части (20), а также условие
,
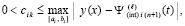
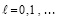где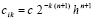 
из правой части (11). Пусть, кроме того, 
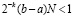, и выполняется кусочная интерполяция с итерационным уточнением решения задачи (20). Тогда на произвольном отрезке [ai, bi] из (6) найдется номер r0 , такой, что итерационное уточнение будет удовлетворять неравенству
.
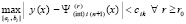Теорема 1 [3]. В условиях леммы 2 абсолютная погрешность решения задачи (20) оценивается из неравенства
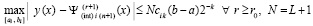, (22)
где L – константа Липшица. Согласно (22) погрешность кусочной интерполяции на любом подынтервале за счет итерационного уточнения уменьшается пропорционально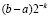 
.
Следствие 2 [3]. Из (22) следует оценка
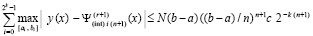. (23)
Пусть задано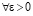 
. В (23) можно указать такое 
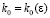, что правая часть не превзойдет ε при 
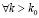. Именно, 
.
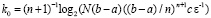С учетом неравенства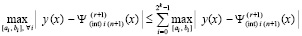 
имеет место
Теорема 2. В условиях леммы 2 абсолютная погрешность решения задачи (20) на всем отрезке решения из (6) оценивается из (23). При этом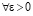 
верно соотношение
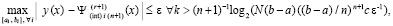(24)
,
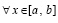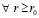, означающее равномерную сходимость метода, если k→∞.
Из изложенного вытекает
Теорема 3. В тех же условиях имеет место равномерная сходимость рассматриваемого приближения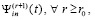 
к производной от решения, то есть к правой части (20).
Доказательство. С применением условия Липшица
.
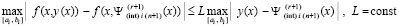Поэтому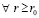 
выполнено
.
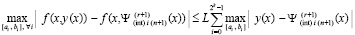Отсюда и из (24)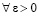 
.
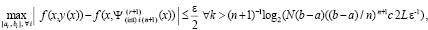
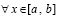Поскольку
,
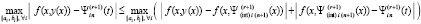то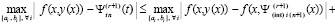 
.
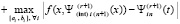
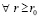Следовательно,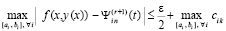 
,
где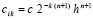 
из правой части (11).
В свою очередь,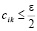 
, если 
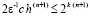, или, 
.
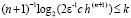Окончательно,
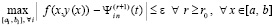
для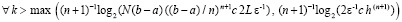 
.
Это означает равномерную сходимость полиномов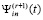 
к производной от решения задачи (20): 
, 
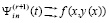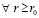, если k→∞. Теорема доказана.
Следствие 3. В силу
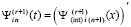
равномерное приближение производной решения получается из равномерного приближения решения полиномами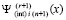 
путем взятия табличной производной от 
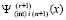в соответствии с (16).
В данном случае, согласно следствию, если интерполяционный полином приближает решение, то производная от него приближает производную от решения (в общем случае это утверждение не выполняется [1]). Обычно точность численного приближения производной ниже точности приближения функции [3], что видно и на приведенном примере приближения гамма-функции. Однако в излагаемом методе приближение решения получается из приближения производной, и точность приближения производной может оказаться либо близкой к приближению решения, либо выше точности приближения решения, как показывают приводимые ниже результаты экспериментов.
Замечание 3. Изложенный метод переносится на случай системы ОДУ повторением данных рассуждений на случай каждого уравнения системы в отдельности, аналогично переходу к системе, рассмотренному для данного метода в [4].
Если коэффициенты интерполирующего полинома Ψin(t) вида (15) на каждом подынтервале с номером i сохранять как i-ю строку массива или типизированного файла, то компоненты решения системы ОДУ с помощью адресации (9) за время (10) могут воспроизводиться произвольное число раз в произвольных точках всего отрезка решения без повторного решения системы. Такое воспроизведение обладает естественным параллелизмом и может одновременно выполняться во множестве точек для множества компонентов системы.
Непосредственно ниже предложенный метод иллюстрирует ОДУ, решением задачи Коши для которого является специальная функция.
Решение уравнения
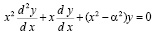(25)
на полуоси x > 0 при α ≥ 0 является функцией Бесселя первого рода Jα(x), которая для целочисленного значения α может быть представлена в виде
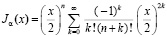[6].
Задача Коши для уравнения (25) может быть эквивалентно преобразована к виду задачи Коши для системы уравнений первого порядка
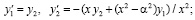
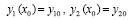. (26)
В качестве конкретного примера рассматривается кусочно-интерполяционное решение задачи (26) в случае α = 1 на отрезке [1, 2]. Приближенное решение выполняется с помощью программы VPI_J1, представленной ниже. Начальные значения для (26) взяты из базы знаний Wolfram|Alpha (J1(1) и 1/2(J0(1) - J2(1))) [7], – в программе Ynach1 и Ynach2.
program vpi_newton; {$APPTYPE CONSOLE} uses SysUtils;
const a0=1; b0=2; {границы отрезка приближения решения} FILEPATH1=’D:\y1.bin’; FILEPATH2=’D:\y2.bin’; {пути к файлам для хранения коэффициентов аппроксимирующих полиномов}
Ynach1=0.44005058574493351596; Ynach2=0.32514710081303303549; {начальные значения}
K_iter=30; {число итераций в процессе итерационного уточнения}
Nmin=3; Nmax=6; Kmin=0; Kmax=10; {границы для вариации степени полиномов и числа подынтервалов}
type Coeff = array[0..Nmax] of extended; var file1,file2: file of Coeff; dd1,dd2:Coeff;
function f1(x,y1,y2: extended):extended; begin f1:=y2 end;
function f2(x,y1,y2: extended):extended; var a:extended; begin a:=1; f2:=-(x*y2+(x*x-a*a)*y1)/(x*x); end;
procedure RD; type matr=array[0..Nmax,0..Nmax] of extended; vect=array[0..Nmax] of extended;
matrC=array[-5..Nmax] of extended; matrAll=array[0..33000] of matrC; matrC_=^matrAll;
var pod:longint; n,k:byte; i,j,ll:integer; x,y01,y02,a00,b00,max,min,MinGL,s,Min0,h,s1,s2,otrezok_integr:extended;
Ck11,Ck12,Ck1_,Ck1_opt,Ck21,Ck22,Ck2_,Ck2_opt:matrC_; d:matr;
procedure Viet(n:byte; var d:matr); var k,i:byte; e:matr; begin
e[1,1]:=1; e[1,0]:=0; for k:=2 to n do begin e[k,0]:=-e[k-1,0]*(k-1);
for i:=1 to k-1 do e[k,k-i]:=e[k-1,k-i-1]-e[k-1,k-i]*(k-1); e[k,k]:=e[k-1,k-1] end;
for k:=1 to n do for i:=0 to k do d[i,k]:=e[k,i] end;
procedure Konech_Raznoct(fy:vect; n:byte; var dy:matr); var i,j:byte; begin
for j:=0 to n-1 do dy[1,j]:=fy[j+1]-fy[j]; for i:=2 to n do for j:=0 to n-i do dy[i,j]:=dy[i-1,j+1]-dy[i-1,j] end;
procedure Newton(U:Vect; n:byte; var Mcoef:matrC); var dy:matr; b:vect; p,s:extended; j,i:byte;
begin Konech_Raznoct(U,n,dy); p:=1; for j:=1 to n do begin p:=p*j; b[j]:=dy[j,0]/p; end; Mcoef[0]:=U[0];
for i:=1 to n do begin s:=0; for j:=i to n do s:=s+d[i,j]*b[j]; Mcoef[i]:=s; end end;
function Gorner(Mcoef:matrC; x:extended):extended; var i,n:byte; s,t:extended;
begin t:=(x-Mcoef[-1])/Mcoef[-2]; n:=trunc(Mcoef[-3]); s:=Mcoef[n];
for i:=n-1 downto 0 do s:=t*s+Mcoef[i]; Gorner:=s end;
procedure Polynomial(x:vect; h,y01,y02:extended; n,k,K_iter:integer; var C1,C2:matrC);
var i,iter:integer; fy1,y1,fy2,y2:vect; A1,A2:matrC;
begin for i:=0 to n do y1[i]:=y01; for i:=0 to n do y2[i]:=y02;
for iter:=1 to K_iter do begin for i:=0 to n do begin fy1[i]:=f1(x[i],y1[i],y2[i]); fy2[i]:=f2(x[i],y1[i],y2[i]) end;
Newton(fy1,n,A1); Newton(fy2,n,A2);
C1[0]:=y1[0]; C1[-1]:=x[0]; C1[-2]:=h; C1[-3]:=n+1;C1[-4]:=k;C1[-5]:=n*h;
C2[0]:=y2[0]; C2[-1]:=x[0]; C2[-2]:=h; C2[-3]:=n+1;C2[-4]:=k;C2[-5]:=n*h;
for i:=1 to n+1 do begin C1[i]:=A1[i-1]*h/i; C2[i]:=A2[i-1]*h/i; end;
for i:=1 to n do begin y1[i]:=Gorner(C1,x[i]); y2[i]:=Gorner(C2,x[i]); end; end end;
procedure Subinterval(k,n,K_iter:integer; a0,b0,Ynach1,Ynach2:extended;var Ck1,Ck2:matrC_);
var hpd,a00,b00,y01,y02,h:extended; m,pod:longint; x:vect; j:byte;
begin hpd:=(b0-a0)/exp(k*ln(2)); a00:=a0; b00:=a00+hpd; y01:=Ynach1;y02:=Ynach2; x[0]:=a0; m:=0; pod:=0;
while a00<=b0-hpd/2 do begin h:=(b00-a00)/n; for j:=1 to n do begin inc(m); x[j]:=a0+m*h end;
Polynomial(x,h,y01,y02,n,k,K_iter,Ck1^[pod],Ck2^[pod]); y01:=Gorner(Ck1^[pod],x[n]);
y02:=Gorner(Ck2^[pod],x[n]); x[0]:=x[n]; inc(pod); a00:=a00+hpd; b00:=a00+hpd end end;
function Integral(a0,b0,a00,b00:extended; Ck:matrC_):extended; var pod1,pod2,m:longint; x1,x2,h,ss:extended;
begin h:=(b00-a00)/5; m:=0;x1:=a00;x2:=a00+h;ss:=0; repeat pod1:=trunc((x1-a0)/Ck^[0,-5]);
if abs(x2-b0)<1e-15 then pod2:=trunc(exp(Ck^[0,-4]*ln(2)))-1 else pod2:=trunc((x2-a0)/Ck^[0,-5]);
ss:=ss+abs(Gorner(Ck^[pod2],x2)-Gorner(Ck^[pod1],x1));
inc(m); x1:=a00+m*h;x2:=x1+h; until x2>b00+h/2; Integral:=ss; end;
begin Viet(Nmax,d); New(Ck11);New(Ck12);New(Ck1_);New(Ck1_opt); New(Ck21); New(Ck22);
New(Ck2_);New(Ck2_opt); MinGL:=1.18E32; n:=Nmin-1;
repeat k:=Kmin; Min:=1.18E32; repeat Subinterval(k,n,K_iter,a0,b0,Ynach1,Ynach2,Ck11,Ck21);
Subinterval(k+1,n,K_iter,a0,b0,Ynach1,Ynach2,Ck12,Ck22);
otrezok_integr:=sqrt(sqrt(abs(b0-a0))); max:=0; a00:=a0; b00:=a00+otrezok_integr; i:=0;
while b00<=b0 do begin s1:=abs(Integral(a0,b0,a00,b00,Ck12)-Integral(a0,b0,a00,b00,Ck11));
s2:=abs(Integral(a0,b0,a00,b00,Ck22)-Integral(a0,b0,a00,b00,Ck21));
if s1>s2 then s:=s1 else s:=s2; if s>max then max:=s;
inc(i); a00:=a0+i*otrezok_integr; b00:=a00+otrezok_integr; end;
if max<Min then begin Min:=max; Ck1_^:=Ck12^;Ck2_^:=Ck22^; end; inc(k);
until k>Kmax-1; if Min<MinGL then begin MinGL:=Min;
Ck1_opt^:=Ck1_^;Ck2_opt^:=Ck2_^; end; inc(n); until n>Nmax-1;
writeln(‘N=’,(Ck1_opt^[0,-3]):3:0,’ K=’,Ck1_opt^[0,-4]:3:0); {вывод на экран программно определенных значений степени полиномов и числа подынтервалов приближения}
pod:=trunc(exp(trunc(Ck1_opt^[0,-4])*ln(2)))-1; AssignFile(file1,FILEPATH1); AssignFile(file2,FILEPATH2);
Rewrite(file1); Rewrite(file2); for i:=0 to pod do begin for ll := 0 to trunc(Ck1_opt^[0,-3]) do begin
dd1[ll]:=Ck1_opt^[i,ll]; dd2[ll]:=Ck2_opt^[i,ll]; end; for ll := trunc(Ck1_opt^[0,-3])+1 to Nmax do begin
dd1[ll]:=0; dd2[ll]:=0; end; writeln(‘ n_pod=’,i); for ll:= 0 to trunc(Ck1_opt^[0,-3]) do writeln(‘c1[‘,ll,’]=’,dd1[ll],’; c2[‘,ll,’]=’,dd2[ll]); write(file1,dd1); write(file2,dd2); end; {вывод на экран и запись в файлы коэффициентов полиномов, аппроксимирующих компоненты решения задачи Коши}
CloseFile(file1); CloseFile(file2); Dispose(Ck11); Dispose(Ck12); Dispose(Ck1_); Dispose(Ck1_opt);
Dispose(Ck21);Dispose(Ck22); Dispose(Ck2_); Dispose(Ck2_opt); end;
begin RD; readln; end.
Результат работы программы:
N = 6 K = 8
n_pod=0
c1[0]= 4.40050585744934E-0001; c2[0]= 3.25147100813033E-0001
c1[1]= 2.54021172510182E-0004; c2[1]=-2.54021172510182E-0004
c1[2]=-9.92270205117900E-0008; c2[2]=-7.01315215648807E-0008
c1[3]=-1.82634170740876E-0011; c2[3]= 2.13729284469057E-0011
c1[4]= 4.17440004516463E-0015; c2[4]= 2.88286219759756E-0015
c1[5]= 4.50455121258192E-0019; c2[5]=-5.68154407978716E-0019
c1[6]=-7.45565458781129E-0023; c2[6]=-5.04690464405687E-0023
n_pod=1
c1[0]= 4.41318208651655E-0001; c2[0]= 3.23875244335859E-0001
c1[1]= 2.53027534637390E-0004; c2[1]=-2.54720883316543E-0004
c1[2]=-9.95003450455246E-0008; c2[2]=-6.98104959195136E-0008
c1[3]=-1.81798166456106E-0011; c2[3]= 2.14304435261119E-0011
c1[4]= 4.18563346052092E-0015; c2[4]= 2.86863944238709E-0015
c1[5]= 4.48232542097636E-0019; c2[5]=-5.69666714719959E-0019
c1[6]=-7.47330110754575E-0023; c2[6]=-4.98808291160866E-0023
…………………………………………………………………………
n_pod=254
c1[0]= 5.77216268940375E-0001; c2[0]=-6.13415536834909E-0002
c1[1]=-4.79230888152273E-0005; c2[1]=-3.13271196478513E-0004
c1[2]=-1.22371561124419E-0007; c2[2]= 2.61539113167236E-0008
c1[3]= 6.81091440537376E-0012; c2[3]= 2.55335057340332E-0011
c1[4]= 4.98701284847115E-0015; c2[4]=-1.34958535116744E-0015
c1[5]=-2.10874388814525E-0019; c2[5]=-6.65800719068586E-0019
c1[6]=-8.65708847306609E-0023; c2[6]= 2.72638729897478E-0023
n_pod=255
c1[0]= 5.76973595061751E-0001; c2[0]=-6.29072526272579E-0002
c1[1]=-4.91462911150452E-0005; c2[1]=-3.13007743029289E-0004
c1[2]=-1.22268649620816E-0007; c2[2]= 2.65367106329359E-0008
c1[3]= 6.91060172730020E-0012; c2[3]= 2.55063476449395E-0011
c1[4]= 4.98170853663556E-0015; c2[4]=-1.36622023563020E-0015
c1[5]=-2.13474140276255E-0019; c2[5]=-6.64986508648038E-0019
c1[6]=-8.64238303995403E-0023; c2[6]= 2.65580122003692E-0023
В представленной программе реализован алгоритм «автоматического» выбора наименьшей степени полинома и наименьшего числа подынтервалов (для приближения решения) в заданных ограничениях. Алгоритм подробно описан в [4]. В границах вариации степени полиномов от n = 3 до n = 6 и числа подынтервалов – от p = 20 до p = 210 программно определились значения n = 6, p = 28, соответствующие приближению решения задачи (26) с минимальной погрешностью. Рассчитанные программой коэффициенты полиномиальных приближений для рассматриваемой функции Бесселя (y1 из (26)) и ее производной (y2 из (26)) сохраняются в типизированные файлы. После этого значения функции Бесселя первого рода единичного порядка J1(x) (α = 1) и ее первых двух производных на отрезке [1, 2] могут воспроизводиться произвольное число раз с погрешностью порядка 10–19 в любой точке отрезка приближения с применением следующей программы:
program calc_fun_deriv; {$APPTYPE CONSOLE} uses SysUtils, Math;
const nmax=6; aa=1; bb=2; n=6; k=8; {параметры приближения решения}
FILEPATH1=’D:\y1.bin’; FILEPATH2=’D:\y2.bin’; {пути к файлам, хранящим значения коэффициентов, аппроксимирующих решение полиномов}
xpr=1.5+1/21; f_pr = 0.5641385068083141846631 ; proiz_pr = 0.120587690235184972092;
proiz2_pr = -0.406520534815932824205; {проверочная точка и точные значения функции и ее первых двух производных в данной точке для вычисления абсолютной погрешности приближения}
var t,hh,h:extended; f,proiz,proiz2:extended; rr:integer;
procedure calc(x: extended); type Coeff = array[0..Nmax] of extended; var file1, file2: file of Coeff; dd1,dd2: Coeff;
function gorner1 (const dd:Coeff): extended; var pp:extended;i:integer;
begin pp:=dd[n]; for i:=1 to n do pp:=pp*t+dd[n-i]; gorner1:=pp; end;
function gorner2 (const dd:Coeff): extended; var pp:extended;i:integer;
begin pp:=dd[n]*n/h; for i:=1 to n-1 do pp:=pp*t+dd[n-i]*(n-i)/h; gorner2:=pp; end;
begin AssignFile(file1, FILEPATH1); Reset(file1); AssignFile(file2,FILEPATH2); Reset(file2);
if x<bb then rr:=trunc((x-aa)/hh) else rr:=trunc((x-aa)/hh)-1;
seek(file1,rr); read(file1,dd1); seek(file2,rr); read(file2,dd2); t:=(x-(aa+rr*hh))/h;
f:=gorner1(dd1); proiz:= gorner2(dd1); proiz2:= gorner2(dd2); CloseFile(file1);CloseFile(file2);end;
begin hh:=(bb-aa)/power(2,k); h:=hh/(n-1); calc(xpr);
writeln(‘xpr=’,xpr,’; f(xpr)=’,f,’; pogr=’,abs(f-f_pr));
writeln(‘xpr=’,xpr,’; proiz(xpr)=’,proiz,’; pogr=’,abs(proiz-proiz_pr));
writeln(‘xpr=’,xpr,’; proiz2(xpr)=’,proiz2,’; pogr=’,abs(proiz2-proiz2_pr)); readln; end.
Результат работы программы:
xpr= 1.54761904761905E+0000; f(xpr)= 5.64138506808314E-0001; pogr= 5.42101086242752E-0020
xpr= 1.54761904761905E+0000; proiz(xpr)= 1.20587690235185E-0001; pogr= 9.48676900924816E-0020
xpr= 1.54761904761905E+0000; proiz2(xpr)=-4.06520534815933E-0001; pogr= 1.08420217248550E-0019
Время вычисления приближенного значения функции 6(ty + tc), ее первой производной – 5(ty + tc), второй производной – 4(ty + tc). Для дополнительного сокращения времени вычисления можно построить кусочно-интерполяционное приближение решения задачи (26) при фиксированных значениях параметров [3] (без их «автоматического» выбора) с использованием следующей программы.
program fpi_newton; {$APPTYPE CONSOLE} uses SysUtils;
const a0=1; b0=2; FILEPATH1=’D:\y1.bin’; FILEPATH2=’D:\y2.bin’; k_iter=30;
Ynach1=0.44005058574493351596; Ynach2=0.32514710081303303549;
n_fix=4; k_fix=12; {фиксированные значения параметров приближения решения}
type Coeff = array[0..n_fix] of extended; var file1,file2: file of Coeff; dd1,dd2:Coeff;
function f1(x,y1,y2: extended):extended; begin f1:=y2 end;
function f2(x,y1,y2: extended):extended; var a:extended; begin a:=1; f2:=-(x*y2+(x*x-a*a)*y1)/(x*x); end;
procedure RD; type matr=array[0..n_fix,0..n_fix] of extended;
vect=array[0..n_fix] of extended; matrC=array[-5..n_fix] of extended;
matrAll=array[0..33000] of matrC; matrC_=^matrAll; var pod:longint; n,k:byte; i,ll:integer;Ck1,Ck2:matrC_; d:matr;
procedure Viet(n:byte; var d:matr); var k,i:byte; e:matr; begin e[1,1]:=1; e[1,0]:=0; for k:=2 to n do begin
e[k,0]:=-e[k-1,0]*(k-1); for i:=1 to k-1 do e[k,k-i]:=e[k-1,k-i-1]-e[k-1,k-i]*(k-1); e[k,k]:=e[k-1,k-1] end;
for k:=1 to n do for i:=0 to k do d[i,k]:=e[k,i] end;
procedure Konech_Raznoct(fy:vect; n:byte; var dy:matr); var i,j:byte; begin for j:=0 to n-1 do dy[1,j]:=fy[j+1]-fy[j];
for i:=2 to n do for j:=0 to n-i do dy[i,j]:=dy[i-1,j+1]-dy[i-1,j] end;
procedure Newton(U:Vect; n:byte; var Mcoef:matrC); var dy:matr; b:vect; p,s:extended; j,i:byte;
begin Konech_Raznoct(U,n,dy); p:=1; for j:=1 to n do begin p:=p*j; b[j]:=dy[j,0]/p; end; Mcoef[0]:=U[0];
for i:=1 to n do begin s:=0; for j:=i to n do s:=s+d[i,j]*b[j]; Mcoef[i]:=s; end end;
function Gorner(Mcoef:matrC; x:extended):extended; var i,n:byte; s,t:extended;
begin t:=(x-Mcoef[-1])/Mcoef[-2]; n:=trunc(Mcoef[-3]); s:=Mcoef[n];
for i:=n-1 downto 0 do s:=t*s+Mcoef[i]; Gorner:=s end;
procedure Polynomial(x:vect; h,y01,y02:extended; n,k,K_iter:integer; var C1,C2:matrC);
var i,iter:integer; fy1,y1,fy2,y2:vect; A1,A2:matrC;
begin for i:=0 to n do y1[i]:=y01; for i:=0 to n do y2[i]:=y02;
for iter:=1 to K_iter do begin for i:=0 to n do begin fy1[i]:=f1(x[i],y1[i],y2[i]); fy2[i]:=f2(x[i],y1[i],y2[i]) end;
Newton(fy1,n,A1); Newton(fy2,n,A2); C1[0]:=y1[0]; C1[-1]:=x[0]; C1[-2]:=h; C1[-3]:=n+1;C1[-4]:=k;C1[-5]:=n*h;
C2[0]:=y2[0]; C2[-1]:=x[0]; C2[-2]:=h; C2[-3]:=n+1;C2[-4]:=k;C2[-5]:=n*h;
for i:=1 to n+1 do begin C1[i]:=A1[i-1]*h/i; C2[i]:=A2[i-1]*h/i; end;
for i:=1 to n do begin y1[i]:=Gorner(C1,x[i]); y2[i]:=Gorner(C2,x[i]); end end end;
procedure Subinterval(k,n,K_iter:integer; a0,b0,Ynach1,Ynach2:extended;var Ck1,Ck2:matrC_);
var hpd,a00,b00,y01,y02,h:extended; m,pod:longint; x:vect; j:byte;
begin hpd:=(b0-a0)/exp(k*ln(2)); a00:=a0; b00:=a00+hpd; y01:=Ynach1;y02:=Ynach2; x[0]:=a0; m:=0; pod:=0;
while a00<=b0-hpd/2 do begin h:=(b00-a00)/n; for j:=1 to n do begin inc(m); x[j]:=a0+m*h end;
Polynomial(x,h,y01,y02,n,k,K_iter,Ck1^[pod],Ck2^[pod]); y01:=Gorner(Ck1^[pod],x[n]);
y02:=Gorner(Ck2^[pod],x[n]); x[0]:=x[n]; inc(pod); a00:=a00+hpd; b00:=a00+hpd end end;
begin Viet(n_fix,d); New(Ck1);New(Ck2); n:=n_fix-1; k:=k_fix;
Subinterval(k,n,K_iter,a0,b0,Ynach1,Ynach2,Ck1,Ck2); pod:=trunc(exp(k*ln(2)))-1;
AssignFile(file1,FILEPATH1); AssignFile(file2,FILEPATH2); Rewrite(file1); Rewrite(file2);
for i:=0 to pod do begin for ll := 0 to trunc(Ck1^[0,-3]) do begin dd1[ll]:=Ck1^[i,ll];dd2[ll]:=Ck2^[i,ll]; end;
write(file1,dd1); write(file2,dd2);writeln(‘ n_pod=’,i);
for ll:= 0 to trunc(Ck1^[0,-3]) do writeln(‘c1[‘,ll,’]=’,dd1[ll],’; c2[‘,ll,’]=’,dd2[ll]); end;
CloseFile(file1); CloseFile(file2); Dispose(Ck1);Dispose(Ck2); end;
begin RD; readln;end.
При значениях n = 4, p = 212 кусочно-интерполяционное приближение решения задачи (26) на отрезке [1, 2] после сохранения коэффициентов полиномиальных приближений позволяет вычислять значения функции Бесселя и ее первых двух производных с погрешностью порядка 10–19 за время 4(ty + tc), 3(ty + tc) и 2(ty + tc) соответственно с применением представленной выше программы newton_bessel. С этой целью в программе newton_bessel необходимо выполнить следующие изменения: заменить значения параметров приближения с n = 6; k = 8; на n = 4; k = 12; и значения адресов обращения к типизированным файлам, хранящим коэффициенты аппроксимирующих полиномов, заменить с FILEPATH1=’E:\bessel.bin’; FILEPATH2=’E:\bessel_deriv.bin’; на FILEPATH1=’E:\bessel_fix.bin’; FILEPATH2=’E:\bessel_deriv_fix.bin’. Результат работы программы newton_bessel после выполнения указанных изменений:
xpr= 1.54761904761905E+0000; f(xpr)= 5.64138506808314E-0001; pogr= 8.13151629364128E-0019
xpr= 1.54761904761905E+0000; proiz(xpr)= 1.20587690235185E-0001; pogr= 4.20128341838133E-0019
xpr= 1.54761904761905E+0000; proiz2(xpr)=-4.06520534815933E-0001; pogr= 5.14996031930615E-0019
Кусочно-интерполяционное воспроизведение гипергеометрической функции
Многие специальные и элементарные функции при определенных значениях параметров и преобразовании независимого аргумента могут быть получены из гипергеометрической функции y = F(a,b,c,z), удовлетворяющей дифференциальному уравнению Гаусса (гипергеометрическому дифференциальному уравнению [6])
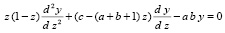, (27)
где a, b, c могут быть произвольными комплексными числами. В качестве конкретного примера рассматривается уравнение (27) при a = 1, b = 1, c = 2, z = –x. Задача Коши для уравнения (27) при данных значениях параметров может быть эквивалентно преобразована к виду задачи Коши для системы уравнений первого порядка
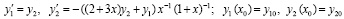. (28)
Первый компонент решения задачи (28),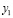 
, определяет гипергеометрическую функцию F(1,1,2,–x), через которую выражается суперпозиция элементарных функций 
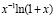. Кусочно-интерполяционное приближение решения задачи (28) строится на отрезке [1, 2] при начальных значениях: 
, 
.
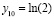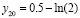Для решения данной задачи с помощью представленной выше программы vpi_newton с автоматическим выбором параметров приближения в ней необходимо задать соответствующие величины констант для начальных условий: Ynach1=0.693147180559945309417; Ynach2=-0.193147180559945309417; и подпрограмму для вычисления второго компонента функции правой части системы (28): function f2(x,y1,y2: extended):extended; begin f2:=(y1+(2+3*x)*y2)/(-x*(1+x)); end; Результат работы программы vpi_newton после выполнения указанных изменений:
N = 5 K = 10
n_pod=0
c1[0]= 6.93147180559945E-0001; c2[0]=-1.93147180559945E-0001
c1[1]=-4.71550733788929E-0005; c2[1]= 3.32749905077858E-0005
c1[2]= 4.06188848971991E-0009; c2[2]=-4.73508487223590E-0009
c1[3]=-3.85342193333389E-0013; c2[3]= 6.31874071599231E-0013
c1[4]= 3.85665096872492E-0017; c2[4]=-8.18102889871224E-0017
c1[5]=-3.98949209434325E-0021; c2[5]= 1.03993146610166E-0020
n_pod=1
c1[0]= 6.92958625231994E-0001; c2[0]=-1.93014156318853E-0001
c1[1]=-4.71225967575325E-0005; c2[1]= 3.32371401378332E-0005
c1[2]= 4.05726808323156E-0009; c2[2]=-4.72751023050888E-0009
c1[3]=-3.84725767410964E-0013; c2[3]= 6.30566770603659E-0013
c1[4]= 3.84867181220694E-0017; c2[4]=-8.16022974550916E-0017
c1[5]=-3.97931777280885E-0021; c2[5]= 1.03679920884879E-0020
…………………………………………………………………………...
n_pod=1023
c1[0]= 5.49411624815614E-0001; c2[0]=-1.08037627350261E-0001
c1[1]=-2.63763738648099E-0005; c2[1]= 1.28104262689107E-0005
c1[2]= 1.56377273790414E-0009; c2[2]=-1.24139691783414E-0009
c1[3]=-1.01025139793880E-0013; c2[3]= 1.12161351649742E-0013
c1[4]= 6.84578362795783E-0018; c2[4]=-9.79722426540246E-0018
c1[5]=-4.77944957933139E-0022; c2[5]= 8.38637064036887E-0022
После расчета и сохранения в типизированном файле коэффициентов полиномиальных приближений решения задачи (28) гипергеометрическая функция F(1,1,2,–x) и ее первые две производные на отрезке [1, 2] могут воспроизводиться произвольное число раз с погрешностью, не превышающей порядка 10–19, в любой точке отрезка приближения с применением программы calc_fun_deriv, в которой необходимо заменить значения параметров приближения с n = 6; k = 8; на n = 5; k = 10 и задать точные значения функции F(1,1,2,–x) и ее первых двух производных в проверочной точке xpr = 1.5+1/21: f_pr = 0.604256724299978314311; proiz_pr = -0.136812324802890373043; proiz2_pr = 0.077247729744803399694;
Результат работы программы:
xpr= 1.54761904761905E+0000; f(xpr)= 6.04256724299978E-0001; pogr= 7.04731412115578E-0019
xpr= 1.54761904761905E+0000; proiz(xpr)=-1.36812324802890E-0001; pogr= 2.71050543121376E-0020
xpr= 1.54761904761905E+0000; proiz2(xpr)= 7.72477297448034E-0002; pogr= 1.35525271560688E-0019
Время вычисления приближенного значения гипергеометрической функции 5(ty + tc), ее первой производной – 4(ty + tc), второй производной – 3(ty + tc). С целью дополнительного снижения времени вычисления, аналогично тому, как было показано для приближения функции Бесселя, строится кусочно-интерполяционное приближение решения задачи (28) при фиксированных значениях параметров с использованием программы fpi_newton. После задания соответствующих констант для начальных условий и подпрограммы для вычисления второго компонента функции правой части системы (28), программа fpi_newton формирует файлы с коэффициентами полиномиальных приближений решения задачи (28). Далее, в calc_fun_deriv задаются требуемые значения параметров: nmax = 4; n = 4; k = 12. Результат работы программы calc_fun_deriv:
xpr= 1.54761904761905E+0000; f(xpr)= 6.04256724299978E-0001; pogr= 8.13151629364128E-0019
xpr= 1.54761904761905E+0000; proiz(xpr)=-1.36812324802890E-0001; pogr= 9.48676900924816E-0020
xpr= 1.54761904761905E+0000; proiz2(xpr)= 7.72477297448034E-0002; pogr= 4.33680868994202E-0019
В этом случае значения гипергеометрической функции и ее первых двух производных вычисляются с абсолютной погрешностью порядка 10–19 за время 4(ty + tc), 3(ty + tc) и 2(ty + tc) соответственно.
О значении непрерывных кусочно-полиномиальных приближений с запоминаемыми коэффициентами
Относительно приближения функций рассмотренным методом необходимо отметить следующее. Во-первых, на данной основе сравнительно просто создается библиотека стандартных и часто повторяющихся функций. При этом для произвольно заданной точности приближения достигается минимальное время вычисления (за счет уменьшения длины подынтервалов при одновременном увеличении их количества и фиксировании степени полинома). В силу общности понятия интерполяции библиотека охватывает широкий класс функций в произвольном диапазоне изменения аргумента в области допустимых значений. Во-вторых, при приближении функций, задаваемых сложным алгоритмом, могут возникать принципиальные трудности для исследования этих функций. В то же время кусочно-полиномиальное приближение этих функций со свойством непрерывности дает возможность выполнить искомое исследование как исследование данного приближения. При этом все экстремумы и нули функции можно идентифицировать программно («автоматически»), подав данное непрерывное приближение на вход программы, основанной на устойчивой адресной сортировке [8].
Относительно приближения решения задачи Коши для системы ОДУ рассмотренным методом принимается во внимание следующее. Во-первых, непрерывное кусочно-полиномиальное приближение к решению становится хранимым без ограничения во времени: в типизированных файлах хранятся коэффициенты полиномов покомпонентного приближения в соответствии каждому подынтервалу. Область приближенного решения практически может быть произвольной, но ограниченной. То же относится к непрерывному кусочно-полиномиальному приближению компонентов производной от решения (правой части системы). Хранимое приближение решения может воспроизводиться неограниченное число раз в произвольном множестве точек приближения. При этом время восстановления приближения решения (производной) в любой точке измеряется согласно (10) с использованием адреса (9) для строки типизированного файла, и не требуется последовательное прохождение всех точек решения заново. Этот процесс обладает естественным параллелизмом, приближение решения и производной может восстанавливаться одновременно во всем требуемом множестве точек, но при необходимости может воспроизводиться последовательно без трудоемкой обработки правой части системы. Такое качество приближения целесообразно для исследования и ускорения численных дифференциальных моделей процессов. Во-вторых, факт получения, хранения и возможности воспроизведения непрерывного и непрерывно дифференцируемого кусочно-полиномиального приближения решения задачи Коши для системы ОДУ предоставляет возможность математического исследования особенностей решения и производной. В силу аналитичности приближений применимыми оказываются все известные математические методы, но процесс исследования можно «автоматизировать», подавая хранимое приближение на вход отмечавшейся программы на основе сортировки [8].
Непосредственно само приближенное решение, получаемое методом кусочной интерполяцией с итерационным уточнением (с «автоматическим» выбором степени полинома и числа подынтервалов), отличается качеством существенно ограниченного накопления погрешности по длине промежутка решения [4]. Это означает, что хранимое приближение будет обладать высокой точностью (и одновременно высокой скоростью воспроизведения) на всем промежутке решения. Время последовательного воспроизведения хранимого приближения решения (и производной) на всем промежутке приближения измеряется произведением степени полинома на количество подынтервалов: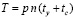 
, где p из (6). Оценка указывает на отсутствие обращений к правой части системы, которые обычно определяют трудоемкость приближенного метода, но при воспроизведении хранимого приближения такие обращения исключены по построению. Существенна та особенность хранимого приближения, что воспроизводить его можно в любом порядке: не обязательно от начальной точки к конечной. В частности, воспроизводить приближение можно от конца к началу, от середины промежутка к началу и к концу. То же можно делать отдельно по любым частям промежутка и т.д. Формально воспроизведение приближения взаимно независимо по всем частям промежутка приближения, причем значения данных являются готовыми во всех частях. Это влечет максимальный параллелизм воспроизведения хранимого приближения (с разбиением (6) на независимые части), что ускоряет и без того быстрый процесс пропорционально числу R процессорных элементов параллельной вычислительной системы: 
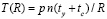. В частности, если R = p, то 
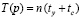, и решение воспроизводится за время вычисления полинома по схеме Горнера. Само вычисление полинома можно ускорить с помощью известных схем распараллеливания, тогда, в частности, может быть достигнуто время воспроизведения хранимого приближения решения с оценкой 
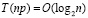. Если же n мало и фиксировано, то 
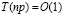. Это существенно отличает предложенный метод от классических [9, 10] и современных [11, 12] методов численного интегрирования ОДУ.
Необходимо оговориться, что допустимое в оценках сложности абстрагирование от обмена в данном случае может оказаться некорректным. Нельзя рассматривать одновременное обращение к памяти многих процессорных элементов, не указав архитектуру памяти вычислительной системы, поскольку вся суть воспроизведения приближения завязана на структуру типизированного файла. Тем не менее просматривается возможность распределить такой файл по секторам памяти с доступом для каждого процессорного элемента.
В-третьих, все качества быстродействия и точности хранимых приближений могут быть задействованы еще на этапе априорного решения задачи Коши для системы. Именно, для всех функций правых частей системы может быть создана библиотека стандартных программ рассмотренного выше вида. Тогда при первоначальном приближенном решении каждое обращение к правой части системы упрощается и ускоряется. Можно объединить рассмотренные свойства для определения в навигационном приемнике текущих значений координат и составляющих вектора скорости центра масс навигационного космического аппарата (НКА). Тогда окажется, что на заданный момент времени из 30-минутного интервала прогнозирования, рассчитываемого по оперативной эфемеридной информации из навигационного сообщения на основе численного интегрирования дифференциальных уравнений движения центра масс НКА [13], искомые координаты могут быть получены с повышенной точностью, затем многократно обработаны с целью уточненного предсказания. Для данного применения перспективной является возможность максимально параллельной обработки вычислений. Подобный подход с целью высокоточной быстродействующей обработки применяется в программе ORBGEN в составе Bernese GNSS высокоточного программного обеспечения для постобработки наблюдений глобальных навигационных спутниковых систем (ГНСС). Именно, реализовано хранение приближенного решения уравнений движения спутников в виде файла с коэффициентами полиномов, аппроксимирующих решение [14], однако метод аппроксимации отличается от кусочной интерполяции. Построение коэффициентов полиномов, аппроксимирующих решение уравнений движения спутников, в программе выполняется на основе метода коллокации, фактически являющегося неявным методом Рунге – Кутты [10], при этом точность исходного приближения понижается.
Из других возможностей предложенного метода отмечается возможность организации на его основе банка хранимых кусочно-полиномиальных приближений решений задачи Коши для одной системы при различных начальных значениях, а также аналогичных приближений для класса задач, что может использоваться при численном решении двухточечной задачи Коши [15] и для компьютерной оценки отклонения от невозмущенного решения.
Заключение
Изложен метод компьютерного вычисления функций, инвариантный относительно вида функции, точности приближения и временной сложности. Метод состоит в построении непрерывного кусочно-интерполяционного приближения функции одной действительной переменной, осуществляет аналогичное приближение решения задачи Коши для ОДУ и производной от решения. Приближение является хранимым в памяти компьютера, быстро воспроизводится и позволяет выполнять исследование функций, решения задачи Коши, производной от решения. Предложенное приближение характеризуется сравнительно высокой точностью и восстанавливается с малой временной сложностью. Раскрыта методика построения, показано математическое и техническое значение хранимой непрерывной кусочной интерполяции функий одной действительной переменной и решений задачи Коши для ОДУ применительно к многократному воспроизведению.
Библиографическая ссылка
Ромм Я.Е., Джанунц Г.А. О ВОСПРОИЗВОДИМОСТИ ФУНКЦИЙ, ПРОИЗВОДНЫХ И РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ХРАНИМЫХ КОЭФФИЦИЕНТОВ КУСОЧНОЙ ИНТЕРПОЛЯЦИИ // Современные наукоемкие технологии. – 2023. – № 1. – С. 44-63;URL: https://top-technologies.ru/ru/article/view?id=39497 (дата обращения: 21.11.2024).