Формирование и развитие функциональной грамотности учащихся представляет собой одну из приоритетных задач современной российской школы. Ее решение непосредственно связано с реализацией ФГОС, нацеливающего на использование в образовательном процессе комплексного системно-деятельностного подхода. Сегодня российская школа должна не только давать обучающимся предметные знания, но и учить их применять эти знания в предметных областях, в конкретных жизненных ситуациях.
В процессе освоения математики у обучающихся вырабатываются умения высказывать обоснованные математические суждения, доказывать гипотезы с помощью математических методов, анализировать те или иные жизненные ситуации, выявлять проблемы, возникающие в окружающем мире, интерпретировать результаты исследований и др. Другими словами, математика является одной из естественных сред формирования и развития функциональной грамотности. Отечественные исследователи активно обсуждают вопросы, связанные с организацией процесса формирования функциональной грамотности.
И.Н. Власовой и М.А. Худяковой [1] выделены методические условия формирования функциональной грамотности при обучении математике, в частности условие системного включения в процесс обучения специальным заданиям.
Особенности проектирования заданий в системе формирования математической функциональной грамотности выделены О.В. Симоновой [2].
О.А. Рыдзе, К.А. Краснянская [3] исследуют вопросы преемственности в формировании математической функциональной грамотности учащихся начальной и основной школ.
Егупова М.В. [4] раскрывает ряд методических проблем, связанных с практико-ориентированным обучением математике в школе.
В работе О.В. Аксеновой и др. [5] представлены лабораторные работы по математике как вид занятий, используемых в качестве инструмента формирования и контроля функциональной математической грамотности обучающихся.
Л.О. Рослова в своей статье [6] констатирует, что методика формирования навыков у обучающихся должна быть переориентирована на обеспечение развития формируемых умений, на выстраивание связей между понятиями, изучаемыми в разное время.
Проведенный нами анализ литературы показал, что на сегодняшний день разработано достаточно большое количество методических материалов, содержащих практические задачи, направленные на формирование математической грамотности как составной части функциональной: банк заданий на сайте института стратегии развития образования РАО, учебное пособие Т.Ф. Сергеевой «Математика на каждый день» и др. Разработаны сборники эталонных заданий, включающие в себя стартовые задания, обучающие задания, итоговые задания. Но, несмотря на имеющиеся методические материалы, процесс формирования функциональной грамотности у обучающихся носит эпизодический характер, не выстроена система приращения умений (изменение уровня владением умением), которые входят в состав математической грамотности как составной части функциональной.
Функциональная грамотность является сложным образованием, включающим различные виды грамотности, в том числе читательскую, логическую, информационную, экономическую и другие. По нашему мнению, эффективное формирование функциональной математической грамотности связано с повышением уровня логической грамотности обучающихся. В настоящей работе мы обратились к вопросу формирования и развития у обучающихся логической грамотности. При этом мы отмечаем особую роль в формировании математической грамотности умения рассуждать, которое пронизывает все виды деятельности, относящиеся к этому процессу (формулировать, применять, интерпретировать). В.А. Далингер отмечает, что умение рассуждать не приобретается спонтанно, его нужно целенаправленно развивать посредством специально подобранных задач [7]. Известно, что развитие логического мышления школьников происходит в процессе решения нестандартных задач на уроках математики и во внеурочной деятельности [8]. Решение нестандартных задач требует выработки повышенного внимания к анализу условия в сопоставлении с заключением, к построению взаимосвязанных цепочек логических рассуждений от данных к неизвестным и наоборот, высказыванию оценочных суждений в получении решений. К основным компонентам логической грамотности относятся: логические знания, логические действия, подвижность логических знаний и умений [9].
Цель исследования – поиск и методическое обоснование решения нестандартных заданий для начальной и основной школ, отвечающих условиям: 1) задания должны образовывать систему с разными уровнями проведения логических рассуждений; 2) задания должны реализовывать принцип преемственности при формировании математической грамотности; 3) задания могут быть использованы как на уроках, так и во внеурочной деятельности.
Материалы и методы исследования
Для проведения настоящего исследования использовались теоретические методы: сравнительно-сопоставительный анализ научно-методической литературы по проблеме формирования функциональной грамотности при изучении математики, анализ и обобщение педагогического опыта проектирования занятий, направленных на формирование математической функциональной грамотности учащихся основной школы на основе системно-деятельностного подхода [2, 5, 10]. Необходимый практический материал по заданиям авторов статьи разрабатывали и апробировали в период прохождения педагогической практики студенты 5 курса кафедры математики ЮУрГГПУ, обучающиеся по профилю «Математика. Информатика» в рамках дисциплины «Инновации в методике обучения математики». Серия заданий по приращению умения рассуждать создавалась в рамках проектной деятельности студентов под руководством авторов статьи. В процессе исследования авторы проводили обобщения полученных результатов в сопоставлении с собственным методическим опытом реализации принципа преемственности формирования умения рассуждать при обучении математике в основной школе.
Результаты исследования и их обсуждение
В современной начальной школе учителя используют технологии развивающего обучения, которые включают формирование и развитие логической грамотности обучающихся. Разработки отечественных исследователей легли в основу обновленных ФГОС, в систему УУД. Анализ научно-методической литературы и многолетнего опыта методической подготовки будущих учителей математики позволяет нам сделать вывод о том, что эффективность формирования математической грамотности возрастает при условии соблюдения принципа преемственности в формировании УУД, который отражается в обновленных ФГОС. Система УУД включает в себя познавательные действия, одной из составных частей которых является умение рассуждать, представляющее базовое логическое умение, обеспечивающее соблюдение принципа преемственности.
Если в начальной школе существенное внимание на уроках математики уделяется обучению построения рассуждений в форме связи простых суждений об объекте, то в основной школе больший акцент до сих пор остается на обучении основным математическим операциям. Обучающиеся выполняют осваиваемые действия «по трафарету», то есть неосознанно, без использования каких-либо рассуждений, без проговаривания заданий на естественном языке, что не способствует повышению их функциональной математической грамотности. Для устранения этого недостатка, по нашему мнению, в первую очередь надо обратить внимание на подготовку учителей, которые учат и воспитывают школьников. Это значит, что необходимо переориентировать методическую систему подготовки учителей математики основной школы на развитие умения рассуждать.
Наш курс «Инновации в методике обучения математики» построен с учетом возможности для будущих учителей принять участие в разработке системы заданий по формированию у обучающихся основной школы умения рассуждать с учетом принципа преемственности. Реализация принципа осуществлялась за счет учета навыков, полученных обучающимися в начальной школе, и включения в систему заданий с разными уровнями проведения логических рассуждений (логические задачи на простое воспроизведение, задачи на обобщенное воспроизведение, задачи на логический поиск решения) [9].
Приведем пример последовательности подобранных студентами задач, направленных на формирование у обучающихся начальной и основной школ умения рассуждать. Данную последовательность можно реализовать при изучении следующих тем: «Сложение и вычитание чисел», «Решение текстовых задач», «Логические задачи (логика и смекалка)» в 3–5 классах. Логическая простота заданий, связанных с числами, позволяет уже в начальной школе формировать навыки логических рассуждений на числовом материале. Выполняя несложные вычисления в задачах «на магические квадраты» (квадратные таблицы, заполненные натуральными числами, суммы которых по всем строкам, столбцам и обеим диагоналям одинаковы), учащиеся начальной школы знакомятся с методами организации полного перебора. В ходе решения этих задач в неявном виде проходит отработка навыков арифметических действий, а в явном − элементов логических операций (правила рассуждения, доказательство от противного) и установления соответствий при заполнении таблиц. Первые задания «на магические квадраты» порядка 3, с которыми сталкиваются ученики начальной школы – заполнить пустые клетки квадрата при известной сумме. Решение таких задач прямым перебором оказывается нерациональным. Знание суммы трех чисел и двух слагаемых из них (в каком-то столбце, строке или на диагонали) позволяет найти третий элемент. Вопросы учителя к учащимся: «Есть ли в квадрате строки, в которых заполнены 2 клетки? Есть ли столбцы, в которых заполнены 2 клетки? Есть ли диагонали, в которых заполнены 2 клетки? С заполнения какой клетки начнем заполнение квадрата?»
Система вопросов учителя помогает учащимся сконструировать алгоритм рассуждений, позволяющий прийти к ответу. Задача получает развитие, когда в ее условии сумма элементов не задается явно или увеличивается размер квадрата. Вопросы к учащимся: «Каким свойством должен обладать квадрат? Как узнать сумму чисел в строке? Каким способом можно заполнить квадрат?»
Мы предлагаем также рассматривать задачи на квадратные таблицы, где числа заменены буквами. В этом случае алгоритм решения задачи сохраняется, но при этом усложняется за счет дополнения новыми элементами. Использование в качестве дополнительной информации квадратов, полученных ранее, позволяет учащимся найти оригинальный способ решения с использованием поворота или отражения.
Увеличение размеров таблицы и уменьшение в процентном отношении числа известных данных усложняет логический анализ задачи.
Задача 1. (для 5 класса) Впиши в пустые клетки недостающие числа от 1 до 16 так, чтобы в сумме по всем столбцам, строкам и обеим диагоналям получалось одно и то же число.
В таких задачах сумму приходится искать по описанию самого квадрата: каждое число используется один раз, а сумма в каждом столбце равна частному от деления суммы всех элементов на число столбцов.
Если решение осложнено отсутствием столбца, строки или диагонали с одной пустой клеткой, то приходится определять «ключевую» («замковую») клетку и, анализируя одновременно несколько фактов о столбцах, строках и диагоналях с ее участием, подбирать ее содержимое. Отметим, что уровень логических рассуждений при последовательном выполнении заданий «на магические квадраты» повышается.
При решении математических задач часто возникают трудности в определении важности свойств объекта, влияющих на поиск решения. Часть используемых в рамках настоящего исследования заданий направлена на демонстрацию связей между средствами математики и языком, что помогает раскрыть возможности применения математических методов, в том числе и в лингвистике. В таких задачах обычно приводятся соответствующие друг другу конструкции на двух «языках», один из которых может быть даже не знаком решающим задачу школьникам. Требуется путем логического анализа установить закономерности и «перевести» (расшифровать) нужный текст.
К этому типу задач в начальной школе относятся примеры, связанные с переводом записи чисел в различных системах счисления (римской, арабской, египетской). Например: «Найди разность 1375 – XXXVII». Более сложной для обучающихся является задача для 4 класса «Найди значение выражения, где каждая буква обозначает цифру. (ПЫХПЫХПЫХПЫХ – ПЫХПЫХ): ПЫХПЫХ».
Эффективному решению таких задач помогут рассуждения обучающихся при анализе задания. Примерные вопросы учителя: «Видишь ли ты в задании числа? Как заданы числа? Сколько цифр в записи первого числа? Сколько различных цифр в записи выражения? Что надо сделать, чтобы перевести запись выражения на язык математики? Составьте аналогичную задачу и предложите товарищу ее решить».
Решение задач с необходимостью «расшифровки» их условий в начальной школе является подготовкой к решению других, более сложных задач такого типа в основной школе.
Задача 2. (для 5 класса) Известны некоторые словосочетания из древнекитайского языка (в их латинской транскрипции) и их переводы на русский язык:
rau bok gu − враг старого раба,
rau gu bok − раб старого врага,
gu rau bok − старый раб врага.
Учитывая, что в древнекитайском языке расположение слов в словосочетаниях происходит по обязательным правилам в определенном порядке, переведите на древнекитайский язык фразы: а) старый враг; б) раб врага.
Анализируя текст задачи (в том числе и на неизвестном языке), требуется найти закономерности, которые помогут путем рассуждений по наводящим вопросам учителя установить соответствия между элементами текста для составления словаря, а также выявить закономерности в конструировании фраз для правильного перевода.
В начальной школе используются задания на формулирование логических выводов на основе рассуждений при сравнении нескольких объектов. Например, для учащихся 2 класса предлагается задание «Сравни выражения: 0∙7, 0∙5, 0∙2, 0∙4. Чем они похожи? Чему равны значения этих произведений? Вычисли, заменив умножение сложением. Закончи фразу: При умножении числа 0 на натуральное число получится…». Учащимся четвертого класса можно предложить более сложную сюжетную задачу.
Задача 3. (для 4 класса). Аня, Боря, Вася и Галя ловили рыбу. Галя поймала больше, чем Вася. Аня и Боря вместе поймали рыбы столько же, сколько поймали Галя и Вася. Девочки вместе поймали меньше рыбы, чем мальчики. Как распределились между рыбаками места по количеству выловленной рыбы, если Боря поймал больше всех? Будет ли задача иметь решение, если предположить, что больше всех поймала Галя? Вася? Аня?
Решить задачу можно, применив при анализе условия моделирование на числовой прямой. Альтернативный способ – с помощью таблицы.
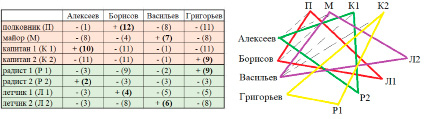
Иллюстрация решения задачи 4 с помощью таблицы и графа
В среднем звене усложнение заданий происходит чаще всего за счет логических связей между данными. Логические цепочки рассуждений удлиняются, появляются новые методы рассуждений и способы оформления решений. При решении задач с помощью таблиц, на основе анализа текста задачи требуется составить таблицу, описывающую связи между элементами двух или более множеств, и, заполнив ее, сделать нужный вывод. Освоение заданий описанных нами типов обеспечивает преемственность формирования у обучающихся навыков логических рассуждений на новом этапе.
Задача 4. (для 5 класса) Среди офицеров Алексеева, Борисова, Васильева и Григорьева – полковник, майор и два капитана. Известно, что звание Алексеева ниже, чем у Васильева. Алексеев и один из капитанов – радисты. Борисов и майор – летчики. Определите звание и род войск каждого из офицеров.
В ходе решения этой задачи обучающиеся часто сталкиваются с проблемами из-за неоднозначности условия. Приходится обсуждать ряд вопросов (как расположить полковника, майора и капитана по старшинству; если Алексеев и один из капитанов – радисты, то может ли Алексеев быть капитаном; и др.). Результаты логических рассуждений можно оформить в виде таблицы. Знаки «плюс» («минус») означают наличие (отсутствие) связи между элементами рассматриваемых множеств, а число в скобках − порядковый номер принятия решения. В качестве альтернативного способа решения можно рассмотреть использование графов (рисунок).
Разработанные серии заданий, опирающиеся на принцип преемственности обучения и нацеленные на приращение у обучающихся умения рассуждать, были апробированы студентами 5 курса в период прохождения педагогической практики в школах г. Челябинска на уроках математики и во внеурочной деятельности. Они обнаружили путем педагогического наблюдения появление у обучающихся четвертого и пятого классов положительной динамики в построении логических рассуждений после включения в процесс обучения разработанных заданий.
Заключение
На сегодняшний день разработано достаточно большое количество методических материалов, содержащих практические задачи, направленные на формирование математической грамотности как составной части функциональной, включающей формирование и развитие логических умений рассуждать, что позволяет выстраивать серии (системы) заданий с заданными требованиями к обучению на уроках математики и во внеурочной деятельности.
Серии сюжетных заданий, нацеленных на развитие умений проведения логических рассуждений, целесообразно использовать учителю в его практической деятельности по формированию математической грамотности обучающихся.
Учителей и будущих учителей математики необходимо специально готовить к разработке и использованию заданий, которые учитывают принцип преемственности в развитии умения рассуждать у учащихся начальной и основной школ.
Статья выполнена в рамках научно-исследовательской работы «Мониторинг формирования математической грамотности обучающихся основной школы», номер проекта МК-04-2022/68 от 28.04.2022.
Библиографическая ссылка
Севостьянова С.А., Мартынова Е.В. ПРЕЕМСТВЕННОСТЬ В ФОРМИРОВАНИИ ЛОГИЧЕСКОЙ ГРАМОТНОСТИ ОБУЧАЮЩИХСЯ НАЧАЛЬНОЙ И ОСНОВНОЙ ШКОЛ // Современные наукоемкие технологии. 2022. № 12-2. С. 377-382;URL: https://top-technologies.ru/ru/article/view?id=39488 (дата обращения: 03.02.2026).
DOI: https://doi.org/10.17513/snt.39488



