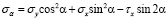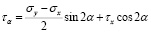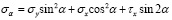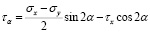Увеличение объема информации в науках и уменьшение времени на освоение учебного материала дисциплин, преподаваемых в вузах, стало объективной реальностью. Перед педагогической наукой стоит вопрос, как за короткий срок дать обучаемым максимально большое количество необходимой информации, как повысить результаты учебного труда. Ответы на эти вопросы дает совокупность педагогических приемов, позволяющих увеличить производительность учебного труда с одновременным повышением качества образования, называемая интенсификацией процесса обучения. В работах ученых выделен ряд факторов интенсификации обучения [1]. Такой фактор, как ускорение темпа учебных действий, имеет непосредственное отношение к написанию данной статьи. В учебной литературе по сопротивлению материалов даются задачи по определению касательных и нормальных напряжений в площадках, наклоненных к граням элементарного параллелепипеда. Формулы для определения этих напряжений даются только для одного положения площадки [2–4], хотя таких положений восемь. Для того чтобы решать задачи, студенту надо выводить эти формулы, что замедляет темп учебных действий. Здесь ставится другая задача – ускорить изучение темы «Напряженное и деформированное состояние в точке» и ускоренно применять знания на практике. С.П. Грушевский, А.А. Остапенко показали, что такие задачи решаются путем сгущения (уплотнения, сжатия, компрессии, концентрации) учебной информации [5].
Цель исследования – дать изучающим сопротивление материалов формулы для определения касательного и нормального напряжения в площадках, наклоненных к граням элементарного параллелепипеда, при плоском напряженном состоянии.
Материалы и методы исследования
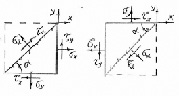
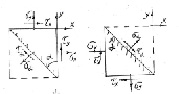
Для определения напряжений на любых площадках, проходящих через данную точку при плоском напряженном состоянии, будем рассматривать равновесие бесконечно малой (элементарной) треугольной призмы, образованной рассечением бесконечно малого (элементарного) параллелепипеда, построенного в окрестности рассматриваемой точки, плоскостью под углом α к боковым его граням, перпендикулярным плоскости чертежа. Высота призмы в направлении, перпендикулярном плоскости чертежа, равна dz. Основания призмы представляют собой прямоугольные треугольники (abc) с размерами dx, dy, ds, свободные от напряжений (рис. 1, а, б). Совместим систему координатных осей u, v с наклонной площадкой. Примем следующее правило знаков. Касательное напряжение по боковой грани положительно, если изображающий его вектор стремится вращать призму по часовой стрелке относительно любой точки, лежащей на внутренней нормали к этой грани, или внешнюю нормаль к грани необходимо поворачивать по часовой стрелке для совпадения с вектором касательного напряжения. Растягивающее напряжение положительно, а сжимающее – отрицательно. Угол α между площадкой, проходящей через рассматриваемую точку, и боковыми гранями элементарного параллелепипеда положителен, если грани надо поворачивать для совпадения с этой площадкой против часовой стрелки. Обозначим σx и τx напряжения, параллельные оси x, σy и τy – параллельные оси y, σα и τα – параллельные осям v и u соответственно. Напряжения σx, τx, σy, σα, τα возьмем положительными.
Задача 1. Определение касательных и нормальных напряжений на площадках, наклоненных к нижней грани элементарного параллелепипеда под углом α > 0 (рис. 1, а).
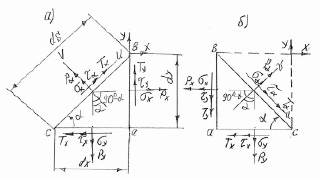
Рис. 1. Плоское напряженное состояние в точке: а) площадка bc наклонена к нижней грани ac под углом α > 0; б) площадка bc наклонена к нижней грани ac под углом α < 0
На гранях действуют сосредоточенные силы Px, Py, Tx, Ty, Pα, Tα, равные произведению соответствующего напряжения на площадь грани и приложенные в центрах тяжести этих граней:
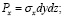
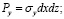
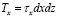
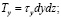
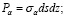
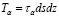 . (1)
. (1)
Призма находится в равновесии. Составим уравнения равновесия (приравниваем к нулю сумму проекций всех сил на оси u и v):
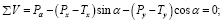 (2)
(2)
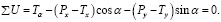 (3)
(3)
Подставим в уравнения (2) и (3) выражения сил из равенств (1):
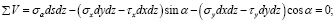
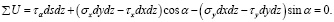
Сократив эти уравнения на dsdz, учитывая при этом, что (dy / ds) = sin α, а (dx / ds) = cos α будем иметь:
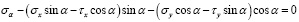 ; (4)
; (4)
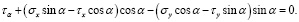 (5)
(5)
Раскрывая скобки и решая уравнения (4) и (5) относительно σα и τα, получаем
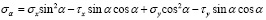 ; (6)
; (6)
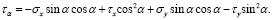 (7)
(7)
Заменяя τy на τх (они равны по модулю) в уравнениях (6) и (7), окончательно получаем
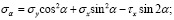 (8)
(8)
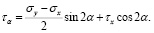 (9)
(9)
Задача 2. Определение касательных и нормальных напряжений на площадках, наклоненных к нижней грани элементарного параллелепипеда под углом α < 0 (рис. 1, б).
Призма находится в равновесии. Составим уравнения равновесия (приравниваем к нулю сумму проекций всех сил на оси u и v):
∑V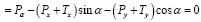 ; (10)
; (10)
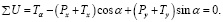 (11)
(11)
Подставим в уравнения (10) и (11) выражения сил из равенств (1):
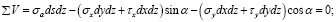
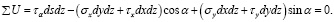
Сократив эти уравнения на dsdz, учитывая при этом, что (dy / ds) = sin α, а (dx / ds) = cos α, будем иметь
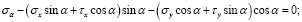
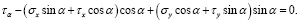
Раскрывая скобки и решая данные уравнения относительно σα и τα, получаем
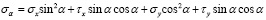 ;
;
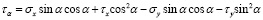 .
.
Заменяя τy на τх (они по модулю равны), окончательно будем иметь
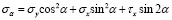 ; (12)
; (12)
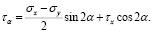 (13)
(13)
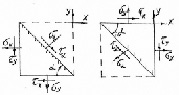
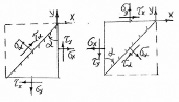
Задача 3. Определение касательных и нормальных напряжений на площадках, наклоненных к правой вертикальной грани элементарного параллелепипеда под углом α > 0 (рис. 2, а).
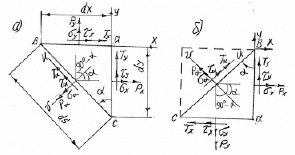
Рис. 2. Плоское напряженное состояние в точке: а) площадка bc наклонена к правой грани ac под углом α > 0; б) площадка bc наклонена к правой грани ab под углом α < 0
Призма находится в равновесии. Составим уравнения равновесия (приравниваем к нулю сумму проекций всех сил на оси u и v):
∑V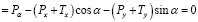 ; (14)
; (14)
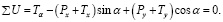 (15)
(15)
Подставим в уравнения (14) и (15) выражения сил из равенств (1):
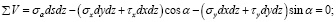
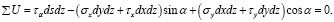
Сократив эти уравнения на dsdz, учитывая при этом, что (dy / ds) = cos α, а (dx / ds) = sin α, будем иметь
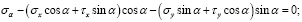
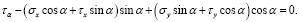
Раскрывая скобки и решая данные уравнения относительно σα и τα, получаем
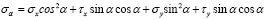 ;
;
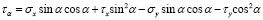 .
.
Заменяя τy на τх (они равны по модулю), окончательно будем иметь
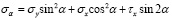 ; (16)
; (16)
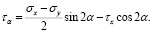 (17)
(17)
Эти формулы совпадают с формулами, выведенными в [3, с. 28], заменив τx на τхy.
Задача 4. Определение касательных и нормальных напряжений в площадках, наклоненных к правой грани элементарного параллелепипеда под углом α < 0 (рис. 2, б).
Призма находится в равновесии. Составим уравнения равновесия (приравниваем к нулю сумму проекций всех сил на оси u и v):
∑V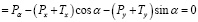 ; (18)
; (18)
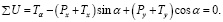 (19)
(19)
Подставим в уравнения (18) и (19) выражения сил из равенств (1):
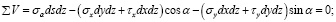
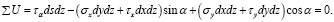
Сократив эти уравнения на dsdz, учитывая при этом, что (dy / ds) = cos α, а (dx / ds) = sin α, будем иметь:
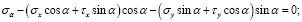
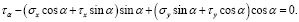
Раскрывая скобки и решая данные уравнения относительно σα и τα, получаем
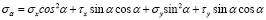 ;
;
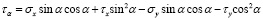 .
.
Заменяя τy на τх (они равны по модулю), окончательно будем иметь
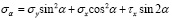 ; (20)
; (20)
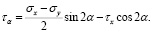 (21)
(21)
Задача 5. Определение касательных и нормальных напряжений на площадках, наклоненных к верхней горизонтальной грани элементарного параллелепипеда под углом α > 0 (рис. 3, а).
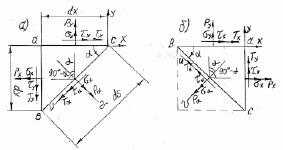
Рис. 3. Плоское напряженное состояние в точке: а) площадка bc наклонена к верхней грани ac под углом α > 0; б) площадка bc наклонена к верхней грани ab под углом α < 0
Призма находится в равновесии. Составим уравнения равновесия (приравниваем к нулю сумму проекций всех сил на оси u и v):
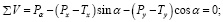 (22)
(22)
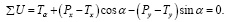 (23)
(23)
Подставим в уравнения (22) и (23) выражения сил из равенств (1):
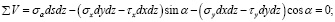
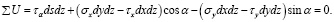
Сократив эти уравнения на dsdz, учитывая при этом, что (dy / ds) = sin α, а (dx / ds) = cos α, заменяя τy на τх и решая их относительно σα и τα будем иметь следующие уравнения:
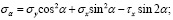 (24)
(24)
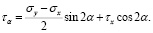 (25)
(25)
Задача 6. Определение касательных и нормальных напряжений на площадках, наклоненных к верхней горизонтальной грани элементарного параллелепипеда под углом α < 0 (рис. 3, б).
Призма находится в равновесии. Составим уравнения равновесия (приравниваем к нулю сумму проекций всех сил на оси u и v):
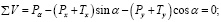 (26)
(26)
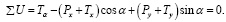 (27)
(27)
Подставим в уравнения (26) и (27) выражения сил из равенств (1):
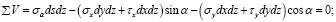
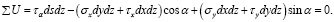
Сократив эти уравнения на dsdz, учитывая при этом, что (dy / ds) = sin α, а (dx / ds) = cos α, заменяя τy на τх и решая их относительно σα и τα будем иметь следующие уравнения:
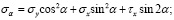 (28)
(28)
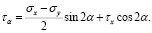 (29)
(29)
Задача 7. Определение касательных и нормальных напряжений на площадках, наклоненных к левой вертикальной грани элементарного параллелепипеда под углом α > 0 (рис. 4, а).
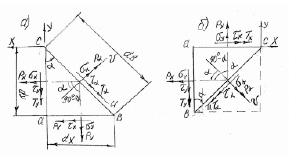
Рис. 4. Плоское напряженное состояние в точке: а) площадка bc наклонена к левой грани ac под углом α > 0; б) площадка bc наклонена к левой грани ab под углом α < 0
Призма находится в равновесии. Составим уравнения равновесия (приравниваем к нулю сумму проекций всех сил на оси u и v):
∑V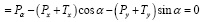 ; (30)
; (30)
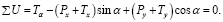 (31)
(31)
Подставим в уравнения (30) и (31) выражения сил из равенств (1):
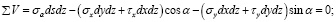
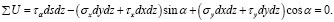
Сократив эти уравнения на dsdz, учитывая при этом, что (dy / ds) = cos α, а (dx / ds) = sin α, заменяя τy на τх и решая их относительно σα и τα будем иметь следующие уравнения:
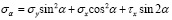 ; (32)
; (32)
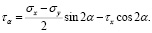 (33)
(33)
Эти формулы совпадают с формулами, выведенными в [4, с.75], заменив τх на –τ.
Задача 8. Определение касательных и нормальных напряжений на площадках, наклоненных к левой вертикальной грани элементарного параллелепипеда под углом α < 0 (рис. 4, б).
Призма находится в равновесии. Составим уравнения равновесия (приравниваем
к нулю сумму проекций всех сил на оси u и v):
∑V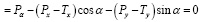 ; (34)
; (34)
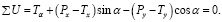 (35)
(35)
Подставим в уравнения (34) и (35) выражения сил из равенств (1):
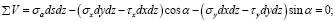
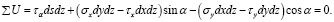
Сократив эти уравнения на dsdz, учитывая при этом, что (dy / ds) = cos α, а (dx / ds) = sin α, заменяя τy на τх и решая их относительно σα и τα будем иметь следующие уравнения:
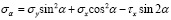 ; (36)
; (36)
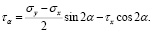 (37)
(37)
Для ускорения вычисления касательных и нормальных напряжений в площадках, наклоненных к граням элементарного параллелепипеда, при плоском напряженном состоянии составлена таблица, где в одной строке выставлены формулы и соответствующие им положения площадок относительно граней.
Пример 1. Для напряженного состояния, изображенного на рис. 5, определить напряжения σα и τα на площадке I-I, наклоненной к нижней грани под углом α = 60°, к правой грани под углом α = –30° , если σy = –500 кгс/см2 , σх = 1000 кгс/см2, τх = 250 кгс/см2.
Решение. В первой строке таблицы находим заданное положение площадки и соответствующие ему формулы для нахождения напряжений на этой площадке с наклоном 60° к нижней грани (пример 1.3 из [2. с. 114]). Подставим в эти формулы заданные напряжения σy, σх, τх и угол α в соответствии с правилом знаков
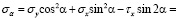
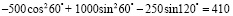 кгс/см2,
кгс/см2,
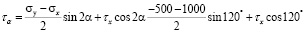 = –775 кгс/см2.
= –775 кгс/см2.
Формулы для определения напряжений в площадках, наклоненных к граням элементарного параллелепипеда, при плоском напряженном состоянии
|
№ п/п 1 |
|
|
|
2 |
|
|
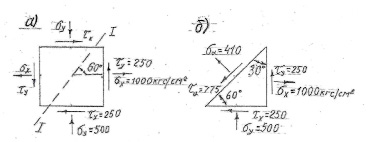
Рис. 5. Напряженное состояние в точке: а) положение площадки I-I; б) изображение напряжений на наклонной площадке
Результаты исследования и их обсуждение
При выводе формул для вычисления касательных и нормальных напряжений в площадках, наклоненных к боковым граням элементарного параллелепипеда, рассматривалось их положение под углом α > 0 и под углом α < 0. Было получено восемь пар формул. Анализ этих формул показал, что при наклоне площадки либо к нижней, либо к верхней грани формулы имеют одинаковый вид. Одинаковый вид также имеют формулы для определения напряжений на площадке, наклоненной к левой и правой вертикальной грани. Для определения напряжений в рассматриваемых площадках с использованием выведенных формул необходимо напряжения σy, σх, τх и угол α подставлять в эти формулы в соответствии с правилом знаков. Результаты исследования сведены в таблицу.
Заключение
Анализ информации из источников по сопротивлению материалов показывает, что формулы для определения напряжений в площадках, наклоненных к вертикальной левой грани и к вертикальной правой грани элементарного параллелепипеда – разные. В данной статье установлено, что формулы для определения напряжений в площадке с наклоном к левой и к правой грани одинаковы. Уменьшение формул вдвое, информация о правилах пользования формулами, представление результатов исследования в таблице для всех возможных положений наклонной площадки способствует ускорению учебных действий как одного из факторов интенсификации обучения. Результаты исследования будут полезны студентам, преподавателям, всем, кто изучает сопротивление материалов.
Библиографическая ссылка
Подобед С.А. К ОПРЕДЕЛЕНИЮ НАПРЯЖЕНИЙ В ПЛОЩАДКАХ, НАКЛОНЕННЫХ К БОКОВЫМ ГРАНЯМ ЭЛЕМЕНТАРНОГО ПАРАЛЛЕЛЕПИПЕДА, ПРИ ПЛОСКОМ НАПРЯЖЕННОМ СОСТОЯНИИ // Современные наукоемкие технологии. 2022. № 12-2. С. 363-371;URL: https://top-technologies.ru/ru/article/view?id=39486 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.39486