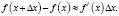На современном этапе в связи с модернизацией образования появляются новые подходы к развитию всей системы обучения. Взаимосвязанными звеньями в этом процессе выступают общее образование и высшее педагогическое образование. В среднем математическом образовании сегодня одним из приоритетных направлений является подготовка обучающихся к использованию математики в решении проблем, возникающих в реальной действительности вне рамок образовательного процесса [1, с. 5], то есть формирование у них прикладных умений, в частности умений решать практико-ориентированные задачи и использовать математический подход в разных ситуациях: в рассуждении, обосновании, аргументации, планировании, оценках и т.д.
«Сегодня нужны функционально грамотные выпускники, способные вступать в отношения с внешней средой, быстро адаптироваться и функционировать в ней» [2, с. 2].
Это обусловлено возрастанием в последние десятилетия роли математики в общей системе знаний. Математические методы используются сегодня в разных сферах деятельности. Математика составляет основу современных информационных технологий [1].
В ФГОС среднего общего образования специально выделено требование к предметным результатам освоения курса математики: «сформированность умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат» [3]. Отсюда следует, что формирование умений строить математические модели простейших реальных явлений, исследовать явления по готовым моделям, применять эти умения на практике является основной целью обучения математике в современной школе. Для достижения этой цели учителю математики необходимо познакомить школьников с главным методом математики – математическим моделированием. При этом он сам должен хорошо владеть данным методом, использовать его при решении практико-ориентированных задач.
Цель исследования – разработать модель эффективного формирования у студентов педагогического направления приемов математического моделирования средствами математического анализа в процессе решения практико-ориентированных задач.
Материал и методы исследования
Использовались материалы ФГОС среднего общего образования и ФГОС ВО по направлению Педагогическое образование. Проводился анализ содержания математических дисциплин и выявлялись их возможности для формирования у студентов приемов математического моделирования: наличие практико-ориентированных задач; приемы овладения действиями, необходимыми для математического моделирования, и т.д. Для получения результатов, кроме теоретических методов, применялись экспериментальные методы: наблюдение за процессом решения математических задач студентами; беседы с учителями школ, анкетирование учащихся, анализ и обобщение собственного опыта преподавания математических и методических дисциплин в педвузе.
Результаты исследования и их обсуждение
В научной литературе есть разные трактовки понятий «математическая модель», «математическое моделирование», хотя сущность их одна и та же. В «Математической энциклопедии» (т. 3) дано такое определение:
«Математическая модель – это приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики» [4, с. 574].
Существуют разные виды моделей: модель-заместитель, модель-представление, модель-интерпретация, исследовательская модель. Деятельность по построению (или выбору) одной из указанных моделей называется моделированием. Математическое моделирование применяется для познания внешнего мира, оно позволяет проникнуть в сущность изучаемых явлений и процессов, прогнозировать многие явления, управлять ими.
Общий подход к построению математической модели изучаемого объекта описал в своей работе А.Д. Мышкис [5]. Рассматривая применение метода математического моделирования, он выделяет три этапа [5, с. 9]. Первый этап посвящен уточнению проблемы и построению содержательной модели объекта, переводу ее на формальный математический язык. На втором этапе происходит изучение построенной математической модели путем решения полученной математической задачи. Третий этап посвящен переводу результата решения задачи на язык той науки, на котором была сформулирована исходная проблема.
Некоторые ученые разделяют процесс математического моделирования на четыре основных этапа. Так, А.Н. Тихонов выделяет следующие этапы: «первый – установление законов, связывающих объекты модели; второй – решение математических задач внутри построенной модели; третий – согласование результатов наблюдений или измерений параметров реальных объектов с теоретическим исследованием построенной модели; четвертый – уточнение и модернизация модели на основании результатов, полученных на третьем этапе» [1, с. 222]. Оба подхода не противоречат друг другу.
В методической литературе по методике обучения математике выделяют обычно три этапа математического моделирования текстовых (сюжетных) задач: 1) формализация (построение математической модели задачи); 2) решение задачи внутри модели, то есть математическими средствами; 3) интерпретация полученного математического решения. Указанные этапы проиллюстрированы нами в работе [6] при построении геометрических моделей и применении геометрического метода в решении алгебраических задач школьного курса математики.
Учитывая значимость умений математического моделирования для современного образованного человека, в научно-методической литературе широко обсуждаются вопросы формирования компетенции математического моделирования у учащихся средней школы и студентов вузов (О.С. Бабанская, М.В. Егупова, Ю.Б. Мельников, А.Д. Нахман, А.Г. Мордкович, М.А. Осинцева, Н.И. Светлова, Е.И. Скафа и др.).
Выделяют следующие компоненты компетенции математического моделирования: 1) мотивационно-ценностный компонент, предполагающий понимание универсальности математического языка, необходимости формализации законов физики, химии, биологии, экономики; 2) кругозор и постоянное его расширение, которое обязательно сопровождается такими формами мыслительной деятельности, которые необходимы в процессе математического моделирования (анализ явлений и процессов, сравнительные характеристики, логические умозаключения и т. п.); 3) знания и умения: этот компонент направлен на актуализацию предметных знаний и умений применительно к выбранной модели, а также коммуникативных умений и умений применять в процессе моделирования современные информационные технологии; 4) опыт деятельности в области моделирования, который способствует переносу математических знаний и умений на незнакомые ситуации, в том числе возникающие в практической деятельности; 5) рефлексия – важнейший компонент компетенции математического моделирования, способствующий развитию таких качеств личности, как самоконтроль, ответственность, рациональность, самостоятельность [7].
В обучении математике метод математического моделирования целесообразно формировать у учащихся в процессе решения практико-ориентированных задач. Практико-ориентированная задача – это вид текстовых задач, для решения которых необходима реализация всех этапов математического моделирования. Это задачи из окружающей действительности, которые тесно связаны с формированием практических навыков, необходимых в том или ином виде профессиональной деятельности и в повседневной жизни.
В школьном курсе математики и в вузовских математических курсах представлены в основном уже готовые математические задачи, в решении которых отсутствует первый этап математического моделирования, поэтому обучающиеся часто испытывают значительные трудности при решении практико-ориентированных задач, особенно на этапе формализации. Об этом свидетельствуют и ежегодные результаты ЕГЭ по математике профильного уровня.
В ликвидации имеющихся пробелов в обучении математическому моделированию школьников большая роль принадлежит учителю: необходимо, чтобы он сам владел приемами математического моделирования, в том числе при решении практико-ориентированных задач. В научно-методической литературе последних лет много внимания уделяется обучению математическому моделированию студентов инженерно-технических и экономических профилей [8, 9, 10]. Проблема формирования умений математического моделирования у будущих педагогов исследована, на наш взгляд, недостаточно. В частности, не выделены приемы математического моделирования, которые используются в процессе решения практико-ориентированных задач, и составляющие их действия. Не определены типы задач, которые необходимо решать для формирования выделенных действий, и т. д.
Как показывает практика, студенты с интересом решают и воспринимают практико-ориентированные задачи, особенно те, содержание которых раскрывает приложения математики в окружающей нас действительности, в смежных дисциплинах, знакомит с использованием ее в разных сферах современного производства. Например, в процессе изучения математического анализа в педвузе можно использовать разные типы практико-ориентированных задач, направленных на формирование приемов математического моделирования. Наиболее часто встречаются текстовые задачи производственного характера из области: а) сельского хозяйства; б) деревообработки; в) строительства; г) мелиорации; д) транспорта; е) гидротехники и др.
В ходе исследования нами были выделены приемы математического моделирования средствами математического анализа, которые возможно формировать у студентов при решении указанных типов практико-ориентированных задач. К ним относятся приемы:
– составление функции и исследование ее элементарными средствами;
– составление числовой последовательности и нахождение ее предела;
– составление функции и использование формулы Лагранжа;
– составление функции и исследование ее с помощью производной;
– составление функции и нахождение ее наибольшего или наименьшего значения;
– использование определенного интеграла;
– использование формулы и ряда Тейлора;
– использование двойного интеграла и др.
Приемы математического моделирования в процессе решения практико-ориентированных задач и составляющие их действия
|
№ п/п |
Название приема |
Действия, составляющие прием |
|
1. |
Составление функции и исследование ее элементарными средствами |
1. Определение функциональной зависимости величин по условию задачи. 2. Составление функции, выражающей зависимость между величинами. 3. Исследование функции и построение ее графика (если это необходимо) |
|
2. |
Составление числовой последовательности и нахождение ее предела |
1. Определение формы заданного объекта (если это необходимо). 2. Определение функциональной зависимости величин и составление последовательности (функции). 3. Исследование последовательности (на возрастание или убывание, ограниченность и т.д.). 4. Нахождение предела последовательности (если это необходимо) |
|
3. |
Составление функции и использование формулы Лагранжа |
1. Определение зависимости и составление функции по условию задачи. 2. Нахождение приращения функции Δf(x) при условии приращения аргумента x на Δx. 3. Использование формулы конечных приращений Лагранжа:
4. Выполнение необходимых преобразований и вычислений |
|
4. |
Составление функции и исследования ее с помощью производной |
1. Определение зависимости и составление функции по условию задачи. 2. Нахождение производной полученной функции. 3. Исследование функции с помощью производной |
|
5. |
Составление функции и нахождение ее наибольшего или наименьшего значения |
1. Выявление величины, о наибольшем или наименьшем значении которой говорится в задаче. 2. Выбор аргумента, т.е. независимой переменной, и указание промежутка его допустимых значений. 3. Выражение искомой величины как функции введенного аргумента. 4. Нахождение наибольшего или наименьшего значения функции на заданном промежутке; если промежутком является интервал, то следует исследовать функцию на экстремум: в точке максимума функция принимает наибольшее значение, а в точке минимума – наименьшее. 5. Интерпретация полученного результата и ответ на вопрос задачи |
|
6. |
Использование определенного интеграла |
1. Выявление искомой величины. 2. Определение формулы для нахождения этой величины с помощью интеграла. 3. Выполнение необходимых преобразований и вычислений |
|
7. |
Использование формулы и ряда Тейлора |
1. Определение функции по условию задачи. 2. Составление формулы Тейлора с остаточным членом в форме Лагранжа. 3. Оценивание допускаемой погрешности вычислений |
|
8. |
Использование двойного интеграла |
1. Оптимальный выбор прямоугольной системы координат. 2. Определение формулы для вычисления искомой величины с помощью двойного интеграла. 3. Выполнение необходимых преобразований и вычислений |
Действия, входящие в состав каждого приема, приведены в таблице.
В таблице приведены лишь приемы математического моделирования практико-ориентированных задач средствами математического анализа, аналогично можно выделить приемы и составляющие их действия в процессе изучения других дисциплин.
При формировании приемов математического моделирования в процессе решения практико-ориентированных задач необходимо соблюдать следующие этапы: подготовительный, мотивационный, ориентировочный, этап формирования отдельных действий, составляющих прием, формирование приема в целом.
Раскроем содержание названных этапов.
1. Подготовительный этап. На этом этапе происходит предварительное усвоение определенных знаний и умений, составляющих теоретический базис приема. Подготовительный этап в процессе обучения явно не выделяется, так как здесь происходит усвоение знаний и умений, предусмотренных программой по дисциплине.
2. Мотивационный этап. На этом этапе следует убедить студентов – будущих педагогов в необходимости овладения данным приемом.
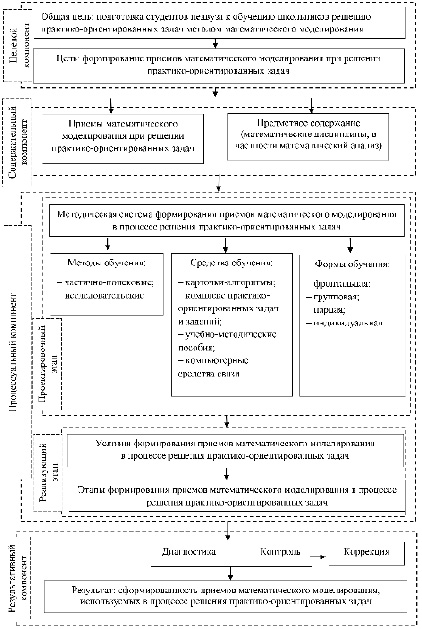
Рис. 1. Модель формирования приемов математического моделирования у студентов в процессе решения практико-ориентированных задач
Для этого можно использовать как задачи из школьного курса математики или материалов ОГЭ и ЕГЭ, так и задачи из других научных областей, из практики (разных отраслей производства), которые убеждают в необходимости овладения действиями, составляющими данный прием.
3. Ориентировочный этап. На этом этапе студенты должны выделить действия, составляющие прием математического моделирования. Это можно сделать путем ретроспективного анализа решения практико-ориентированных задач данного типа.
4. Этап формирования отдельных действий, составляющих прием. На данном этапе, используя несложные текстовые задачи в одно, два действия, следует организовать формирование отдельных действий изучаемого приема.
5. Этап формирования приема в целом. Целью этого этапа является синтезирование отдельных действий (умений) в целостный прием. Здесь следует использовать практико-ориентированные задачи из разных областей, решение которых требует применения значительного количества действий, составляющих прием.
Будущие педагоги должны усвоить схему поэтапного формирования приемов математического моделирования, которую они смогут применять в обучении школьников данному виду деятельности. В частности, они должны понимать, что этапы формирования приемов в обучении не следует резко отделять друг от друга, так как они тесно связаны между собой. Не стоит также строго разделять задачи, используемые на каждом из этих этапов, главное – понимать ведущую цель каждого этапа и способы ее достижения.
В целом, формирование приемов математического моделирования в процессе решения практико-ориентированных задач можно представить в виде модели (рис. 1).
Приведем примеры, иллюстрирующие приемы математического моделирования, которые можно использовать в процессе изучения математического анализа в педвузе. Например, при изучении последовательности и ее предела можно предложить студентам решить следующую текстовую задачу.
Задача 1 (из области лесозаготовок). Бревна и дрова на складах лесоматериалов укладывают в штабеля (поленницы) различной формы. Докажите, что значения коэффициента полнодревесности поленницы треугольного профиля, составленной из одинаковых цилиндрических чурок (рис. 2), не выходят из интервала (0,60; 0,91) [11].
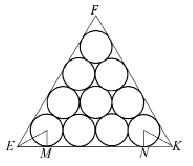
Рис. 2. Штабель с дровами
У к а з а н и е. Учет уложенных в штабеля лесоматериалов ведется с помощью коэффициента полнодревесности штабеля, под которым понимается отношение объема древесины в штабеле к геометрическому объему штабеля.
Доказательство
Для решения задачи необходимо выполнить действия:
1) Определить форму заданного объекта. Данная поленница представляет собой «лежащую на боку» правильную треугольную призму.
2) Определить зависимость величин и составить функцию. Если в первом ряду поленницы уложено k чурок, то во втором ряду их k – 1 , в третьем k – 2, в последнем 1. Общее количество чурок в поленнице:
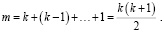
Тогда коэффициент полнодревесности поленницы будет равен:
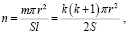
где l – длина поленницы, r – радиус чурки, S – площадь поперечного сечения поленницы, т.е. площадь треугольника EFK.
Так как:
= 
,
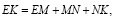
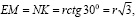
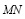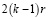то
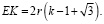
Cледовательно:
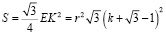
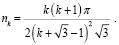
Получили последовательность nk. Из формулы ясно, что коэффициент полнодревесности поленницы зависит только от количества k чурок в первом ряду и не зависит от их радиуса.
2) Исследовать последовательность на монотонность: исследуем последовательность nk на возрастание путем определения знака разности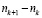 
и нахождения ее нижней грани. Она равна 0,60.
Чтобы получить оценку сверху, найдем предел последовательности nk.
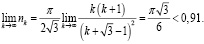
В данном случае при решении задачи использовался прием математического моделирования – составление числовой последовательности и нахождение ее предела. Кроме того, студенты расширили свои познания в профессиональной области лесозаготовок.
Большие возможности для формирования приемов математического моделирования предоставляют практико-ориентированные задачи на оптимизацию. В школьном курсе математики это текстовые задачи на нахождение наибольшего или наименьшего значения. Большинство из них решаются с помощью производной по приведенному алгоритму (см. п. 5 таблицы 1). Приведем примеры.
Задача 2 (из области сельского хозяйства). Из трех досок одинаковой ширины сколачивается водопойный желоб для коров. При каком угле α наклона боковых стенок к основанию водопойный желоб будет иметь наибольшую вместимость?
Решение. Данная задача на нахождение наибольшего значения. Для построения ее математической модели необходимо выполнить действия.
1) Выявить величину, о наибольшем значении которой говорится в задаче. В задаче говорится о наибольшей вместимости желоба, который в сечении имеет форму равнобедренной трапеции, причем одно основание желоба равно боковой стороне (рис. 3).
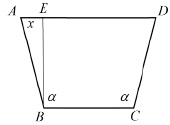
Рис. 3. Модель желоба
2) Выбрать независимую переменную (аргумент) и указать интервал ее изменения. Обозначим острый угол трапеции через x, где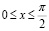 
.
3) Выразить величину, о наибольшем значении которой говорится в задаче, как функцию введенного аргумента. Если ширина досок, из которых сколачивается желоб, равна a (AB = BC = CD = a), а острый угол трапеции равен x, то площадь трапеции равна:
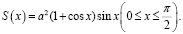
Таким образом, функция по условию задачи составлена, найдем наибольшее значение этой функции на указанном промежутке.
4) Найти наибольшее значение функции на заданном промежутке. Исследуем функцию на экстремум с помощью производной:
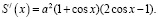
Так как на отрезке [0; π / 2 ] одна стационарная точка x = π / 3, a S(0) = 0 ,
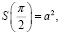
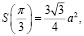
то наибольшее значение S принимает при x = π / 3 или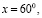 
тогда 
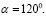
Аналогично по такому же алгоритму решается следующая задача.
Задача 3 (из области деревообработки). На лесопильных рамах, которые предназначены для продольного пиления, бревна часто распиливают на квадратный брус и четыре доски (рис. 4) с максимально возможной площадью поперечного сечения. Какой толщины получатся доски при такой распиловке из бревна диаметром d [11]?
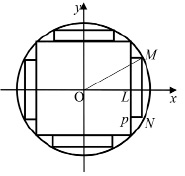
Рис. 4. Модель бруса и досок
«Результат, полученный в ходе решения этой задачи, имеет большое значение для практики. Он позволяет до распиловки бревна определить, будут ли полученные доски отвечать установленным стандартам, т.е. приемлем ли для данного бревна такой раскрой. Знание толщины досок необходимо еще и для правильной установки пил» [11, с. 22].
Задачи на оптимизацию часто возникают в области транспорта. Например, «при проектировании дорог появляется необходимость соединить подъездным путем тот или иной объект с автомагистралью. Различные экономические расчеты в таких случаях показывают, что подъездной путь должен пойти не перпендикулярно к магистрали, а под некоторым острым углом, который называется углом примыкания подъездного пути к магистрали» [11, с. 27].
Задача 4 (из области транспорта).
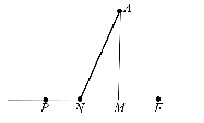
Рис. 5. Геометрическая модель к задаче 4
Центральная усадьба агрокомплекса A (рис. 5) расположена в 50 км от райцентра P и в 30 км от магистрали, проходящей через райцентр. Под каким углом к магистрали следует провести подъездной путь из A, чтобы стоимость перевозок груза из A в P и из P в A была наименьшей, если известно, что перевозка по магистрали будет обходиться агрокомплексу в 2 раза дешевле, чем по подъездному пути?
Решение. Данная задача на нахождение наименьшего значения величины. Для построения ее математической модели необходимо выполнить следующие действия.
1) Выявить величину, о наименьшем значении которой говорится в задаче. В задаче говорится о наименьшей стоимости перевозок груза.
2) Выбрать независимую переменную и указать интервал ее изменения. Пусть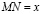 
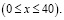
3) Выразить величину, о наименьшем значении которой говорится в задаче, как функцию введенного аргумента.
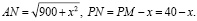
Если обозначить стоимость перевозки 1 т груза на 1 км по магистрали q, тогда стоимость перевозки 1 т груза от P до A (или в обратном направлении) будет равна:
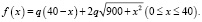
Итак, функция составлена, надо найти ее наименьшее значение на отрезке [0; 40].
4) Найти наименьшее значение функции на заданном промежутке. Исследуем составленную функцию с помощью производной:
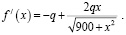
На данном промежутке у функции f(x) одна стационарная точка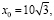 
причем
,
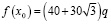а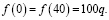 
Поэтому в точке x0 функция принимает наименьшее значение. Тогда угол примыкания:
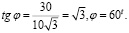
Практико-ориентированные задачи из области мелиорации, гидротехники также могут быть использованы для формирования приемов математического моделирования. В качестве математической модели здесь выступает интеграл от составленной функции. Приведем пример задачи, в которой используется определенный интеграл.
Задача 5 (из области мелиорации). Найдите площадь сечения канала параболического профиля, наибольшая глубина которого h, а ширина b.
Иногда для решения практико-ориентированной задачи используется математическая модель в виде двойного интеграла. Приведем пример.
Задача 6 (из области грузового транспорта). Найдите среднюю дальность ездки при транспортировке зерна (от комбайна) с квадратного поля (сторона квадрата a) к дороге, совпадающей с одной из сторон квадрата.
Решение. Пусть оси координат – стороны квадрата, а дорога совпадает с осью абсцисс. Тогда из точки M(x;y) поля зерно перевозится на расстояние y. Поэтому совершаемая при этом работа равна:
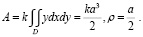
Мы привели примеры формирования у будущих педагогов приемов математического моделирования текстовых задач лишь средствами математического анализа. Перечень таких задач можно было бы продолжить, если включить в него сюжетные задачи из школьного курса математики или других математических дисциплин.
Заключение
В условиях педагогического образования на современном этапе метод математического моделирования выступает как фактор преемственности обучения математике не только между средней школой и вузом, но он имеет и обратное направление, реализующее преемственность между вузом и школой. Актуальность формирования данного метода у будущих педагогов значительно возросла в связи с широким применением практико-ориентированного обучения математике в школе. Как показало наше исследование, формирование приемов математического моделирования необходимо осуществлять по действиям, составляющим каждый прием, в соответствии с выделенными этапами. В качестве средств следует использовать практико-ориентированные задачи из разных профессиональных областей, что будет способствовать не только закреплению и углублению теоретических знаний студентов педвуза, овладению математическими умениями и навыками, но и знакомству их с особенностями будущих профессий школьников. Кроме этого, в процессе решения практико-ориентированных задач у них формируются некоторые методические умения и навыки (например, они запоминают этапы решения задачи, общую схему формирования приемов математического моделирования). Учебный процесс в таком случае приближается к реальным жизненным условиям, что способствует овладению студентами общеучебными умениями и навыками, развитию их инициативы и самостоятельности.
Исследование выполнено в рамках гранта на проведение научно-исследовательских работ по приоритетным направлениям научной деятельности вузов-партнеров по сетевому взаимодействию (Чувашский государственный педагогический университет им. И.Я. Яковлева и Мордовский государственный педагогический университет имени М.Е. Евсевьева) по теме «Формирование приемов математического моделирования у студентов педагогического направления в процессе решения практико-ориентированных задач».
Библиографическая ссылка
Капкаева Л.С. ФОРМИРОВАНИЕ ПРИЕМОВ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ У СТУДЕНТОВ ПЕДАГОГИЧЕСКОГО НАПРАВЛЕНИЯ В ПРОЦЕССЕ РЕШЕНИЯ ПРАКТИКО-ОРИЕНТИРОВАННЫХ ЗАДАЧ // Современные наукоемкие технологии. – 2022. – № 12-2. – С. 323-331;URL: https://top-technologies.ru/ru/article/view?id=39480 (дата обращения: 21.11.2024).