Современное образовательное пространство формируется педагогами, обучающимися, содержанием научных дисциплин и способами их взаимодействия. Математическое образование, являющееся необходимым условием технологического прогресса, требует особого внимания. Поэтому в обучении математике как школьников, так и студентов важно большое внимание уделять развитию у них логического, эвристического, алгоритмического и других видов мышления. Огромные надежды в достижении этих целей возлагаются на педагогов. Поэтому методическая подготовка будущих учителей математики – это одна из важнейших задач, стоящих перед преподавателями вузов [1].
Методическая подготовка студентов предполагает, прежде всего, формирование у них методических компетенций в области использования и разработки упражнений, различных приемов и в целом технологий обучения [2]. Поэтому проблема поиска методических приемов и средств формирования методических компетенций студентов является актуальной.
Обращаясь к понятию «методическая компетенция», отметим, что это не что иное, как «совокупность методологических, предметных, методических и технологических знаний, определенных умений, ценностных отношений, опыта творчества, а также набор профессионально значимых качеств личности» [3].
Обучение студентов должно строиться на деятельностной основе, предполагающей не только воспроизведение изученных подходов, концепций, но и формирование методических способов действий, адекватных изучаемому содержанию. Такая образовательная траектория предполагает обучение студентов методическим приемам по проектированию обучающих средств.
Несомненно, формирование методических компетенций будущих педагогов, учителей математики, возлагается, прежде всего, на преподавателей математических и методических дисциплин. Значительная роль среди прочих методических курсов отведена методике обучения математике. Содержание курса достаточно объемно. В данной статье мы остановимся на таком его разделе, как «Методика обучения учащихся действиям над числами». Центральным здесь является обучение учащихся открытию, усвоению и применению изучаемых математических правил (алгоритмов). Некоторые рекомендации, способы конструирования обучающих средств, системы заданий для обучения учащихся действиям над числами приведены в работах [4–6]. Опираясь на проведенные в этой области исследования, мы постараемся поэтапно описать процесс конструирования заданий для обучающихся как основы построения технологий обучения математическим алгоритмам (правилам).
Цель исследования – выявить методические приемы конструирования заданий для обучения учащихся математическим алгоритмам.
Материалы и методы исследования
В статье использованы материалы, полученные в ходе исследования, проведенного со студентами и преподавателями физико-математического факультета ФГБОУ ВО «Мордовский государственный педагогический университет имени М.Е. Евсевьева». Приемы анализа методической, научной литературы, наблюдение и многолетний опыт ведения математических и методических дисциплин послужили основой описываемого в статье исследования.
Материалы статьи обладают методической значимостью для педагогов высшей школы. Разработанные приемы предназначены не только для будущих учителей математики, но и для действующих.
Результаты исследования и их обсуждение
В данной статье мы подробно охарактеризуем методические приемы конструирования заданий для обучения учащихся 5–6 классов математическим правилам или алгоритмам действий над числами. Приведем методические рекомендации по обучению студентов данным приемам. Также отметим, что на занятиях со студентами эффективно использование таких образовательных технологий, которые нами охарактеризованы в статьях [7, 8].
Начнем с того, что формирование методических компетенций должно опираться на определенную теоретическую базу. Так, к опорным математическим знаниям и умениям студентов мы отнесем: знания о понятии алгоритма, его свойствах; знания о замкнутости алгебраических операций над числами; умение отличать правила от алгоритмов; умение выполнять классификации чисел по различным основаниям.
Формирование названных понятий и способов действий на более высоком уровне происходит при изучении курса «Алгебра и теория чисел». Так, при изучении темы «Основные алгебраические структуры» у студентов формируются понятия групп и полей, происходит первое полноценное знакомство с понятием математического алгоритма, с его шагами, обоснованием и построением. Так, алгоритм действий над целыми числами строится в ходе построения кольца целых чисел методом пар (симметризации абелева моноида). Здесь же вводятся новые кольцевые операции над парами целых чисел. Система предлагаемых практических задач на занятиях курса алгебры и теории чисел на действия с целыми числами в расширенном кольце ℕ×ℕ должна совпадать по структуре со школьными задачами по данной теме. Этим обеспечивается преемственность в обучении на уровне школа – вуз, а в случае педагогического вуза – и обратная связь школа – вуз – школа.
При изучении рациональных чисел прием метода пар используется уже для кольца целых чисел, на основе которого симметризацией относительно умножения строится поле рациональных чисел, являющееся основным математическим объектом в школе до 8 класса. Основным этапом методико-математической пропедевтики на данном этапе является задание для студентов на формулирование алгоритма действий над целыми (рациональными) числами, универсального для школьного и вузовского случая (с заменой понятий и обозначений) и проведения сравнительного анализа.
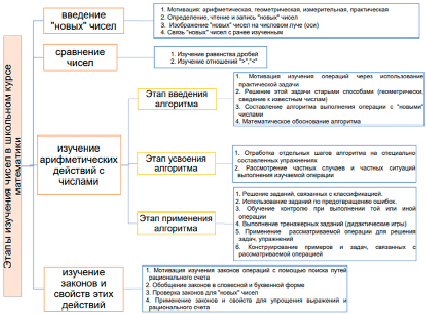
Рис. 1. Этапы изучения чисел
Опорными методическими знаниями и умениями студентов к моменту построения методики обучения учащихся правилам действий над числами являются: знания о структуре, особенностях построения современного урока математики; умения осуществлять логико-дидактический анализ школьного учебника математики; этапы решения математических задач; умения подбирать задания для изучения той или иной дидактической единицы.
Основное изучаемое содержание, необходимое для формирования указанных методических компетенций, это знание схемы изучения чисел (рис. 1), содержания этапов изучения алгоритмов, знания методических особенностей их реализации.
На первом этапе формирования названных методических компетенций необходимо сформировать умения анализировать учебное содержание школьных учебников математики, определять подходы, реализованные в них. На втором этапе необходимо обучить студентов конструированию заданий, опираясь на перечень выделенных методических действий. В дальнейшем нужно перейти к проектированию уроков математики.
Начнем с описания общего приема конструирования заданий для обучения алгоритмам действий над числами:
1. Выясните, как реализованы шаги по введению, усвоению и применению алгоритма в школьном учебнике математике.
2. Разработайте задания для введения алгоритма.
3. Разработайте задания для усвоения алгоритма.
4. Разработайте задания для применения алгоритма.
Далее приведем реализацию наиболее важных и сложных в реализации шагов обозначенного нами приема. Каждый из названных шагов можно описать в виде действий, составляющих частные приемы разработки заданий для обучения школьников алгоритмам.
Прием анализа школьного учебника математики по введению алгоритма
1. Выясняем, подчеркивается ли значимость изучения «новой» операции над числами, создается ли проблемная ситуация, связанная со сложностью выполнения определенных действий с числами.
2. Выясняем, приводится ли задача практического, геометрического или прочего содержания. Если же задача не сформулирована, то отмечаем, можно ли ее выделить из описываемой в учебнике практической (геометрической) ситуации.
3. Выясняем способ решения предложенной задачи (без знания шагов изучаемого алгоритма).
4. Выясняем, указаны ли шаги изучаемого алгоритма (либо отмечаем, что приведено правило или же алгоритмическое предписание).
5. Определяем, что является математическим обоснованием алгоритма (приведено ли оно в учебнике).
Приведем пример анализа школьного учебника математики на рис. 2. Подчеркнем, что анализ учебника в плане усвоения алгоритма предполагает выделение упражнений для усвоения каждого из его шагов (если они сложны) и в целом выполнение этих и только этих действий с различными числами.
Напомним, что анализ учебника – отправная точка в конструировании не только заданий, но и уроков. Так, результатом использования указанного приема будет выделение опорных знаний и умений школьников согласно подходу, отраженному в учебнике. Они уже определены ранее известным способом решения задачи, а также действиями, описанными в шагах алгоритма, в его математическом обосновании. Как правило, студенты затрудняются выстроить систему заданий так, чтобы актуализировать у учащихся необходимые знания и умения, применить их для решения некоторой задачи, вызвать затруднение в пробном учебном действии и преодолеть его, введя шаги алгоритма или сформулировав правило. Предложенный далее прием помогает студентам справиться с названными затруднениями.


Рис. 2. Описание реализации этапов введения и усвоения алгоритма
Прием конструирования заданий для «открытия» шагов алгоритма
1. Подберите (сконструируйте) задания для актуализации опорных знаний и умений при изучении алгоритма.
2. Подберите (составьте) задачу, в которой три и более случая на выполнение изучаемой операции. В формулировке задачи можете указать способ ее решения (ранее известный школьникам). Предусмотрите включение в систему заданий ситуации, которую сложно разрешить ранее известным способом (или обосновать справедливость его применения).
3. Сформулируйте задание, в котором учащиеся выполнят анализ полученных решений (записей). Одним из требований такого задания должно быть: «Сформулируйте правило» («Сформулируйте шаги алгоритма»).
Например, для открытия правила умножения дроби на число можно предложить задание, аналогичное тому, которое приведено в учебнике: «Найдите периметр квадрата со стороной, равной: а) 25 см; б) 3/7 см; в) 5/16 см; г) 225/9999 см». Актуализация определения произведения натуральных чисел, знание формул нахождения периметра квадрата помогает ученикам выдвинуть предположение о том, что сумму четырех одинаковых чисел можно заменить произведением этого числа и числа четыре. Затем, проведя анализ полученных записей, ученики легко формулируют правило умножения дроби на число.
Приведем также некоторые рекомендации по конструированию заданий для усвоения алгоритма и для его применения:
− предложите различные ситуации для усвоения шагов алгоритма (предписания);
− подберите или составьте задания для самостоятельной работы, домашней работы и этапа актуализации для следующего урока;
− подберите или разработайте задания на применение алгоритма в простейших ситуациях: текстовые задачи, уравнения (неравенства), задания, содержащие буквы, задания вида «найди и исправь ошибки»;
− подберите или разработайте задания на применение алгоритма в более сложных ситуациях: на поиск закономерностей, на выявление новых свойств изучаемых объектов, способов действий с числами.
Отметим, что большинство заданий есть в школьных учебниках, их только нужно распределить по выполняемым им функциям.
Охарактеризованная нами деятельность предваряет конструирование уроков по изучению математических алгоритмов. Приведенные приемы являются основой для разработки содержания этапов уроков по изучению правил действий над числами. Также описанные приемы позволяют легко спроектировать самостоятельную деятельность учащихся с использованием различных средств. Подтверждение сказанному приведено в таблице. В ней отражена согласованность этапов урока и начальных этапов изучения алгоритма. На последующих уроках происходит применение алгоритма в более сложных ситуациях.
Соотнесение этапов урока с этапами изучения алгоритма
|
Этапы урока |
Этапы изучения алгоритма |
|
Актуализация опорных знаний, способов действий |
Решение задачи с опорой на ранее изученные знания и способы действий |
|
Постановка учебных задач |
Мотивация введения алгоритма |
|
Решение учебных задач |
Выделение шагов алгоритма Усвоение алгоритма Применение алгоритма в стандартных ситуациях |
|
Рефлексия |
Оценивание своей деятельности по решению учебных задач |
Заключение
Формирование методических компетенций в курсе методики обучения математике базируется на теоретических знаниях курса, а также обусловлено овладением специальных методических действий по его применению на практике. Большую практическую значимость, как показывает опыт работы, показали описанные в статье методические приемы конструирования заданий для обучения математике учащихся 5–6 классов.
Выделенные приемы и приведенные рекомендации способствуют формированию у студентов умений анализировать учебную литературу, отбирать математическое содержание для достижения целей урока, строить активную познавательную деятельность учащихся при изучении математических правил (алгоритмов). Действия, описанные в данных приемах, созвучны с действиями, реализующими определенные этапы уроков, в частности уроков открытия нового знания. Сказанное подтверждает, что они являются основой построения технологий обучения математике учащихся 5–6 классов.
Исследование проведено в рамках гранта на проведение научно-исследовательских работ по приоритетным направлениям научной деятельности вузов – партнеров по сетевому взаимодействию (Чувашский государственный педагогический университет имени И.Я. Яковлева и Мордовский государственный педагогический университет имени М.Е. Евсевьева) по теме «Теория и технология формирования методических компетенций студентов-математиков педвуза».
Библиографическая ссылка
Сарванова Ж.А., Ладошкин М.В., Храмова Н.А. МЕТОДИЧЕСКИЕ ПРИЕМЫ КОНСТРУИРОВАНИЯ ЗАДАНИЙ ДЛЯ ОБУЧЕНИЯ УЧАЩИХСЯ МАТЕМАТИЧЕСКИМ АЛГОРИТМАМ // Современные наукоемкие технологии. 2022. № 12-1. С. 148-153;URL: https://top-technologies.ru/ru/article/view?id=39452 (дата обращения: 01.02.2026).
DOI: https://doi.org/10.17513/snt.39452



