В связи с развитием STEM-образования получила развитие концепция персонализации инженерной подготовки, которую невозможно осуществить без дифференциации подготовки студентов технических вузов по математическим дисциплинам. Основой этой дифференциации должно стать представление преподавателей об уровне математической культуры студентов. В силу ряда причин невозможно получить достоверную оценку уровня математической культуры, основываясь только на результатах ЕГЭ по математике. Также невозможно достоверно оценить уровень математической культуры по ответам на входные тесты по математике, которые преподаватели вуза предлагают студентам, проводя «аудит» баллов ЕГЭ. Авторы дают примеры достаточно простых математических заданий, анализируя решение которых преподаватели могут оценить уровень математической культуры студентов, приступивших к освоению математических дисциплин. Также преподаватели имеют возможность контролировать процесс дальнейшего формирования математической культуры студентов в ходе освоения ими математического анализа, линейной алгебры и теории вероятностей. Авторы показывают в статье, что студенты с высоким уровнем математической культуры демонстрируют не только правильное решение заданий, но и рациональные способы этого решения. Признаком высокого уровня математической культуры является умение сопоставлять теоретические положения с практикой решения, а также записывать ответы в лаконичной форме, которая не допускает дальнейших упрощений. Студенты, использующие творческий подход, обладают, с точки зрения авторов, наивысшим уровнем математической культуры. Множество авторов, как в России [1], так и за рубежом [2], исследовали формирование математической культуры школьников, студентов и выпускников университетов. Прежде всего, исследователи задаются вопросом: что такое математическая культура? По мнению современных исследователей, это целостное образование в структуре личности, являющееся частью общей культуры, охватывающей математические понятия и компетенции. Ю.К. Чернова и С.А. Крылова расширяют понятие математической культуры, подчеркивая необходимость обладания математическим мышлением и готовностью к саморазвитию [3]. Современные исследователи выявили еще два аспекта математической культуры. Прежде всего, речь идет о математической этике [4]. Без математиков было бы невозможно построение финансовых пирамид, которые выгодны для их создателей, но разоряют доверчивых вкладчиков. Именно с помощью математиков разрабатывается таргетированная реклама, в том числе и политическая, которая помогает заказчикам манипулировать сознанием клиентов [5]. Второй аспект является позитивным. Он обобщает идею саморазвития, приписывая носителям математической культуры стремление к творчеству [6].
Дискуссии по вопросу о содержании математической культуры были актуальны в начале XX в. в связи с повышением роли прикладной математики. Эти дискуссии возобновились в середине XX в., когда бурное развитие вычислительной техники наполнило методы вычислительной математики новым смыслом. Таким образом, главный пафос исследований прошлого века в этом аспекте сводился к проблеме отнесения математического моделирования, вычислительных математических схем и компьютерных алгоритмов к сфере математической культуры. Оппонентам подобного включения являлись сторонники «чистой» математики», чьи голоса стали слышаться все тише и тише и постепенно сходят на нет. Тем не менее в проблеме содержания и в особенности выбора механизмов диагностирования уровня математической культуры остаются дискуссионные вопросы, которые необходимо осветить в связи с тематикой настоящего исследования.
Материалы и методы исследования
Определив основной целью настоящей работы исследование методов определения уровня компонентов математической культуры, авторы обратились к изучению источников, включая как философию математики, так и проблемы математической подготовки. Зависимость математики от культурной составляющей проистекает из такой проблемы, как неуниверсальность математической культуры в целом и неуниверсальность математического языка в частности [7]. Проблема неуниверсальности математической культуры также имеет несколько измерений и является полем битвы между «чистыми» математиками и их оппонентами, о которой авторы упомянули выше.
К условно первому измерению неуниверсальности авторы относят коллизию между так называемой «математикой с большой буквы» и «математикой с маленькой буквы» [8]. Под первой из них Б.Л. Яшин понимает «чистую», платоновскую, идеальную математику, которую преподают в классических университетах. Под «второй» математикой этот же автор подразумевает так называемую «бытовую» математику, в которой нет места линейным пространствам и «языку ε – δ» [9]. Эта «вторая» математика позволяет людям существовать и функционировать, не чувствуя своей «ущербности», в том числе в сфере, связанной с приложениями математики. Авторы начинают рассмотрение проблемы с того, что язык математики действительно труден и для школьников, и для студентов, которые не выпустились из специализированной школы с углубленным изучением математики. А. Боровик говорит о скором разделении школьной подготовки по математике на два потока – больший и меньший. В большем потоке школьники будут изучать только математические азы, поскольку они не предполагают использовать математику в будущей профессиональной деятельности. Напротив, школьники меньшего потока сосредоточатся на глубоком изучении математики и естественных наук как основы фундаментального образования в соответствующих сферах [10]. В более «провокационной» работе Г.С. Айкенхэд обостряет противоречие между гуманистическими ценностными установками основной массы школьников и «антигуманистическими» образцами преподавания школьной математики в платоновском духе [11]. Соответственно, автор дает шанс на существование «чистой» математики только в рамках STEM-образования. Смягченными отголосками этого противопоставления является значительное число исследований, разрабатывающих проблематику дальнейшей диверсификации математических курсов – для инженеров, экономистов и т.д.
Второе дискуссионное положение по тематике неуниверсальности математики высказал О. Шпенглер еще в 1918 г. в первой части своей знаменитой книги «Закат Европы». Оно заключается в утверждении зависимости форм математики от форм породившей ее культуры [12]. Это утверждение потрясло устои «чистой» математики и вызвало вихреобразные возмущения, которые не стихают до сих пор. Одни последователи Шпенглера подкрепляют его мысль свежими примерами, распространяя идею универсальности на все новые и новые этносы. Другие обобщают положение мэтра, выводя его из теории научного плюрализма, которая базируется на идее зависимости форм любой науки от форм соответствующей культуры. Третьи ссылаются на отсутствие общепринятой непротиворечивой концепции культуры, что, естественно, приводит к мысли о невозможности построения единой теории математической культуры. Очень простое, и в то же время элегантное обоснование положению Шпенглера дал Р. Херш. Действительно, если математическое знание производится человеком, значит, оно находится в зависимости от человека, а человек принадлежит той или иной культуре, т.е. математическое знание обусловлено культурой [13]. Оставляя в стороне и этноматематику, и межкультурные аспекты формирования математической культуры, сосредоточимся далее на поисках методов диагностики уровня сформированности математической культуры в вузе.
Результаты исследования и их обсуждение
Диагностировать тот или иной уровень математической культуры школьника/студента/выпускника достаточно сложно. Прежде всего, исследователи отдельно диагностируют компоненты модели математической культуры [14]. Например, для менеджера можно выделить две группы компонентов – структурные (мировоззренческий, методологический, прогностический) и функциональные (ценностный, когнитивный, эмоциональный, аналитический) [15]. Легче всего проверить уровень формирования методологического компонента, т.е. математических знаний, умений, навыков либо компетенций. Шкала уровней в доступных работах имеет эвристический характер: «высокий – средний – низкий». Авторы не нашли в источниках количественных показателей для измерения уровней. В большинстве случаев понятие «уровень математической культуры» заменяется сходным понятием «уровень математической подготовки», эффективные методы диагностики которого хорошо известны. Задача настоящей статьи – указать те тонкие нюансы, трудноуловимые признаки, которые характеризуют именно отличие высокого уровня математической культуры от среднего или низкого. Можно говорить, что высокий уровень математической культуры характеризует именно стиль решения заданий. Вероятно, что при оценке такого неоднозначного и неуниверсального понятия, как «уровень математической культуры» приходится оперировать такими нечёткими, «интуитивными» характеристиками. С одной стороны, это утверждение может вызывать отторжение многих математиков, привыкших к большей определенности, присущей точной науке. С другой стороны, само понятие культуры, относящееся к области гуманитарного знания, предполагает неоднозначность трактовок.
Поэтому авторы начинают с простых примеров заданий и возможных решений студентов, на основании анализа которых преподаватель может сделать вывод об уровне их математической культуры. Обобщения этих примеров позволят сформулировать некоторые принципы оценки уровня математической культуры студентов.
Пример 1. Учащийся явно демонстрирует низкий уровень математической культуры, если он не меняет знак, раскрывая скобки с минусом перед ними:
.
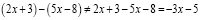В то время как правильное решение:
.
Пример 2. Действия студента с низким уровнем математической культуры при преобразовании иррациональных выражений:
.
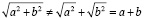Или на численном примере:
.
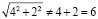Правильное решение:
= 
.
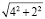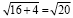Пример 3. Преобразуя дроби, студенты обычно знают правило:
.
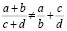Но, производя вычисления, студенты с низким уровнем математической культуры не могут применить это правило, например:
.
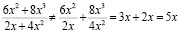В то время как правильный ответ:
.
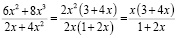Последний ответ не такой «красивый», как предыдущий. С точки зрения студентов с низким уровнем математической культуры, ответы должны быть «красивыми» и короткими. Вариация действий студента с низким уровнем математической культуры в последнем случае может быть и такой:
.
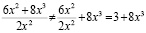В данном случае студент помнит указанное правило, но не может применить его правильно, трактуя его излишне расширительно. Правильный ответ:
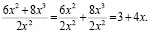
Перейдем к примерам из университетского курса математики.
Пример 4. При нахождении предела
.
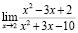Студент с низким уровнем математической культуры вспомнит школьное правило «На ноль делить нельзя» и скажет, что решений нет (предел не существует). В то же время студент со средним (высоким) уровнем культуры раскроет неопределенное выражение и найдет правильный ответ 1/7.
Пример 5. При вычислении производных только студенты с крайне низким уровнем математической культуры делают так: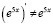 
. В основном студенты правильно помнят правила дифференцирования: 
.
Но уже при решении задания с отрицательным показателем многие студенты с низким уровнем математической культуры выбирают неверный путь: 
. Правильное решение: 
.
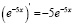Если рассматривать проблему оценки уровня в целом, то ошибки в операциях с дробями и отрицательными величинами являются самыми надежными индикаторами низкого уровня математической культуры.
Пример 6. Такую же ошибку, но более часто демонстрируют студенты с низким уровнем математической культуры, интегрируя:
.
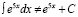Правильное решение:
.
Пример 7. В более сложном случае нахождения определенного интеграла
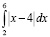
студент с низким уровнем математической культуры вычислит его так:
Студент со средним (скорее, высоким) уровнем культуры раскроет модуль верно и разобьет интеграл на сумму двух интегралов
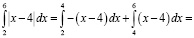
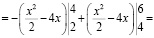
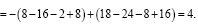
Пример 8. При решении задачи по теории вероятности студент с низким уровнем математической культуры может получить ответ р = 1,35, или р = –0,87, поскольку не может связать аксиоматику теории вероятностей (0 ≤ р ≤ 1) с решением конкретной задачи.
Пример 9. При решении задачи по теории вероятностей или по математической статистике студент с низким уровнем математической культуры может получить распределение дискретной случайной величины в виде
|
xi |
1 |
2 |
3 |
4 |
|
pi |
0.1 |
0.3 |
0.5 |
0.2 |
Однако здесь нарушено условие полноты или нормировки:
.
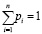В данном случае
.
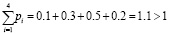Гораздо труднее диагностировать отличия студентов среднего и высокого уровня математической культуры.
Пример 10. Рассмотрим снова Пример 2. Студент со средним уровнем математической культуры сделает так:
=
.
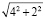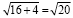Студент же с высоким уровнем математической культуры может придать ответу законченный вид:
=
= 
.
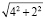Пример 11. При преобразовании иррациональных выражений студент со средним уровнем математической культуры остановится на такой форме правильного ответа:
.
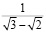Студент с высоким уровнем математической культуры проведет преобразования дальше, избавившись от иррационального выражения в знаменателе:
= 
.
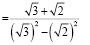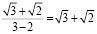Вновь перейдем к примерам из университетского курса математики.
Пример 12. При решении квадратного уравнения, встречающегося, например, в разделе «Дифференциальные уравнения» x2 – 2x + 10 = 0, студент находит корни:
.
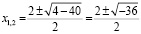Студент со средним уровнем математической культуры делает вывод, что корней нет, поскольку он знает из курса математики средней школы, что извлекать корни из отрицательных чисел нельзя. Студент с высоким уровнем математической культуры знает о существовании комплексных чисел и пишет ответ:
.
Возможно, что многие коллеги не согласятся с авторами, считая, что отсутствие знаний о комплексных числах автоматически присваивает студенту низкий уровень математической культуры. Скорее, здесь может идти речь о недостаточном уровне математической подготовки. Такие же рассуждения применимы к заданиям на действия с матрицами, нахождение пределов, производных, дифференциалов, интегралов, определение сходимости и рядов.
Пример 13. Студент низкого (среднего) уровня математической культуры к задаче «Найти определитель матрицы В = 3A, где А – квадратная матрица размера 3 на 3, если определитель матрицы А равен 2» даст ответ 6.
Студент высокого (среднего) уровня математической культуры знает, что при умножении матрицы на число надо каждый элемент умножить на 3. А при вычислении определителя надо выносить общий множитель элементов одной строки за знак определителя. Таким образом, ответ будет 33 ∙ 2 = 54.
Пример 14. Студент низкого (среднего) уровня математической культуры получит
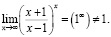
Студент со средним (высоким) уровнем математической культуры знает, что (1∞) представляет собой неопределенное выражение, и будет делать преобразования:
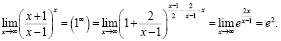
Пример 15. Студент среднего уровня математической культуры, находя производную от функции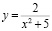 
, использует правило дифференцирования частного:
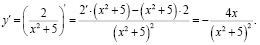
Студент высокого уровня математической культуры увидит сложную функцию
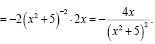
Пример 16. В задании на нахождение дифференциала функции y = 3x2 + 2x в точке 2 студент со средним (низким) уровнем математической культуры может дать ответ dy = 14, а студент с высоким (средним) уровнем математической культуры напишет dy = 14dx.
Пример 17. Студент со средним уровнем математической культуры вычисляет определенный интеграл следующим образом
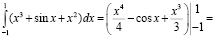
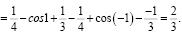
Студент с высоким уровнем математической культуры воспользуется свойствами интеграла от четных и нечетных функций по симметричному промежутку и возьмет интеграл так:
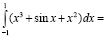
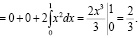
Пример 18. Студент низкого (среднего) уровня математической культуры, решая дифференциальное уравнение с разделяющимися переменными y’ = y2, получит общее решение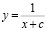 
. Студент высокого уровня математической культуры увидит особое решение y = 0, которое было потеряно при делении на y2.
Пример 19. Исследуя сходимость ряда
,
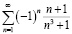студент со средним (низким) уровнем математической культуры может дать ответ: «ряд сходится», в то время как студент с высоким (средним) уровнем математической культуры обязательно уточнит: «ряд сходится абсолютно».
Рассмотренные примеры показывают, что оценить низкий уровень математической культуры студентов достаточно просто: студент либо не знает правил математики, либо не может их применить. Оценка среднего и высокого уровней математической культуры является более сложной. Всегда ли ошибка говорит о низкой математической культуре? Возможно, эта ошибка появилась случайно, например, по причине плохого самочувствия или стресса студента. Всегда ли средний уровень математической культуры означает, что студент может дать правильные ответы? Действительно ли обладающий высоким уровнем математической культуры студент выберет наиболее рациональные способы решения, получит ответ в законченной форме? Можно предложить использовать для оценки уровня математической культуры задания, предлагающие испытуемому не решить пример, а провести рассуждение. Например, «поясните, почему в задаче… ответ… является неверным, не производя вычислений». Студенты высокого и среднего уровня математической культуры, даже сделав вычислительную ошибку, могут ее увидеть и исправить, поняв, что результат не соответствует действительности. Например, для определения среднего уровня математической культуры, можно использовать примеры, аналогичные по сути Примеру 9.
Примеры 20–23. Когда ищут расстояние от точки до прямой или вычисляют площадь фигуры, результат не может быть отрицательным. В вероятностных задачах дисперсия не может быть отрицательной, модуль коэффициента корреляции не может превышать 1.
Для выявления высокого уровня математической культуры необходимы более тонкие примеры, анализируя которые студент замечает не самые очевидные ошибки.
Пример 24. При вычислении определенного интеграла студент получает отрицательный результат. Это не нахождение площади, но студент видит, что под интегралом стоит неотрицательная функция, а порядок пределов интегрирования нормальный. В этом случае студент понимает, что интеграл отрицательным быть не может. После этого находит и исправляет вычислительную ошибку.
Пример 25. Вычислить математическое ожидание случайной величины
|
xi |
-2 |
0 |
3 |
5 |
|
pi |
0,5 |
0,1 |
0,1 |
0,3 |
Допустим, совершив вычислительную ошибку, студент получил ответ М(X) = 5,2. Студент с высоким уровнем заметит, что этот ответ неверный, так как математическое ожидание не может быть больше максимального значения самой случайной величины или меньше минимального.
Отсюда следует важный вывод по методике оценки уровня математической культуры студента. Во-первых, эта оценка превращается в протяженный по времени процесс. Во-вторых, скорее всего процедура оценки будет двухступенчатой: на первом этапе отсеиваются студенты с низким уровнем математической культуры, на втором – разделяются студенты среднего и высокого уровней. Если рассматривать оценку уровня математической культуры как основание для дифференциации студентов в целях персонализации подготовки, то становится понятно, что объективные результаты можно получить только при реализации схемы обучения «2+2» (или «2+2+2» при сохранении института магистратуры в отечественной высшей школе). Согласно этому подходу, первые два года все студенты одной группы направлений обучаются по единой программе, а на третьем курсе начинается разделение по направлениям в соответствии со склонностью студентов к практической инженерной или исследовательской деятельности. При этом технология математической подготовки диверсифицируется в соответствии с результатами входного тестирования по математике, основанного на оценке уровня математической подготовки. А вот дифференциация в конце второго года обучения уже должна учитывать именно уровень математической культуры, склонность к самостоятельной познавательной деятельности, проявления творческого подхода к решению задач.
Заключение
Очевидно, что оценка уровня математической культуры студента существенно зависит от оценивающего, т.е. этот процесс является субъективным. Для объективизации оценки уровня математической культуры сообщество математиков должно выработать критерии дифференциации и оценочные средства. В связи с повышением значимости математической подготовки в условиях четвертой промышленной революции и развития STEM-образования такая потребность общества появляется. На основании оценки уровня математической культуры и других характеристик обучаемых можно провести дифференциацию подготовки студентов начиная с третьего курса, что будет существенным вкладом в реализацию идеи персонализации обучения в вузе.
Библиографическая ссылка
Вагурина И.В., Краснощеков В.В., Семенова Н.В. ОБ УРОВНЕ МАТЕМАТИЧЕСКОЙ ПОДГОТОВКИ И МАТЕМАТИЧЕСКОЙ КУЛЬТУРЫ СТУДЕНТОВ УНИВЕРСИТЕТОВ // Современные наукоемкие технологии. – 2022. – № 12-1. – С. 104-110;URL: https://top-technologies.ru/ru/article/view?id=39445 (дата обращения: 25.04.2024).