Жизнь современного человека тесно связана с различными цифровыми устройствами, элементами которых являются дискретные объекты (ДО). Важным этапом производства ДО является обнаружение и исправление дефектов, которое называется диагностированием.
Одним из основных понятий в диагностировании, где определяется исправность объекта, является понятие алгоритма диагностирования.
«Алгоритм диагностирования (АД) – это совокупность предписаний о проведении диагностирования. Он устанавливает состав и порядок проведения так называемых элементарных проверок» – определение из учебника С.М. Бородина «Основы технической диагностики электронных средств» [1].
Автором работы [2] отмечается: «C каждым днем происходит бурное усложнение процессов на автоматизированных системах управления, на сегодняшний день невозможно обойтись без использования контрольно-измерительных приборов. В основном используются дискретные устройства (цифровые устройства)».
Основной причиной параллелизма является «сокращение времени вычисления алгоритма. Поэтому для анализа эффективности алгоритмов диагностирования важна оценка времени выполнения алгоритма» [3]. Работы многих авторов уделяются распараллеливанию алгоритмов, которые базируются на математических методах параллельных вычислений. Например, авторы работ [3, 4] рассматривают методы и средства параллельных вычислений.
Исследованию методов тестирования и диагностирования компьютерных систем посвящена работа [5]. В ней говорится, что одним из способов «борьбы с неисправностями компонентов автоматизированных систем» являются «диагностические процедуры, позволяющие обнаруживать неисправность».
А в работе [6] автор рассмотрел множество алгоритмов диагностирования дискретных объектов. «В это множество входят алгоритмы-процедуры, которые являются элементами этого множества: например, к элементам множества относятся параллельная процедура с повторными запусками теста, параллельная процедура с продолжением теста, параллельная процедура с неполными возвратами теста, ν-процедура, ν-процедура с неполными возвратами теста и другие. Каждый алгоритм-процедура диагностирования дискретных объектов описывается аналитической формулой, которая вычисляет суммарные временные затраты» [6]. Автором было доказано, что параллельные алгоритмы имеют выигрыш в суммарных временных затратах (СВЗ) в отличие от последовательных алгоритмов диагностирования.
При параллельном диагностировании одновременно подается тест длиной T. Тест подается в некоторое множество дискретных объектов, и сравниваются выходные сигналы с идентичными выходами «с целью вычисления функции неравнозначности (ФН)» [6].
Выше сообщалось, что в процессе диагностирования группы однотипных ДО параллельная и v-процедура, позволяет повысить быстродействие [6, 7].
Цель исследования – описать новый алгоритм диагностирования дискретных объектов и доказать, что новый алгоритм является более выигрышным в СВЗ, чем параллельные алгоритмы-процедуры диагностирования ДО. Новый алгоритм назовем обратным алгоритмом.
Для того чтобы доказать, что обратный алгоритм имеет выигрыш по сравнению с параллельной и ν-процедурой диагностирования ДО, приведем примеры.
Сравним обратный алгоритм с параллельной процедурой поиска дефектов с реверсированием теста.
Пусть диагностируется три ДО (N = 3), с разными дефектами μ1 = 4 – количество дефектов первого объекта, μ2 = 2 – количество дефектов первого объекта, μ3 = 6 – количество дефектов первого объекта. Длина теста T = 200, t0 и tk – начальный и конечный векторы теста соответственно. Пусть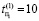 
, 
, 
, 
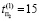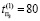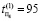– время поиска дефектов в первом объекте, 
, 
, 
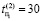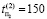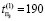– время поиска дефектов в первом объекте, 
, 
, 
, 
, 
, 
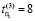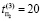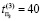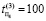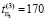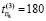– время поиска дефектов в первом объекте.
Временная диаграмма параллельной процедуры изображена на рис. 1. На основании рисунка имеем следующее аналитическое выражение [6]:
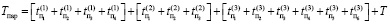
или, в общем виде,
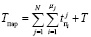, (1)
где обозначили N – количество объектов,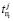 
– время поиска i-го дефекта в j объекте, μ – количество дефектов в ДО. Следовательно, согласно полученной формуле (1)
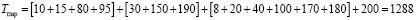
условных единиц.
Временная диаграмма обратной параллельной процедуры представлена на рис. 2.
Согласно рис. 2 сначала тест подается одновременно на несколько ДО, в примере три ДО, и после того, как был обнаружен первый дефект в каждом объекте, через время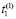 
, 
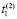, tk, возвращается в состояние t0. После того, как был устранен обнаруженный первый дефект, тест запускается в обратном порядке (рис. 2), в отличие от параллельного, который повторяется заново (рис. 1).
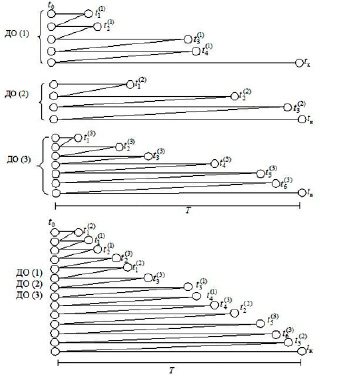
Рис. 1. Временная диаграмма параллельной процедуры поиска дефектов с реверсированием теста (N = 3, μ1 = 4, μ2 = 2, μ3 = 6)
Основываясь на рис. 2, СВЗ для обратного алгоритма-процедуры диагностирования трех объектов определяются с помощью выражения
Тобрат.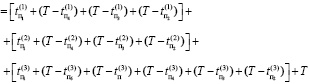 
Тобрат.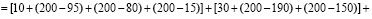 
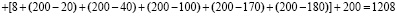
условных единиц или, в общем виде,
Тобрат.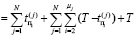 
. (2)
_fmt.jpeg)
_fmt.jpeg)
Рис. 2. Временная диаграмма обратного алгоритма диагностирования ДО (N = 3, μ1 = 4, μ2 = 2, μ3 = 6)
Очевидно, что имеет выигрыш обратный алгоритм по сравнению с параллельным алгоритмом и составляет
w = 1288 / 1208 = 1.07,
в общем виде:
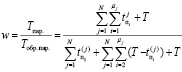. (3)
Во временной диаграмме (рис. 2) обратного алгоритма заметим, что чем больше дефектов обнаруживаются во второй половине теста, тем меньше СВЗ, то есть чем меньше величина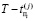 
.
Итак, число всех обнаруживаемых дефектов μ можно разбить на два подмножества:
− μ1 – множество дефектов, обнаруженных в первой половине теста;
− μ2 – множество дефектов, обнаруженных во второй половине теста;
Пусть tсредμ1 = Т / 4 – это среднее время обнаружения всех дефектов подмножества μ1, tсредμ2 = 3Т / 4 – среднее время подмножества μ2. Тогда формулу (3) можно преобразовать:
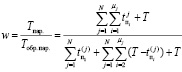. (4)
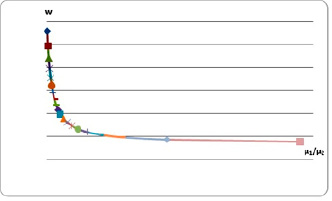
Рис. 3. Изменение коэффициента соотношения w между СВЗ параллельной процедуры диагностирования ДО и СВЗ при обратном алгоритме параллельного алгоритма в зависимости от величины
Графически w представлен на рис. 3. График показывает соответствие w между СВЗ параллельной процедуры и СВЗ при обратном алгоритме параллельной процедуры с реверсом в зависимости от величины μ1 / μ2. То есть соответствие между μ1 и μ2, при этом длина теста T = 100, количество обнаруживаемых дефектов μ = 20,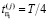 
, а N = 5 – число ДО.
Анализируя график рис. 3, можно сделать выводы о том, что обратный алгоритм параллельной процедуры обнаружения дефектов в дискретных объектах:
1. Имеет выигрыш в СВЗ по сравнению с параллельным алгоритмом, когда μ2 > μ1.
2. При μ2 = μ1 алгоритмы с точки зрения временных затрат адекватны.
3. При μ2 < μ1 применение обратного алгоритма неэффективно, то есть не имеет выигрыша в СВЗ.
Таким образом, обратный алгоритм параллельной процедуры поиска дефектов с реверсированием теста эффективно применять, когда число обнаруживаемых дефектов больше в конце теста, а не в начале теста.
Сравним обратный алгоритм с ν-процедурой поиска дефектов с реверсированием теста.
Пусть даны три ДО (N = 3 – количество объектов) с одинаковым количеством дефектов μ2 = μ1 = 2, длина теста T = 30, t0 и tk – начальный и конечный векторы теста соответственно,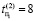 
, 
, 
, 
, 
, 
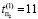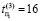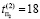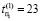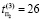, где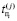 
– время поиска i-го дефекта в j-м ДО, 
, 
.
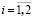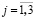Временная диаграмма для ν-процедуры, которая может быть интерпретирована как ориентированный граф, вершины которого соответствуют состояниям ДО в моменты обнаружения дефектов, а на дугах задана числовая функция значений времен поиска обнаруженного дефекта, приведена на рис. 4.
Суммарные временные затраты (СВЗ), на поиск всех дефектов в ДО по ν-процедуры, в соответствии с формулой (1):
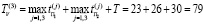
где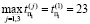 
– максимальное время поиска 1-х дефектов
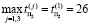– максимальное время поиска 2-х дефектов
Временная диаграмма обратной алгоритма ν-процедуры показана на рис. 5. Из рисунка видно, что, в отличие от ν-процедуры, тест на ДО подается в обратном порядке, и после обнаружения первых дефектов во всех трех ДО, через время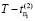 
(это максимальное время поиска дефекта), реверсируется в исходное состояние t0 (рис. 5). После устранения обнаруженного дефекта тест также подается в обратном направлении и также после обнаружения дефектов реверсируется в исходное состояние t0, через время 
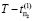. Последний прогон теста из состояния tк в t0, на котором не обнаруживается ни одного дефекта, свидетельствует об исправности ДО.
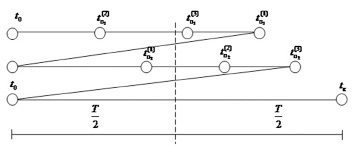
Рис. 4. Временная диаграмма ν-процедуры с реверсом обнаружения дефектов (N = 3,μ = 2)
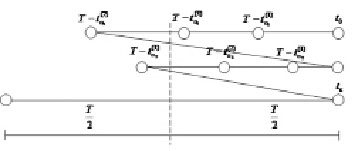
Рис. 5. Временная диаграмма обратной процедуры диагностирования поиска дефектов (N = 3,μ = 2)
Суммарные временные затраты обратного алгоритма, согласно рис. 5 получим выражение
.
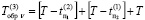Заметим, что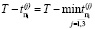 
.
Следовательно, для вычисления суммарных временных затрат обратного алгоритма используем следующую формулу:
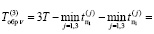
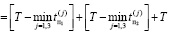. (5)
Согласно формуле (5) суммарные временные затраты обратного алгоритма
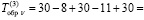
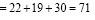у.е.
Соответственно, выигрыш во времени от применения обратного алгоритма по сравнению с v-процедурой:
w = 79 / 71 = 1,11 у.е.
В общем виде:
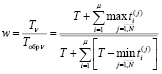. (6)
Найдем предел w между временными затратами при v-процедуре и временными затратами при обратном алгоритме. Пусть max t, min t → T
.
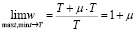Предел w равен 1 + μ, т.е. выигрыш от применения обратного алгоритма по сравнению с v-процедурой всегда есть.
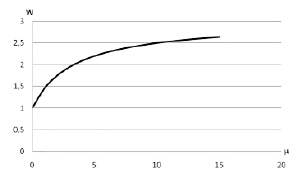
Рис. 6. Выигрыш обратного алгоритма по сравнению с v-процедурой
На риc. 6 построен график w в зависимости от количества дефектов.
Как показывает график рис. 6, обратный алгоритм обнаружения дефектов в ДО обеспечивает выигрыш, когда дефекты обнаруживаются в конце теста. Поэтому если дефекты обнаруживаются во второй половине теста, то использование обратного алгоритма поиска дефектов является эффективнее ν-процедуры поиска дефектов с реверсированием теста.
Таким образом, новый алгоритм более эффективный по сравнению с параллельной процедурой и ν-процедурой поиска дефектов с реверсированием теста, когда число дефектов, обнаруживаемых во второй половине теста, больше числа дефектов, обнаруживаемых в первой половине теста. Поэтому обратный алгоритм более эффективен, чем параллельная процедура и ν-процедура, то есть имеет наименьший СВЗ, когда наибольшее число дефектов обнаруживается в конце теста.
Библиографическая ссылка
Тюлюш С.Т. ОБРАТНЫЙ АЛГОРИТМ ПАРАЛЛЕЛЬНЫХ ПРОЦЕДУР ДИАГНОСТИРОВАНИЯ ДИСКРЕТНЫХ ОБЪЕКТОВ // Современные наукоемкие технологии. – 2022. – № 12-1. – С. 69-75;URL: https://top-technologies.ru/ru/article/view?id=39439 (дата обращения: 23.04.2024).