Вольфрам является уникальным металлом для создания нагревательных и осветительных приборов различного назначения. Поэтому определение его температуры в различных режимах работы приборов, в зависимости от изменения условий окружающей среды, напряжения питания является актуальной задачей. Температура определяет твердость, прочность, износостойкость, расширение, скорость испарения и другие параметры. Вольфрам является одним из основных металлов, используемых на температурах свыше 1000 °C. Следует учитывать, что на высоких значениях температуры в наибольшей степени проявляется ее влияние на параметры всех веществ.
При проектировании приборов на основе вольфрамовой проволоки установление величины ее температуры возможно по известной зависимости температуры от величины изменения удельного электрического сопротивления. В литературных источниках эта зависимость приводится в виде таблицы [1, 2]. Величине температуры сопоставляется отношение величины удельного электрического сопротивления вольфрама к сопротивлению при 300 К (R300). В приводимых источниках шаг изменения температуры обычно равен 100 К.
Также известна аналитическая зависимость сопротивления металлов от температуры в виде [3, 4]:
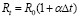 , (1)
, (1)
где Rt – сопротивление металла при температуре t; R0 – сопротивление при начальной температуре; α – температурный коэффициент сопротивления; Δ t – величина изменения температуры металла.
Зависимость (1) позволяет по известному начальному электрическому сопротивлению (для вольфрама эта величина равна 300 К) и температурному коэффициенту (для вольфрама 0,0046 К-1) рассчитывать сопротивление Rt для требуемой температуры и, соответственно, по табличным данным определять ее. Следует учитывать, что изменение электрического сопротивления вольфрамовой проволоки, определенное по (1), линейно.
Предлагается сравнить несколько аналитических зависимостей, которые можно будет использовать для расчета величины температуры вольфрамовой проволоки по величине изменения электрического сопротивления. Полученные результаты также сравниваются с результатами измерений электрического сопротивления тела накала ламп.
Материалы и методы исследования
По известным данным в табличном редакторе Excel построен график изменения температуры от изменения удельного электрического сопротивления. Табличный редактор позволяет по графику строить различные линии тренда, соответствующие экспериментальным результатам [5]. Выбраны четыре аналитические зависимости величины температуры t от изменения удельного электрического сопротивления вольфрамовой проволоки Rt / R300:
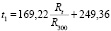 , (2)
, (2)
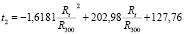 , (3)
, (3)
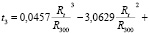
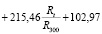 , (4)
, (4)
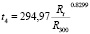 . (5)
. (5)
Зависимость (2) является линейной функцией, (3) и (4) – полиномы второго и третьего порядка, (5) – степенная функция.
В табл. 1 приводятся известные экспериментальные данные зависимости температуры t от изменения сопротивления вольфрамовой проволоки Rt / R300 и соответствующие им величины t1, t2, t3, t4, полученные с помощью (2)–(5).
В таблице также приводятся соответствующие относительные погрешности d1, d2, d3, d4 описания экспериментальных данных предложенными функциями.
Наибольшее дифференциальное отклонение имеет линейная функция, наименьшее – степенная функция. Из расчетных данных следует, что величины расхождений для линейной функции наибольшие для всех точек аппроксимации экспериментальных данных. Для вольфрама использование (1) при определении изменения сопротивления от температуры приводит к появлению больших отклонений.
Интегральная оценка погрешности по диапазону изменения температур от 300 до 3600 К соответствует для (2) – 138,19 %, (3) – 24,86 %, (4) – 13,39 %, (5) – 16,44 %. Анализ величин отклонений также показывает меньшие расхождения описания полиномом третьего порядка в диапазоне температур выше 800 К.
Следовательно, рекомендуется для оценки температур использовать полиномиальную зависимость третьего порядка.
Широкое развитие вычислительной техники, на которой установлены программные средства (Excel, Access), реализующие полиномиальную функцию третьего порядка, позволяют автоматизировать расчет необходимого значения температуры [6].
Выражение (4) позволяет определять температуру в произвольном режиме работы приборов с вольфрамовыми спиралями, даже в тех случаях, когда измерение невозможно с помощью специализированных измерительных приборов (пирометров).
Измерение значения Rt и заранее известное значение R300 при работе прибора позволяет определять искомое значение температуры.
Получение экспериментальных результатов измерений электрического сопротивления вольфрама, особенно на высоких температурах, является сложной задачей. Необходимо обеспечить изоляцию проволоки от воздействия внешней среды. Нагрев до высоких значений температуры приводит к ее разрушению.
Наиболее простым решением является измерение сопротивления вольфрамовой проволоки, являющейся телом накала тепловых источников света [7]. К вольфрамовым спиралям ламп предъявляются высокие требования по качеству материала, малому содержанию примесей, по отсутствию механических повреждений, наличию расслоя, трещин, пор способных вызывать локальные перегревы.
Таблица 1
Зависимость величины температуры вольфрама от изменения удельного электрического сопротивления
|
Rt / R300 |
t |
Результат расчета |
|||||||
|
t1 |
δ1 |
t2 |
δ2 |
t3 |
t3 |
t4 |
δ4 |
||
|
1,00 |
300 |
418,58 |
39,53 |
329,12 |
9,71 |
315,41 |
5,14 |
294,97 |
1,68 |
|
1,43 |
400 |
491,34 |
22,84 |
414,71 |
3,68 |
404,95 |
1,24 |
396,91 |
0,77 |
|
1,87 |
500 |
565,80 |
13,16 |
501,67 |
0,33 |
495,47 |
0,91 |
495,88 |
0,82 |
|
2,34 |
600 |
645,33 |
7,56 |
593,87 |
1,02 |
590,96 |
1,51 |
597,30 |
0,45 |
|
2,85 |
700 |
731,64 |
4,52 |
693,11 |
0,98 |
693,21 |
0,97 |
703,48 |
0,50 |
|
3,36 |
800 |
817,94 |
2,24 |
791,51 |
1,06 |
794,07 |
0,74 |
806,47 |
0,81 |
|
3,88 |
900 |
905,93 |
0,66 |
890,96 |
1,00 |
895,51 |
0,50 |
908,76 |
0,97 |
|
4,41 |
1000 |
995,62 |
0,44 |
991,43 |
0,86 |
997,50 |
0,25 |
1010,64 |
1,06 |
|
4,95 |
1100 |
1087,00 |
1,18 |
1092,86 |
0,65 |
1099,99 |
0,00 |
1112,32 |
1,12 |
|
5,48 |
1200 |
1176,69 |
1,94 |
1191,50 |
0,71 |
1199,23 |
0,06 |
1210,30 |
0,86 |
|
6,03 |
1300 |
1269,76 |
2,33 |
1292,89 |
0,55 |
1300,84 |
0,06 |
1310,28 |
0,79 |
|
6,58 |
1400 |
1362,83 |
2,66 |
1393,31 |
0,48 |
1401,10 |
0,08 |
1408,72 |
0,62 |
|
7,14 |
1500 |
1457,59 |
2,83 |
1494,55 |
0,36 |
1501,84 |
0,12 |
1507,52 |
0,50 |
|
7,71 |
1600 |
1554,05 |
2,87 |
1596,55 |
0,22 |
1603,04 |
0,19 |
1606,74 |
0,42 |
|
8,28 |
1700 |
1650,50 |
2,91 |
1697,50 |
0,15 |
1702,93 |
0,17 |
1704,71 |
0,28 |
|
8,86 |
1800 |
1748,65 |
2,85 |
1799,14 |
0,05 |
1803,29 |
0,18 |
1803,24 |
0,18 |
|
9,44 |
1900 |
1846,80 |
2,80 |
1899,70 |
0,02 |
1902,41 |
0,13 |
1900,67 |
0,04 |
|
10,03 |
2000 |
1946,64 |
2,67 |
2000,87 |
0,04 |
2002,02 |
0,10 |
1998,75 |
0,06 |
|
10,63 |
2100 |
2048,17 |
2,47 |
2102,60 |
0,12 |
2102,10 |
0,10 |
2097,48 |
0,12 |
|
11,24 |
2200 |
2151,39 |
2,21 |
2204,83 |
0,22 |
2202,68 |
0,12 |
2196,89 |
0,14 |
|
11,84 |
2300 |
2252,92 |
2,05 |
2304,21 |
0,18 |
2300,49 |
0,02 |
2293,78 |
0,27 |
|
12,46 |
2400 |
2357,84 |
1,76 |
2405,68 |
0,24 |
2400,49 |
0,02 |
2393,03 |
0,29 |
|
13,08 |
2500 |
2462,76 |
1,49 |
2505,90 |
0,24 |
2499,43 |
0,02 |
2491,44 |
0,34 |
|
13,72 |
2600 |
2571,06 |
1,11 |
2608,06 |
0,31 |
2600,55 |
0,02 |
2592,20 |
0,30 |
|
14,34 |
2700 |
2675,97 |
0,89 |
2705,75 |
0,21 |
2697,59 |
0,09 |
2689,04 |
0,41 |
|
14,99 |
2800 |
2785,97 |
0,50 |
2806,84 |
0,24 |
2798,41 |
0,06 |
2789,82 |
0,36 |
|
15,63 |
2900 |
2894,27 |
0,20 |
2905,04 |
0,17 |
2896,85 |
0,11 |
2888,31 |
0,40 |
|
16,29 |
3000 |
3005,95 |
0,20 |
3004,92 |
0,16 |
2997,58 |
0,08 |
2989,17 |
0,36 |
|
16,95 |
3100 |
3117,64 |
0,57 |
3103,39 |
0,11 |
3097,59 |
0,08 |
3089,34 |
0,34 |
|
17,62 |
3200 |
3231,02 |
0,97 |
3201,91 |
0,06 |
3198,45 |
0,05 |
3190,35 |
0,30 |
|
18,28 |
3300 |
3342,70 |
1,29 |
3297,53 |
0,07 |
3297,24 |
0,08 |
3289,21 |
0,33 |
|
18,97 |
3400 |
3459,46 |
1,75 |
3396,00 |
0,12 |
3400,00 |
0,00 |
3391,92 |
0,24 |
|
19,66 |
3500 |
3576,23 |
2,18 |
3492,93 |
0,20 |
3502,32 |
0,07 |
3494,00 |
0,17 |
|
20,35 |
3600 |
3692,99 |
2,58 |
3588,31 |
0,32 |
3604,30 |
0,12 |
3595,47 |
0,13 |
В качестве объекта измерений предлагается использовать серийно выпускаемые лампы, в которых вольфрамовое тело накала располагается в вакууме или атмосфере инертного газа.
При использовании бытовых ламп температура стеклянной колбы значительно меньше температуры вольфрамовой спирали. В качестве ламп использовались вакуумные лампы типа В220-230-25 и газополные Б220-230-25. Мощность ламп составляет 25 Вт, что упрощает требования к используемому оборудованию.
Измерение сопротивления осуществляется на экспериментальной установке, схема которой приведена на рисунке.
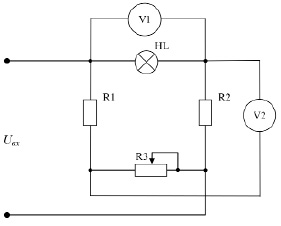
Схема для измерения сопротивления тела накала ламп
Для обеспечения высокой точности измерений лампа HL включается в одно из плеч моста. Температура тела накала лампы изменяется регулированием подаваемого на вход электрической схемы напряжения Uвх. Величина напряжения, прикладываемого к источнику света при этом, регистрируется вольтметром V1. Уровень напряжения на лампе будет определять величину температуры тела накала.
При измерениях устанавливается баланс плеч моста после изменения прикладываемого входного напряжения, определяемый по нулевым показаниям вольтметра V2. Уравновешивание моста достигается изменением сопротивления R3. Сопротивление лампы при этом вычисляется по формуле
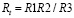 . (6)
. (6)
Сопротивление и изменение сопротивления токоведущей арматуры лампы при измерениях не учитывалось, поскольку их величины на несколько порядков меньше соответствующих величин вольфрамовой спирали.
При проведении измерений необходимо учитывать большую величину протекающего тока по лампе и большую мощность, выделяемую на резисторе в соседней ветви моста.
В схеме используется реостат РПШ-0,6, магазин сопротивлений Р33, магазин сопротивлений МСР 58, вольтметр В7-26. Питание схемы для более высокой точности измерений осуществлялось постоянным напряжением от регулируемого источника.
Результаты исследования и их обсуждение
В табл. 2 представлены измеренные значения электрического сопротивления ламп типа В220-230-25 и Б220-230-25 при различных величинах прикладываемого напряжения.
В табл. 2 также приводятся рассчитанные по (4) величины температур вольфрамовой спирали, соответствующие измеренным значениям сопротивлений и рассчитанным отношениям Rt / R300.
Для указанных типов ламп температуру тела накала можно определять по величине напряжения на них. Следует отметить, что по результатам измерений температура вольфрамовой спирали газополных ламп имеет большее значение. Это определяет их большую световую отдачу при одинаковых значениях прикладываемого напряжения.
Сравнение измеренных величин сопротивлений и рассчитанных отношений Rt / R300 с известными данными показывает их соответствие. Например, измеренное отношение Rt / R300 ламп В220-230-25 для температуры 1406 К равно 6,61 (известная аналогичная величина для 1400 К равна 6,58), для 1702 К равно 8,28 (известная аналогичная величина для 1700 К равна 8,28). Лампы Б220-230-25 при 1094 К имеют отношение Rt / R300 равное 4,92 (известная аналогичная величина для 1100 К равна 4,95), при 1912 К равное 9,5 (известная аналогичная величина для 1900 К равна 9,44).
Таблица 2
Зависимость электрического сопротивления и температуры тела накала ламп от напряжения
|
U, В |
В220-230-25 |
Б220-230-25 |
||||
|
Rt, Ом |
Rt / R300 |
t, K |
Rt, Ом |
Rt / R300 |
t, K |
|
|
0 |
174,1 |
1,00 |
315 |
148,4 |
1,00 |
315 |
|
20 |
760,9 |
4,37 |
989 |
477,8 |
3,22 |
766 |
|
40 |
985,3 |
5,66 |
1232 |
730,5 |
4,92 |
1094 |
|
60 |
1150,3 |
6,61 |
1406 |
964,1 |
6,50 |
1385 |
|
80 |
1317,5 |
7,57 |
1577 |
1125,6 |
7,58 |
1580 |
|
100 |
1441,2 |
8,28 |
1702 |
1280,6 |
8,63 |
1763 |
|
120 |
1544,0 |
8,87 |
1804 |
1409,8 |
9,50 |
1912 |
|
140 |
1634,5 |
9,39 |
1893 |
1528,9 |
10,30 |
2047 |
|
160 |
1761,2 |
10,12 |
2016 |
1637,5 |
11,03 |
2168 |
|
180 |
1842,9 |
10,59 |
2094 |
1732,8 |
11,68 |
2273 |
|
200 |
1917,8 |
11,02 |
2165 |
1818,1 |
12,25 |
2366 |
|
220 |
1990,6 |
11,43 |
2234 |
1887,3 |
12,72 |
2441 |
Заключение
Получена полиномиальная зависимость изменения температуры от изменения величины электрического сопротивления вольфрамовой проволоки. Она позволит определять температуру без использования специализированных средств измерений и проектировать нагревательные и осветительные приборы с учетом полученных значений. Известное линейное изменение электрического сопротивления вольфрама от температуры с использованием температурного коэффициента сопротивления имеет более высокую погрешность, чем полученная функция. Результаты измерений электрического сопротивления вольфрамовой проволоки, являющейся телом накала ламп, также свидетельствуют о возможности использования полученной полиномиальной зависимости.
Библиографическая ссылка
Родин В.В., Толмачева И.И. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ВОЛЬФРАМОВОЙ ПРОВОЛОКИ // Современные наукоемкие технологии. 2022. № 12-1. С. 52-56;URL: https://top-technologies.ru/ru/article/view?id=39436 (дата обращения: 01.02.2026).
DOI: https://doi.org/10.17513/snt.39436



