Киберфизические системы в настоящее время могут быть использованы для решения различных практических проблем. Их можно внедрять в любой организации. Соответствующий набор ресурсов должен быть сформирован для того, чтобы поддерживать их функционирование. Можем использовать понятие многоканальной системы при описании ресурсного обеспечения. Персонал, программное обеспечение оборудование позволяют сформировать ключевые ресурсы [1, 2]. Достаточность обеспечения ресурсами ведет к требуемому уровню обслуживания внутри киберфизических систем. Многоканальная система дает возможности для того, чтобы осуществлять накопление относительно всех ресурсов. Также многоканальные подходы при анализе услуг и структур управления позволяют прийти к эффективному распределению ресурсов [3].
Материалы и методы исследования
В киберфизической системе по ресурсному обеспечению осуществим формализацию с точки зрения структуры модуля. Тогда управление в нем будет рационализироваться (рисунок).
Определить предлагаемый модуль по компонентам ресурсов и управления можно на основе отношений по непустым множествам
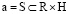. (1)
В ходе моделирования S рассматривается как набор возможных вариантов модуля распределения ресурсов. Учитывается, что R будет множеством компонентов ресурсов [4]. Компоненты управления описываются на основе множества H.
Базовое множество мы представляем следующим образом
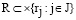. (2)
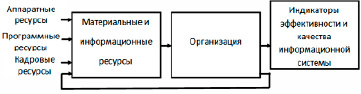
Рис. 1. Иллюстрация структурных особенностей ресурсного обеспечения киберфизической системы на основе многоканального подхода
Ресурс, относящийся к j-му типу, в ходе моделирования рассматривается в виде совокупности вариантов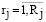 
; ссылка на имена компонентов ресурсов осуществляется на основе набора индексов j; декартово произведение обозначается как ×. В таких случаях можно говорить о справедливости соотношения
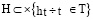. (3)
Управленческий компонент t-типа рассматривается в виде вариантов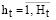 
. Множество T будет связано с индексами, соотносимыми с названиями компонентов управления [5]. Элементы множества (1) могут быть сформированы на основе пары векторов
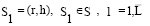. (4)
В ходе моделирования r = (r1 ,...,rj,...,rJ), j =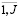 
, rj = 
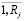, h = (h1 ....,ht,..., hT), t = 
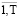, ht = 
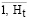. Совместная пара элементов будет обозначаться (rj,ht) = Ug, g = 
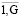. После этого представляем
Sl = (U1,...,Ug,...,UG ), l =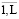 
. (5)
При рассмотрении Ug = 1,Ug, g =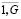 
являются элементами в модуле поддержки ресурсообеспечения. В ходе реализации модуля общее количество вариантов рассматривается как L. В модуле можно дать характеристику элементов Ug при помощи метрического вектора fug. Уровень показателей fug будет оказывать влияние на интегральные показатели эффективности киберфизической системы Fi, i = 
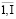. Справедлива следующая зависимость
Fi = Y(fug.). (6)
Значения заданного показателя по всем элементам модуля будут оказывать влияние на соответствующие типы неисправностей внутри киберфизической системы. Ресурсная обеспеченность связана заметным образом с некоторыми показателями Fi. Например, должно быть достаточное количество аппаратного или программного обеспечения. Может быть сформировано подмножество IR ∈ I на основе таких показателей. Другие показатели могут оказывать влияние на управленческую составляющую [6, 7]. Например, специалисты проводят периодическую проверку оборудования. Будет выполняться свойство принадлежности для подмножества IH ∈ I благодаря указанным показателям. В ходе решения задач [8] по модульному управлению можно увидеть связь среди подмножеств IR и IH.
IR ∪ IH = I, IR ∩ IH ≠ ∅. (7)
Перечисленные показатели будут устанавливаться на наборах Ug вследствие использования функций
fug ∈{Ug×f}, Ψi ∈ {sxFi: i∈I}. (8)
По зависимости (8) имеются возможности для вычисления значений функций с привлечением соответствующей комбинации s элементов Ug. В таком случае это можно представлять таким образом: Fi(s(Ug),fug). Формируются зависимости (8), по работе киберфизической системы происходит реализация статистической обработки информации. Показатели элементов модуля будут описываться на основе случайных величин Fug. Стохастическим образом будут описываться показатели Fi = yi(Fug). Вероятностные меры могут быть по ним заданы соответствующим образом:
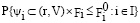. (9)
В ходе моделирования P{} рассматривается в виде вероятности. Искомое значение по показателю Fi будет F0i. Когда происходит процесс управления киберфизической системой, тогда будет жестким образом определение ресурсного обеспечения rg0∈Ug , g =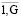 
. Относительно hg0 проведение выбора будет при условии
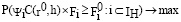. (10)
Следующее выражение может быть использовано для выбора элементов rg0, hg0, если реализуется управление модулем:
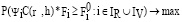. (11)
Вероятность выбора по показателям Fi(iÎIR), когда используется система соотношений (8), рассматривается таким образом
.
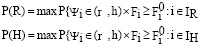При учете правила (10) в виде вероятности выбора анализируется такая величина pтp. При учете правила (11) как вероятность выбора анализируется величина Pc. Можно сделать такую запись условий при учете формирования подмножеств IR, IH :
.
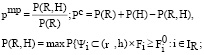
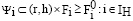В таком случае
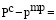
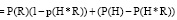. (12)
Значение первого члена в выражении (12) всегда будет положительным. Значение вероятности будет больше того, которое соответствует выбранным ранее значениям rg0 в случае, когда рассматриваются показатели Fi(i ∈ IR ∩ IH), при учете оптимальных значений hg0, и будут любые значения rg. Тогда мы сможем убедиться, что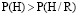 
. Будет положительной в таком случае оценка (12). Что может иллюстрировать получаемый результат? Большая эффективность в работе киберфизических систем получается вследствие применения современных подходов в управлении. На базе многоканального подхода необходимо формировать соответствующий модуль в ходе анализа ресурсного обеспечения киберфизической системы. В виде группировки могут быть представлены несколько типовых структур, когда он реализуется [9]. Они будут следующие: сходящиеся, расходящиеся и с учетом обратного. Для конвергентной структуры мы придем к следующему выражению при рассмотрении комбинации ресурсной и управленческой составляющих [10]:
Uconv = (r1inp,... rjinp,... r7inp,hcon).
Придем к такому выражению, когда структура будет расходящейся:
Udiv = (r,hdivr1inp,... rjinp,... r7inp).
Мы придем к такому выражению, если структура будет перевернута:
Urev = (r,hdiv , rRout, rRin).
Выбор относительно наилучшего сочетания Ucpnv, Udiv, и Urev необходимо сделать на основе показателей Fi (i = 1,I). Это будет соответствовать оптимизации рассматриваемой системы.
Оптимизация ресурсов киберфизической системы. То, как работает сходящаяся и расходящаяся структура, определяет, как работает модуль в многоканальном подходе. Расходящаяся структура будет иметь большее влияние. Что является причиной этого? Между конкретными видами деятельности информационной системы осуществляется процесс распределения программно-аппаратных ресурсов. Первичные источники в ресурсах связаны с особенностями конвергентной структуры. Виды деятельности в информационных системах разнообразны [11]. Количество ресурсов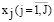 
должно быть рационально распределено. Для этого в структуре информационной системы необходимо определить степень приоритетности каждого из j-го вида деятельности. Анализ показывает, что перспективным является подход, основанный на экспертной оценке с использованием априорного ранжирования. Целесообразно перевести полученные абсолютные приоритеты 
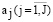в относительный вид
.
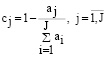Будет показывать целевая функция, насколько оптимальным будет распределение
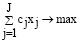. (13)
Также существуют ограничения:
а) по значениям мощности компонентов информационной системы в подразделениях организации
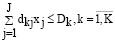. (14)
В указанном выражении dkj показывает значение средней загрузки информационной системы в k-м отделе; Dk – величина гарантированного временного объема работы в k-м отделе;
б) компонентами ресурсного обеспечения, которые носят многоканальный характер
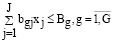. (15)
В этом выражении bgj рассматривается для j-го вида деятельности организации как значение коэффициента использования g-го ресурса; Bg рассматривается как величина суммы залога, которая ожидается по g-му ресурсу. При ресурсном обеспечении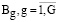 
, которое является многоканальным, а также при загрузке киберфизической системы 
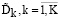в подразделениях поведение носит стохастический характер. В связи с этим для ограничений (14), (15) учитывается вероятностный характер:
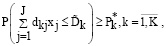
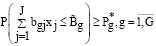. (16)
В указанном выражении при выполнении ограничения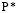 
задано значение вероятности. Можно использовать детерминированные ограничения (14), (15) вместо (16) при наличии закона распределения случайных величин. Также необходимо составить план распределения ресурсов между видами деятельности в киберфизической системе организации 
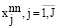. Есть альтернативные варианты для тех ресурсов, которые планируются:
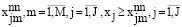. (17)
В этом выражении m рассматривается как количество таких альтернатив, которые будут возможны. Укажем альтернативную переменную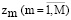 
, которая будет соответствовать m-му варианту в тех ресурсах, которые будут планироваться
.
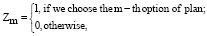
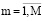Если учесть целевую функцию (13), а также ограничения (14), (15), (16), то оптимизационная модель при задании m-го варианта будет представлена следующим образом
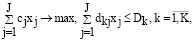
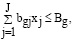
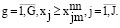(18)
Задача оптимизации (18) рассматривается с точки зрения подхода, использующего линейное программирование. Выполним процесс замены переменных
.
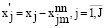Затем перейдем от обозначения (18) к такому представлению:
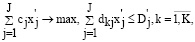
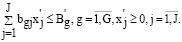(19)
В указанном выражении есть определенные ограничения:
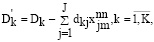
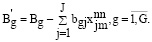(20)
В них замечено, что правые части будут зависеть от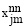 
. Мы можем переписать, используя альтернативную переменную 
:
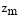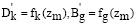. (21)
Будем считать, что в (20)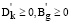 
. Затем мы рассмотрим двойственную задачу линейного программирования:
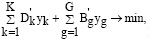
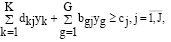
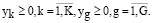(22)
В этой задаче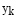 
показывает, насколько избыточна мощность информационной системы, 
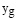показывает, насколько избыточно предоставление ресурсов. В этом случае требуется осуществить запланированный вариант 
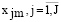. Можно говорить об избыточности соответствующего ресурса по сравнению с другими ресурсами, когда в двойственных переменных их оптимальное значение близко к нулю. В этой связи максимальное значение в целевой функции, относящейся к задаче (22) по набору переменных 
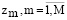, приводит к рациональному балансу возможностей информационной системы организации и ресурсов
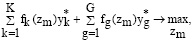
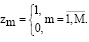(23)
Метод вариационного моделирования позволяет осуществить по распределению ресурсов рациональный выбор варианта на основе многоканального подхода на основе (23). В этом случае задача решается со значением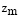 
для каждого из шагов, на которых осуществляется поиск в задачах (19), (22). Для осуществления процесса окончательного распределения ресурсов может использоваться экспертная информация, в которой учитывается мнение руководства организации.
Результаты исследования и их обсуждение
Были построены регрессионные модели для того, чтобы проводить математическое описания того, какими будут статистические зависимости по каждой из пар показателей. Описать существующие отношения можно на их основе. Было проведено построение моделей. В ходе рассмотрения они были разных типов: логистические, S-кривые, линейные, дважды обратные, экспоненциальные, обратные по X (Y), логарифмические по X, мультипликативные, квадратные по X (Y). В качестве оптимальной считалась такая модель, для которой получался максимальный коэффициент детерминации (R2), а также минимальная средняя ошибка. В таблице мы привели полученные модели.
Заключение
В работе рассмотрены возможности работы киберфизических систем, которые могут функционировать в различных организациях. Даны предложения по оптимизации многоканальной системы ресурсного обеспечения организации. Показано, каким образом могут распределяться ресурсы. Приведены результаты моделирования.
Регрессионные модели, позволяющие описать взаимосвязь показателей, характеризующих состояние киберфизической системы, с результатами деятельности организации
|
Независимые переменные (X) |
Зависимые переменные (Y) |
|
|
Число переданных сообщений |
Объемы информации, требующие повторной обработки |
|
|
Общая нагрузка оборудования |
Y = 1/(0,001153 + 0,000013*X) |
Y = 1/(0,0498 – 0,0035*X) |
|
Деятельность по обслуживанию оборудования |
Y = 259,851 + 46956,5/X |
Y = 1/(–0,0238 + 0,000484*X) |
|
Занятость рабочего места в течение года |
Y = 219,853 + 144657/X |
Y = 572,151 – 93,5932*lnX |
|
Независимые переменные (X) |
Зависимые переменные (Y) |
|
|
Объемы новой информации |
Потери информации |
|
|
Общая нагрузка оборудования |
Y = –0,6803 + 77,6279/X |
Y = 1/(0,2930 – 1,3119/X) |
|
Деятельность по обслуживанию оборудования |
Y = –11,7182 + 0,227449*X |
Y = –17,2573 + 2356,28/X |
|
Занятость рабочего места в течение года |
Y = 1/(–0,0095 + 33,6416/X) |
Y = –16,0162 + 6445,45/X) |
Библиографическая ссылка
Львович Я.Е., Аветисян Т.В., Преображенский А.П. МОДЕЛИРОВАНИЕ И ОПТИМИЗАЦИЯ РЕСУРСОВ В КИБЕРФИЗИЧЕСКИХ СИСТЕМАХ // Современные наукоемкие технологии. – 2022. – № 12-1. – С. 40-45;URL: https://top-technologies.ru/ru/article/view?id=39434 (дата обращения: 21.11.2024).