Основная часть теоретико-игровых моделей пространственной конкуренции используют двушаговую некооперативную игру. На первом шаге каждая фирма выбирает месторасположение, часто интерпретируемое как решение о распределении товаров. Затем, на втором шаге, фирмы соревнуются ценовыми политиками. Теоретически, все подобные двушаговые модели подразумевают лояльность покупателей, так как могут выбирать товар любой фирмы и подразумевается, что они готовы заплатить запрашиваемую стоимость. В данной работе используется стандартный подход использования двух шагов, на первом из которых фирмы одновременно выбирают место расположения, а на втором шаге алгоритм становления цен не определяется. Вместо этого ценовые политики моделируются через идею кооперативной игры. Такое использование этой идеи порождает модель ценовой политики, в которой покупатели наравне с фирмами принимают непосредственное участие в определении цен. Соответственно, это порождает метод анализа, который не обязательно подразумевает свободу фирм при выборе цен.
Существует несколько стимулов нахождения модели, в которой не обязательно подразумевается свобода фирм при выборе цен. Один из них заключается в определении достаточных условий, при которых фирмы будут выбирать социально эффективное месторасположение, т.е. месторасположение, при котором экономическая выгода от взаиморасчетов фирм и покупателей будет максимальной. Одно из достаточных условий для эффективности в играх месторасположения (пространственного конкурирования) было рассмотрено в работах [1, 2, 3]. Данная работа учитывает основной результат этих работ, но использует его для других целей. В то время как в работах [1, 2, 3] использовали модель для ограничения возможных стратегий ценообразования, данная работа использует модель для применения стратегий ценообразования. Основные результаты полагались как последовательности свободных сделок между покупателями и фирмами. При альтернативном использовании основы важна необходимость двух условий для эффективной пространственной конкуренции: фирмы выбирали месторасположение в соответствии с условием безвнешности и игры второго шага имеют структуру с раздельными значениями, в которых создаваемое значение можно представить через взаимоотношение покупателей. Выделяются два следствия основного результата, которые заключаются в объяснении наличия в моделях ценообразования пространственного конкурирования: в результате идеальное снижение цен порождает эффективное уравнение. В силу того что идеальное снижение цен в подобных моделях приближает каждую фирму к ее крайнему потреблению, каждая фирма действует так, как если бы она торговала на рынке с идеальными конкурентными условиями. В работе [4] в теоретико-игровой версии второй теоремы благосостояния показано, что идеальная конкуренция при условии безвнешности является достаточным условием для того, чтобы эффективное производство описывалось уравнением. Так как модели с ценовым понижением удовлетворяли условию безвнешности, их эффективные результаты относились к не полностью идеальным дополнениям ко второй теореме благосостояния. Второе следствие основного результата заключается в том, что результаты, полученные [1, 3], можно обобщать бесконечно. С использованием главного результата показано, что этих изменений можно избегать, гарантируя, чтобы стратегия оценки каждой фирмы отразила структуру ее крайнего вклада. В игре местоположения это подразумевает, что стратегия оценки фирмы должна быть определена покупателем. Заключительное следствие для непринятия ценового урегулирования заключается в том, что во многих деловых ситуациях цены определяются в результате некоторых типов взаимодействия свободной формы, например переговоров. Вопреки многим потребительским рынкам фирмы могут не иметь политики ценообразования. Для таких случаев вариант анализа, который не принимает априорную ценообразовывающую политику, будет информативен. Чтобы обеспечивать такой анализ, в данной работе на втором шаге моделируется кооперативная игра, а затем рассматривается основа [5–7]. Основа выбирается в начале, когда рыночные ситуации моделируются как кооперативные игры, для которых существует алгоритм решения, моделирующего конкуренцию, и основной результат может интерпретироваться как следствие взаимодействий всех игроков [7–10].
Рассмотрим пример, представленный на рисунке, с двумя фирмами и случайно разбросанными по горизонтальной прямой покупателями. Фирма 1 занимает место a1, а фирма 2 – место a2. Кривая с левой вершиной представляет собой функцию привлекательности товара фирмы 1 для покупателей, а кривая с правой вершиной представляет собой функцию привлекательности товара фирмы 2 для покупателей. Данные кривые также случайны.
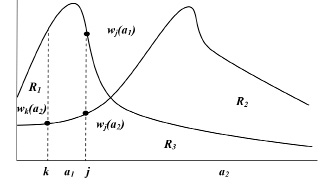
Графическое изображение постановки задачи
Будем считать, что покупатель j готов платить ωj(a1) за товар фирмы 1 и ωj(a2) за товар фирмы 2, цены приравняем к нулю. Предположим, что каждая фирма может поставить любое количество товара. Применительно к основному исходу ни одно подмножество игроков не может увеличить свой выигрыш, действуя обособленно. Данное свойство используется, чтобы показать, почему основа может быть представлена в виде алгоритма конкурентного решения.
Рассмотрим покупателя j на рисунке. Привлекательность товара фирмы 1 для него больше, чем привлекательность товара фирмы 2 (ωj(a1) > ωj(a2), поэтому он будет покупать товар фирмы 1. Более того, он не заплатит больше ωj(a1) – ωj(a2) за товар. Таким образом, появляется анализ основы. Так как фирма 2 может обеспечивать весь рынок, он будет иметь избыточную мощность. Теперь предположим, что покупатель j заплатил фирме 1 цену pj > ωj(a1) – ωj(a2). Тогда покупатель j получает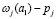 
экономической выгоды, которая меньше, чем ωj(a2). Но это свидетельствует, что покупатель j и фирма 2 могут увеличивать взаимную выгоду, торгуя друг с другом по любой цене 
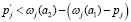. Покупатель с большей вероятностью откажется, так как он может получить 
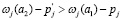. Так же, так как 
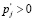, фирма 2 откажется, так как в противном случае она не продаст товар вообще. Таким образом, в основе, 
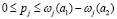. Заметим, что выражение ωj(a1) – ωj(a2) показывает всего лишь преимущество расположения фирмы 1 к покупателю j. Если такое же преимущество фирма имеет ко всем покупателям, предпочитающим ее товар, то будем иметь подавляющее превосходство фирмы 1 по расположению, обозначенное как R1 на рисунке 1. Так как 
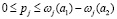для всех покупателей j, предпочитающих товар фирмы 1, следовательно, доход фирмы 1 в любой точке может варьироваться от 0 до R1.
Рассматривая область R1, видим, что преимущество месторасположения фирмы есть не что иное, как ее крайние издержки. Если фирма 1 не участвует в игре, покупатели будут приобретать товар фирмы 2. Это приведет к появлению экономического дохода R2+R3. Так как при участии фирмы 1 экономический доход составит R1+R2+R3, крайние издержки фирмы 1 R1.
Следует отметить, что основа игр расположения обычно не определяет единственный выигрыш. Как правило, она определяет, что фирма получит что-то от нуля до своей предельной доли, и покупатели обычно гарантированно получают какую-то выгоду, изображенную как R3.
Рассмотрим покупателя k на рисунке. Положим, аналогично покупателю j он выбирает товар фирмы 1. Также аналогично товар для него предпочтителен в той же степени. Однако он находится в другом конкурентном положении. В отличие от покупателя j он имеет худшую альтернативу, т.е.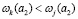 
. Таким образом, в структуре ценообразования соответствующей конкурентной модели можно ожидать, что покупатели j и k заплатят разные цены. Данный пример используется для демонстрации условий безвнешности и различности значений. Так как значение складывается из R1+R2+R3, необходимо заметить, что эта область равна сумме значений выигрышей покупателей от каждой сделки и затем сложенной по каждому покупателю. Для условия безвнешности уточним, что без фирмы 1 значение в игре станет R2+R3. Более того, где бы ни располагалась фирма 1, значение R2+R3 останется неизменным. Условие безвнешности состоит в том, что не существует внешних условий при данном стратегическом выборе игрока (выборе месторасположения фирмы 1), который изменят значение, которое можно получить (R2+R3) без данного игрока. Предопределяя важность данного условия, заметим, что при фиксированном R2+R3 фирма 1, максимизируя R1, так называемое общее создаваемое значение. Таким образом, решение фирмы о максимизации своей прибыли увеличивает общую выгоду. Второй шаг модели в этой работе есть кооперативная игра трансферабельной полезности (TU), а именно игра, в которой имеются набор игроков N и характеристическая функция 
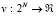. Для любого 
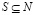параметр v(s) обозначается максимальную экономическую полезность, которую игроки из S могут для себя вынести. Результат TU кооперативной игры описывается распределением 
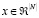, где компонент xi обозначает полезность, получаемую игроком i. Основа TU кооперативной игры есть набор распределений (N;v), удовлетворяющих условию 
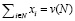, и для всех 
.
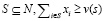Определим TU кооперативную игру (N;v) как игру с обособленными покупателями, если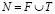 
, где 
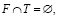
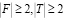, и если характеристическая функция удовлетворяет следующим условиям: для любых 
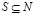таких, что 
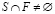и 
,
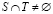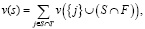(1)
и ес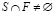ли 
или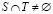 
, то v(s) = 0. Допуская, что F – набор фирм, а Т – набор покупателей, игра с обособленными покупателями станет игрой совпадений, в которой экономическая ценность коалиции может быть представлена в покупательском базисе. Для того чтобы получить такую раздельную форму, в пространственных моделях часто делают два предположения: каждая фирма может снабжать всех покупателей и крайние издержки производства являются постоянными. Чтобы продемонстрировать, как эти два предположения согласуются с условием (1), для начала рассмотрим пример, в котором фирма i имеет только одну единицу товара на продажу, но при этом двух покупателей j1 и j2, желающих купить этот товар. Тогда значение коалиции {i,j1,j2} выражается в прибыли от продажи товара наиболее заинтересованному покупателю. Используя характеристическую функцию, представим это в следующем виде 
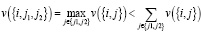. Как прежде, обозначим покупателей j1 и j2, каждый из которых претендует на одну единицу товара фирмы i. Предположим, что фирма i имеет достаточно товаров для всех покупателей, но ее крайние издержки производства уменьшаются. Тогда в характеристической функции 
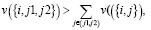снова условие принуждения (1). Следует аналогичный пример, но с увеличивающимися издержками производства 
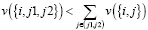. Игра с обособленными покупателями имеет свойство непустой основы, и диапазон выигрышей фирм легко охарактеризовывается. Игра с обособленными покупателями имеет непустую основу. В ее основе каждый игрок 
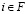получает между 0 и его крайним вкладом:
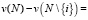
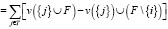[11-15].
На первой стадии модели фирмы выбирают месторасположение. Пусть для каждого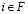 
, Ai суть конечный набор, представляющий возможные выборы месторасположения для фирмы i. (Конечность – единственное ограничение на Ai.) Далее определяем набор A как 
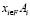с типичным элементом a. Чтобы в качестве последствий выбора месторасположения фирмами иметь игры с обособленными покупателями, сначала рассмотрим произвольную функцию 
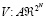. Обратим внимание, что для любого профиля 
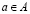, V(A) – характеристическая функция, а именно функция от 
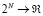. Главная модель этой работы тогда представляет собой набор 
с условием, что для каждого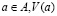 
– игра с обособленными покупателями. В наборе игр с обособленными покупателями последствие от выбора фирм будет в общем случае диапазоном результатов, нежели уникальным результатом. Конкуренция цен, как представлено в основе, подразумевает, что фирма может получить не больше своей доли на рынке, но не меньше 0. Следовательно, чтобы фирмы могли оценивать различные месторасположения, необходимо расставить приоритеты на интервале [0,b], где b – неотрицательное число. Так как интервалы имеют тот же самый минимум, то предпочтение фирмы по таким интервалам может быть охарактеризовано с условием нестрогого доминирования: для любого b ≥ 0 и c ≥ 0, 
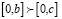если b>c, и, 
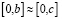если b=c. В наборе игр с обособленными покупателями, если основа используется для моделирования конкуренции, условие (WD) будет подразумевать желание игроков максимизировать свои доли [16, 17]. Рассмотрим набор 
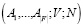игр с обособленными покупателями. Для каждого 
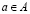через πi(a) обозначим оценку i-ой фирмой множества своих основных исходов. Если предпочтения фирмы i удовлетворяют условию (WD), то для любого 
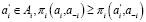тогда и только тогда, когда
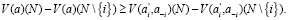
Набор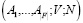 
игр с обособленными покупателями удовлетворяет безвнешности (NE), если для любого 
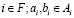и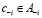 
,
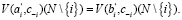
Рассмотрим набор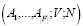 
игр с обособленными покупателями, который удовлетворяет условию безвнешности (NE). Если предпочтения каждого игрока удовлетворяют условию (WD), тогда для любого 
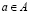, которое максимизирует 
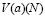представляет собой уравнение [18, 19].
Заключение
Итог работы в том, что, если нет условия безвнешности и условий раздельных значений, любое эффективное распределение месторасположений представляет собой уравнение. Если выбор месторасположений игроками удовлетворяет условию безвнешности, тогда профиль эффективных решений представляет собой уравнение, пока игроки стремятся максимизировать свои доли на рынке. В данной работе причины того, почему фирмы стремятся максимизировать свои доли, можно обобщить двумя шагами: анализом основы игры с обособленными покупателями показываем, что издержки производства варьируются от 0 до всей доли фирмы, и, получив набор решений, с необходимостью удовлетворяющих нестрогому доминированию, фирмы выберут месторасположение, гарантирующее максимальную долю на рынке.
Библиографическая ссылка
Зайцева И.В., Шлаев Д.В., Теммоева С.А., Филимонов А.А., Демчук А.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КООПЕРАТИВНОЙ ИГРЫ ДЛЯ АНАЛИЗА ЦЕНОВОЙ ПОЛИТИКИ ФИРМЫ // Современные наукоемкие технологии. – 2022. – № 12-1. – С. 35-39;URL: https://top-technologies.ru/ru/article/view?id=39433 (дата обращения: 21.11.2024).