Важное значение в обучении математике на всех уровнях образования имеет понимание онтологической детерминированности структур различных систем чисел и фигур, а также знание их генезиса и принципов построения более сложных структур. Определенность таких структур достигается выявлением минимальных структур и их инвариантов, обладающих категориальными (наиболее общими) системными признаками. Отсюда и следует основная концепция методологии интегральной математики: научиться определять базовые минимальные структуры системы и изменять их в соответствии с поставленной целью и с сохранением категориальных признаков.
Цель исследования: на основе методологических принципов комплексного подхода [1] определить методическую линию в обучении математике бакалавров педагогического вуза, ориентированную на формирование универсальных и общекультурных компетенций у студентов. Для этого в структурах или системах методических объектов выделяются категориальные признаки, для которых характерна онтологическая двойственность двух субстанциональных начал в виде единства противоположностей: количество – качество, содержание – форма, целое – часть, индукция – дедукция, теоретическое – практическое и т.д. В математическом образовании двойственность проявляется как: положительное – отрицательное, дифференцирование – интегрирование, арифметическое – геометрическое (число – фигура), линейное – нелинейное, непрерывное – дискретное и т.д. При этом переход от одной формы представления объекта (понятия) к другой форме всегда осуществляется в присутствии третьего начала – отображения или преобразования. Возникающую при этом проблему улучшения качества математической подготовки бакалавров педагогического образования предлагается разрешить на основе кумуляции идей и интеграции структур различных предметных областей, выделением категориальных признаков методических объектов образовательной деятельности.
Материалы и методы исследования
Здесь мы будем исследовать образы методических объектов относительно некоторых отображений с позиций методов интегральной математики. Одним из основных подходов исследования объектов и структур в интегральной математике будем считать комплексный подход, тесно связанный с системным подходом. Понятие «системное» воспринимается как «целостное», а «комплексное» – как «связное в системе», т.е. как «часть целого». Под интегральной математикой мы будем понимать систему знаний, понятий и методов собственно математики, математических дисциплин, реализующих междисциплинарные (эконометрика, биометрика, фрактальная геометрия и т.д.) и трансдисциплинарные (математическая эвентология, сакральная геометрия, синергетика, семиотика и т.д.) взаимодействия в виде схем, структур и их математических моделей [2]. Построение сложных алгебраических, геометрических и порядковых структур происходит по одним и тем же логическим, аксиоматическим и комбинаторным схемам. При этом отождествление алгебраического начала (числа) и геометрического начала (точки) происходит в соответствии с законом единства противоположностей как единства формы определенности качества и количественной определенности содержания. По аналогии с математическими объектами наблюдается также единство компонентов в различных структурных образованиях с точки зрения компетентностного подхода к образовательной деятельности.
Результаты исследования и их обсуждение
Проанализируем эту ситуацию по отношению к образовательной деятельности, и в частности к математическому образованию в педагогическом вузе. В образовательной среде различными исследователями выделяются пространственно-предметный, социальный и психодидактический компоненты (В.И. Панова), а в школьной образовательной среде выделяются такие структурные единицы, как физическое окружение, человеческий фактор и программа обучения (Г.А. Ковалева) [3]. C другой стороны, по мнению Ю.Г. Кублицкой, познавательная компетентность в образовательной деятельности, как психолого-педагогическая категория, содержит мотивационно-ценностный, когнитивный, операционно-деятельностный и рефлексивно-оценочный компоненты [4]. Хотя, по нашему мнению, специально выделить когнитивный компонент не было никакой необходимости, поскольку «когнитивный» в переводе на русский язык и означает «познавательный». Следует отметить, что в образовательной деятельности в качестве ключевых компонентов выступают: рефлексивно-оценочный компонент, направленный, в первую очередь, на активизацию самостоятельной работы студентов, необходимой в дальнейшей профессиональной деятельности, и познавательный компонент, отвечающий за овладение предметными знаниями. Соотношение объемов контентов этих компонентов в ту или иную сторону определяет эффективность образовательного процесса в целом, и математического образования в педагогическом вузе в частности.
Анализ подготовки учителей математики в условиях новых государственных стандартов по направлению «Педагогическое образование», проведенный Далингером В.А., показывает, что указанное выше соотношение знаниевых контентов (познавательной активности) студентов не в пользу предметной составляющей. Поэтому автор делает вывод о необходимости актуализации компетенций, непосредственно связанных с активизацией математической подготовки в направлении усиления школьного компонента математического образования и комплексного изучения фундаментальных математических курсов, адаптируя их содержание и структуру к современным требованиям развития науки, образования и общества [5].
Кроме того, в этом направлении особый упор следует делать на формирование специальных профессиональных компетенций, ориентированных на развитие критического и комплексного мышления студентов, использование полученных математических знаний для решения профессиональных задач, а также понимание универсального характера математических законов применительно к различным сферам человеческой деятельности [6]. В более общем контексте, в философских обобщениях педагогических категорий, например, бытие в целом определяется такими сферами (компонентами), как биотехносфера (материальный мир), психосфера, культуросфера, социосфера [7].
Таким образом, проведенный нами анализ структуры образовательной деятельности и образовательной среды показывает внутреннее (сущностное) сходство категориальных признаков (изоморфизм) и составляющих базовых компонентов. Так, например, пространственно-предметному компоненту по В.И. Пановой соответствует компонент программного обучения по Г.А. Ковалевой, или когнитивный компонент по Ю.Г. Кублицкой, предметная составляющая по В.А. Далингеру и компонент биотехносферы по Н.С. Розову. Хотя эти компоненты по-разному и называются, но их категориальная основа одна и та же – материальный атрибут знаниевого контента.
Выявляя внутреннее сходство компонентов (изоморфизм) педагогического образования и образовательной среды, а также обнаруживая соответствие базовых понятий математики, естественных наук и социосферы, методологию интегральной математики (и математического образования в целом) мы строим, исходя из единства следующих составляющих образовательной деятельности: субъекта, общества (социума), мира (природы), знания (веры, религии, духовного мира). Такой подход к математическому образованию мы называем комплексным, или системно-деятельностным подходом. Считаем, что такое образование должно подчиняться правилу 4Ц: образование (знание) должно быть цельным, ценным, целостным и целесообразным.
В методологии интегральной математики мы выделяем два аспекта: системный и познавательный. Иерархию в системе методических объектов в методологии интегральной математики определяем следующим образом. Считаем, что базовым множеством элементов является множество, состоящее из точек, чисел и отображений. Далее системный блок строится выбором методологических принципов, на основе которых строятся базовые математические структуры по определенным схемам, допускающие обобщения по определенному категориальному плану. В познавательном аспекте допускается возможность введения в базовом множестве различных операций и отношений, с помощью которых строятся более сложные фигуры и выражения, среди которых выделяются так называемые структурные единицы. Обычно в определении структурной единицы в некотором множестве допускается выбор минимально возможного числа операций (отношений) и минимум требований к ним. Помимо операций и отношений, мы также вводим такие действия, как итерация, суперпозиция и дополнение. Эти действия выполняют вспомогательную роль в построении познавательной стратегии процесса обучения предмету. Таким образом, системный и познавательный аспекты в единстве позволяют конструировать более сложные структуры, исследовать их на основе фундаментальных методологических законов математики. Отбор содержания математического образования происходит в соответствии с требованиями федеральных государственных образовательных стандартов и программных документов с поставленной целью достижения познавательного и учебного результата. Таким образом, структурные компоненты методологии интегральной математики взаимосвязаны как по вертикали, так и по горизонтали: по вертикали происходит развитие понятия или структуры от простого к сложному, а по горизонтали определяют стратегию построения новых понятий (схема «Структурные компоненты»).
С другой стороны, в методологии интегральной математики, и в математическом образовании в целом, мы выделяем системно-деятельностный, познавательный, ценностно-смысловой (воспитательный, креативный) аспекты. Познавательный аспект деятельности позволяет изучить онтологическую связь базисных структур и методологию эволюции различных предметных областей. Так, например, просматривается аналогия закономерностей связей между базисными понятиями в конструировании методических объектов математических, естественно-научных и социально-гуманитарных дисциплин. Эти аналогии обнаруживаются на моделях базовых структур математики, природы и общества. При этом соответствие базовых структурных единиц различных моделей представления объектов осуществляется по определенной логической схеме. Например, модели «единица – единичный элемент – структурная единица» в математике соответствует модель «человек – семья – социальная группа» в обществе.
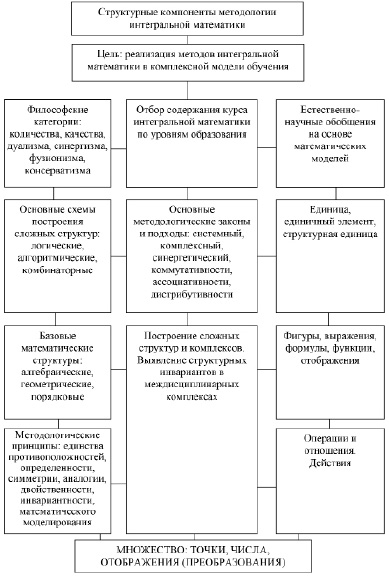
Рис. 1. Структурные компоненты
Единство структурных компонентов в методологии интегральной математики изобразим следующей схемой, называемой «Структурные компоненты» (рис. 1).
Взаимодействие базисных структур в компонентах такой образовательной деятельности происходит по схеме «Взаимодействие базисных структур» (рис. 2).
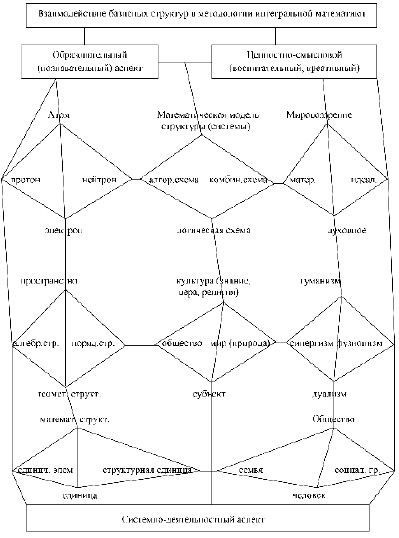
Рис. 2. Взаимодействие базисных структур
По схемам конструирования математических структур с помощью базовых понятий и структурных единиц, по законам коммутативности, ассоциативности и дистрибутивности введенных операций, происходит образование, например, молекул сложных химических (физических) веществ (материи) посредством ковалентной, ионной и водородной связей, которым свойственны такие же инвариантные действия, что и аналогичным структурам математики. Так, например, для валентностей или степеней окисления в сложных химических соединениях выполняются аналоги законов коммутативности или ассоциативности. Действительно, если Х и У – химические элементы валентностей α и β, и m, n – число атомов этих элементов соответственно, то в сложном соединении ХУ выполняется равенство α m = β n. Это один из важнейших законов химии, называемый законом постоянства состава вещества и имеющий важное значение при составлении химических уравнений и определении типов химических реакций. Или же в социологии для двух субъектов х и у общества отношение толерантности * должно подчиняться закону коммутативности, т.е. х*у = у*х.
Заключение
Таким образом, сходство категориальных признаков методических объектов в структурных компонентах методологии интегральной математики позволяет установить внутреннюю связь базовых компонентов различных сфер деятельности и предметных областей, на основе которых строятся сложные комплексы по аналогии с соответствующими компонентами математического образования. Такое сходство действий способствует развитию целостного восприятия методического объекта, обнаруживая при этом определенные структурные инварианты междисциплинарного характера, представляемые как базовые минимальные структуры, обладающие категориальными признаками. Выявление таких признаков методических объектов различных предметных областей и построение более сложных структур (комплексов) происходит по одним и тем же логическим схемам, свойственным математическим структурам. Такой подход к математическому образованию в педагогическом вузе способствует качественному отбору содержания математических дисциплин в соответствии с требованиями ФГОС ВО.
Библиографическая ссылка
Ярахмедов Г.А. О КАТЕГОРИАЛЬНЫХ ПРИЗНАКАХ МЕТОДИЧЕСКИХ ОБЪЕКТОВ В МЕТОДОЛОГИИ ИНТЕГРАЛЬНОЙ МАТЕМАТИКИ // Современные наукоемкие технологии. 2022. № 11. С. 239-244;URL: https://top-technologies.ru/ru/article/view?id=39428 (дата обращения: 07.02.2026).
DOI: https://doi.org/10.17513/snt.39428



