Важным импульсом в развитии любого общества являются постоянно развивающиеся научные области. Школе же отводится главная роль в формировании компетенций учащихся, которые будут готовы воспринимать и транслировать полученные знания, применять их в профессиональной и практической деятельности. Поэтому важно подготовить квалифицированного педагога, который поможет в достижении обозначенных целей [1]. Профессиональное мышление, педагогические компетенции педагога формируются еще в стенах вуза [2]. Наряду с изучаемыми фактами из различных областей будущие педагоги должны овладеть системой общеучебных, предметных, методических и в целом профессиональных действий [3, 4]. Такие знания, способы действий и умения их применять в различных ситуациях составляют содержание практико-ориентированных методических компетенций педагогов. Поэтому проблема поиска способов, технологий их формирования у будущих педагогов актуальна.
Каждая изучаемая в педвузе дисциплина должна вносить определенный вклад в общее становление педагога. Освоение практико-ориентированных компетенций должно быть встроено в учебный процесс вуза [5]. Так, большой удельный вес в становлении методических компетенций студентов-математиков педвуза имеет дисциплина «Методика обучения математике» [2]. В ее содержании отражено множество методических концепций – от обучения математическим понятиям, теоремам, решению задач до методики обучения конкретным темам школьного курса математики.
В данной статье мы подробно охарактеризуем технологию формирования действий будущих педагогов по построению средств формирования математических понятий у школьников как основы их методической подготовки.
Цель исследования – выделить приемы конструирования упражнений для обучения учащихся математическим понятиям и разработать методические рекомендации по их использованию в процессе методической подготовки студентов педвузов.
Материалы и методы исследования
Образовательной средой, в которой проводились наблюдения, разрабатывались и апробировались обучающие средства, была выбрана среда физико-математического факультета ФГБОУ ВО «Мордовский государственный педагогический университет имени М.Е. Евсевьева». Применялись общепринятые методы исследования – анализ научной, методической, учебной литературы, анкетирование и обработка результатов исследования.
Содержание статьи обладает практической значимостью не только для студентов педвузов, но и для учителей, преподавателей методических дисциплин.
Результаты исследования и их обсуждение
Формируемые у студентов компетенции представляют собой методические знания, умения, способы действий и опыт их применения на практике. Такие компетенции базируются, прежде всего, на школьных знаниях: определений математических понятий, содержательных взаимосвязей между ними, их классификациях. Также основополагающими являются знания основ геометрии, теоретических основ курса алгебры, элементарной математики, математической логики, дидактики, психологии. Важным является понимание деятельностной основы построения многих методических концепций. Студенты должны иметь представления о том, что изучаемое содержание не сводится только лишь к заучиванию фактов и положений, а предполагает формирование адекватной ему системы действий. В частности, у студентов необходимо сформировать систему методических действий по обучению учащихся математическим понятиям.
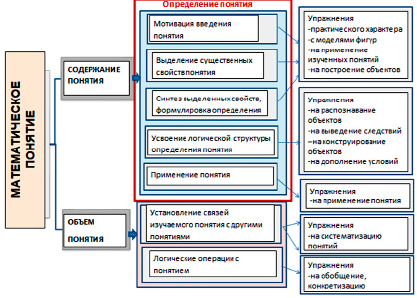
Рис. 1. Схема формирования математических понятий

Рис. 2. Общий прием конструирования упражнений для обучения математическим понятиям
Формирование математических понятий – сложный мыслительный процесс, включающий каскад логических приемов. Обучение понятиям имеет математическую, логическую, методическую основу, начиная с определения понятий и заканчивая их включением в систему имеющихся у человека знаний. Подробно методическая концепция формирования математических понятий описана в трудах Г.И. Саранцева [2].
На рис. 1 приведена общая схема, в которой поэтапно раскрыт процесс образования математических понятий. Также в ней указаны основные типы упражнений, выполняющие определенные функции на каждом из этапов работы с понятием.
Как видно из схемы, первоначальным звеном в изучении понятия является выделение его существенных свойств, которые затем войдут в определение. Не менее значимым является этап усвоения логической структуры определения, на котором ведется работа с необходимыми и достаточными условиями существования определяемого объекта. Затем переходят к изучению других свойств понятия, его признаков, эквивалентных определений и применяют понятие в различных ситуациях. Заключительным моментом является систематизация изученного, определение места данного понятия в системе других понятий.
Как же реализовать в практике обучения математике такой сложный процесс, как формирование понятия? Как включить учеников в продуктивную познавательную деятельность? Все эти вопросы встают перед студентами педвузов. Причем первые трудности появляются у них, когда необходимо подобрать или составить задания для выделения существенных свойств понятия, усвоения логической структуры определения, для систематизации понятий. Неудивительно, ведь таких упражнений очень мало в учебниках математики.
Для преодоления перечисленных трудностей нами была выделена последовательность действий по конструированию таких упражнений. Общий прием конструирования упражнений для обучения математическим понятиям приведен нами в статье [6]. Напомним его (рис. 2).
Из перечня обобщенных действий этого приема видно, что в приобретении студентами методических умений важным является умение выяснять виды определений понятий, проводить их анализ. Так, большинство определений понятий, как и в любой науке, в математике образованы через указание рода и видовых отличий. С учетом этого приведем характеристику частных приемов конструирования упражнений для реализации тех этапов формирования понятий, которые, как мы указали выше, вызывают наибольшие затруднения у студентов.
Прием конструирования упражнений (этап выделения существенных свойств понятия):
1. Опираясь на проведенный логико-математический анализ, указываем свойства объекта и связь между ними.
2. Если объект, принадлежащий понятию, можно без труда построить по указанным в определении свойствам, то можно составить упражнение на построение (в геометрии) или запись (в алгебре). Схема такого упражнения: «Постройте (запишите) объект, обладающий свойствами» (указываем свойства из пункта 1).
3. Если объем родового (видового) понятия составляют несколько видов, то можно предложить упражнение на группировку объектов по определенным свойствам.
4. Если изучаемый объект легко смоделировать на окружающих предметах или получить из моделей других объектов, то можно использовать упражнение с моделями фигур (на сгибание, разрезание).
5. В любом случае можно предложить решить задачу, в решении которой фигурируют свойства изучаемого объекта (геометрическую, алгебраическую, текстовую, практического характера).
Так, в определении смежных углов выделяют свойства: быть парой углов, иметь общую сторону, иметь стороны, продолжающие друг друга. Связаны эти свойства конъюнктивно. Построить объект с данными свойствами несложно (причем можно это сделать несколькими способами). Предлагаем, например, такое упражнение «Нарисуйте углы: прямой, острый и тупой. Продолжите одну из сторон этих углов». Далее характеризуем получившиеся углы и вводим термин «смежные углы».
Для первоначальной работы с понятием параллелограмма можно предложить упражнение «Разбейте предложенные четырехугольники на группы в зависимости от параллельности их сторон». При изучении арифметической прогрессии можно предложить задачу практического содержания о последовательности високосных лет.
Отметим и важность в изучении понятий использования наглядных операций на моделях фигур. Например, задание «Разрежьте бумажную модель равнобедренного треугольника так, чтобы линия разреза была параллельна одной из его сторон. Какие получаются фигуры?» Внимание учащихся обращается на полученную трапецию, у которой будут равные боковые стороны. Затем учащиеся дают определение равнобедренной трапеции.
Далее охарактеризуем последовательность действий для составления заданий для работы учащихся, как с необходимыми, так и с достаточными условиями существования объекта, подводимого под понятие.
Прием конструирования упражнений (этап усвоения логической структуры определения понятия):
1. Используйте таблицу для подведения объекта под понятие и составьте упражнение на распознавание объекта по схеме: «Укажите, какие из приведенных объектов принадлежат определению понятия».
2. Составьте упражнение на выведение следствий принадлежности объекта определению понятия по схеме: «Известно, что объект принадлежит понятию. Что отсюда следует?»
3. Составьте упражнение на конструирование объекта, принадлежащего понятию: «Постройте (запишите) объект, принадлежащий понятию».
Например, при работе с определением параллелограмма упражнением на распознавание будет такое: «Укажите, какие из четырехугольников, представленных на рисунке, являются параллелограммами». Здесь важно предложить четырехугольники, у которых нет ни одной пары противоположных сторон, имеется одна такая пара, и, наконец, среди них должны быть ромбы, прямоугольники, квадраты.
Упражнение «Четырехугольник ABCD – параллелограмм. Что отсюда следует?» способствует формированию у учащихся умения выводить следствия. Здесь важно понимать, что ответом на этот вопрос будут только те свойства параллелограмма, которые указаны в его определении.
Так, в алгебре при изучении квадратных уравнений выполнение следующего упражнения формирует у учащихся умение конструировать изучаемый объект: «Приведите примеры квадратных уравнений, старший коэффициент которых отрицательное число, второй коэффициент – число дробное, а свободный член – натуральное число».
Этап применения понятий предполагает решения задач на применение свойств и признаков понятия. Как подбирать и составлять блоки таких задач, какие еще средства можно использовать в этом случае, подробно описано в статьях [7, 8].
Хорошим подспорьем в плане систематизации изученных понятий будет использование упражнений для их классификации, выяснения объемов и отношений между ними. Особенно это важно, когда можно проводить классификацию объема понятия по нескольким основаниям. Приведем последовательность рекомендуемых в этом случае действий студентов, педагогов.
Прием конструирования упражнений (этап установления связей изучаемого понятия с другими понятиями):
1. Выясните объем изучаемого понятия, проведите его классификации по возможным основаниям (выделите классы объектов).
2. Составьте упражнения по следующей схеме:
«Верно ли, что: а) все <объекты 1> являются <объектами 2>; б) некоторые <объекты 1> являются <объектами 2>; в) все <объекты 1> являются <объектами 2>».
3. Составьте упражнение по схеме: «Изобразите связь между понятиями в виде кругов Эйлера – Венна».
Например, выясняя объем понятия параллелограмма, можно предложить упражнение «Выберите верные суждения: “Все квадраты являются прямоугольниками”, “Некоторые квадраты являются прямоугольниками”, “Некоторые ромбы являются квадратами”, “Все прямоугольники являются параллелограммами”, “Все ромбы являются параллелограммами”».
Использование таких приемов на занятиях по методике обучения математике позволило большей части студентов более технологично конструировать не только задания, но и проектировать уроки математики. Составляя на основе указанных приемов задания, студенты отбирали формы и методы работы с ними, применяли ту или иную технологию обучения для эффективного достижения целей урока.
Действительно, соответствие этапов урока и этапов формирования понятия нетрудно установить. В таблице оно приведено для урока, на котором учащиеся приступают к изучению нового понятия.
Соответствие этапов урока и этапов формирования понятия
|
Этапы урока |
Этапы формирования понятия |
|
Актуализация опорных знаний, способов действий |
Выделение существенных свойств понятия (решение задач с опорой на ранее изученные знания и способы действий) |
|
Постановка учебных задач |
Мотивация введения понятия |
|
Решение учебных задач |
Усвоение логической структуры определения понятия. Применения понятия в простейших ситуациях |
|
Рефлексия |
Оценивание деятельности по решению учебных задач |
Заключение
Технологии использования общего и трех частных приемов конструировании упражнений для обучения учащихся математическим понятиям могут быть перенесены в новые условия, как при изучении теорем, так и при обучении методам решения задач, обучении эвристикам. Упражнения можно дополнять, изменять, комбинировать. Их использование позволит включить учащихся в самостоятельную поисковую, эвристическую деятельность, организовать мини-исследования.
Выделенные в статье приемы способствуют формированию у студентов умений анализировать содержание школьных учебников математики, выявлять логическую структуру определений понятий, отбирать и проектировать дидактические средства для достижения целей уроков, выбирать наиболее целесообразные технологии обучения. Отраженное в статье содержание будет полезно учителям, а также аспирантам, магистрантам и преподавателям вузов.
Исследование проведено согласно техническому заданию гранта на проведение научно-исследовательских работ по приоритетным направлениям научной деятельности вузов – партнеров по сетевому взаимодействию (Чувашский государственный педагогический университет им. И.Я. Яковлева и Мордовский государственный педагогический университет имени М.Е. Евсевьева) по теме «Теория и технология формирования методических компетенций студентов-математиков педвуза».
Библиографическая ссылка
Сарванова Ж.А., Ульянова И.В. ТЕХНОЛОГИЯ ОБУЧЕНИЯ МАТЕМАТИЧЕСКИМ ПОНЯТИЯМ КАК СРЕДСТВО ФОРМИРОВАНИЯ МЕТОДИЧЕСКИХ КОМПЕТЕНЦИЙ СТУДЕНТОВ ПЕДВУЗОВ // Современные наукоемкие технологии. 2022. № 11. С. 198-202;URL: https://top-technologies.ru/ru/article/view?id=39421 (дата обращения: 01.01.2026).
DOI: https://doi.org/10.17513/snt.39421



