Рассматривается кусочно-интерполяционное приближение функций одной вещественной переменной с помощью интерполяционных полиномов Лагранжа и Ньютона с алгебраическим преобразованием на основе восстановления коэффициентов полинома по его корням. Преобразование имеет структуру алгоритма, который отличается [1] от формул Виета и уравнений Ньютона для симметрических функций [2]. Указаны конструктивные схемы вычисления коэффициентов и методика их выбора в соответствии точности приближения функции. Коэффициенты записываются массивом в раздел констант программы или хранятся как типизированный файл. Номер подынтервала, которому соответствуют коэффициенты, совпадает с номером строки массива или типизированного файла. С точностью до времени обращения к памяти время вычисления функции в этом случае пропорционально степени интерполирующего полинома. Ставится вопрос о связи временной сложности алгоритма вычисления функции с погрешностью приближения. Исследование выполняется с помощью численного и программного эксперимента. Достигается время вычисления O(1) при точности приближения порядка 10–19. Узловые значения на входе метода могут задаваться как значения решений обыкновенных дифференциальных уравнений. Этот аспект учитывается для разработки библиотеки стандартных программ вычисления функций, ее допустимых расширений и областей применения. С целью верификации достоверности приведены коды программ и результаты численных экспериментов.
Цель исследования: требуется показать эффективность программных реализаций предложенного метода. Акцент исследования делается на реальном достижении максимальной точности приближения функций при одновременной минимизации временной сложности. Цель включает обоснование широкой области и простоты применения библиотеки стандартных программ на основе предложенной реализации кусочной интерполяции.
Полином Лагранжа с равноотстоящими узлами интерполяции. Для интерполяции функции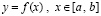 
, полином Лагранжа можно записать в виде
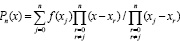, (1)
где xr – узлы интерполяции. Пусть на [a, b] взяты равноотстоящие узлы для полинома (1):
, 
,
, 
.
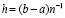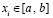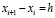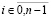Тогда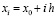 
, x0 = a, xn = b.
Отсюда
,
.
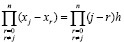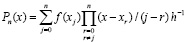С использованием переменной t = (x – x0)h–1 получится
, …, 
, 
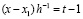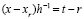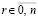, и
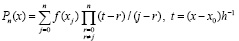. (2)
Прототип (2) изложен в [3]. Отличие составит перевод числителей из (2) в форму полиномов с числовыми коэффициентами. Пусть числитель дроби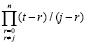 
записан в виде
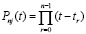, (3)
где роль корней полинома играют последовательные натуральные числа, среди которых пропускается j: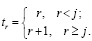 
В полиноме (3) восстанавливаются коэффициенты. Схема восстановления заимствуется из [1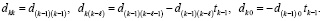; 4]:
(4)
Здесь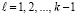 
. При k = n левые части (4) совпадут с искомыми значениями коэффициентов полинома (3). Получится:
.
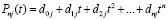Знаменатель в (2) отличается от числителя тем, что в нем t = j. В результате
, 
.
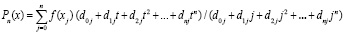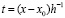Если собрать коэффициенты при равных степенях слагаемых, то
, 
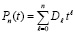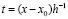, (5)
где Dl – результат приведения подобных.
Кусочная интерполяция. Ниже (2) – (5) реализуется на малых подынтервалах равной длины с общими границами разбиения
, 
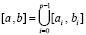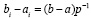. (6)
В частности, при p = 2k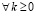 
справедлива оценка [5]:
, 
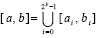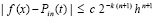
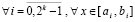, (7)
где Pin(t) – полином Лагранжа вида (5), построенный на подынтервале [ai , bi],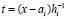 
, 
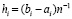– шаг интерполяции на [ai, bi], 
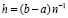. Оценка (7) показывает, что точность приближения растет с убыванием длины подынтервала и с ростом степени полинома. Полином (5) примет вид
, 
, 
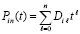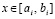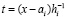, (8)
где коэффициенты Dil,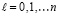 
, – результат приведения подобных на каждом подынтервале. Эти коэффициенты можно хранить в постоянной памяти в соответствии номеру подынтервала i, 
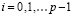. Для произвольного 
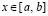номер подынтервала, которому принадлежит x, 
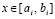, вычисляется как 
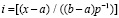, где [α] – целая часть числа α. Номер подынтервала – адрес обращения к памяти для считывания коэффициентов. После их считывания вычисление функции выполняется с использованием схемы Горнера за время
T = n(ty + tc), (9)
где ty – время бинарного умножения, tc – время бинарного сложения.
Методика определения числа подынтервалов и программная реализация метода. Следующая программа (Delphi), без изменений заимствованная из [4], реализует процесс преобразований (2) – (5) применительно к (6), (8):
program LagVarSigmaCiklSvertka7777777NIC1IDEALKOEFF28102022;
{$APPTYPE CONSOLE}
uses SysUtils;
const nn=25;hh=0.0000001*5;{hh=0.01*5;}tt=100000*5 {tt=1};
type vec=array[0..nn] of extended;vec0=array[0..nn,0..nn] of extended;
var n,i,j,k,l: integer; kk,rr: longint;
a,aa,b,bb, h, h1, x, s, s1, sk, bj,t: extended;
xx,dn: vec; z,d: vec0;
function f (x: extended): extended;
begin
f:=sin(x);
{f:=exp(-cos(x));}
{f:=exp(-1/sqr(x));}
end;
procedure ro(var n, j:integer; var z,d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0];
for k :=2 to n do
begin
e[k,k]:=e[k-1,k-1];
for l :=1 to k-1 do
e[k,k-l]:=e[k-1,k-l-1]-e[k-1,k-l]*z[j,k-1];
e[k,0]:=-e[k-1,0]*z[j,k-1];
end;
for l:=n downto 0 do
d[j,l]:= e[n,l];
end;
function gorner1 (var j: integer): extended;
var pp:extended;
begin
pp:=d[j,n];
for i:=n downto 1 do
pp:=pp*j+d[j,i-1]; gorner1:=pp;
end;
function gorner2 (var dn: vec; var t: extended): extended;
var p2:extended;
begin
p2:=dn[n];
for i:=n downto 1 do
p2:=p2*t+dn[i-1]; gorner2:=p2;
end;
begin
aa:=0{aa:=1/2};bb:=1;
kk:=0; rr:=0;
a:=aa;b:=a+hh;
while b<=bb do
begin
n:=2;
h:=(b-a)/n; h1:=h/33{ h1:=hh};
for j:=0 to n do xx[j]:=a+j*h;
for j:=0 to n do
for i:=0 to n-1 do
if i<j then z[j,i]:=i
else z[j,i]:=i+1;
for j:=0 to n do ro( n, j, z,d);
for l:=0 to n do
begin
sk:=0;
for j:=0 to n do
sk:=sk+f(xx[j])*d[j,l]/gorner1(j);
dn[l]:=sk;
{writeln (‘rr=’,rr,’ ‘,’l=’,l,’ ‘,dn[l]:2:20,’ ‘) ;}
end;
{writeln;writeln;}
x:=a{x:=a +0.0000001*2}{ x:=a +0.01*2};
while x <= b do
begin
t:=(x-xx[0])/h;
s:=gorner2 (dn, t);
kk:=kk+1;
if kk=tt then begin writeln;writeln (x,s,s-f(x)); kk:=0; end;
{writeln;writeln;}
x:=x+h1;
end;
rr:=rr+1;
a:=aa+rr*hh;b:=a+hh;
end;
readln;
end.
Степень полинома n может быть задана произвольно. В данном случае преобразования реализуются для n=2. Длина подынтервала hh задается пользователем в разделе констант: в данном примере hh=0.0000001*5. Для этой степени вычисление с коэффициентами (8) выполняет оператор s:=gorner2 (dn, t); В рассматриваемом варианте программы адрес номера подынтервала не вычисляется. В каждый подынтервал независимая переменная входит в цикле, где приближение проверяется по нескольким проверочным точкам с шагом h1:=h/33; Для априори заданной границы погрешности подбирается наибольшая возможная длина подынтервала hh, при которой погрешность приближения к заданной функции не выходит из границы во всех проверочных точках. Интерполируемая функция задается в подпрограмме
function f (x: extended): extended;
begin f:=sin(x); end;
Функция может быть любой реализуемой в языке программирования (для примера закомментированы {f:=exp(-cos(x));} и {f:=exp(-1/sqr(x));}, в данном варианте приближается sin(x)). Приближение выполняется на основном промежутке, который задается произвольно. В рассматриваемом случае [a, b] = [0, 1], в программной реализации aa:=0; bb:=1; Если при n = 2 требуется обеспечить границу абсолютной погрешности приближения f(x) = sin x на [0, 1] порядка 10–20 (такая же точность достигается для закомментированных функций), то, как это сделано в разделе констант, следует взять hh=0.0000001*5. При выбранных параметрах программы это означает, что требуемое число подынтервалов равно 2×106. В общем случае на каждом подынтервале для полинома степени n требуется n+1 коэффициентов, и суммарное по всем подынтервалам число коэффициентов составит (n+1)×p. В данном случае число коэффициентов 6×106. Предполагается располагать их в виде двумерного массива из n+1 столбцов и p строк. В рассматриваемом случае строки массива индексируются значениями переменной rr от 0 до 1999999, коэффициенты индексируются значениями l от 0 до 2. Вывод коэффициентов с индексными параметрами осуществляется по этой программе следующим образом. Счетчик выводимых значений следует задать tt=1 (вместо не закомментированного исходного значения). Вместо шага проверочных точек h1:=h/33; задается шаг, равный длине подынтервала h1:=hh; Вместо начального значения x:=a задаётся сдвинутое на любое число меньшее длины подынтервала значение, в данном случае x:=a +0.0000001*2. В цикле приведения подобных при равных степенях (при вычислении коэффициентов) for l:=0 to n do перед окончанием тела цикла задается оператор вывода writeln (‘rr=’,rr,’ ‘,’l=’,l,’ ‘,dn[l]:2:20,’ ‘); Все требуемые изменения отмечены в программе комментариями, которые следует снять. Наконец требуется снять скобки комментария с операторов пропуска пустых строк. В результате программа выведет все 6×106 коэффициентов с указанием их индексов. Если число коэффициентов не критично велико, их можно расположить непосредственно в разделе констант программы. С выполнением к ним адресации приближенное вычисление функции займет время (9), что в рассматриваемом случае составит время двух умножений и сложений. Методика выбора минимального объема требуемой памяти описывается на примере непосредственно ниже.
Пусть, например, требуется обеспечить границу абсолютной погрешности приближения f(x) = sin x на [0, 1] порядка 10–7 (с точностью до коэффициента). Программа запускается для hh=0.1. В результате работы программы по значению выводимой погрешности выясняется, что такой длины подынтервала недостаточно. Тогда задается hh=0.01. Это обеспечивает требуемую точность с избытком. Поэтому длину подынтервала можно увеличить, в частности до hh=0.05. Запуск программы с такими параметрами показывает, что искомая точность порядка 10–7 обеспечивается на всех подынтервалах. Это означает, что требуется 60 коэффициентов, которые можно расположить в разделе описаний констант как двумерный массив из 20 строк и 3 столбцов. Каждая строка соответствует номеру подынтервала, каждый коэффициент в строке – показателю степени слагаемого из полинома. Как только параметры определены, непосредственно вычисляются коэффициенты полинома, что реализуется раскомментированными операторами, как описано выше. Полученные коэффициенты имеют вид dd[rr,l], где rr – номер подынтервала, l – номер коэффициента, сопадающий с показателем степени слагаемого из полинома вида (8) на подынтервале. Далее строится простейшая программа, в которой коэффициенты располагаются в разделе констант. Адресоваться к ним следует с помощью операторов rr:=trunc((x-aa)/hh); a:=aa+rr*hh; b:=a+hh; В результате работы программы согласно (9) при n = 2 за время двух умножений и сложений вычислится синус от входного значения переменной. Программа имеет вид:
program LagVarSigmaSvertkaCiklAdr7777777DiapazonDJDJDJDJDJPravilno11;
{$APPTYPE CONSOLE}
uses SysUtils;
const aa=0;bb=1;hh=0.01*5;n=2;h=hh/n;
var x, s11,t: extended; i,rr: integer;
function f (var x: extended): extended;
begin f:= sin(x) end;
function SINUS (var x: extended): extended;
type vec0=array[0..19,0..2] of extended;
const dd:vec0=
((0.00000000000000000000, 0.02500520719408550000, -0.000007811279373170000),
(0.04997916927067833000, 0.02497395231605311000, -0.00002341431398910000),
(0.09983341664682815000, 0.02488027556341354000, -0.00003895882501400000),
(0.14943813247359922000, 0.02472441107926246000, -0.00005440595926573000),
(0.19866933079506122000, 0.02450674844363761000, -0.00006971710695338000),
(0.24740395925452293000, 0.02422783169977153000, -0.00008485399818160000),
(0.29552020666133958000, 0.02388835799426685000, -0.00009977879860548000),
(0.34289780745545135000, 0.02348917583459285000, -0.00011445420399664000),
(0.38941834230865049000, 0.02303128296825867000, -0.00012884353348441000),
(0.43496553411123021000, 0.02251582388896415000, -0.00014291082123888000),
(0.47942553860420300000, 0.02194408697596161000, -0.00015662090636677000),
(0.52268722893065917000, 0.02131750127377875000, -0.00016993952079533000),
(0.56464247339503536000, 0.02063763292035149000, -0.00018283337492470000),
(0.60518640573603956000, 0.01990618123249481000, -0.00019527024083453000),
(0.64421768723769105000, 0.01912497445849567000, -0.00020721903283706000),
(0.68163876002333417000, 0.01829596520844445000, -0.00021864988517508000),
(0.71735609089952276000, 0.01742122557372660000, -0.00022953422667082000),
(0.75128040514029270000, 0.01650294194787333000, -0.00023984485213899000),
(0.78332690962748339000, 0.01554340956171640000, -0.00024955599038561000),
(0.81341550478937375000, 0.01454502674650639000, -0.00025864336862251000));
function gorner11 (var rr: integer; const dd:vec0): extended;
var pp:extended;
begin
pp:=dd[rr,n];
for i:=1 to n do
pp:=pp*t+dd[rr,n-i]; gorner11:=pp;
end;
begin
if x<1 then rr:=trunc((x-aa)/hh) else rr:=trunc((x-aa)/hh)-1;
t:=(x-(aa+rr*hh))/h;
SINUS:=gorner11 (rr,dd);
end;
begin
x:= 1/21{ x:= 1/21 +hh+hh+hh+hh}{ x:= 19.8};
writeln (‘ ‘,’SINUS (x)=’,SINUS (x),’ ‘, ‘; ‘,’pogrechnost=’,SINUS(x)-f(x));
readln;
end.
Результат работы программы:
SINUS (x) = 4.76006258413486E-0002 ;
pogrechnost = -4.27201385477695E-0007
В общем случае соответствие количества коэффициентов границам абсолютной погрешности ε приближения функции коррелируется с данными приводимых ниже таблиц.
Программы с критично большим числом констант будут использовать хранение коэффициентов аппроксимирующих полиномов в виде типизированного файла.
Таблица 1
Количество констант для кусочно-интерполяционного вычисления функции sin x на [0, 1] при различных степенях полинома и различных границах погрешности
|
ε |
n=2 |
n=3 |
n=4 |
n=5 |
|
10-5 |
1.5·101 |
5 |
6 |
6 |
|
10-6 |
3·101 |
1·101 |
10 |
6 |
|
10-7 |
7.5·101 |
2·101 |
10 |
7 |
|
10-8 |
1.5·102 |
5·101 |
2·101 |
10 |
|
10-9 |
3.5·102 |
7.3·101 |
2.5·101 |
1.2·101 |
|
10-10 |
7.5·102 |
1.6·102 |
5.3·101 |
1.5·101 |
|
10-11 |
1.5·103 |
2·102 |
8.3·101 |
2.4·101 |
|
10-12 |
5·101 |
5·102 |
1.25·102 |
3·101 |
|
10-13 |
7.5·103 |
8·102 |
2·102 |
7.5·101 |
|
10-14 |
1.5·104 |
1.6·103 |
2.5·102 |
1·102 |
|
10-15 |
5·104 |
2·103 |
5.9·102 |
1.5·102 |
|
10-16 |
6·104 |
5·103 |
6.25·102 |
2.4·102 |
|
10-17 |
1.5·105 |
8·103 |
1.25·103 |
3·102 |
|
10-18 |
3·105 |
5·105 |
2.5·106 |
7.5·102 |
|
10-19 |
6·105 |
4·106 |
- |
- |
|
10-20 |
6·106 |
- |
- |
- |
Таблица 2
Количество констант для кусочно-интерполяционного вычисления функции tg x на [0, 1] при различных степенях полинома и различных границах погрешности
|
ε |
n=2 |
n=3 |
n=4 |
n=5 |
|
10-5 |
7.5·101 |
1·101 |
2.5·101 |
1·101 |
|
10-6 |
1.5·102 |
5·101 |
3.3·101 |
2.4·101 |
|
10-7 |
37.5·101 |
1·102 |
5·101 |
3·101 |
|
10-8 |
7.5·102 |
2·102 |
1·102 |
6·101 |
|
10-9 |
1.5·103 |
4·102 |
1.25·102 |
1·102 |
|
10-10 |
37.5·102 |
5·102 |
2.5·102 |
1.5·102 |
|
10-11 |
7.5·103 |
1·103 |
4.17·102 |
2.4·102 |
|
10-12 |
1.5·104 |
2·103 |
6.25·102 |
3·102 |
|
10-13 |
37.5·103 |
4·103 |
1·103 |
4·102 |
|
10-14 |
7.5·104 |
5·103 |
1.25·103 |
7.5·102 |
|
10-15 |
1.5·105 |
1·104 |
2.5·103 |
1·103 |
|
10-16 |
3.5·105 |
1.6·104 |
3.333·103 |
1.5·103 |
|
10-17 |
7.5·105 |
3.2·104 |
2.5·105 |
7.5·105 |
|
10-18 |
1.5·106 |
2·106 |
5·106 |
- |
|
10-19 |
6·106 |
4·106 |
- |
- |
|
10-20 |
- |
- |
- |
- |
Применение полинома Ньютона с равноотстоящими узлами интерполяции. При каждом i из (6) рассматриваемый интерполяционный полином Ньютона имеет вид
,
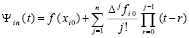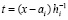, (10)
где узлы интерполяции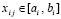 
, 
, 
, 
, 
, 
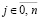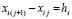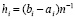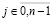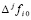– конечная разность j-го порядка в узле 
, 
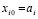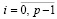, p из (6). Полином (10) на каждом подынтервале, аналогично полиному Лагранжа, можно преобразовать к виду алгебраического полинома с числовыми коэффициентами. Для этого каждый полином 
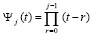из (10) преобразуется в полином с коэффициентами. Если положить tr = r, r ≤ j – 1, по схеме (4) получится
,
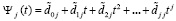где коэффициенты – целые числа. Почленное умножение таких полиномов на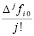 
в (10) повлечет развернутую форму полинома Ньютона
,
, 
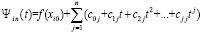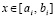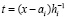, (11)
с вещественными коэффициентами. Если привести подобные в (11), то полином Ньютона примет вид
,
, 
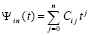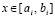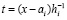. (12)
Программная реализация метода на основе полинома Ньютона с автоматическим выбором параметров. Программа, реализующая описанные выше преобразования, включает программный выбор параметров, обеспечивающих вычисление функции с априори заданной границей абсолютной погрешности. Пусть число подынтервалов p = 2k. Подбор k начинается с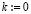 
для степени полинома 
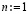, точность приближения проверяется во всех проверочных точках, при нарушении в какой-либо из них заданной границы погрешности выполняется переход к 
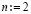и т.д. Оператор 
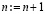выполняется в заданных границах n ≤ n0. При превышении границы числа подынтервалов выполняется переход к удвоенному числу подынтервалов 
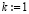с начальным значением показателя степени 
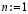и т.д. Оператор 
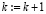выполняется в заданных границах k ≤ k0. Фиксируются наименьшие постоянные k и n, при которых граница погрешности не нарушается во всех проверочных точках:
program Varying_Piecewise_Interpolation_function_Newton_min_k; {$APPTYPE CONSOLE}
uses SysUtils;
const abs_error=1.0e-6; nn=20;
type M=array[0..nn] of extended; MM=array[0..nn,0..nn] of extended;
var n_min,k_min:byte;a0,b0:extended; d: MM; k_output:integer;
{const n_fix=2;
type Coeff = array[0..n_fix] of extended;
var f: file of Coeff; dd:Coeff;}
function u(x:extended):extended;
begin u:=sin(x) end;
procedure Konech_Raznoct(n:byte;a00,h: extended; var dy:MM); var i,k:byte;x:M;
begin for i:=0 to n do x[i]:=a00+i*h;
for i:=0 to n-1 do dy[1,i]:=u(x[i+1])-u(x[i]);
for k:=2 to n do for i:=0 to n-k do dy[k,i]:=dy[k-1,i+1]-dy[k-1,i] end;
procedure Viet(n:byte;var d:MM); var q:MM;k,i,j:byte;
begin q[1,1]:=1; q[1,0]:=0; for k:=2 to n do begin
q[k,0]:=-q[k-1,0]*(k-1); for i:=1 to k-1 do
q[k,k-i]:=q[k-1,k-i-1]-q[k-1,k-i]*(k-1); q[k,k]:=q[k-1,k-1] end;
for j:=1 to n do for i:=0 to j do d[i,j]:=q[j,i] end;
procedure pi_Newton(print:boolean;n,k:byte; var cond:boolean);
var xpr,t,hpr,s,p,h:extended; factorial:integer;flag:boolean;
dy: MM; a00, b00, vel_podint: extended; i, j, l: byte; b,y,a: M;kk, n_pod:int64;
begin
vel_podint:=(b0-a0)/exp(k*ln(2)); a00:=a0; b00:=a00+vel_podint; kk:=0;
n_pod:=0; flag:=true;
while a00<=b0-vel_podint do
begin
h:=(b00-a00)/n; hpr:=h/33; Konech_Raznoct(n,a00,h,dy); xpr:=a00;
while xpr<=b00 do
begin
t:=(xpr-a00)/h; factorial:=1;
for j:=1 to n do begin factorial:=factorial*j; b[j]:=dy[j,0]/factorial; end;
a[0]:=u(a00);
for l:=1 to n do
begin s:=0;
for j:=l to n do s:=s+d[l,j]*b[j];
a[l]:=s
end;
p:=a[n];
for i:=n-1 downto 0 do p:=p*t+a[i];
if print then
begin inc(kk);
if flag then
begin
writeln(‘n=’,n,’ n_pod=’,n_pod);
for i:= 0 to n do writeln(‘a[‘,i,’]=’,a[i]);
{for i := 0 to n_fix do dd[i]:=a[i];
write(f, dd);}
flag:=false;
end;
if kk=k_output then begin writeln(xpr,’ ‘,p,’ ‘,abs(p-u(xpr)));kk:=0;end;
end;
if abs(p-u(xpr))>abs_error then cond:=false;
xpr:=xpr+hpr
end;
a00:=a00+vel_podint; b00:=a00+vel_podint; n_pod:=n_pod+1;flag:=true;
end;
end;
procedure vpi_f(a0,b0:extended; var n_min,k_min:byte);
var n,k:byte; cond:boolean;
begin k:=0;
repeat n:=1;
repeat cond:=true; pi_Newton(false,n,k,cond);
if cond=true then
begin n_min:=n; k_min:=k; pi_Newton(true,n,k,cond);
writeln; writeln(‘n_min = ‘,n_min,’ k_min = ‘,k_min);
exit;
end
else n:=n+1;
until n>15;
k:=k+1
until k>17;
end;
begin
{AssignFile(f,’F:\sin.bin’);
Rewrite(f);}
k_output:=50;
a0:=0; b0:=1;
Viet(nn, d);
vpi_f(a0, b0, n_min, k_min);
{CloseFile(f);}
readln;
end.
Граница абсолютной порешности задается в разделе констант: abs_error=1.0e-6. Значение n_pod определяет номер подынтервала, a – массив коэффициентов полинома на подынтервале. Программа выводит номер подынтервала и значения коэффициентов полинома, соответствующих данному номеру. Затем строится программа, где зафиксированные коэффициенты задаются в разделе констант в виде двумерного массива:
program NewtonVarSigmaSvertkaCiklAdr7777777DiapazonDJDJDJDJDJPravilno6;
{$APPTYPE CONSOLE}
uses SysUtils;
const aa=0;bb=1;hh=1;n=5;h=hh/n;
var x, t: extended;
i,rr: integer;
function f (var x: extended): extended;
begin f:= sin(x) end;
function SINUS (var x: extended): extended;
type vec0=array[0..0,0..5] of extended;
const dd:vec0=
((0.00000000000000000000, 0.19999560375268066000, 0.00000975661575774000,
-0.00134093110346268000, 0.00000258073717352000, 0.00000232079291198000));
function gorner11 (var rr: integer; const dd:vec0): extended;
var pp:extended;
begin
pp:=dd[rr,n];
for i:=1 to n do
pp:=pp*t+dd[rr,n-i]; gorner11:=pp;
end;
begin
if x<1 then rr:=trunc((x-aa)/hh) else rr:=trunc((x-aa)/hh)-1;
t:=(x-(aa+rr*hh))/h;
SINUS:=gorner11(rr,dd);
end;
begin
x:=1/21;
writeln (‘ ‘,’SINUS (x)=’,SINUS (x),’ ‘, ‘; ‘,’pogrechnost=’,SINUS(x)-f(x));
readln;
end.
Результат работы программы:
SINUS (x) = 4.76004648918241E-0002 ; pogrechnost=-5.88150910031852E-0007
В рассмотренном частном случае получилось n = 5, массив коэффициентов оказался состоящим из одной строки. Полином 5-й степени выполняет вычисление синуса от произвольного аргумента на отрезке [0, 1] с точностью порядка 10–7 за время 5(ty + tc).
Реализация метода при помощи записи коэффициентов в файл. Еще один вариант программной реализации метода получается с использованием записи коэффициентов аппроксимирующих полиномов в типизированный файл, в котором они постоянно хранятся и откуда они считываются для последующего вычисления полинома по схеме Горнера. Для записи коэффициентов полиномов в файл в представленной выше программе Varying_Piecewise_Interpolation_function_Newton_min_k достаточно раскомментировать закомментированные части программы и удалить фрагмент:
writeln(‘n=’,n,’ n_pod=’,n_pod);
for i:= 0 to n do writeln(‘a[‘,i,’]=’,a[i]);
Программа вычисления функции с помощью считывания коэффициентов полиномов из файла примет следующий вид (в данном частном случае f(x) = sin x на [0, 1] приближается полиномом Ньютона степени n = 2 с погрешностью порядка 10–19):
program NewtonPravilnoSin_for_article; {$APPTYPE CONSOLE}
uses SysUtils;
const aa=0;bb=1; hh=3.81469726562500E-0006; n=2; h=hh/n;
var x, t: extended; i: integer; rr:int64;
function f (var x: extended): extended;
begin f:= sin(x) end;
function SINUS(var x: extended): extended;
type Coeff = array[0..n] of extended;
var f: file of Coeff; dd: Coeff;
function gorner11 (const dd:Coeff): extended;
var pp:extended;
begin pp:=dd[n]; for i:=1 to n do pp:=pp*t+dd[n-i]; gorner11:=pp; end;
begin
AssignFile(f,’F:\sin.bin’); Reset(f);
if x<bb then rr:=trunc((x-aa)/hh) else rr:=trunc((x-aa)/hh)-1;
seek(f,rr); read(f,dd);
t:=(x-(aa+rr*hh))/h; SINUS:=gorner11(dd);
CloseFile(f);
end;
begin
x:=0.23;
writeln (‘x= ‘,x,’ ; ‘,’SINUS(x)=’,SINUS(x),’ ‘, ‘; ‘,’pogrechnost=’,SINUS(x)-f(x));
readln;
end.
Результат работы программы:
x= 2.30000E-0001;
SINUS(x)= 2.27977523535188E-0001;
pogrechnost= 3.38813178901720E-0019
Файл sin.bin хранит коэффициенты, соответственные количеству подынтервалов p = 218, число коэффициентов составит 3×218. В результате обеспечивается вычисление синуса c погрешностью порядка 10–19 для произвольного аргумента из [0, 1] за время 2(ty + tc). При этом не учитывается время обращения к памяти, которое практически мало влияет на оценку временной сложности вычисления функции. Этот результат в принципе не достигается в предыдущем варианте с использованием раздела констант программы для хранения коэффициентов. Вариант с хранением коэффициентов в файле позволяет преодолеть ограничения объема памяти раздела констант и достигать максимальной точности вычисления с минимальной временной сложностью.
Предварительное обсуждение. Предложенное кусочно-интерполяционное вычисление функций с расположением массива коэффициентов в раделе описаний программы фактически реализуемо в пределах границы погрешности порядка 10–16. Для большей точности препятствием оказываются ограничения числа констант языка программирования (в Delphi – 2 Gb), вследствие которых становится невозможным резервировать требуемые границы больших массивов. Если такие границы резервировать близко к пределу, в компьютере может нарушаться правильность обращения к массиву коэффициентов на подынтервале. Тем не менее в означенных пределах границ погрешности получается расширяемая мобильная библиотека стандартных программ вычисления элементарных функций и их суперпозиций с минимальной временной сложностью. Мобильность заключается в том, что программы такой библиотеки устанавливаются на любом компьютере простым копированием с носителя. Расширяемость обеспечивается тем, что любую необходимую функцию можно включить в библиотеку на основе универсальности интерполяции: для требуемой функции достаточно задать function f (x: extended): extended; в случае полинома Лагранжа или function u(x:extended):extended; в случае полинома Ньютона. Вследствие универсальности интерполяции основной промежуток вычисления функции можно задавать произвольно в любой части действительной оси, входящей в область допустимых значений функции, однако здесь препятствием могут оказаться границы числового диапазона компьютера (так, для e100 нельзя говорить о точности приближения). Очевидна возможность адаптации метода для функции, области, границ памяти и времени вычисления согласно требованиям пользователя: достаточно воспользоваться представленными выше программами.
Если требуется точность приближения функции в пределах 10–17 – 10–20, существует возможность использовать хранение коэффициентов в виде типизированного файла, как описано в предыдущем пункте. Ценой более высокой точности вычисления станет некоторое замедление обращения к памяти: потребуется предварительное выполнение команд открытия файла, считывания коэффициентов, закрытия файла. Это, однако, существенно не отразится на временной сложности, хотя при хранении файла коэффициентов на внешнем носителе, в частности на flash-карте, эти операции зависят от быстродействия носителя. Программа сохранит мобильность в отмеченном смысле с той разницей, что копировать с носителя потребуется не только саму программу, но и непосредственно файл коэффициентов.
В аспекте актуальных приложений с минимизацией временной сложности наиболее целесообразно записывать требуемый массив коэффициентов в постоянные запоминающие устройства компьютера (ПЗУ). В этом случае алгоритм адресации к номеру подынтервала сохраняется, но его необходимо модифицировать для дешифрации адреса в ПЗУ.
Применение метода для вычисления специальных функций. На основе кусочной интерполяции с использованием интерполяционного полинома Ньютона, преобразованного к виду (12), может быть получено приближенное решение задачи Коши для системы обыкновенных дифференциальных уравнений. Построение метода, алгоритмизация представлены в [5], программная реализация – в [4]. В свою очередь, значения приближенного решения можно использовать для получения значения функции в узлах интерполяции. Построение интерполяционного полинома на этой основе и его последующее преобразование к виду (12) позволит выполнить все описанные выше варианты кусочно-интерполяционного вычисления функции, в частности с максимальной точностью и минимальной временной сложностью. Специфика предварительного решения на основе кусочно-интерполяционного полинома Ньютона состоит в том, что приближенное решение непрерывно на всём промежутке приближения [5], поэтому узловые значения для последующей интерполяции могут выбираться «имманентно» (как это делалось для априори заданной функции) без ограничения числа подынтервалов на любом отрезке приближения функции. Такое построение приближения функции позволит варьировать хранение коэффициентов в постоянной памяти, в разделе констант программы, в файле на различных носителях для адаптации к требованиям пользователя по точности и времени вычисления.
С другой стороны, рассматриваемое кусочно-интерполяционное решение задачи Коши непосредственно представляет решение в виде полиномов (12) с готовыми коэффициентами на каждом подынтервале, при этом система подынтервалов покрывает весь промежуток решения (полиномы непрерывно склеиваются на границах подынтервалов) [4; 5]. Непосредственно именно эти коэффициенты можно хранить в памяти, что позволит затем воспроизводить решение в любой точке за время (9). То же относится к функции, которая на входе метода задается как решение задачи Коши. Разница в том, что точность приближения решения априори варьировать труднее, чем для аналитически заданной функции.
Ниже представлено вычисление функции Бесселя на основе кусочно-интерполяционного решения дифференциального уравнения Бесселя. После сохранения полученных коэффициентов интерполяционных полиномов, значения функции Бесселя могут быть вычислены за время (9) в любой точке области определения.
Решение уравнения
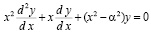(13)
на полуоси x > 0 при α ≥ 0 является функцией Бесселя первого рода Jα(x), которая в случае целочисленного значения α может быть представлена в виде
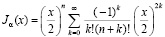[6].
В качестве примера выбрано кусочно-интерполяционное решение задачи Коши для уравнения (13) при α = 1 на отрезке [1, 2] по программе, представленной в [4]. Рассчитанные коэффициенты полиномиальных приближений после их сохранения позволяют приближать значения функции Бесселя первого рода единичного порядка J1(x) на отрезке [1, 2] с погрешностью порядка 10–18 в любой точке отрезка приближения за время 9(ty + tc). При этом число хранимых в памяти коэффициентов равно 40. Программа вычисления функции имеет вид:
program NewtonPravilnoBessel_for_article; {$APPTYPE CONSOLE} uses SysUtils;
const aa=1; bb=2; hh=0.25; n=9; h=hh/(n-1); J1_exact= 0.521501858460956878196;
var x, t: extended; i,rr: integer;
function BESSEL1 (var x: extended): extended;
type Coeff = array[0..n] of extended;
var f: file of Coeff; dd: Coeff;
function gorner11 (var rr: integer; const dd:Coeff): extended;
var pp:extended;
begin pp:=dd[n]; for i:=1 to n do pp:=pp*t+dd[n-i]; gorner11:=pp; end;
begin
AssignFile(f, ‘S:\Bessel.bin’); Reset(f);
if x<bb then rr:=trunc((x-aa)/hh) else rr:=trunc((x-aa)/hh)-1;
seek(f,rr); read(f,dd); t:=(x-(aa+rr*hh))/h; BESSEL1:=gorner11(rr,dd); CloseFile(f);
end;
begin
x:=1.25+1/21;
writeln (‘x= ‘,x,’ ; ‘,’BESSEL1(x)=’,BESSEL1(x),’ ‘, ‘; ‘,’pogrechnost=’,BESSEL1(x)-J1_exact);
readln;
end.
Результат работы программы:
x= 1.29761904761905E+0000;
BESSEL1(x)= 5.21501858460957E-0001;
pogrechnost= 1.62630325872826E-0018
Для контроля погрешности приближения в качестве эталонного значения функции Бесселя первого рода единичного порядка принято значение, полученное в результате запроса BesselJ(1, 1.25+1/21) в базе знаний Wolfram|Alpha [7].
Замечание 1. В этой программе расстояние между узлами интерполяционных полиномов Ньютона рассчитывается как h=hh/(n-1) в связи с тем, что кусочно-интерполяционное приближение решения задачи Коши строится первоначально для функции правой части (производной от решения), а непосредственно приближение решения восстанавливается как первообразная от построенного полинома [4; 5].
Дополнительные замечания. Выбранное значение n в (8), (12) можно зафиксировать, положив n = const для всех функций библиотеки. Тогда временная сложность вычисления (9) любой функции становится постоянной: T = const. Не умаляя общности, в этом случае можно считать, что время вычисления любой функции библиотеки имеет единичный порядок: T = O(1). Ввиду фактически малого значения постоянной n алгоритм вычисления по схеме Горнера вычислительно устойчив – не влечет накопления погрешности с ростом n. В предложенном методе вычисления функции взаимно независимы по всем значениям аргумента. Это означает параллелизм метода по независимым переменным и по всем функциям библиотеки. Вследствие постоянства n очевидна возможность синхронизации параллельных процессов вычисления всех функций во всех заданных точках. Тогда оценку (9) можно отнести к синхронному параллельному вычислению множества функций на множестве готовых значений аргументов. Необходимо отметить особенность метода для численного моделирования физических процессов. В силу постоянно хранимых коэффициентов любая функция библиотеки может многократно (и параллельно) воспроизводиться на произвольном множестве точек из области допустимых значений. Аналогично это относится к функциям, которые являются решениями задачи Коши для системы дифференциальных уравнений – однократное решение системы позволяет в дальнейшем хранить коэффициенты кусочной интерполяции и воспроизводить (в частности, параллельно) решение на любом множестве точек (без повторного численного интегрирования) за время (9). Для различных начальных значений процесс воспроизведения тривиально распараллеливается. Отмеченные особенности важны, в частности, при использовании численного моделирования с помощью дифференциальных уравнений с целью предсказания координат движущихся космических объектов в заданный промежуток времени. Если при этом функции правых частей уравнений вычислять с помощью предложенной библиотеки стандартных программ, то процесс численного моделирования ускоряется пропорционально n и числу функций, а точность приближения существенно превосходит стандартные требования [8]. Аналог метода для функций двух переменных рассмотрен в [9]. От известных методов разработки библиотек стандартных функций [10; 11] предложенный метод отличается по построению, достижением максимальной точности (в пределах числового диапазона языка программирования) вычисления функций при минимальной временной сложности, инвариантностью, единством структуры и однородностью вычислительных алгоритмов.
Заключение
Изложено кусочно-интерполяционное вычисление функций одной вещественной переменной в качестве основы расширяемой библиотеки стандартных программ. Представлены программы вычисления коэффициентов аппроксимирующих полиномов в соответствии номерам подынтервалов кусочной интерполяции. Рассмотрены варианты хранения коэффициентов в разделе констант программы, в типизированном файле, в постоянном запоминающем устройстве, дан алгоритм считывания. С точностью до времени обращения к памяти время вычисления функции определяется из (9), где n – степень интерполирующего полинома. Показана эффективность программной реализации метода. Конструктивно достигается максимальная точность приближения функций при одновременной минимизации временной сложности. В частности, функция вычисляется за время O(1) при точности приближения порядка 10–19. Отмечается широта области и простота применения библиотеки стандартных программ на предложенной основе.
Библиографическая ссылка
Ромм Я.Е., Джанунц Г.А., Медведкин Н.А. О БИБЛИОТЕКЕ СТАНДАРТНЫХ ПРОГРАММ ВЫЧИСЛЕНИЯ ФУНКЦИЙ НА ОСНОВЕ КУСОЧНОЙ ИНТЕРПОЛЯЦИИ // Современные наукоемкие технологии. – 2022. – № 11. – С. 57-70;URL: https://top-technologies.ru/ru/article/view?id=39397 (дата обращения: 20.04.2024).