Проблемой вычисления определенных интегралов от функций, не имеющих первообразных, начали заниматься еще в XVII в., когда немецкий и английский ученые Г. Лейбниц и И. Ньютон открыли основные принципы дифференциального и интегрального исчислений. В этот период решались задачи астрономии, геодезии и расчета механических конструкций. С 1940 г. потребность в численных методах возросла в связи с решением военных задач, требующих высокой скорости и определенной точности. Существуют более 10 методов численного интегрирования [1], однако наш интерес представляют методы Ньютона – Котеса, так как эти методы можно реализовать в среде программирования. Часто встречаются функции, первообразную от которых найти невозможно, следовательно, невозможно использовать знаменитую формулу Ньютона – Лейбница. Решением данной проблемы выступают численные методы интегрирования: метод прямоугольников, метод трапеций, метод Симпсона. Наиболее часто неберущиеся функции встречаются в физических задачах, в разделах статистической физики, оптики и термодинамики.
Использование информационных технологий находит свое применение во многих сферах образования. При решении задач по физике вычисление определенных интегралов зачастую вызывает у студентов затруднения, что ведет к временным затратам и потере точности. Интеграция таких дисциплин, как физика, математика и информатика, в цифровой среде повышает эффективность решения задач. Использование открытого кода и возможность модификации программ мотивирует студентов к изучению языка программирования Python.
Целью работы является программная реализация численных методов интегрирования на языке Python и их адаптация для решения физических задач в процессе преподавания дисциплин естественнонаучного направления бакалаврам.
Материалы и методы исследования
Исследование проводилось в процессе подготовки бакалавров педагогического и инженерного направлений. В исследовании рассмотрены следующие методы численного интегрирования: метод прямоугольников, метод трапеций, метод Симпсона. В данных методах используется геометрический смысл определенного интеграла. То есть интеграл представляет собой площадь, которая ограничена кривой y = f(x), осью OX и прямыми x = a, x = b. Метод численного интегрирования заключается в замене подынтегральной функции вспомогательной (аппроксимирующей) функцией, интеграл от которой вычисляется в элементарных функциях.
Самым простым методом численного интегрирования является метод прямоугольников. Существует три способа использования данного метода: метод левых прямоугольников, метод правых прямоугольников и метод средних прямоугольников [1].
Метод трапеций также относится к простейшим методам численного интегрирования, но дает значительно лучшее приближение. Также, в отличие от метода прямоугольников, метод трапеций применим к функциям, заданным в конечном числе точек, так как в этом случае всегда можно взять в качестве узлов интегрирования данные точки [2]. Метод трапеций встречается на практике чаще, чем метод прямоугольников, но реже, нежели метод Симпсона. Метод Симпсона приближенного вычисления определенного интеграла основан на замене графика подынтегральной функции дугами парабол, оси которых параллельны оси OY [1]. То есть, если заменить подынтегральную функцию квадратичной функцией, то, вычислив определенный интеграл от нее на заданном отрезке, получим формулу Симпсона [2]. В отличие от предыдущих методов, в методе Симпсона аппроксимирующая функция гладкая, поэтому погрешность данного метода ниже, чем в методах левых и правых прямоугольников и в методе трапеций.
Результаты исследования и их обсуждение
Численные методы интегрирования встроены во многие математические пакеты, однако есть ряд причин, по которым использование написанных программ имеет преимущество среди математических пакетов. Одна из основных – это то, что точность вычисления в математических пакетах по проведенному анализу оказалась ниже, чем точность алгоритмов, реализованных на языке Python.
В результате работы перечисленные выше методы были реализованы на языке программирования высокого уровня Python [3] и представлены в виде веб-ресурса, разработанного на основе фреймворка Django. Django – это свободный фреймворк для веб-приложений на языке Python, использующий шаблон проектирования MVC (Model-View-Controller) [4]. На сегодняшний день это довольно современный фреймворк, с его помощью написаны такие сайты, как Instagram, Disqus, Mozilla, The Washington Times, Pinterest, YouTube, Google и многие другие. Django предлагает высокий уровень производительности за счет встроенных шаблонов. Данный фреймворк может легко взаимодействовать с клиентской структурой и предоставлять контент практически в любом формате. Сценарии использования ресурса представлены на рис. 1.
В данных сценариях описаны действия пользователя, которые он может совершать на сайте. По рис. 1 видно, что при открытии сайта пользователь переходит в раздел навигации, то есть меню сайта. Из меню сайта он может выбрать онлайн подсчет интеграла одним из трех методов или воспользоваться пунктом меню «код программ».
При переходе в один из этих пунктов пользователь видит формы для ввода своих значений (рис. 2), всего на каждой странице метода по три формы для ввода. Каждая форма подписана, поэтому ввод данных будет не затруднителен.
Страница с кодом программ позволяет не только просматривать использованный алгоритм методов Ньютона – Котеса, но и копировать представленный код для расчетов других функций вне веб-ресурса. Для того чтобы использовать данный код, пользователю достаточно скопировать код из формы и воспользоваться компилятором Python, например онлайн-компилятором.
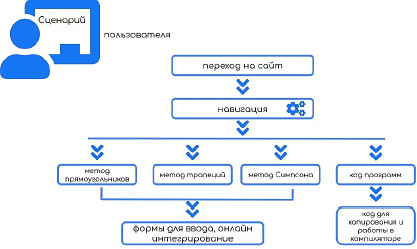
Рис. 1. Пользовательские сценарии
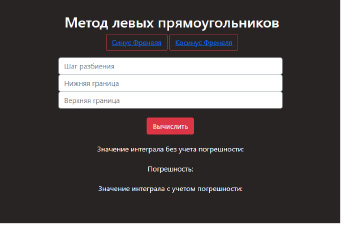
Рис. 2. Формы для подсчета определенных интегралов
На страницах сайта уже представлены формы для подсчета неберущихся определенных интегралов физических функций: интегралы Френеля, функция Пуассона, функция обратного логарифма, дополнительные интегралы Френеля [5, 6].
Стоит подробнее остановиться на проблемных физических задачах, представленных в ресурсе. В задачах по оптике при описании явлений дифракции Френеля в ближней зоне, возникает необходимость вычисления следующих интегралов:
.
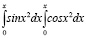Эти интегралы носят названия интегралы Френеля [5].
Проблемы, возникающие при изучении дифракционных явлений, являются наиболее трудными, и в оптике их редко удается довести до строгого математического решения. В большинстве случаев, представляющих практический интерес, из-за математических трудностей приходится прибегать к приближенным методам.
При изучении интегралов Френеля обычно их вычисляют с помощью контурного интегрирования комплексной плоскости. Суть этого метода заключается в представлении суммы этих интегралов комплексным числом, при этом применяя формулу Эйлера. Данный метод довольно известный и применимый, однако вычисление интегралов таким способом требует знаний не только методов вычисления определенных интегралов, но и теории функций комплексных переменных. Интегралы Френеля используются не только в задачах на дифракцию, в настоящее время с их помощью проектируются дороги, поэтому большой интерес они представляют не только для физиков, но и для инженеров [6].
К функциям f(x) = sin x2 и f(x) = cos x2 можно применить методы численного интегрирования. В задачах на поиск амплитуды волны в определенной точке поверхности, принято ею считать вектор, соединяющий левый и правый фокусы спирали Корню. Спираль Корню в свою очередь представлена интегралами Френеля, которые в частности берутся в пределах от 0 до ∞. Рассмотрим следующую задачу:
Построить спираль Корню, чтобы рассчитать распределение поля при дифракции Френеля [5].
Решение
Спираль Корню дает возможность качественно и количественно описать результат дифракции плоской волны, наблюдаемой на экране.
Чтобы построить данную спираль, в качестве декартовых координат берут значения
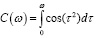и 
,
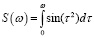где ω – параметр спирали Корню (рис. 3).
Центр спирали Корню – это центр дифракционной картины. Параметр спирали Корню – это отражение сдвига точек волны относительно центра влево и вправо. Далее выбираются значения ω (рис. 3) и вычисляются интегралы.
Значение интегралов Френеля при ω стремящейся к бесконечности были вычислены путем контурного интегрирования, их значения равны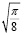 
.
Вычислим эти интегралы с помощью численных методов интегрирования и убедимся в том, что реализованные алгоритмы дают верное решение этой задачи.
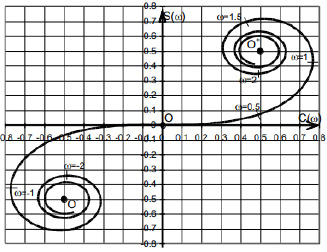
Рис. 3. Спираль Корню
С помощью написанных программ вычислим интегралы Френеля методом прямоугольников. Как правило, чтобы добиться уже предельного значения центральных координат спирали Корню, достаточно использовать шаг разбиения 100, верхнюю границу, равную 10, и нижнюю границу, равную 0 (рис. 2).
В результате вычислений получили значения интегралов равные 0,627 (произведено округление до тысячных). При сравнении полученного значения с числовым значением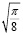 
, которое является достоверным и давно доказанным, можно сделать вывод, что численный метод интегрирования решает задачу нахождения неберущегося интеграла Френеля. Таким образом, становится возможным найти множество точек для построения Спирали Корню, для этого достаточно лишь уменьшать параметр ω (верхнюю границу интегрирования).
В задачах по термодинамике часто встречается задача на вычисление работы газа при изотермическом процессе. Графиком изотермического процесса является график гиперболы.
Рассмотрим следующую задачу:
Какую работу совершает водород при изотермическом расширении, если его объем увеличился с 1 л до 5?
Решение
Зная, что график изотермического расширения водорода выглядит как гипербола, нужно найти площадь криволинейной трапеции.
То есть вычислить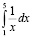 
.
Воспользуемся для этого численным методом трапеций, написанным на языке программирования Python и представленным в веб-ресурсе. Численное вычисление работы газа при увеличении объема с 1 до 5 л дает значение, равное 1,56.
Вычисление определенного интеграла в этом случае затрудняется точностью вычисления натурального логарифма, при использовании сервиса такая проблема отсутствует.
Из курса физики известна задача на вычисление массы стержня, когда дана функция плотности. Если стержень однородный, то значение массы вычислить намного проще, чем значение массы неоднородного стержня. Масса стержня на промежутке равна определенному интегралу от заданной функции и с пределами интегрирования, совпадающими с границами промежутка. Рассмотрим функцию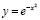 
, следовательно, массу найдем, вычислив 
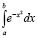. Интеграл является неберущимся, применив к вычислению метод Симпсона, реализованный в сервисе, можно найти массу стержня. Этот интеграл носит название интеграл Пуассона [5, 6], он встречается не только в физических задачах, но и в теории вероятности. Процесс вычисления интеграла Пуассона очень трудоемкий и зачастую дает неточный результат в силу погрешности параметров. В данном случае метод Симпсона является подходящим для интегрирования функций, первообразная которых не существует.
Для всех задач была выполнена проверка, вычисления соответствуют необходимой точности, путем сравнения полученных значений с эталонными и уже известными. Апробация ресурса проводилась в процессе обучения студентов бакалавриата по направлению «Педагогическое образование» профилей «Математика и физика», «Математика и информатика» и студентов инженерных направлений «Прикладная математика» и «Прикладная информатика» института информационных технологий и физико-математического образования Алтайского государственного педагогического университета. Двум группам студентов предлагалось решать задачи по физике, содержащие соответствующие интегралы с использованием ресурса, две группы выполняли практические работы без использования ресурса. Оценка эффективности ресурса была выполнена путем расчета среднего времени решения соответствующих задач и количества ошибочных решений. Время решения задач, содержащих интегралы Френеля, сократилось на 43 %, а задач, содержащих функцию Пуассона и функцию обратного логарифма, на 32 %. Количество задач с ошибочными решениями в целом уменьшилось на 27 %.
В процессе анкетирования по результатам применения ресурса студенты выделили следующие преимущества: ориентация ресурса на конкретные задачи; быстрое и точное вычисление одного и того же интеграла с различными параметрами; возможность доработки программ для вычисления интеграла произвольной функции. Ресурс не вызвал сложности в использовании у 92 % опрошенных студентов. После консультации со специалистами была отмечена перспективность представленной разработки, сейчас требуется методическая работа по подбору большего количества задачного материала. Дополнение ресурса задачами из различных дисциплин и расширение функционала позволит использовать ресурс более широко.
Заключение
В современной реальности компьютерная техника стала предметом повседневного использования человека, в связи с этим целесообразно применять ее образовательный потенциал, что эффективно скажется на учебном процессе. Использование разработанного веб-ресурса в обучении студентов позволяет не только быстрее и с большей точностью решать задачи, но и подчеркнуть важность межпредметных связей между такими дисциплинами, как «Физика», «Математический анализ» и «Численные методы».
Ресурс позволил снизить временные затраты на вычислительный процесс и повысить точность вычислений. В результате апробации была признана практическая значимость ресурса в образовательном процессе и возможность расширения функционала.
Рассмотренные задачи представляют интерес не только в научной сфере, но и в производственной. Преимущество программ численного интегрирования заключается в их универсальности, код программы подходит под любую функцию и может служить вспомогательным инструментом для преподавателей таких дисциплин, как «Физика», «Математическое моделирование», «Дифференциальное исчисление» и мн. др.
Библиографическая ссылка
Черпакова Н.А., Капустина Л.В. ИСПОЛЬЗОВАНИЕ ЧИСЛЕННЫХ МЕТОДОВ ИНТЕГРИРОВАНИЯ ПРИ РЕШЕНИИ ФИЗИЧЕСКИХ ЗАДАЧ В ПРОЦЕССЕ ПОДГОТОВКИ БАКАЛАВРОВ // Современные наукоемкие технологии. – 2022. – № 10-1. – С. 194-199;URL: https://top-technologies.ru/ru/article/view?id=39370 (дата обращения: 23.11.2024).