Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ананченко И.В. 1 Минчев Н.В. 1 Чумаков С.И. 1 Шишкевич М.В. 1

---

1 ФГБОУ ВО «Санкт-Петербургский государственный технологический институт (технический университет)»

Представлены фрагменты результатов наблюдений технологических режимов парогенератора и их анализ. Мониторинг парогенератора ДКВР-6.5-13 ГМ, управляемого автоматически системой управления «Факел-2010», осуществлялся сотрудниками научно-производственной организации «Уран-СПб». Система «Факел-2010» поддерживает стехиометрическое соотношение сжигаемого газа и воздуха. Фирмой «Уран-СПб» была поставлена задача найти дополнительные возможности для экономии газового топлива. С этой целью была проанализирована выборка, сформированная в процессе мониторинга. Объем выборки 500 записей, формат представления данных MS Excel. Сформулирован экономический критерий оптимальности. Экономический критерий оптимальности определяется как отношение расхода газового топлива к расходу питательной воды, подаваемой в барабан котла. Более правильно было бы брать отношение расхода газового топлива к расходу полученного пара, но так как точное измерение расхода пара вызывает технические сложности, то вместо расхода пара используется расход воды. Принято допущение, что вся подаваемая питательная вода преобразуется в конечном счете в пар. Построены линейная, квадратичная и кубическая оценки множественной функции регрессии для критерия оптимальности в зависимости от управляющих переменных, получены оценки корреляционной матрицы контролируемых параметров. После этого с учетом мультиколлинеарности проведено упрощение модели и найдены соответствующие режимы оптимального расхода газа в зависимости от нагрузки на парогенератор. Предложенная методика анализа может быть использована при управлении и более мощными промышленными парогенераторами.

Статья в формате PDF

527 KB

регрессионный анализ

оптимизация

энергосбережение

парогенератор

1. Парогенераторная установка. [Электронный ресурс]. URL: https://neftegaz.ru/tech-library/vspomogatelnye-ustroystva-i-instrument/142436-parogeneratornaya-ustanovka-pu/ (дата обращения: 09.08.22).

2. Наумов Н.Р., Марьяндышев П.А., Попов А.Н., Любов В.К. Исследование работы газовых котлов малой мощности // Технические науки. 2017. № 4. С. 27–33.

3. Плетнев Г.П. Автоматизация технологических процессов и производств в теплоэнергетике: учебник для студентов вузов. М.: МЭИ, 2016. 352 с.

4. Новиков О.Н., Окатьев А.Н., Чумаков С.И., Ананченко И.В., Шишкевич М.В. Оптимизация сжигания газового топлива в парогенераторе // Факторы и эффективные механизмы устойчивого развития / Под общ. ред. Г.Ю. Гуляева. Пенза: «Наука и Просвещение» (ИП Гуляев Г.Ю.), 2020. С. 102–125.

5. Шкаровский А.Л., Новиков О.Н., Новикова А.В., Полушкин В.Н. Разработка нового семейства интеллектуальных систем управления качеством сжигания топлива // Современные наукоемкие технологии. 2016. № 12. С. 556–561.

6. BelaG. Liptak Process control and optimization. Vol. 2. Boca Raton: Taylor&FrancisGroup, 2006, 2368 с.

7. Экспериментальные данные. Файл Выборка-исх. [Электронный ресурс]. URL: https://mctrewards.ru/Выборка-исх.xlsx (дата обращения: 09.08.22).

Парогенерирующая установка – комплекс оборудования для производства насыщенного пара, который применяется в качестве рабочего тела в паровых машинах, теплоносителя в системе отопления и в технологических процессах различных областей промышленности [1]. Данные установки являются одной из основных частей тепловых станций, которые являются основой электроэнергетики, так как занимают в данной области порядка 70 %. При выработке электроэнергии парогенератор выступает в качестве реакторной установки, предназначенной для производства пара, поступающего на турбогенератор для преобразования тепловой энергии в электрическую [1, 2].

В связи с современной тенденцией, направленной на экологию, в качестве основного вида топлива для топливосжигающих установок применяют газообразные виды топлива. Другой современной тенденцией является эффективное использование ресурсов, поэтому в качестве топлива пытаются использовать попутный газ, получаемый при добыче нефти, в особенности в населенных пунктах, располагающихся вблизи добывающих платформ [2].

Так как ресурсы, применяемые для работы топливосжигающих установок, являются медленно возобновляемыми или невозобновляемыми, а цена на них возрастает с каждым годом, то встает задача поиска дополнительных возможностей для экономии газового топлива. Одно из решений данной задачи основано на минимизации экономического критерия оптимальности, который можно определить как отношение расхода газового топлива к расходу получаемого пара. Однако вследствие того, что измерение расхода пара с точностью, необходимой для корректировки работы оборудования, связано с техническими сложностями, то вместо расхода пара предлагается использовать расход питательной воды. При этом предполагается, что вся питательная вода, подаваемая в парогенератор, будет преобразована в пар [3]. Используя предложенный критерий оптимальности, описана методика поиска благоприятного решения в зависимости от паровой нагрузки.

Парогенерирующие установки также применяются в современных тепловых сетях, поэтому актуальность решения данной задачи становится выше, особенно для тепловых станций, построенных в районах Крайнего Севера и в арктических регионах, так как на данных территориях особенно высоко потребление тепловых ресурсов. При рациональном сжигании топлива можно получить большой экономический эффект [3–6]. Хотя опубликован достаточно большой объем литературы по разработке, исследованию и принципам работы топливосжигающих установок, в частности есть учебные пособия [3] по парогенераторам, однако вопросы эффективного расходования и экономии ресурсов недостаточно проработаны [4].

С учетом актуальности задачи была сформулирована цель исследования: рассмотреть и проанализировать данные мониторинга на промышленном парогенераторе ДКВР-6.5-13 ГМ (табл. 1) для поиска оптимальных режимов его эксплуатации, с учетом предложенного критерия оптимальности – отношения расхода газа к расходу питательной воды, подаваемой в барабан котла. Таким образом, целевая функция здесь – это зависимость отношения расхода газа к расходу питательной воды, поступающей в барабан котла, от управляющих параметров в процессе образования пара. Задача – найти значения этих параметров, минимизирующих данную функцию. Результаты исследований могут иметь практическую значимость, в частности, при решении задач планирования деятельности предприятий топливно-энергетического комплекса.

Материалы и методы исследования

По данным мониторинга, предоставленным авторам руководством фирмы Уран-СПб, проведены оценки регрессионных поверхностей критерия в зависимости от управляемых переменных. Данные реального процесса, отсчет велся через каждую минуту. Всего анализировалось 500 отсчетов, данные можно скачать по ссылке [7]. Была поставлена задача найти дополнительные возможности для экономии газового топлива. Для решения поставленной задачи по предоставленным данным построены три модели поверхности множественной регрессии.

Рассматриваемый парогенератор управляется системой «Факел 2010», разработанной фирмой Уран-СПб. Параметры, контролируемые в ходе мониторинга, представлены в табл. 1. В таблице представлен диапазон изменения значений параметров, измеряемых в ходе мониторинга, приведены буквенные обозначения и размерности параметров, используемые фирмой Уран-СПб. В ходе анализа рассматривался 31 дискретный случайный процесс с дискретным временем. Необходимо было построить вероятностные модели и затем, используя сформулированный критерий оптимальности, выбрать наиболее целесообразный, с учетом результатов анализа, метод нахождения оптимума, после чего выполнить нахождение оптимума на основе имеющихся исходных данных.

На рис. 1 и 2 приведены графики фрагментов реализаций случайных процессов – расхода питательной воды, подаваемой в барабан котла и расхода газа, которые являются определяющими для расчета критерия оптимальности.

Из графиков видно, что частота колебаний расхода газа превосходит частоту колебаний расхода воды, что связано с особенностями системы управления «Факел 2010». На рис. 3 показана реализация поведения выбранного критерия оптимальности F = Fг/Fв.

Было установлено [4], что колебания критерия происходят в диапазоне от 3.08 до 11.91, а отношение максимального значения к минимальному составляет 3.9, что дает основания искать наиболее экономичные режимы парообразования. В ходе выполнения анализа было выявлено, что критерий оптимальности зависит от множества параметров, но большинство из них остаются постоянными и их можно исключать из рассмотрения.

Таблица 1

Описание данных мониторинга – 31 параметр, контролируемый в процессе образования пара

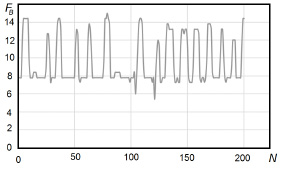
Рис. 1. График реализации случайного процесса расхода воды по первым начальным значениям от 1 до 200 (N – номер отсчета)

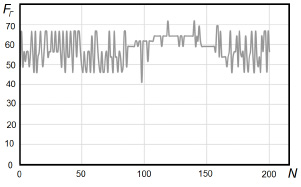
Рис. 2. График реализации случайного процесса расхода газа (N – номер отсчета)

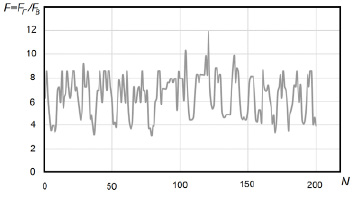
Рис. 3. Графическое представление реализации случайного процесса отношения расхода газа к расходу воды (N – номер отсчета)

В общем виде для поиска оптимального решения требуется отобразить пространство всех контролируемых переменных на множество значений критерия оптимальности. Отображение строится методом наименьших квадратов (МНК) в форме оценки множественной регрессии [4]. Однако в такой постановке размерность пространства параметров высока, и для практического решения требуется уменьшить эту размерность. Задачу можно упростить, выявив наиболее значимые управляющие параметры (в нашем случае выделено четыре таких параметра):

1. ИМП (х1) – положение заслонки, управляющей расходом воды (% открытия).

2. Fвент (х2) – частота оборотов вентилятора, подающего воздух на газовые горелки (Гц).

3. ИМГ (х3) – положение заслонки, управляющей расходом газа (% открытия).

4. Fдым (х4) – частота оборотов дымососа, создающего тягу в выхлопной трубе (Гц).

Два управляющих параметра – положение заслонок на воздух и дымосос – по 500 наблюдениям оставались неизменными, поэтому в расчет не принимались. Таким образом составлено уравнение для оценки функции регрессии в зависимости от четырех переменных. В ходе анализа выяснилось, что есть сильная корреляция между параметрами, что приводит к проблеме мультиколлинеарности. Чтобы избавиться от этой проблемы, задачу упростили.

Результаты исследования и их обсуждение

Была проведена оценка корреляционной зависимости всех параметров. В табл. 2 приведены оценки коэффициентов корреляции только управляющих параметров и выбранного критерия оптимальности F.

Таблица 2

Оценка корреляционной матрицы управляющих параметров и критерия оптимальности

На основе данных табл. 2 прослеживается сильная связь управляющих параметров: частоты вентилятора воздуха и частоты дымососа. Для упрощения задачи оптимизации можно исключить один из двух названных параметров. Кроме того, рекомендуется [4] исключать из уравнения регрессии сильно связанные между собой переменные с коэффициентом корреляции больше 0.7. Так как существует сильная связь между положением заслонки на газ и частотами вентиляторов, то можно оставить только два параметра. После упрощения задачи оставили переменные ИМП (х1) и ИМГ (х3), как переменные, не сильно коррелирующие друг с другом.

Для предлагаемой модели выполнена оценка коэффициента детерминации по формуле

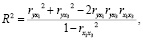
где 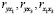– найденные оценки коэффициентов корреляции.

После подстановки в уравнение оценок коэффициентов корреляции, коэффициент детерминации принимает значение 0,66:

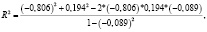
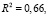
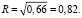
Из чего следует, что 34 % приходится на необъяснённую долю дисперсии, которая относится к факторам, исключённым из рассмотрения.

Рассматривалось три модели поведения функции регрессии в форме полиномиальной зависимости первого, второго и третьего порядков.

В табл. 3 представлены оценки дисперсий трех построенных моделей (линейная, квадратичная и кубическая).

Таблица 3

Сравнение предлагаемых полиномиальных моделей поведения функции регрессии

Так как регрессионные модели первого и второго порядка описывают функцию регрессии неудовлетворительно (сумма квадратов отклонений существенно больше, чем в третьем случае), то здесь приводятся оценки функции регрессии в пространстве двух управляющих переменных для кубической модели. Уравнение оценки кубической функции регрессии, полученное методом наименьших квадратов, имеет следующий вид:

.

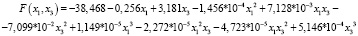Кроме того, оказалось, что эту кубическую модель можно дополнительно упростить. Примем значение коэффициента при 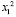равным 0. В данном случае это формулируется как основная гипотеза об адекватности упрощенной модели, которую проверили по критерию Фишера. Уравнение упрощенной кубической регрессии:

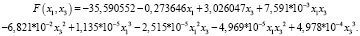
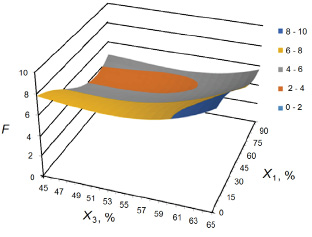
Рис. 4. Поверхность оценки функции регрессии

В табл. 4 приведены оценки дисперсий двух рассматриваемых моделей.

Таблица 4

Оценка предлагаемых кубических моделей оценки функции регрессии для критерия оптимальности

Расчет критерия Фишера F осуществлялся по формуле

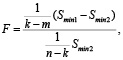
где k – число неизвестных параметров в уравнении регрессии полной кубической модели,

m – число неизвестных параметров в упрощенной модели,

n – объем выборки.

Вычислим это значение для k = 10, m = 9 и n = 500.

F = 0.033.

Критическое значение при уровне значимости α = 0.1 составляет 2.71, так как критерий F попал в область допустимых значений (существенно меньше критического значения), поэтому упрощенная модель нам подходит.

На рис. 4 представлена построенная поверхность оценки функции регрессии по упрощённой кубической модели.

Видно, что минимум находится в оранжевой области, на границе. Исходя из оценки функции регрессии, на рис. 5 представлен график зависимости минимального значения критерия от положения заслонки на питательную воду.

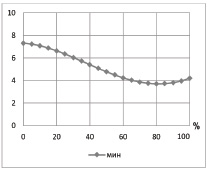
Рис. 5. График зависимости минимального значения критерия от паровой нагрузки (положения в % открытия заслонки на питательную воду – х1 )

Найдена зависимость (рис. 6) оптимального положения заслонки на газ в зависимости от паровой нагрузки (определяется положением заслонки на питательную воду х1). Дискретизация на графике обусловлена отсчетом цифрового преобразователя, поэтому приведенная для наглядности зависимость аппроксимируется кривой.

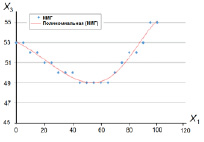
Рис. 6. График зависимости оптимального положения заслонки на газ от положения заслонки на питательную воду

Указанную зависимость можно использовать как в автоматическом, так и в ручном режиме управления процессом получения пара, для экономии топлива, что отвечает целевым установкам фирмы Уран-СПб [4].

Заключение

По предоставленным экспериментальным данным для системы управления «Факел 2010», впервые проведен анализ режимов работы парогенератора ДКВР-6.5-13 ГМ, решена задача поиска оптимальных режимов в зависимости от паровой нагрузки. Показано, что целесообразно в качестве регрессионной модели использовать параметрическую модель третьего порядка (существенно увеличивается точность аппроксимации). Найденные зависимости будут использоваться при модернизации системы управления «Факел 2010» на промышленном парогенераторе. Описанную методику анализа данных мониторинга можно использовать и на более высокопроизводительных тепловых станциях топливо-энергетического комплекса, что приведет к большому экономическому эффекту, что приведет к экономии газового топлива на уровне 5–10 %.

Библиографическая ссылка