Для повышения безопасности на дорогах, увеличения их пропускной способности, организации экономически выгодных маршрутов в сфере интеллектуальных транспортных систем стала развиваться технология Vehicle-to-Everything (V2X). V2X представляет собой коммуникацию, которая включает в себя связь между транспортными средствами, сетью, дорожной инфраструктурой и пешеходами. Так как V2X объединяет в себе множество видов коммуникации, стоит учитывать, что каждый отдельный элемент сети должен соответствовать требованиям качества обслуживания Quality of Service (QoS). Одними из основных требований выступают высокая пропускная способность и низкие задержки каналов связи. Для достижения этих характеристик в сети V2X необходимо грамотное распределение ресурсов [1].
Для достижения максимально эффективного распределения ресурсов в данной работе предлагается использовать методы глубокого машинного обучения, которые способны обрабатывать большой объем разнообразных данных. В области Vehicle-to-Everything методы машинного обучения имеют большой потенциал, и к ним проявляется соответствующий интерес. Рассмотрены методы машинного обучения, которые использовались и могут быть использованы в сетях V2X для оптимизации сетевого трафика путем эффективного распределения ресурсов внутри сети. Актуальность темы заключается в том, что существующие алгоритмы в сети Vehicle-to-Everything не решают проблемы распределения ресурсов внутри сети, и это является слабым местом технологии подключенных автомобилей. Методы машинного обучения могут помочь в решении этой проблемы. Объектом исследования является технология Vehicle-to-Everything. Предметом исследования являются методы машинного обучения.
Целью исследования является анализ моделей оптимизации трафика в сети Vehicle-to-Everything с помощью методов машинного обучения. В настоящее время глубокое обучение представляет собой передовой подход в задачах сложных беспроводных сетей. С помощью глубокого обучения решаются задачи управления, оптимизации сети, обнаружения аномалий и прогнозирования различных параметров. Рассматриваются модели, основанные на методе обучения с подкреплением в качестве решения проблемы распределения трафика в сетях V2X [2]. Основным отличием метода обучения с подкреплением от классических методов машинного обучения является то, что искусственный интеллект обучается в процессе взаимодействия с окружающей средой, а не на исторических данных. Системы, в которых может применяться обучение с подкреплением, называются Марковскими процессами принятия решения. Марковский процесс принятия решения предназначен для прямолинейной формулировки задачи обучения в результате взаимодействия агента и окружающей среды для достижения цели. Агентом называется сторона, которая обучается и принимает решения. Окружающая среда представляет собой все, с чем взаимодействует агент и все, что находится вне агента. Обе стороны взаимодействуют непрерывно. Агент выбирает действия, а среда реагирует на эти действия и предлагает агенту новые ситуации. Среда также генерирует вознаграждения, то есть числовые значения, которые агент стремится со временем максимизировать посредством выбора действий.
Описание системы. В сценарии коммуникации Vehicle-to-Everything каждая связь автомобиль-автомобиль (связь V2V) рассматривается как агент, а все, что находится за пределами этой связи, рассматривается как среда, которая представляет собой общее условие, связанное с распределением ресурсов (рис. 1).
Поскольку поведение других каналов V2V нельзя контролировать в децентрализованной среде, действие каждого агента (канала V2V) основано на общих условиях среды, таких как спектр или мощность передачи данных. В каждый момент времени (t) звено V2V в качестве агента наблюдает состояние (St) из пространства состояний S и выполняет соответствующее действие (at) из пространства действий A, выбирая поддиапазон и мощность передачи на основе политики (π). Политика принятия решений (π) может быть определена функцией состояния-действия, также называемой Q-функцией Q(St,at), которая может быть аппроксимирована с помощью глубокого обучения. В зависимости от действий агентов среда переходит в новое состояние St+1, и каждый агент получает вознаграждение rt от среды. В случае с автомобильной сетью вознаграждение определяется пропускной способностью каналов V2I и V2V и ограничениями задержки соответствующего канала V2V.
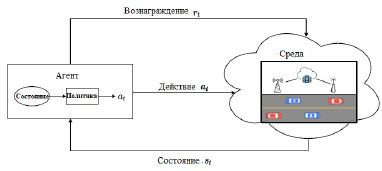
Рис. 1. Схема обучения с подкреплением для Vehicle-to-Everything сети
Состояние среды, наблюдаемое каждым соединением V2V, состоит из нескольких частей:
− Мгновенная информация о канале соответствующей линии V2V (Gt).
− Предыдущая мощность помех в линии (It-1).
− Информация о соединении V2I, например, от передатчика V2V к базовой станции (Ht).
− Выбранный подканал соседей в предыдущем временном интервале (Nt-1).
− Оставшееся время, необходимое для соблюдения ограничений по задержке (Ut).
Таким образом, состояние может быть выражено по формуле
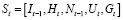 . (1)
. (1)
В каждый момент времени агент выполняет действие (at), которое состоит в выборе подканала и уровня мощности для передачи на основе текущего состояния (St), следуя политике (π).
Решение задачи оптимизации. Цель распределения ресурсов V2V заключается в следующем: агент (соединение V2V) выбирает полосу частот и уровень мощности передачи, которые позволят передавать данные, при этом сохраняя достаточно ресурсов, чтобы соответствовать требованиям ограничения задержки. Суммарная пропускная способность каналов V2I и V2V используется для измерения помех каналам V2I и другим каналам V2V соответственно. Сама функция вознаграждения состоит из трех частей:
− Пропускной способности каналов V2I.
− Пропускной способности каналов V2V.
− Условия задержки.
Функция вознаграждения выражается формулой
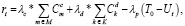 (2)
(2)
где T0 – максимально допустимая задержка, а λc, λd и λp – веса трех частей, так как мощность передачи дискредитируется по трем уровням [2].
Емкость пользователей мобильной сети выражается по формуле
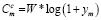 , (3)
, (3)
где W – пропускная способность канала, а ym – соотношение сигнал/шум (SINR) для пользователя мобильной сети.
Емкость пользователей V2V сети рассчитывается по формуле
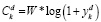 . (4)
. (4)
Чтобы добиться хороших результатов в долгосрочной перспективе, следует учитывать как немедленные, так и будущие вознаграждения. Таким образом, основная цель обучения с подкреплением состоит в том, чтобы найти политику, позволяющую максимизировать функцию вознаграждения. Это можно сделать с помощью формулы
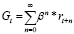 , (5)
, (5)
где β ϵ [0, 1] является коэффициентом вознаграждения
Переход состояния и вознаграждение являются стохастическими процессами и моделируются как марковский процесс принятия решений, где вероятность зависит только от состояния среды и действия, предпринятого агентом. Переход от St к St+1 с вознаграждением rt при совершении действия at можно охарактеризовать условной вероятностью перехода p(st+1, rt|st, at).
Создание нейронной сети. Глубокое Q-обучение используется для создания нейронной сети на основе подхода агент-действие. Агент предпринимает действия на основе политики π, которая представляет собой отображение пространства состояний S в пространство действий A, выраженное как π: St ϵ S → at ϵ А. Как указывалось ранее, пространство действия охватывает два измерения: уровень мощности и поддиапазон спектра, а действие at соответствует выбору уровня мощности и спектра для каналов V2V. Алгоритмы Q-обучения можно использовать для получения оптимальной политики для максимизации долгосрочного ожидаемого накопленного вознаграждения Gt [3]. Значение Q для данной пары состояние-действие (St, at), Q(St, at) политики π определяется как ожидаемое накопленное вознаграждение при выполнении действия at и последующем соблюдении политики π. Следовательно, значение Q можно использовать для измерения качества определенного действия в данном состоянии. Как только заданы Q-значения Q(St, at), можно легко построить улучшенную политику, предприняв действие, заданное формулой (6), которая описывает, что необходимо предпринять действие, которое максимизирует значение Q.
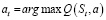 . (6)
. (6)
Оптимальную политику Q* можно найти без каких-либо знаний о динамике системы на основе уравнения обновления, представленного на формуле
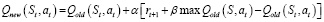 . (7)
. (7)
В сценарии распределения ресурсов, как только оптимальная политика будет найдена путем обучения, ее можно использовать для выбора полосы спектра и уровня мощности передачи для каналов V2V, чтобы максимизировать общую пропускную способность и обеспечить ограничения задержки для каналов V2V.
Классический метод Q-обучения можно использовать для поиска оптимальной политики, когда пространство состояний-действий невелико, где может поддерживаться таблица поиска для обновления значения Q каждого элемента в пространстве состояний-действий. Однако классическое Q-обучение не может быть применено, если пространство состояний-действий становится огромным, как в управлении ресурсами для связи V2V. Причина в том, что большое количество состояний будет посещаться нечасто, а соответствующее значение Q будет редко обновляться, что приведет к гораздо большему времени сходимости Q-функции [4]. Чтобы решить эту проблему, глубокая Q-сеть улучшает Q-обучение, объединяя глубокие нейронные сети с Q-обучением. Q-сеть обновляет свои веса на каждой итерации, чтобы минимизировать следующую функцию потерь, полученную из той же Q-сети со старыми весами в наборе данных. Функция потерь всегда считается важной частью алгоритмов глубокого обучения с подкреплением, потому что она строит мост через разрыв между Q-сетью и целевой сетью. Функция потерь DQN определяется по формуле (8).
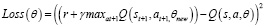 , (8)
, (8)
где y можно найти по формуле
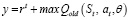 . (9)
. (9)
Для получения еще более производительной и стабильной нейронной сети в работе рассматривается вариант реализации двойной глубокой Q-сети [5]. Проблемой обычной DQN является то, что как выбор действия, так и оценка выбранного действия используют максимальное значение Q, что может привести к чрезмерно оптимистичной оценке значения Q. В частности, производительность алгоритма глубокой Q-сети ухудшается, если переоценка не будет происходить равномерно.
Чтобы решить проблему переоценки, целевое значение в двойной глубокой Q-сети выражается по формуле (10).
Из формулы (10) следует, что выбор действия отделен от генерации целевого значения Q. Этот простой прием позволяет значительно уменьшить переоценку, а процедура обучения выполняется быстрее и надежнее.
В двойной глубокой Q-сети выбор действия в функции argmax также зависит от значения веса θ. Это означает, что, как и в обычной Q-сети, оценка жадной политики также происходит в соответствии с текущим значением θ. Однако в этом подходе используется второй набор весов θd, чтобы можно было справедливо определить ценность политики. Второй набор весов может быть обновлен симметрично путем переключения ролей θ и θd.
Функция потерь для двойной DQN определяется по формуле (11).
Следующая и последняя модель нейронной сети будет основана на архитектуре дуэльного DQN [5]. Идея такой архитектуры заключается в том, что не всегда нужно определять ценность каждого доступного действия. В некоторых состояниях выбор действия не влияет на происходящее. Дуэльный алгоритм предсказывает отдельно средневзвешенное значение Q-функции – V(s), а не значение Q для всех действий. Также алгоритм предсказывает для каждого действия преимущество, которое определяется как разность между Q-функцией и средневзвешенным значением, как показано в формуле (12).
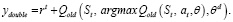 (10)
(10)
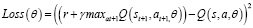 . (11)
. (11)
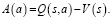 (12)
(12)
Здесь V(s) – это функция ценности, которая показывает, насколько хорошо находиться в данном состоянии s. A(a) – это функция преимущества, которая измеряет относительную важность определенного действия по сравнению с другими действиями. После того, как V(s) и A(a) вычисляются отдельно, их значения объединяются обратно в единую Q-функцию на конечном уровне. Это улучшение привело бы к улучшению оценки политики. Поскольку дуэльная архитектура использует тот же интерфейс ввода-вывода, что и стандартная архитектура DQN, процесс обучения идентичен. Функция потери для такой сети определяется по формуле
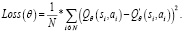 (13)
(13)
На этапе обучения используется глубокое Q-обучение на основе приобретенного моделью опыта, при котором обучающие данные генерируются и сохраняются в памяти. На каждой итерации мини-пакет данных выбирается из памяти и используется для обновления весов глубокой Q-сети. Политика, используемая в каждом звене V2V для выбора спектра и мощности, вначале является случайной и постепенно улучшается с помощью обновленных Q-сетей. На этапе тестирования выбираются действия в связях V2V с максимальным Q-значением, заданным обученными Q-сетями, на основе которых получается оценка. Поскольку действие выбирается независимо на основе локальной информации, агент не будет знать о действиях, выбранных другими связями V2V, если действия обновляются одновременно. Как следствие, состояния, наблюдаемые каждой связью V2V, не могут полностью характеризовать среду. Чтобы смягчить эту проблему, агенты настроены на асинхронное обновление своих действий, при этом только одна или небольшое подмножество связей V2V будут обновлять свои действия в каждый временной интервал. Таким образом, изменения среды, вызванные действиями других агентов, будут наблюдаемы.
В качестве результатов работы модели рассматриваются графики зависимости среднего значения функции потерь (L) к количеству пройденных эпох и нормированные графики зависимости среднего значения вознаграждения (Q) к количеству пройденных эпох. На рис. 2 представлено сравнение графиков зависимости функции потери от количества эпох для всех трех моделей.
На рис. 2 показан график сходимости функции потерь, используемой для каждой сети DQN. Из графика видно, что значение функции потерь уменьшается в ходе обучения каждой модели, что говорит о том, что все три модели действительно обучаются с каждой новой итерацией. При этом, рассматривая поведение функции потери для каждой реализованной модели, можно заметить, что лучшее значение функции потерь показывает двойная DQN модель.
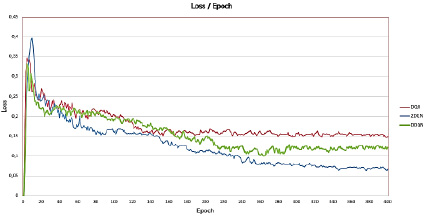
Рис. 2. График сравнения значений функции потерь для реализованных моделей
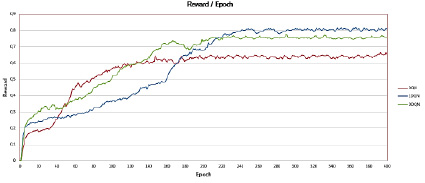
Рис. 3. График сравнения значения вознаграждения для реализованных моделей
Также стоит отметить, что значение, к которому сходится значение функции потерь для 2DQN, равно примерно 0,07, что говорит о хорошей эффективности модели. Другие модели: DQN и DDQN имеют немного большие средние значения функции потерь, при этом у модели DDQN заметна худшая сходимость из всех моделей. Далее рассмотрим график зависимости среднего значения вознаграждения к количеству пройденных эпох (рис. 3).
Из рис. 3 видно, что значение вознаграждения улучшается по мере увеличения количества пройденных тренировок, что также говорит, что модели действительно обучаются. На графике можно увидеть, что модели 2DQN и DDQN имеют лучшие значения вознаграждения Q, что говорит о превосходстве этих моделей, так как цель нейронной сети – максимизировать Q-значение. При этом график зависимости для DDQN метода имеет более аномальное поведение, чем модель 2DQN, так как график DDQN имеет скачкообразный рост, в то время как у модели 2DQN рост значения вознаграждения имеет более последовательное поведение. Также можно отметить, что у стандартной модели DQN значение вознаграждения достигает своего максимума за первые 100 эпох, при этом вознаграждение Q остается почти неизменным на протяжении всего обучения. Это показывает недостаток такого подхода: завышение оценок из-за недостаточно гибкой аппроксимации целевой функции. Как результат, производительность алгоритма глубокой Q-сети ухудшается при неравномерной оценке. У модели 2DQN рост значения вознаграждения идет поступательно, что можно связать с более взвешенным алгоритмом вычисления Q-значения.
Заключение
В работе были исследованы возможности использования методов глубокого обучения в сетях Vehicle-to-Everything для оптимизации трафика. Были рассмотрены три модели DQN сети: модель стандартного Q-обучения, модель Double DQN и модель Dueling DQN. Особенность архитектур двойной и дуэльной моделей заключается в том, что они иначе определяют ценность политики в сети DQN, создавая более стабильную нейронную сеть.
В результате лучшие показатели выдала модель двойного Q-обучения, которая модифицирует стандартную DQN модель путем более гибкой аппроксимации целевой функции. Также модель дуэльной DQN превосходит стандартную DQN модель, но по показателям функции потерь уступает двойной модели глубокого Q-обучения. При рассмотрении параметра среднего значения вознаграждения в течение обучения каждой модели можно заметить, что стандартная DQN модель изначально завышает вознаграждение по сравнению с другими моделями, при этом за время обучения значение вознаграждения незначительно увеличивается. Такое поведение стандартного алгоритма показывает, что чрезмерное завышение оценки вознаграждения отрицательно сказывается на эффективности нейронной сети. Другие две модели имеют более понятное поведение значения Q, что говорит о том, что они лучше обучаются и действительно могут использоваться для решения поставленной задачи. По результатам работы можно сделать вывод, что для оптимизации трафика в сетях Vehicle-to-Everything можно использовать методы глубокого Q-обучения. При этом стоит учитывать проблему стандартного DQN алгоритма и рассматривать его модификации для получения более эффективной нейронной сети. Для задачи распределения ресурсов в сетях V2X рекомендуется использовать метод двойного Q-обучения, так как он имеет более гибкую аппроксимацию целевой функции.
Библиографическая ссылка
Антропов Д.В., Осипов Н.А., Зудилова Т.В., Ананченко И.В., Осетрова И.С. ИССЛЕДОВАНИЕ МОДЕЛЕЙ ГЛУБОКОГО ОБУЧЕНИЯ ДЛЯ ОПТИМИЗАЦИИ ТРАФИКА В СЕТЯХ VEHICLE-TO-EVERYTHING // Современные наукоемкие технологии. 2022. № 8. С. 9-15;URL: https://top-technologies.ru/ru/article/view?id=39261 (дата обращения: 17.02.2026).
DOI: https://doi.org/10.17513/snt.39261



