Область применения систем массового обслуживания (СМО) очень широка: производство, сфера услуг, компьютерные сети, телекоммуникационные системы. К СМО можно отнести любые системы, в которых предполагается многократное выполнение однотипных операций, случайных по длительности и времени начала [1]. Наряду с телекоммуникационными системами одним из самых распространенных примеров СМО является торговая сеть. Здесь в роли заявок на обслуживание могут выступать сами товары, тогда под обслуживанием заявки понимается покупка товара. Обычно товар для реализации приходит партиями, в этом случае речь идет о групповом потоке заявок. Если же товар имеет ограниченный срок годности, то система его продажи относится к типу «СМО с ограниченным временем жизни заявки» [2, 3].
В классической теории систем массового обслуживания основными показателями эффективности их функционирования являются время пребывания и ожидания заявок, число заявок в системе, вероятность отказа (потери заявки). Эти характеристики относят к качеству обслуживания [4, 5]. Кроме показателей качества обслуживания существуют характеристики эффективности функционирования СМО, которые можно отнести к группе показателей, отражающих экономические особенности системы [6].
Целью нашего исследования является администрирование группового входного потока заявок, имеющих ограниченное время жизни. Характеристикой эффективности функционирования системы выбран один из ее экономических показателей – выручка от продажи товара.
Постановка задачи
Итак, рассмотрим процесс продажи партии товара, которая поступает в торговую точку одномоментно и имеет ограниченный срок годности. В общем случае и объем партии, и момент поступления товара, и средняя скорость его реализации являются величинами случайными. В этой работе рассмотрен вырожденный случай, параметры которого будут описаны ниже.
Положим, что при определенной отпускной цене товара торговая точка может его реализовать с определенной скоростью. Она может быть как постоянной величиной, так и функционально зависеть от времени или иметь случайный характер. Допустим, что скорость продажи товара не позволяет реализовать весь пришедший объем. Поскольку существует зависимость между скоростью продажи товара и его ценой, то очевидным является предположение, что, снизив отпускную цену товара в некоторый момент времени, можно обеспечить рост спроса на этот товар. Задача состоит в том, чтобы найти моменты времени снижения цены и величину этого снижения, которые обеспечат большую выручку по сравнению с первоначальным планом продаж.
Для построения аналитической модели задачи введем необходимые обозначения.
Q – объем партии товара;
Р1 – первоначальная отпускная цена;
Р2 – цена после точки принятия решения;
v1 – первоначальная скорость продаж;
v2 – скорость продаж после снижения цены;
tend – срок годности товара;
t* – момент времени снижения цены;
R1 – выручка при первоначальном плане продаж (базовая выручка);
R2 – суммарная выручка при изменении цены в момент t*.
В принятых обозначениях выручка при первоначальном плане продаж может быть получена по формуле
R1 = Р1Q1, (1)
где
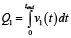 – (2)
– (2)
это количество товара, проданного с нулевого момента времени до истечения срока годности со скоростью продажи v1(t). Графическая иллюстрация представлена на рис. 1.
Интенсифицируем продажи в момент времени t*, снизив отпускную цену товара. Таким образом, общая выручка будет состоять из двух частей. Первая часть – выручка, полученная при продаже товара с первоначальной скоростью по первоначальной цене до момента t*. Вторая часть – выручка, полученная при продаже товара с повышенной скоростью по пониженной цене с момента t* до окончания срока годности:
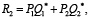 (3)
(3)
где
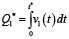 – (4)
– (4)
количество товара, проданного с нулевого момента времени до момента t* со скоростью продажи v1(t),
 – (5)
– (5)
количество товара, проданного с момента t* до окончания срока годности со скоростью продажи v2(t). Графическая иллюстрация представлена на рис. 2.
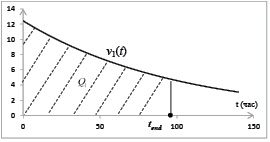
Рис. 1. Объем проданного товара
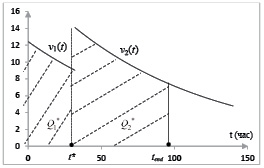
Рис. 2. Объем проданного товара с измененной ценой
Задача заключается в нахождении t*, P2, v2, таких, что
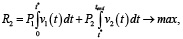 (6)
(6)
при условии
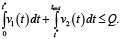
Имитационная модель
Задача (6) является некорректной, поэтому был выбран имитационный способ решения. Очевидными входными параметрами построенной имитационной модели являются объем партии товара Q, срок годности товара tend, первоначальная цена реализации Р1, первоначальная скорость продажи v1(t). И не совсем очевидным, но совершенно закономерным – зависимость между скоростью продажи и ценой v2(P1/P2).
В процессе имитации протестировано несколько функций v1(t): постоянная, линейная, экспоненциальная и квадратичная. Первой была рассмотрена постоянная скорость продажи. Коэффициенты других функций скорости подобраны так, чтобы значения базовой выручки были близки к варианту с постоянной скоростью.
На выходе мы получили набор векторов с компонентами: момент снижения цены – t*, величина снижения цены ∆P = P1 – P2, выручка – R2.
Для процесса имитации были заданы следующие входные данные: Q = 1000 ед., tend = 8 дней, P1 = 100 д. ед., v1(t) = 8 ед./час. При 12-часовом рабочем дне за 8 дней торговая точка продаст 768 единиц продукции из 1000 возможных и получит базовую выручку 76800 д. ед.
Остальные функции скорости выбраны так, чтобы базовая выручка была близка к 76800 и значение функции скорости в нулевой момент времени было бы теоретически приемлемым. Для линейной скорости продажи v1(t) = –0,06t + 10,9 базовая выручка составит R1 = 76992, начальная скорость v1(0) = 10,9. Для экспоненциальной v1(t) = e2,52 – 0,01t: R1 = 76697,75; v1(0) = 12,43. Для квадратичной v1(t) = –0,00025t2 + 8,768: R1 = 76829,49; v1(0) = 8,768.
При определении зависимости между ценой товара и интенсивностью продажи мы исходили из практических соображений. Были рассмотрены следующие зависимости:
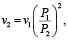 (7)
(7)
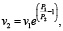 (8)
(8)
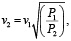 (9)
(9)
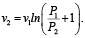 (10)
(10)
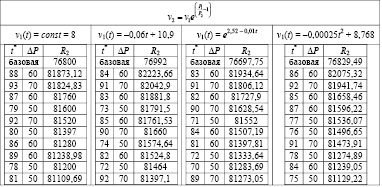
Десять лучших результатов в порядке убывания выручки для зависимости (7) представлены в табл. 1.
Результаты показывают, что для каждой функции скорости существует лучшее время для снижения цены – точка принятия решения. Заметим, что в малой окрестности этой точки расхождение в выручке составляет не более 0,5 %, и величина снижения цены одинакова – 20 д. ед.
Таблица 1
Лучшие значения выручки для зависимости (7)
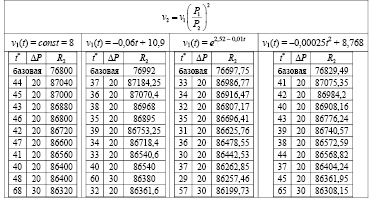
Таблица 2
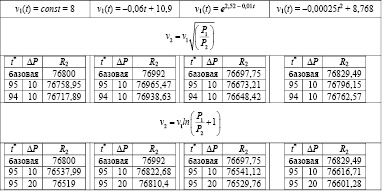
Лучшие значения выручки для зависимости (8)
Десять лучших результатов в порядке убывания выручки для зависимости (8) представлены в табл. 2.
Для зависимости (8) тоже нашлись единственные точки принятия решения. Значения самых лучших вариантов выручки еще ближе к максимальному. Но об окрестности точки принятия решения и однозначности величины скидки на товар говорить не приходится.
Для зависимостей (9) и (10) все совсем иначе – не существует такого момента времени, изменение цены в который даст прирост выручки относительно базовой. Лучшие результаты наглядно приведены в табл. 3.
Таким образом, если рассматривать функцию изменения скорости продаж v2 как зависимость от отношения цен P1 / P2, то можно говорить о выпуклости функции v2 как о необходимом условии существования точки принятия решения, позволяющей увеличить базовую выручку.
Таблица 3
Лучшие значения выручки для зависимостей (9) и (10)
Заключение
Сформулирована задача нахождения момента времени для увеличения предполагаемой выручки при продаже партии товара с ограниченным сроком годности.
Построена имитационная модель для решения поставленной задачи. Проведен ряд экспериментов для разных функций скорости продажи, подобранных по величине предполагаемой выручки.
Сделан вывод о наличии точки принятия решения о снижении цены для определенных входных параметров и свойствах функций, определяющей зависимость скорости продажи от цены.
Библиографическая ссылка
Шайдуллина Н.К., Печеный Е.А., Нуриев Н.К. ПРОБЛЕМА ЭФФЕКТИВНОГО АДМИНИСТРИРОВАНИЯ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ЖИЗНИ ЗАЯВОК // Современные наукоемкие технологии. 2022. № 7. С. 69-73;URL: https://top-technologies.ru/ru/article/view?id=39235 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.39235



