Восстановление суставов после травмы или операции осуществляется постепенной разработкой, увеличением их подвижности и гибкости путем механотерапии. Механотерапевтические аппараты позволяют облегчить или обеспечить необходимые движения для увеличения подвижности в суставах, а также для тренировки определенных групп мышц. При отсутствии мышечной активности больного применяют аппараты пассивного действия (прикроватные или стационарные), которые сами задают движение сустава от внешнего источника [1]. К таким аппаратам относятся специальные тренажеры для локтевого (например, ARTROMOT E2, Kinetec 6080 elbow CPM) и коленного (например, Opti Flex 3 Knee CPM) суставов, оснащаемые электроприводами и контроллерами [2, 3], стоимостью до 500 тыс. руб. Если пациент использует механотерапевтический аппарат за счет своей собственной мышечной активности, то такие аппараты называются аппаратами активного действия, или тренажерами [4]. Такие аппараты предоставляют возможность больному в зависимости от характера и выраженности болевых ощущений задавать амплитуду движений. Они бывают, как правило, трех типов – основанные на принципе блока (использование веса груза или пружины), на принципе маятника (использование инерции) и изокинетические. Стоимость аппаратов активного действия невысокая, но они лишены регулировки величины создаваемой нагрузки в широком диапазоне. При многих патологических состояниях суставов в процессе механотерапии требуется полностью исключить или значительно уменьшить взаимодавление суставных поверхностей. Известные механотерапевтические аппараты активного действия не обеспечивают указанное требование. При работе с аппаратами механотерапии задействуется сравнительно небольшая мышечная группа, например только те мышцы, которые отвечают за сгибание или разгибание. Анализ устройства тренажеров активного действия для локтевого и коленного суставов показывает, что их общим техническим недостатком является отсутствие регулирования величины и направления нагрузки и наличие сил, возникающих в устройстве нагружения при работе и приводящих к взаимодавлению суставных поверхностей, что отрицательно воздействует на состояние травмированного сустава.
Целью работы является решение вопросов создания активного механотерапевтического устройства для тренажеров коленного и локтевого суставов, реализующего переменную по величине и направлению нагрузочного момента без образования сил взаимодавления суставных поверхностей.
Материалы и методы исследования
В качестве устройства моментного нагружения суставов с постоянными параметрами нагрузки без образования сил взаимодавления суставных поверхностей предлагается использовать механизм для статической моментной разгрузки, описанный в работе [5]. Механизм реализует статическую моментную разгрузку привода поворота звена в вертикальной плоскости без образования поперечных или продольных сил при фиксированном моменте нагрузки. Для реализации переменной величины нагрузки можно использовать механизм нагружения, схема которого приведена на рис. 1.
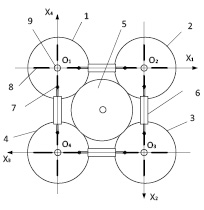
Рис. 1. Схема механизма нагружения: 1, 2, 3, 4 – внешние зубчатые колеса механизма (ЗК1); 5 – внутреннее зубчатое колесо механизма (ЗК2); 6 – упругие элементы; 7 – точки крепления упругих элементов на ЗК2; 8 – конструктивные элементы крепления упругих элементов на ЗК2; 9 – оси крепления зубчатых колес. Точками О1,О2,О3 и О4 обозначены геометрические центры осей крепления ЗК1
При повороте ЗК2 также повернутся ЗК1, причем углы поворота могут быть равными либо различными в зависимости от соотношения диаметров колес ЗК2 и ЗК1. При повороте колес упругие элементы, выполненные из латексной ленты, трубчатой резины или в виде пружин растяжения, будут растягиваться, создавая усилия и моменты нагружения 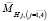 относительно центров колес ЗК1. Аксиальные составляющие зубчатых зацеплений ЗК2 и ЗК1создадут суммарный момент на внутреннем зубчатом колесе
относительно центров колес ЗК1. Аксиальные составляющие зубчатых зацеплений ЗК2 и ЗК1создадут суммарный момент на внутреннем зубчатом колесе 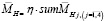 (η – кпд механизма). При этом, как будет показано ниже, этот момент может быть противодействующим МНП или сопутствующий МНС направлению движения тренируемого органа из начального положения. Отсутствие сил в механизме обеспечивается за счет взаимной компенсации противоположных относительно центра ЗК2 радиальных составляющих усилия зацепления.
(η – кпд механизма). При этом, как будет показано ниже, этот момент может быть противодействующим МНП или сопутствующий МНС направлению движения тренируемого органа из начального положения. Отсутствие сил в механизме обеспечивается за счет взаимной компенсации противоположных относительно центра ЗК2 радиальных составляющих усилия зацепления.
Расположим по осям двух смежных внешних зубчатых колес (СЗК1) оси 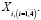 Тогда совокупность координат возможных точек крепления упругого элемента на одном из ЗК1 по оси Xi можно представить в виде множества
Тогда совокупность координат возможных точек крепления упругого элемента на одном из ЗК1 по оси Xi можно представить в виде множества
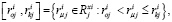 (1)
(1)
где 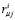 – координаты -й точки по оси Xi для j-го ЗК1,
– координаты -й точки по оси Xi для j-го ЗК1, 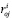 и
и 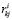 – координаты граничных точек,
– координаты граничных точек, 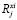 – совокупность вещественных чисел по оси Xi для j-го ЗК1. Из рис. 1 следует, что имеют место 4 варианта соединения каждой пары смежных ЗК1 в начальном положении. Например, для пары колес 1 и 2 на рис. 1 эти варианты можно описать выражениями
– совокупность вещественных чисел по оси Xi для j-го ЗК1. Из рис. 1 следует, что имеют место 4 варианта соединения каждой пары смежных ЗК1 в начальном положении. Например, для пары колес 1 и 2 на рис. 1 эти варианты можно описать выражениями
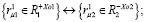 (2)
(2)
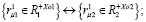 (3)
(3)
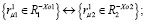 (4)
(4)
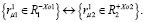 (5)
(5)
Здесь 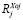 – положительные или отрицательные значения координат точек крепления упругих элементов на колесах 1 и 2 по оси Х1 относительно точек О1 и О2. В общем случае
– положительные или отрицательные значения координат точек крепления упругих элементов на колесах 1 и 2 по оси Х1 относительно точек О1 и О2. В общем случае 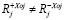 .
.
Рассмотрим условия формирования нагрузочного момента в механизме применительно к смежным колесам 1 и 2. На рис. 2 приведены расчетные схемы определения нагрузочного момента, возникающего на внутреннем колесе от действия колес 1 и 2, соединенным упругим элементом в точках Bj на расстояниях 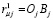 от центров поворота колес 1 и 2 по варианту (2) .
от центров поворота колес 1 и 2 по варианту (2) .
Примем, что радиусы колес 1 и 2 одинаковы и при повороте внутреннего колеса при работе тренажера из начального положения по часовой стрелке они поворачиваются на некоторый угол α. Вектор нагрузочного момента МН12 на внутреннем колесе от действия колес 1 и 2 равен векторной сумме:
МН12 = МН1 + МН2, (6)
где МН1, МН2 – составляющие нагрузочного момента от действия колес 1 и 2. Из рис. 2 следует, что скалярная величина момента МНj определяется из очевидного соотношения
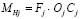 , (7)
, (7)
где Fj – модуль усилия, развиваемого упругим элементом (F1 = F2), OjCj – длина нормали к линии действия усилия Fj.
Обозначим O1O2 = H, воспользуемся теоремой синусов, а также формулами приведения для тригонометрических функций и из рассмотрения схемы, представленной на рис. 2, а для левого смежного колеса получим соотношения
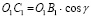 ;
;
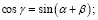
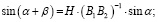
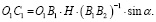 (8)
(8)
Тогда выражение (7) запишется в виде
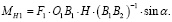 (9)
(9)
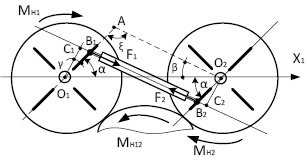
Рис. 2. Расчетная схема определения нагрузочного момента от действия зубчатых колес 1 и 2 (соединение колес упругим элементом по варианту (2))
Полагаем, что
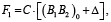 (10)
(10)
где C – коэффициент жесткости упругого элемента, (B1B2)0 и Δ – его начальная длина и величина деформации. Выполнение условия (10) обеспечивается соответствующим предварительным растяжением упругого элемента или созданием в элементе начального усилия без его деформации (например, межвиткового давления в пружине растяжения). Поскольку B1B2 = 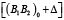 , то после соответствующих подстановок получим
, то после соответствующих подстановок получим
MH1 = O1B1 ∙ H ∙ C ∙ sinα. (11)
Так как O1B1, H и C – постоянные величины, то MH1 изменяется по гармоническому закону, аналогичному изменениям момента в локтевом, коленном и голеностопном суставах при перемещениях предплечья, голени и стопы в вертикальной плоскости.
Для правого смежного колеса выражение (11) примет вид
MH2 = O2B2 ∙ H ∙ C ∙ sinα, (12)
а величина суммарного нагрузочного момента от двух смежных колес равна
MH12 = (O1B1 + O2B2) ∙ H ∙ C ∙ sinα
или в общем виде
MH12 = 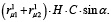 (13)
(13)
При равенстве 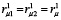 имеем
имеем
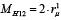
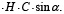 (14)
(14)
Так как соединение всех пар смежных ЗК1 упругими элементами должно выполняться по одному варианту и с одинаковыми величинами 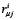 , то, используя выражение (14) для всего механизма, можно записать
, то, используя выражение (14) для всего механизма, можно записать
MH = 4 ∙ MH12 = 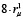 ∙ H ∙ C ∙ sinα. (15)
∙ H ∙ C ∙ sinα. (15)
Тогда, например, при 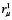 = 15 мм; Н = 84 мм и С = 1 Н/мм максимальное значение нагрузочного момента равно MHмакс = 10,8 Н∙м.
= 15 мм; Н = 84 мм и С = 1 Н/мм максимальное значение нагрузочного момента равно MHмакс = 10,8 Н∙м.
В общем случае 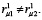 Обозначим разницу
Обозначим разницу 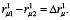 Тогда из рис. 2 несложно получить выражение для величины уменьшения момента MH12 вследствие обозначенной выше разницы:
Тогда из рис. 2 несложно получить выражение для величины уменьшения момента MH12 вследствие обозначенной выше разницы:
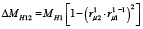 . (16)
. (16)
В безразмерном виде выражение (16) можно записать следующим образом:
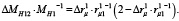 (17)
(17)
Производная 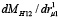 равна:
равна:
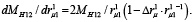
На рис. 3 приведена графическая зависимость выражения (17).
Из рис. 3 следует, что указанная выше зависимость имеет квадратичный характер.
По аналогии с приведенным выше расчетом схемы (2) для схемы (3) можно получить
MH12 = (O1B1 – O2B2) ∙ H ∙ C ∙ sinα
или в общем виде
MH12 = 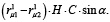 (18)
(18)
Из выражений (13) и (18) следует, что в пределах угла поворота 0 < α ≤ π/2 знак нагрузочного момента не изменяется.
При соединении колес по схеме (2) момент максимален, а при соединении по варианту (3) нагрузочный момент может стать сопутствующим MС12 при 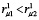 и равным нулю при
и равным нулю при 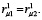
Поскольку вариант крепления упругих элементов (5) аналогичен варианту (2), то можно записать
MH12 = 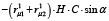 = MHС12 (19)
= MHС12 (19)
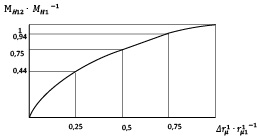
Рис. 3. Графическая зависимость ΔMH12 ∙ MH1–1 от соотношения 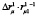
Результаты исследования и их обсуждение
На рис. 4 приведены графики моментов нагрузки, создаваемых механизмом в зависимости от угла поворота ЗК1 в диапазоне 0 < α ≤ π/2.
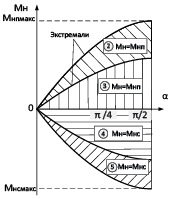
Рис. 4. Графики моментов нагрузки, создаваемых механизмом в зависимости от угла поворота ЗК1
Цифры соответствуют вариантам (2)–(5) соединения колес ЗК1 упругими элементами, приведенным выше.
В верхней полуплоскости моменты нагрузки противодействующие, а в нижней – сопутствующие движению.
Исходя из практических соображений нет необходимости в большом количестве точек крепления упругих элементов. Рассмотрим работу механизма на примере двух смежных колес 1 и 2, ограничившись шестью точками крепления (по три с каждой стороны от центра вдоль оси X1) для каждого колеса ЗК1. Полагая, что матрица смежности представляет собой матрицу размером 6×6, состоящую из единиц, запишем матрицу знаков моментов, создаваемых упругим элементом на каждом колесе при различных вариантах расположения точек их крепления при условии 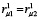 (формула (20)).
(формула (20)).
Нулевые значения на главной диагонали матрицы (20) указывают на отсутствие момента нагрузки. Знаком «+» отмечены противодействующие нагрузочные моменты, а знаком «–» – сопутствующие. Из матрицы (20) следует, что при использовании всего 6 точек крепления упругого элемента на колесе мы получим 30 различных зависимостей и максимальных значений нагрузочного момента: 15 противодействующих и 15 сопутствующих. При использовании 8 точек можно получить 76 различных зависимостей и значений нагрузочного момента без замены упругих и других конструктивных элементов механизма, что может быть достаточным для тренировки мышц различных суставов людей разных возрастных групп. На рис. 5 приведены схемы крепления механизма при тренировке локтевого и коленного суставов.
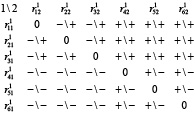 (20)
(20)

Рис. 5. Схемы крепления механизма при тренировке локтевого и коленного суставов
Следует отметить, что предложенное и описанное простое устройство с изменяемой нагрузкой может быть использовано не только в процессе восстановления мышц после травм или операций на суставах, но и для тренировки мышц бедра и предплечья здоровых людей.
Заключение
Предложено достаточно простое механическое устройство активного механотерапевтического аппарата для тренажеров коленного и локтевого суставов, реализующего переменный и регулируемый по величине и направлению нагрузочный гармонический момент без образования сил взаимодавления суставных поверхностей.
Библиографическая ссылка
Умнов В.П. МОМЕНТНЫЙ МЕХАНИЗМ С ИЗМЕНЯЕМОЙ ВЕЛИЧИНОЙ И НАПРАВЛЕНИЕМ НАГРУЗКИ ДЛЯ МЕХАНОТЕРАПИИ СУСТАВОВ // Современные наукоемкие технологии. 2022. № 5-2. С. 255-260;URL: https://top-technologies.ru/ru/article/view?id=39180 (дата обращения: 14.03.2026).
DOI: https://doi.org/10.17513/snt.39180



