И.П. Павлов отмечал, что «животный организм представляет крайне сложную систему, состоящую из почти бесконечного ряда частей, связанных как друг с другом, так и в виде единого комплекса с окружающей природой и находящихся с ней в равновесии» [1, с. 106]. Комплексная оценка здоровья одновременно по нескольким факторам риска является одной из актуальных и недостаточно изученных проблем в медицине. Часто применяемые в таких случаях экспертные оценки нельзя считать в полной мере объективными [2].
Одним из направлений для комплексного оценивания здоровья может быть использование энтропии, являющейся одной из наиболее универсальных характеристик сложных систем [3, 4]. Такие системы обычно обладают неопределенным (стохастическим) характером поведения и состоят из множества сложным образом взаимосвязанных между собой элементов. При этом все компоненты связаны между собой некоторым образом. Важно указать на то, что имеет место неоднозначность выбора элементов в сложной системе [5, 6]. В этой ситуации ее часто представляют в виде случайного вектора (с.в.) Y = (Y1, Y2, ... , Ym), в котором каждая компонента Yi является одномерной случайной величиной, характеризующей функционирование соответствующего элемента системы [7].
Представляет интерес вопрос использования энтропии для мониторинга систем. В [8] предложено использование энтропийного анализа для мониторинга популяционного здоровья. В его основе векторное представление дифференциальной энтропии (далее – энтропии). Использование системно-энтропийного анализа позволило понять основные системные причины ухудшения популяционного здоровья, а для формирования рекомендаций по улучшению здоровья также необходима количественная оценка вклада в его ухудшение каждого из факторов риска [9]. Отметим, что энтропийно-вероятностный (ЭВ) подход, объединяющий системно-энтропийный и риск-анализ, предложен и апробирован для исследования популяций [10]. Поэтому представляет интерес рассмотреть возможности ЭВ моделирования для мониторинга индивидуального состояния здоровья.
Цель исследования – разработать методику энтропийно-вероятностного мониторинга индивидуального состояния здоровья на примере сердечно-сосудистой системы.
Материалы и методы исследования
Имеем два множества (случайных вектора): X = (X1, X2, X3) – множество входных показателей, Y = (Y1, Y2, Y3) – множество факторов риска (выходных показателей) (см. табл. 1). Выбор выходных показателей объясняется следующими причинами. Во-первых, они являются обобщенными показателями как состояния человеческого здоровья и качества работы сердечно-сосудистой системы в частности [11, 12]. Во-вторых, эти показатели доступны для измерения. В-третьих, ставилась цель показать возможности предлагаемой методики в целом. Для более глубокого исследования состояния здоровья понадобится большее число наблюдаемых показателей и наблюдение в медицинском учреждении, что в настоящее время осложнено из-за ковидных ограничений. Выбор входных показателей X обусловлен наличием метеозависимости, проявляющейся в избыточном реагировании человека на изменения условий окружающей среды [13].
Таблица 1
Анализируемые показатели
|
Обозначение |
Показатель |
|
X1 |
Атмосферное давление, мм рт. ст. |
|
X2 |
Влажность воздуха, % |
|
X3 |
Суточное время, % от 24 ч |
|
Y1 |
Систолическое артериальное давление (САД), мм рт. ст. |
|
Y2 |
Диастолическое артериальное давление (ДАД), мм рт. ст. |
|
Y3 |
Частота сердечных сокращений (ЧСС), уд/мин |
Системно-энтропийный анализ включает в себя следующее. Общая энтропия непрерывного с.в.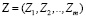 
определяется по формуле [8]
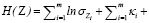
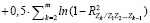, (1)
где
,
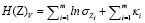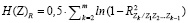– энтропия хаотичности (энтропия с.в. с взаимно независимыми компонентами) и энтропия самоорганизации (показывает взаимодействие между подсистемами – чем меньше коэффициент, тем больше корреляционная взаимосвязь между компонентами системы, тем меньше общая энтропия; при наличии функциональной связи между хотя бы двумя компонентами H(Z)R = –∞, при взаимной независимости всех компонент H(Z)R = 0)
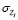– стандартное отклонение; 
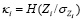– энтропийный показатель типа закона распределения случайной величины Zi; 
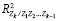– индексы детерминации регрессионных зависимостей. Разделим энтропию хаотичности на две составляющие
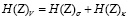, (2)
где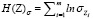 
– «хаотичности энтропия рассеяния» (характеризует вклад в энтропию хаотичности степени рассеяния всех элементов системы Z), 
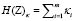– «хаотичности энтропия распределения» (определяет вклад в энтропию хаотичности форм распределения компонент многомерной с.в. Z), H(Y)comp = H(Y)R + H(Y)σ – «энтропия сравнения» (если H(Y)κ неизменна, то H(Y)comp облегчает восприятие изменения энтропии).
Анализ распределений компонент случайных векторов X и Y подтвердил вывод [7] о близости распределений к нормальному закону. Поэтому вместо (1) и (2) имеем
,
,
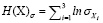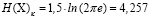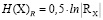, (3)
,
,
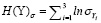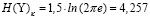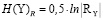. (4)
Отметим, что между энтропией самоорганизации и теснотой корреляционной связи между компонентами с.в. X и Y существует взаимно однозначная функциональная связь.
Энтропия взаимосвязи H(X ∩ Y) между векторами X и Y позволит количественно оценивать влияние метеорологических факторов на состояние сердечно-сосудистой системы. Она изменяется от 0 (соответствует независимости между X и Y) до +∞ (в случае, когда хотя бы один из показателей Yj функционально связан с хотя бы одним показателем Xi). Для гауссовых случайных векторов [10]
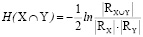. (5)
Вероятность неблагоприятного исхода P(D) (вероятность перехода испытуемого в «риск-зону» по факторам риска Y1, Y2, Y3 относительно пороговых уровней) как [9]
,
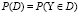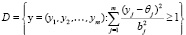. (6)
Абсолютное и относительное изменение риска за счет добавления фактора Yk равно
,
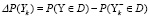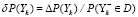, (7)
где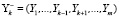 
.
Результаты исследования и их обсуждение
В качестве исходных данных использовались ежедневные показания двух человек (испытуемый 1 – мужчина 47 лет; испытуемый 2 – мужчина 60 лет), давших согласие на участие в экспериментах. Поскольку мы рассматриваем не популяционный, а индивидуальный мониторинг, то число испытуемых несущественно (у каждого испытуемого могут быть свои индивидуальные особенности в зависимости от возраста и т.п., а значит, и разные исследуемые показатели). С учетом того, что ставилась задача описания методики в целом, такого числа испытуемых достаточно. Измерения артериального давления и пульса проводили в соответствии с клиническими рекомендациями [14] с помощью тонометра Sanitas SBC 23: погрешность измерения давления ±3 мм рт. ст.; погрешность измерения пульса ±5 %. Погодные условия фиксировались с сайта https://www.gismeteo.ru/. Результаты наблюдений и состояние здоровья испытуемых контролировались квалифицированным врачом-терапевтом. Количество наблюдений для испытуемых составило 87 и 285 измерений (в среднем более 50 измерений в месяц), достаточно для имеющейся погрешности тонометра. Анализ проводился с помощью программы [15].
ЭВ мониторинг показателей сердечно-сосудистой системы для испытуемого 1.
В табл. 2 представлены средние уровни САД, ДАД, ЧСС, энтропийные коэффициенты, показатели риск-анализа в различное время дня (утро, день, вечер) и в период до и после 21.02.22. Проведение анализа до и после 21.02.22 обусловлено тем, что по данным анамнеза после 21.02.22 произошло существенное изменение в состоянии здоровья испытуемого 1 вследствие стресса. У испытуемого 1 не было медицинских оснований учитывать влияние на сердечно-сосудистую систему климатических условий, поэтому энтропийный анализ взаимосвязи между входными показателями X и факторами риска Y не проводился.
Таблица 2
Результаты ЭВ мониторинга показателей сердечно-сосудистой системы испытуемого 1 в различные временные периоды
|
Показатель |
31.01 – 20.03.22 |
31.01 – 21.02.22 |
22.02 – 20.03.22 |
Утро |
День |
Вечер |
|
n |
84 |
47 |
37 |
39 |
21 |
24 |
|
Y1 M±m (σ) |
157,0±1,4* (8,52) |
|||||
|
Y2 M±m (σ) |
96,6±1,32** (8,04) |
90,7±1,48* (6,78) |
92,0±1,43^^ (6,99) |
|||
|
Y3 M±m (σ) |
||||||
|
H(Y)R |
-0,35 |
-0,23 |
-0,44 |
-0,31 |
-0,63 |
-0,45 |
|
H(Y)σ |
6,04 |
5,30 |
6,37 |
5,896 |
5,88 |
5,88 |
|
H(Y)κ |
4,26 |
4,26 |
4,26 |
4,26 |
4,26 |
4,26 |
|
H(Y)v |
10,30 |
9,56 |
10,62 |
10,15 |
10,13 |
10,13 |
|
H(Y) |
9,95 |
9,32 |
10,18 |
9,85 |
9,5 |
9,68 |
|
H(Y)comp |
5,7 |
5,07 |
5,92 |
5,59 |
5,24 |
5,425 |
|
P(D) |
0,397 |
0,171 |
0,631* |
0,503 |
0,275 |
0,305 |
|
δP(Y1), % |
24,5 |
25,0 |
20,2 |
13,2 |
48,7 |
58,1 |
|
δP(Y2), % |
22,05 |
23,5 |
13,9 |
37,7 |
6,8 |
11,5 |
|
δP(Y3), % |
68,4 |
136,0 |
55,6 |
62,5 |
82,4 |
49,7 |
Примечание. M – средняя (арифметическая) величина; m – средняя ошибка средней величины; σ –стандартное отклонение; n – количество значений САД, ДАД, ЧСС; ** – p < 0,01 при сравнении представленной группы с предыдущей по временному периоду (анализ проводился для САД, ДАД, ЧСС, P (D)); * – p < 0,001; ^^ – p < 0,01 при сравнении между группами «Утро» / «Вечер» для САД, ДАД, ЧСС; n – количество измерений
Уровни для риск-анализа определим так: оптимальный – среднее арифметическое из всех измерений, пороговые уровни (верхний/нижний) – ±σ (σ – стандартное отклонение), критические уровни (верхний/нижний) – ±2σ. Использование уровней для риск-анализа на основании клинических рекомендаций (например, оптимальный уровень артериального давления 120/80 мм рт. ст., верхние пороговые и критические уровни, соответствующие 1 и 3 степеням артериальной гипертензии и т.д.) в данном случае неудобно, так как из-за высоких значений артериального давления у испытуемого вероятность P(D), например, за весь период будет равна 0,998, что затрудняет проведение анализа.
Анализ по средним величинам показывает, что утром выше средний уровень ДАД в сравнении с дневным (на 7,2 %) и вечерним (на 5,6 %) временем при неизменных САД и ЧСС. При этом риск-анализ фиксирует существенное снижение P(D) с 50,3 % до 27,5 %. Изменение энтропии аналогично – H(Y)comp уменьшилась с 5,59 до 5,24 при существенном снижении энтропии самоорганизации (с –0,31 до –0,63), что свидетельствует об усилении внутренних взаимосвязей и стабилизации функционирования сердечно-сосудистой системы в дневное время. Более существенное изменение показателей риск-анализа в сравнении с анализом по отдельным подсистемам позволяет выявить более «тонкие» изменения, особенно при недостатке данных (малом числе наблюдений).
После 21.02.22 достоверно увеличились уровни САД (на 4,7 %), ДАД (на 4,9 %). При этом H(Y)comp возросла с 5,07 до 5,92 (на 16,7 %) с уменьшением H(Y)R с –0,23 до –0,44 (стабилизация на более «негативном» уровне). Риск возрос еще больше: P(D) увеличилась с 17,1 % до 63,1 % (p < 0,001). Дату 21.02.22, после которой произошло существенное ухудшение показателей сердечно-сосудистой системы, мы знали из данных анамнеза.
Применим далее ЭВ мониторинг для периодов с равным количеством измерений (n = 30) и «перекрытием» смежных групп, т.е. группы с номерами измерений 1–30, 16–45, 31–60, 46–75, 61–84. Результаты представлены в табл. 3.
Таблица 3
Результаты ЭВ мониторинга показателей сердечно-сосудистой системы испытуемого 1 для периодов с равным количеством измерений
|
Показатель |
Период 1 |
Период 2 |
Период 3 |
Период 4 |
Период 5 |
|
Интервал |
31.01–13.02.22 |
08.02–20.02.22 |
14.02–02.03.22 |
21.02–15.03.22 |
03.03–20.03.22 |
|
n |
1–30 |
16–45 |
31–60 |
46–75 |
61–84 |
|
Y1 M±m (σ) |
148,25±1,29 (7,05) |
150,4±1,33 (7,3) |
152,5±1,31 (7,16) |
155,5±1,59 (8,72) |
159,9±1,3*** (6,37) |
|
Y2 M±m (σ) |
91,1±1,04 (5,68) |
91,75±0,79 (4,35) |
94,05±1,22 (6,71) |
96,1±1,59 (8,73) |
97,9±1,44 (7,08) |
|
Y3 M±m (σ) |
71,9±1,23 (6,74) |
72,0±1,15 (6,28) |
74,3±1,35 (7,39) |
74,75±1,6 (8,78) |
71,5±1,69 (8,28) |
|
H(Y)R |
-0,28 |
-0,21 |
-0,23 |
-0,5 |
-0,58 |
|
H(Y)σ |
5,55 |
5,24 |
5,82 |
6,45 |
5,86 |
|
H(Y)κ |
4,26 |
4,26 |
4,26 |
4,26 |
4,26 |
|
H(Y)v |
9,8 |
9,5 |
10,08 |
10,71 |
10,12 |
|
H(Y) |
9,52 |
9,29 |
9,85 |
10,21 |
9,54 |
|
H(Y)comp |
5,27 |
5,04 |
5,59 |
5,95 |
5,28 |
|
P(D) |
0,204 |
0,198 |
0,395 |
0,61 |
0,599 |
Примечание. M – средняя (арифметическая) величина; m – средняя ошибка средней величины; σ –стандартное отклонение; n – номера измерений САД, ДАД, ЧСС; *** – p < 0,05 при сравнении представленной группы с предыдущей (анализ проводился для САД, ДАД, ЧСС).
При однофакторном анализе (по одному показателю в отдельности) обнаружено только достоверное увеличение САД на 2,8 % в группе № 5 относительно периода № 4. Определить момент, когда произошло резкое изменение в системе при анализе по одному показателю в отдельности не представляется возможным. При динамическом энтропийно-вероятностном анализе в периоде 3 зафиксирован рост H(Y)comp на 10,9 % с 5,04 до 5,59. Показатели риск-анализа фиксируют еще более выраженные изменения при переходе из периода № 2 в № 3 – рост P(D) с 19,8 % до 39,5 %. Уменьшение H(Y)R с –0,23 в периоде № 3 до –0,5 в периоде № 4 при одновременном росте остальных энтропийных коэффициентов и риска P(D) показывает стабилизацию системы на более «негативном» уровне. Таким образом, метод ЭВ мониторинга в отличие от однофакторного анализа позволяет выявить момент, когда в системе произошел качественный сдвиг (резкое ухудшение) – это середина интервала 14.02–02.03.22, что совпадает, в том числе с данными анамнеза (22.02.2022) (табл. 2).
ЭВ мониторинг показателей сердечно-сосудистой системы для испытуемого 2.
У испытуемого 2 были основания учитывать влияние климатических условий на факторы риска. Поэтому показатели Xi фиксировались и проводился энтропийный анализ взаимосвязи между входными показателями X и факторами риска Y. Ввиду ограниченности объема статьи не будем приводить таблицы, аналогичные табл. 2, 3, а представим результаты мониторинга состояния его здоровья в графическом виде (рис. 1–3). Весь диапазон был разбит на 8 интервалов: k = 1 (01.11.21 – 20.11.21), k = 2 (21.11.21 – 10.12.21), k = 3 (11.12.21 – 31.12.21), k = 4 (01.01.22 – 20.01.22), k = 5 (21.01.22 – 10.02.22), k = 6 (11.02.22 – 28.02.22), k = 7 (01.03.22 – 20.03.22), k = 8 (21.03.22 – 10.04.22). Следует отметить, что испытуемому 2 в начале февраля была сделана операция, не связанная с сердечно-сосудистой системой.
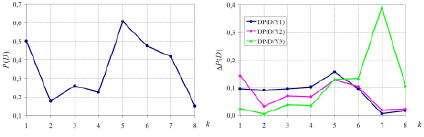
Из рис. 1, а, видно, что энтропии хаотичности, как входных показателей, так и факторов риска, ведут себя достаточно стабильно. Энтропия самоорганизации (рис. 1, б) входных показателей близка к нулю (соответствует их независимости), однако в начале года было некоторое уменьшение, вызванное случайным появлением корреляции между влажностью воздуха и суточным временем фиксации данных (эту корреляцию можно считать нонсенс-корреляцией, обусловленной фактором случайности). Энтропия самоорганизации вначале растет до конца января, а затем начинает стабильно уменьшаться (все три фактора риска становятся взаимно более коррелированными), что может быть охарактеризовано как их более согласованное поведение. А одновременное снижение риска (рис. 2, а) позволяет говорить об улучшении функционирования сердечно-сосудистой системы. Влияние САД и ДАД на вероятность P(D) с февраля стало стабильно уменьшаться (рис. 2, б). Скачок роста ΔP(Y3) из-за ЧСС вызван увеличением физической нагрузки и к концу анализируемого периода он существенно уменьшился.
Как видно из рис. 3, энтропия взаимосвязи между атмосферным давлением, влажностью воздуха и суточным временем и факторами риска в декабре – январе увеличилась, а с середины февраля стала монотонно уменьшаться (факторы риска в меньшей степени стали зависеть от климатических условий), что также можно характеризовать как улучшение работы сердечно-сосудистой системы.
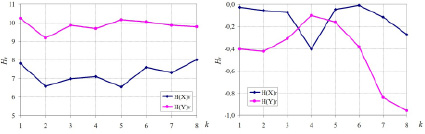
а) б)
Рис. 1. Значения энтропий для множеств показателей X и Y: а) энтропии хаотичности H(X)V и H(Y)V; б) энтропии самоорганизации H(X)R и H(Y)R
а) б)
Рис. 2. Риск-анализ сердечно-сосудистой системы по показателям Y: а) значения риска P(D); б) абсолютные изменения риска ΔP(Yk) за счет каждого из факторов риска Yk
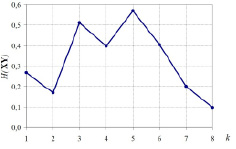
Рис. 3. Значения энтропии взаимосвязи H(X ∩ Y)
Заключение
1. Индивидуальный энтропийно-вероятностный мониторинг позволяет обнаружить момент существенного изменения функционирования сердечно-сосудистой системы и определить, какие из множества факторов на это повлияли (через анализ энтропии взаимосвязи). Полагаем, что индивидуальный энтропийно-вероятностный мониторинг обладает универсальностью и может использоваться в других областях клинической медицины, особенно в тех, где постоянно с использованием информационных технологий фиксируется большое количество параметров функционирования разных систем, например в функциональной диагностике, в реанимационной практике и др.
2. Наряду с риск-анализом и системно-энтропийным анализом имеется возможность совместного анализа различных исследуемых показателей с множеством входных показателей, оказывающих влияние на состояние здоровья конкретного человека.
3. Методика апробирована на примере сердечно-сосудистой системы. Результаты энтропийно-вероятностного мониторинга согласуются с данными о фактическом состоянии здоровья испытуемых.
Работа выполнена при поддержке РФФИ (грант № 20-51-00001).
Библиографическая ссылка
Тырсин А.Н., Яшин Д.А. ИНДИВИДУАЛЬНЫЙ ЭНТРОПИЙНО-ВЕРОЯТНОСТНЫЙ МОНИТОРИНГ ФУНКЦИОНИРОВАНИЯ СЕРДЕЧНО-СОСУДИСТОЙ СИСТЕМЫ // Современные наукоемкие технологии. – 2022. – № 5-2. – С. 219-225;URL: https://top-technologies.ru/ru/article/view?id=39174 (дата обращения: 15.01.2025).