Создание общего аппарата анализа, оценивания состояния и управления сложных технических систем, под которыми будем понимать некоторую структуру функционально взаимодействующих подсистем даже с известной (нелинейной, вообще говоря) математической моделью их функционирования, вряд ли возможно: «…не верю, что можно найти общие закономерности в поведении сложных систем» (Джон фон Нейман).
Система анаэробной биологической очистки (САБО) [1] как объект моделирования [2, 3], анализа [4] и конструирования системы управления [5] обладает всеми признаками сложного объекта [6] (по Л.А. Растригину), поведение которого существенно усложняется наличием динамики биомассы с математическим описанием в виде уравнений динамики «хищник – жертва»: 1) отсутствие полного математического описания; 2) «зашумленность» объекта (системы), реализуемая неожиданностью поведения объекта для исследователя; 3) «сопротивляемость» к управлению; 4) нестационарность системы (дрейф характеристик во времени); 5) неоднородность (неповторяемость) результатов экспериментов и слабая доступность к их проведению; 6) многомерность, многосвязность основных характеристик; 7) нелинейность многомерного описания.
Цель настоящего исследования – изложение двух подходов к стабилизации желаемых состояний систем анаэробной биологической очистки сточных вод (САБО): аналитического на основе концепции самоорганизации [6, 7] и имитационного, и их численное сравнение на предмет робастности в условиях неизвестных возмущений.
1.1. Математическая модель САБО как объекта управления
Согласно базовой модели ADM-1 [1] для описания работы анаэробного биореактора достаточно рассмотрения двухстадийной модели процесса (рис. 1), исходя из которой концентрация органического загрязнения сточной воды пересчитывается в эквивалентную концентрацию глюкозы S.
На вход в биореактор подается сточная вода с эквивалентной концентрацией глюкозы Sin. Двухстадийный процесс анаэробного брожения, протекающий по схеме: S + B1 → P, P + B2 → G с вектором состояний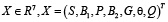 
характеризуется следующей динамикой: в биореактор-смеситель объемом V, м3 в момент времени t подается субстрат с расходом Q(t) = Qin(t), м3сут-1 и концентрацией органических загрязнений S = Sin(t), θ – рабочая температура процесса. На выходе биореактора формируется поток очищенной воды с концентрацией загрязнений Sout(t) = S(t)+P(t), состоящих из остатков исходного субстрата с концентрацией S(t) и промежуточных продуктов анаэробного брожения с концентрацией P(t). В процессе очистки исходное органическое загрязнение проходит стадии кислотогенеза и метаногенеза. В результате жизнедеятельности кислотогенной биомассы с концентрацией B1 образуются промежуточные продукты очистки, которые перерабатываются в биогаз метаногенной биомассой с концентрацией B2. Трофическая цепь двухстадийного процесса анаэробного брожения имеет иерархический вид (знаком «●» здесь обозначена взаимосвязь в паре «хищник – жертва»):
Кислотогенез. Субстрат-жертва (S)●Биомасса-хищник (B1) ⇒ Продукт (P);
Метаногенез. Продукт (P)-жертва (S)●Биомасса-хищник (B2) ⇒ Газ (G).
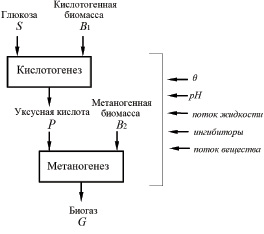
Рис. 1. Схема двухстадийного процесса анаэробного разложения органического загрязнения сточной воды в анаэробном биореакторе
1.2. Анаэробный биореактор со взвешенно-седиментированной биомассой
Рассмотрим для определенности математическое описание вида, структурная схема мониторинга с наблюдателем состояний которого представлена в [5]:
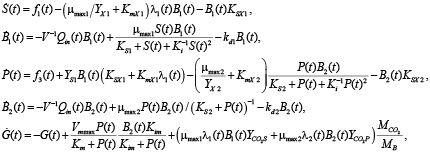
(1)
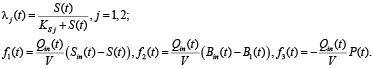
Здесь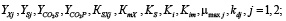 
– кинетические постоянные, определяемые эмпирически с учетом двух групп микроорганизмов – кислотогенов и метаногенов с концентрациями B1 и B2 соответственно.
Функции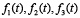 
характеризуют поступление и отвод субстрата, биомассы и продуктов биохимической реакции соответственно.
1.3. Используемый аппарат управления процессами в биореакторах
Математический аппарат, используемый в контексте управления процессами биореактора (принцип максимума Понтрягина (В.В. Кафаров, 1988), релейное управление (А.Н. Кириллов, 2011), АКАР (В.Ю. Невиницын, 2013; Е.К. Грудяева, 2015), ПИ-регулирование (E. Ali, 1999; J. Busch, 2008), скользящие режимы (H.J. Tham, 2003), Nonlinear Model Predictive Control (J. Busch, 2008) и др.), подтверждает нетривиальность проблемы воздействия на биохимические процессы биореактора (обзор проблем управления в [8–10], без претензий на полноту приведенных ссылок):
1) все системы биологической очистки имеют нелинейное описание и наличие возмущений по ряду параметров, динамика частных процессов подчиняется системам уравнений в частных производных, что приводит либо к невозможности непосредственного применения классических алгоритмов управления, либо к громоздкости вычислительных процедур при использовании в реальном режиме времени [11, 12];
2) непосредственное корректное применение классических методов теории оптимального управления возможно только для хорошо формализованных и корректно линеаризованных объектов со всеми вытекающими от операции линеаризации побочными эффектами [8, 9, 11];
3) не существует универсального общего подхода к управлению с наблюдателем состояний сложного объекта (оценкой неизмеряемых непосредственно переменных); имеют место: затруднительная практическая осуществимость; частичная нефизичность и неинтерпретируемость полученных управлений; учет наблюдаемости всех переменных в процессе построения регуляторов [11–13]; неадаптивность самого управления в неустойчивых режимах; необходимость параметризации линеаризации при попытке учесть нелинейность исходного описания в регуляторе.
Ниже представлены два подхода к управлению: первый – эвристический, реализующий стабилизацию САБО в окрестности устойчивого состояния, отвечающего технологическим условиям; второй – аналитический, основан на принципах синергетической теории управления и метода интегральной адаптации, компенсирующий ограниченные возмущения по каналу управления.
Первый подход – эвристический, основан на численном поиске искомой ситуации в имитационной модели и наиболее распространен для сложных систем, но требующий точного знания уравнений динамики всех переменных объекта управления. Второй подход, по мнению авторов статьи, является наиболее перспективным на роль основы общей методологии конструирования энергоэффективного воздействия на сложный объект, функционирующий в неполно определенной среде, обеспечивающий целевой системе робастные свойства.
2. Подход к решению задачи стабилизации на основе целевых инвариантов САБО.
Стационарные состояния системы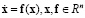 
(состояния равновесия) характеризуются уравнением 
.
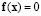Для (1) вектор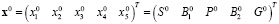 
стационарных состояний соответствует соотношениям
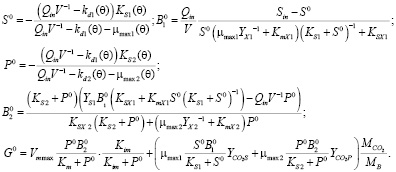(2)
2.1. Исследование устойчивости точки равновесия
Состояние равновесия является устойчивым по Ляпунову, если малое изменение начальных условий объекта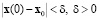 
приведет к малым изменениям состояния с течением времени 
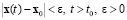, согласно описанию 
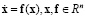. Состоянию равновесия 
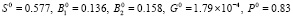, согласно уравнениям (2), сопоставлен вектор 
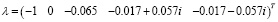собственных значений матрицы Якоби с отрицательными вещественными частями собственных чисел (кроме 2-й координаты), свидетельствующий в целом о его устойчивости.
2.2. Стабилизация САБО в окрестности устойчивого состояния с приемлемыми свойствами на основе численного моделирования
Для заданных входных данных: V (объем реактора), Sin (входная загрязненность), θ (температура) найти значение θ*, обеспечивающей заданную степень очистки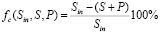 
на выходе реактора, при ограничении на значение гидравлического времени 
.
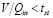1. Зададим начальные значения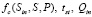 
, удовлетворяющие ограничению 
: 
.
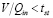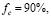
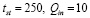2. Вычислим массив значений стационарных точек системы по формулам (2) в соответствии с изменением температуры θ от 25 °C до 45 °C (рис. 2), определяя для каждой i-й стационарной точки значение степени очистки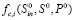 
.
3. Проверяем условие: если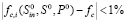 
, запоминаем соответствующую температуру θ, соответствующую заданной степени очистки.
Результат работы программы в соответствии с данным алгоритмом: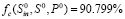 
при θ = 28 °C (рис. 2) и вектором состояния 
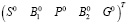с координатами
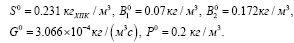
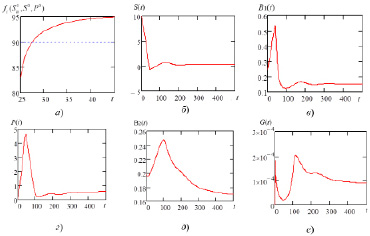
Рис. 2. а) динамика степени очистки на выходе реактора при заданных начальных условиях и выбранном управляющем показателе; б) – е) характер переходных процессов по каждой координате объекта управления (1)
3. Стабилизация САБО в окрестности устойчивого состояния с компенсацией неизвестных возмущений на основе алгоритма интегральной адаптации
(Nonlinear ADaptation (NAD)). Реализация NAD-алгоритма имеет следующие положения [7]:
1. Задание целевых (желаемых) значений для L управляемых переменных.
Пример векторной макропеременной при L = 2 для (1). Основной целью функционирования биореактора в САБО является снижение концентрации органического загрязнения сточной воды до (или ниже) нормативного значения Sнорм. При этом желательно максимально полно преобразовать загрязнения в биогаз. Если G* – расчетное количество биогаза, которое возможно получить, то целевая макропеременная может принять вид
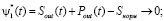
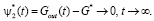
При этом описание (1) преобразуется добавлением/изменением уравнений для организации обратной связи, например, дополнительных уравнений вида
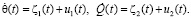(3)
2. Расширение фазового пространства за счет моделирования возмущения, система (1) дополняется уравнениями вида
,
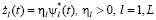где L – размерность вектора управления,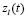 
– аддитивная модель возмущения 
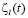по l-му каналу управления, 
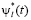– l-я целевая макропеременная.
3. Осуществление классического АКАР-синтеза [7] для полученной замкнутой системы с тем лишь различием, что на конечном этапе синтеза достигаемая l-я цель управления будет иметь описание не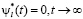 
, а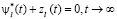 
(подробно в [14]).
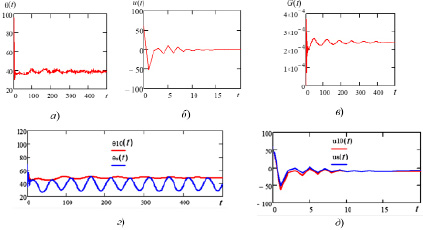
Рис. 3. а), б) форма изменения управляющей переменной, величины воздействия и в) стабилизируемой переменной соответственно, со случайным возмущением N (0;1); г), д)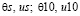 
температура и управления при гармонической помехе и постоянной помехе 
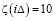соответственно; Δ – настраиваемый интервал дискретизации
Утверждение. Если вид нелинейного описания математической модели процессов биореактора допускает существование классического АКАР-управления без учета возмущения, то существует NAD-управление, на основе которого осуществляется компенсация неизвестных ограниченных аддитивных возмущений по каналам воздействия.
Доказательство утверждения основано на конструктивном NAD-алгоритме [7, 15]. На рис. 3 иллюстрируются робастные свойства NAD-алгоритма для случая L = 1 с управлением по температуре и разными типами возмущений (постоянным, гармоническим, случайным).
Заключение
Постановки задач управления для объектов с нелинейным описанием и заданием целесообразных предельных законов функционирования, отражающих технологические требования к целевой системе, связаны с изучением следующих вопросов:
− математические условия конструирования физичной системы управления;
− условия существования одного или нескольких решений для управления;
− физическая интерпретация локальных функционалов, сопровождающих синтез регуляторов и практическая реализация полученных систем управления.
Для выбираемого воздействия на объект традиционно требуется информация о полном векторе состояния объекта. В рассмотренном здесь объекте (САБО) непосредственному измерению доступны не все координаты, для части координат в реальных системах это либо технически трудно реализуемо, либо физически невозможно, поскольку на скорость и качество химических реакций влияют многие факторы, не все учитываемые в модели. Таким образом, неизбежное наличие немоделируемой динамики не только возможно, но и может играть нежелательную роль, приводящую к неустойчивым состояниям САБО.
Новое направление в теории нелинейного адаптивного управления, реализованное методом интегральной адаптации, на основе которого решена задача компенсации возмущения в объекте (1) по каналу управления, позволяет конструировать робастные системы управления без получения текущей информации об изменении параметров объекта и внешней среды.
Основная идея используемого NAD-алгоритма состоит в введении в каналы управления интеграторов, обеспечивающих подавление кусочно-постоянного возмущения, аддитивно входящего в уравнение с управлением (в установившемся режиме работы системы).
Собирая известные положения:
а) непрерывные функции (возмущения) моделируются решениями некоторых дифференциальных уравнений (обоснование АКАР-синтеза синергетических регуляторов в [13]);
б) любая измеримая ограниченная функция представима как равномерный предел кусочно-постоянных функций –
допустимо применение NAD-алгоритма для любого ограниченного возмущения, не выводящего из условий применимости АКАР-метода. Вопрос только в величине радиуса окрестности целевого множества, требующий отдельного изучения для конкретного вида математической модели.
Исследование выполнено при финансовой поддержке РФФИ № 20-08-00747.
Библиографическая ссылка
Колесникова С.И., Цветницкая С.А., Фоменкова А.А. МЕТОД ИНТЕГРАЛЬНОЙ АДАПТАЦИИ ДЛЯ КОМПЕНСАЦИИ ВОЗМУЩЕНИЙ ПРИ МОДЕЛИРОВАНИИ СИСТЕМЫ АНАЭРОБНОЙ БИОЛОГИЧЕСКОЙ ОЧИСТКИ // Современные наукоемкие технологии. – 2022. – № 5-2. – С. 197-203;URL: https://top-technologies.ru/ru/article/view?id=39170 (дата обращения: 20.04.2024).