Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Григорьева Т.В. 1 Белобородова Т.Г. 2 Иремадзе Э.О. 2

---

1 ФГБОУ ВО «Уфимский государственный нефтяной технический университет

2 ФГБОУ ВО «Башкирский государственный университет»

В настоящее время характер производственного процесса быстро меняется, становится все более сложным, что связано с изменениями в потребительском спросе, сокращением жизненного цикла продукта. Это требует производственных технологий, которые могут легко адаптироваться к таким изменениям. В этом контексте искусственные нейронные сети являются эффективным способом решения проблемы. Большинство производственных процессов регулируются многими переменными параметрами, и по этой причине такие системы имеют случайный, сложный и неопределенный характер. Применение нейронных сетей для моделирования технологических процессов позволит повысить эффективность систем управления качеством, предоставив необходимый объем информации о процессе и дополнительные инструменты исследования, анализа и управления. В статье приводятся результаты моделирования нейронной сети для нахождения оптимальной мощности сушильных устройств, необходимой для полимеризации краски. В качестве моделей была выбрана искусственная нейронная сеть архитектуры многослойный перцептрон. Для построения искусственной нейронной сети использован программный продукт российского производства DeductorStudioAcademic 5.3. Было создано три модели нейросетей и проведен сравнительный анализ их эффективности. Показано, что наибольшую эффективность, одновременно как на обучающем, так и на тестовом множествах исходных данных, показывает искусственная нейронная сеть с 9 нейронами на единственном скрытом слое. Разработанная модель является эффективным инструментом для печатной промышленности.

Статья в формате PDF

676 KB

математическая модель

нейронные сети

нейросетевая модель

многослойный перцептрон

Deductor Studio

корреляционный анализ

1. Галустов Г.Г., Седов А.В. Математическое моделирование и прогнозирование в технических системах: учебное пособие. Ростов н/Д.: Издательство ЮФУ, 2016. 107 с.

2. Домашнев П.А. Разработка и исследование нейросетевых инструментов моделирования и управления сложными технологическими процессами: дис. … канд. техн. наук. Липецк, 2006. 199 с.

3. Григорьева Т.В., Белобородова Т.Г., Барменкова Е.А. Корреляционно-регрессионный анализ выявления факторов, влияющих на производительность компании (на примере пао «газпром») // Материалы 46-й Всероссийской научно-технической конференции молодых ученых, аспирантов и студентов с международным участием. Том 2. (Октябрьский, 26 апреля 2019 г.). Уфа: Издательство Уфимского государственного нефтяного технического университета, 2019. С. 77–80.

4. Воловиков Б.П. Стратегическое прогнозирование развития промышленного предприятия на основе метода нейронных сетей и аппарата нечеткой логики // Стратегический менеджмент. 2011. № 4. С. 256–268.

5. Головко В.А., Краснопрошин В.В. Нейросетевые технологии обработки данных: учеб. пособие. Минск: БГУ, 2017. 263 с.

6. Ясницкий Л.Н. Интеллектуальные системы. М.: Лаборатория знаний, 2016. 221 с.

7. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы / Пер. с польск. И.Д. Рудинского. 2-е изд., стереотип. М.: Горячая линия – Телеком, 2013. 384 с.

8. Сток Д., Уотсон М. Анализ статистических данных: учебник / Под науч. ред. М.Ю. Турунцевой; пер. с англ. В. Акимова, Б. Гафарова, М. Леонова и др. М.: Издательский дом «Дело» РАНХиГС, 2015. 865 с.

9. Никонов О.И., Кругликов С.В., Медведева М.А. Математическое моделирование и методы принятия решений: учебное пособие. 2-е изд., стер. М.: Флинта, Изд-во Урал. ун-та, 2017. 100 с.

В настоящее время характер производственного процесса меняется с большой скоростью, становится все более изощренным и происходят постоянные изменения из-за изменений в потребительском спросе и сокращения жизненного цикла продукта. Это требует производственных технологий, которые могут легко адаптироваться к таким изменениям. В этом контексте искусственные нейронные сети являются мощной технологией для решения этой проблемы. Использование искусственных нейронных сетей также широко используется для мониторинга и контроля процессов. Качество процесса может быть обеспечено только в ходе мониторинга процесса посредством надлежащих измерений.

Практические разработки применения нейронных сетей для моделирования различного рода инженерных систем показывают, что нейросетевые модели точнее регрессионных и лишены ряда имеющихся у регрессионных моделей недостатков [1, 2]. Применение нейронных сетей для моделирования технологических процессов позволит повысить эффективность систем управления качеством, предоставив необходимый объем информации о процессе и дополнительные инструменты исследования, анализа и управления.

В соответствии с вышеизложенным целью работы являлось создание нейросетевой модели, предназначенной для нахождения инфракрасного светового потока полиграфического процесса оксидации краски. Для достижения поставленной цели изучили применение нейросетевого моделирования в решении задач технологического процесса, построили наиболее подходящую модель нейронной сети для нахождения оптимальной мощности сушильных устройств, необходимой для полимеризации краски; сравнили результаты, полученные на основе нейронной сети с их реальными значениями. В качестве объекта исследования работы избраны технологические процессы оксидации краски.

Научной новизной представляемой работы является построение нейросетевой модели, предназначенной для нахождения инфракрасного светового потока полиграфического процесса оксидации краски.

Практическая значимость исследования заключается в том, что разработанный на основе построенной нейросетевой модели программный продукт дает возможность с небольшой ошибкой устанавливать технологические параметры сушильных устройств, необходимые для оксидации краски. Благодаря этому разработанный проект является эффективным инструментом в печатной промышленности.

Материалы и методы исследования

В качестве исходных данных для построения математической модели инфракрасного светового потока полиграфического процесса оксидации краски использованы результаты работы типографского станка в течение трех месяцев. Экспериментальные данные были занесены в электронную таблицу для последующего преобразования в формат CSV с разделителем semicolon. Общий объем составил 300 записей, каждая из которых содержала следующие значения: номер эксперимента; скорость, м/с; мощность, % (максимум 158 кВт); температура окружающей среды, °C; влажность, %; брак, %; тираж, шт.; независимый брак, шт.; суммарный брак, шт.

Целью построения модели процесса печати является снижение себестоимости изготовления печатной продукции путём снижения доли брака. Под браком подразумевается только та доля печатной продукции, которая оказалась непригодна вследствие неоптимального инфракрасного потока для оксидации краски. Для нахождения доли контролируемого брака составлена формула (1) как разница между долями суммарного и независимого брака:

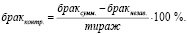(1)

Переход к относительным величинам позволяет отказаться от такого параметра, как тираж. Стоит отметить, что данная величина является постоянной характеристикой оборудования и, таким образом, не может рассматриваться в качестве регулирующего параметра при оптимизации. Для всех записей в исходной электронной таблице был произведен расчёт контролируемого брака по вышеприведённой формуле.

Максимальная мощность инфракрасной сушки, которую можно получить на рассматриваемом оборудовании, составляет 158 кВт. Значения мощности из исходных данных были переведены из относительной величины (power) в абсолютную (power2) по формуле

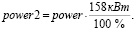(2)

В качестве входных регулируемых параметров остались четыре значения: скорость (speed), м/с; температура окружающей среды (temperature), °C; влажность (humidity); мощность (power2), кВт. В качестве выходного параметра рассматриваем контролируемый брак (defect2), %. Фрагмент данных для построения модели представлен в табл. 1. Статистические данные по всем параметрам модели приведены в табл. 2.

С целью устранения незначащих входных параметров выполнен корреляционный анализ Пирсона [3], результаты которого представлены в табл. 3.

Для каждого из входных параметров наблюдается отрицательный коэффициент корреляции Пирсона. Это свидетельствует о том, что в общем случае наблюдается обратная значимость между долей контролируемого брака и каждым из параметров: скоростью, температурой, влажностью и мощностью. Однако тот факт, что коэффициенты корреляции не равны 1, показывает, что зависимость не является точно линейной, а, следовательно, возможно наличие экстремальных точек. Данный вывод согласуется с теоретическими сведениями.

Таблица 1

Фрагмент экспериментальных данных

Таблица 2

Статистика параметров модели

Таблица 3

Результаты корреляционного анализа

Согласно справочным данным, критическое значение t-критерия Стьюдента для 295 степеней свобод и доверительной вероятности 95 % составляет 1,968. Полученные данные указывают, что все входные параметры не менее критического значения, следовательно, являются значащими для данной модели.

Математическая модель полиграфического процесса. Для обучения искусственных нейронных сетей применяется набор исходных данных, рассмотренных выше. В качестве моделей была выбрана искусственная нейронная сеть архитектуры многослойный перцептрон. Это нейросеть прямого распространения показала наилучшую эффективность для решения задач аппроксимации непрерывных параметров. К тому же многослойный перцептрон отличается простотой строения, выработанными эффективными алгоритмами обучения и высоким быстродействием [4–6].

Для построения искусственной нейронной сети использован программный продукт российского производства Deductor Studio Academic 5.3. Редакция Academic является бесплатной академической версией. Поддерживаются только три источника и приемника данных: Deductor Warehouse, Deductor Data File и текстовые файлы.

Создание нейронной сети начинается с импорта файла с исходными данными. В отрывшемся окне программы «Сценарии» открывается контекстовое меню и выбирается «Мастер импорта». Выбирается пункт Text – Тестовый файл (Direct). На втором шаге в окне мастера импорта выбирается ранее созданный CSV файл, кодировка ASCII (MSWindows). Флаг «Первая строка является заголовком» оставляется выбранным. Пункт «Начать импорт со строки» также оставляется равным «1». На третьем шаге параметры формата импорта оставляются неизменными. На четвертом шаге символом разделителем устанавливается пункт «Точка с запятой». Флаг «Считать последовательные разделители одним» оставляется неактивным. На шестом шаге настраиваются параметры столбцов. Для столбцов speed, temperature, humidity, power2 устанавливаются: Тип данных – «Вещественный»; Вид данных – «Непрерывный»; Назначение – «Входное». Для столбца defect2 устанавливаются: Тип данных – «Целый»; Вид данных – «Непрерывный»; Назначение – «Выходное». На седьмом шаге завершается процесс импорта данных из текстового файла. На восьмом шаге устанавливаются следующие флаги: «Таблица», «Статистика», «Сведения». На девятом шаге происходит окончание импорта.

Обучение нейросетей происходит следующим образом: для создания нейросети выбираем соответствующий файл исходных данных, расположенный в области «Сценарии». В появившемся контекстовом меню выбирается пункт «Мастер обработки». В появившемся окне в группе «DataMining» выбирается пункт «Нейросеть» – «Многослойная нейронная сеть». Так как в процессе импорта все поля уже были настроены, то оставляем поля без изменений, активизируем кнопку «Настройка нормализации».

Нормализация столбца speed будет происходить следующим образом: Привести к диапазону. Диапазон значений – активно; Минимум – 0; Максимум – 4; Параметры линейного преобразования: Привести к диапазону – активно; Минимум диапазона – -1; Максимум диапазона – 1.

Нормализация столбца temperature: Привести к диапазону. Диапазон значений – активно; Минимум – 0; Максимум – 28; Параметры линейного преобразования: Привести к диапазону – активно; Минимум диапазона – -1; Максимум диапазона – 1.

Нормализация столбца humidity: Привести к диапазону. Диапазон значений – активно; Минимум – 0; Максимум – 100; Параметры линейного преобразования: Привести к диапазону – активно; Минимум диапазона – -1; Максимум диапазона – 1.

Нормализация столбца power2: Привести к диапазону. Диапазон значений – активно; Минимум – 0; Максимум – 158; Параметры линейного преобразования: Привести к диапазону – активно; Минимум диапазона – -1; Максимум диапазона – 1.

Нормализация столбца defect2: Привести к диапазону. Диапазон значений – активно; Минимум – 0; Максимум – 100; Параметры линейного преобразования: Привести к диапазону – активно; Минимум диапазона – 0; Максимум диапазона – 1.

На третьем шаге задается размер тестового и обучающего множеств. «Способ разделения исходного множества данных» оставляется равным «Случайно». Размеры множеств в процентах: обучающее: 80,00 % (240 строк); тестовое:20,00 % (60 строк).

На четвертом шаге настраивается конфигурация создаваемой нейросети. Так как нормализация выходного поля производилась в интервале от 0 до 1, выбираем в качестве активационной функцию сигмоиду, логистическую функцию, область значений которой совпадает с данным диапазоном.

Необходимое количество нейронов в скрытых слоях перцептрона можно определить по формуле (3), являющейся следствием из теорем Арнольда – Колмогорова – Хехт – Нильсена [7]:

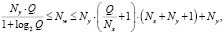(3)

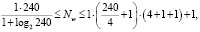
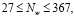
где Ny – размерность выходного сигнала (Ny = 1); Nw – необходимое число синаптических связей; Nx – размерность входного сигнала (Nx = 4); Q – число элементов множества обучающих примеров (Q = 240).

Оценив с помощью формулы (3) необходимое число синаптических связей Nw , можно рассчитать необходимое число нейронов в скрытых слоях. Например, число нейронов в скрытых слоях двухслойного перцептрона будет равно

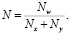(4)

Минимальное число нейронов:

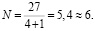
Максимальное число нейронов:

.

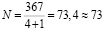Для обучения первой нейросети выберется минимальное значение числа нейронов на единственном скрытом слое – 6 (рис. 1, а). На пятом шаге (рис. 1, б) оставляется значение по умолчанию: шаги спуска и подъема и алгоритм ResilientPropagation.

На шестом шаге настраиваются условия остановки обучения. Считается пример распознанным, если ошибка в вычислении доли брака defect2 составила менее 1 %. Так как выходной параметр принимает значения в интервале [0; 100], а линейное преобразование осуществляется из диапазона [0; 1], то нормированное значение ошибки будет составлять

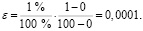(5)

Устанавливается значение ошибки равным 0,0001. Количество эпох увеличивается в 10 раз, устанавливая равным 100000 (рис. 2).

На седьмом шаге завершается процесс обучения (рис. 2). Обучение завершилось после превышения количества эпох. Время обучения 1 мин 30 с (90 с).

На восьмом шаге «Определение способов отображения» выбираются все пункты следующих групп: Data Mining, Табличные данные, Общие. Результаты обучения нейросети представлены на рис. 3.

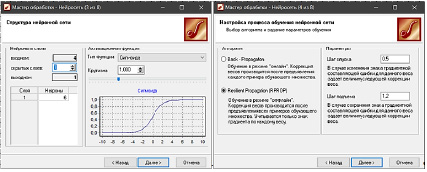
а б

Рис. 1. Настройка процесса обучения нейронной сети

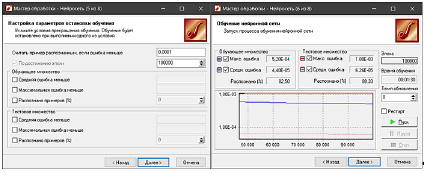
Рис. 2. Настройка параметров остановки обучения и результат обучения сети 4х6х1

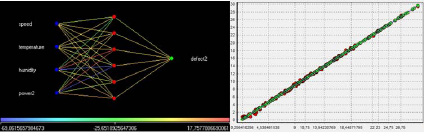
Рис. 3. Графы и диаграмма рассеивания нейросети 4х6х1

Таблица 4

Сравнение нейросетей

Создается ещё одна нейросеть с одним скрытым слоем. Параметры будут аналогичны предыдущей сети за исключением числа нейронов на скрытом слое – оно равно максимальному значению – 73 нейрона. Обучение было прервано на 2488 эпохе ввиду начавшегося переобучения модели. Эффект переобучения выражается прекращением снижения значения средней ошибки на тестовом множестве исходных данных и начинающимся неуклонным ростом этого значения. Время обучения 1 мин 8 с (68 с).

Третья нейросеть создается с двумя скрытыми слоями. Для сравнения также возьмем максимальное число синаптических связей, равное 367. Количество нейронов в обоих скрытых слоях примем одинаковым. Тогда формула количества синаптических связей равна

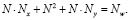(6)

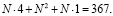
Решая полученное уравнение, находим его положительный корень: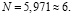

Таким образом, создаем сеть с двумя скрытыми слоями по 6 нейронов в каждом. Остальные настройки остаются аналогичными предыдущим нейросетям. Обучение было прервано на 54905 эпохе ввиду начавшегося переобучения модели. Время обучения 3 мин 24 с (204 с). Сравнение результата обучения всех трех нейросетей приведено в табл. 4.

Анализируя полученные в табл. 4 результаты, можно сделать вывод, что использование двух и более скрытых слоёв нецелесообразно. Получающиеся модели обладают значительно более низкой эффективностью на тестовых данных, что свидетельствует о явлении переобучения. Данное явление обусловлено чрезмерно высокой размерностью сети для данного набора обучающих данных.

Таким образом, поиск оптимальной нейросетевой модели следует продолжать среди многослойных перцептронов с одним скрытым слоем. Количество нейронов на данном слое было оценено в интервале [6, с. 73]. Поиск осуществляли методом расчётной сетки в логарифмическом масштабе [8; 9]. Так, разбивая интервал на 4 участка, получали точки: 11, 21, 39. Определив, что наилучшие результаты дала нейронная сеть с 1 нейронами на скрытом слое, методом бисекции всё также в логарифмическом масштабе для каждой нейросети вычисляли долю распознанных примеров на обучающем и тестовом множествах. Результаты представлены в табл. 5.

Исходя из полученных данных, наибольшую эффективность, одновременно как на обучающем, так и на тестовом множествах исходных данных, показывает искусственная нейронная сеть с 9 нейронами на единственном скрытом слое (рис. 4). Для данной сети обучение завершилось после превышения количества эпох. Время обучения 2 мин 2 с (122 с).

Провели анализ эффективности нейросетевой модели. Среднеквадратическое отклонение для задачи множественной регрессии определяется по формуле

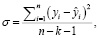(7)

где yi – фактическое значение выходной переменной в i-м примере; 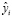– расчётное значение выходной переменной в i-м примере; n – количество примеров; k – количество факторов.

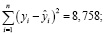
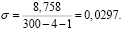
Стандартное отклонение находим по формуле

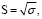(8)

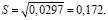
Таблица 5

Сравнение нейросетей с одним скрытым слоем

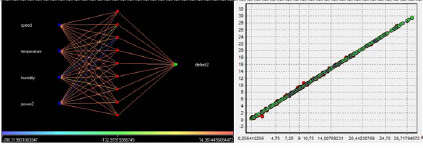
Рис. 4. Граф и диаграмма рассеивания нейросети 4х9х1

Для оценки качества нейросетевой модели используется множественный коэффициент корреляции, вычислив его через коэффициент детерминации

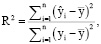(9)

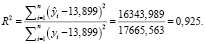
Следовательно, около 92,5 % вариации зависимой переменной учтено в нейросетевой модели и обусловлено влиянием включенных факторов.

Скорректированный коэффициент детерминации вычисляется по формуле

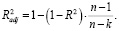(10)

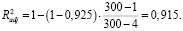
Множественный коэффициент корреляции составит: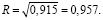

Результаты исследования и их обсуждение

Таким образом, было показано, что применение нейросетей для решения задач аппроксимации зависимостей математических моделей является высокоэффективным подходом и наиболее действенным. Однако в процессе поиска оптимальной размерности нейронной сети следует учитывать эффект переобучения, который, несмотря на высокую точность для обучающих примеров, приводит к тому, что нейросеть перестаёт адекватно описывать исследуемый процесс. В ходе построения нейросетевой модели в данной работе учитывался риск присутствия данного эффекта и в случае его возникновения процесс обучения прекращался.

Заключение

Таким образом, в качестве математической модели исследуемого процесса была выбрана искусственная нейронная сеть типа многослойный перцептрон с одним скрытым слоем. Для программной реализации обученной нейронной сети с целью её дальнейшего использования в составе как клиентского приложения, так и в составе программного обеспечения программируемого логического контроллера (ПЛК), был выбран язык программирования C#.

Практическая значимость работы заключается в том, что разработанный программный продукт на основе созданной нейронной сети дает возможность с небольшой ошибкой устанавливать мощность инфракрасного потока, необходимого для наилучшей оксидации краски при различных внешних факторах. Благодаря этому разработанная модель является эффективным инструментом в печатной промышленности.

Библиографическая ссылка