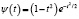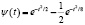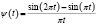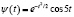Методы теоретической и прикладной статистики данных нашли широкое применение в различных сферах, среди которых можно выделить оптимизацию сложных технологических процессов, сертификацию технических систем и изделий, геофизические исследования грунтовых оснований для получения информации о распространении талых зон на вечномерзлых грунтах с целью обеспечения устойчивости зданий и сооружений. Возникающие в реальной жизни задачи нередко заставляют исследователя сталкиваться с необходимостью поиска зависимости между входными данными, задающими условия функционирования, и выходными данными, которые характеризуют изучаемый объект. Решение таких задач может быть выполнено путем построения регрессионных моделей, и один из этапов состоит в оценивании неизвестных параметров. Такой подход позволяет не просто восстановить исходную зависимость, но и выполнять прогнозирование поведения изучаемого объекта.
Классические методы оценивания неизвестных параметров регрессионных зависимостей позволяют получать достаточно корректные и качественные результаты только при условии, что имеются достоверные предположения о свойствах случайной компоненты [1]. Одним из таких способов определения неизвестных оценок является метод максимального правдоподобия. Применение данного метода возможно при условии, что имеется достоверная информация о виде распределения случайных ошибок наблюдения [1]. Предположение о нормальности распределения ошибок наблюдения позволяет применить метод наименьших квадратов и тем самым упростить поиск оценок. Но на практике в большинстве случаев распределение случайной ошибки нельзя считать нормальным. В связи с этим целью данной работы является разработка универсального адаптивного алгоритма оценивания параметров регрессионных моделей, позволяющего получать корректные результаты во многих практически реализуемых задачах. Предложенный авторами подход основан на вейвлет-анализе [2, 3], который широко используется для аппроксимации различных функций [4, 5]. Применение различных материнских вейвлетов позволило создать целый ряд новых адаптивных алгоритмов оценивания параметров регрессионных зависимостей, обеспечивающих получение качественных результатов для большого числа реальных ситуаций, в том числе при отсутствии известных предположений о свойствах случайной компоненты.
Постановка задачи и основные предположения
Пусть регрессионное уравнение принимает вид
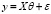, (1)
где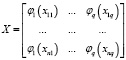 
– матрица значений функций регрессионной модели, 
; 
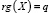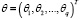– оцениваемые неизвестные параметры модели; φi(x) – известные вещественные функции; xij – значения входных факторов в n наблюдениях; 
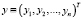– вектор значений отклика; 
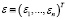– вектор независимых случайных ошибок, q – число неизвестных параметров; n – число проведенных экспериментов.
Считаем, что вектор ошибок наблюдений εi состоит из независимых одинаково распределенных случайных величин с функцией плотности h(t), для которых выполняется
E(εi) = 0, D(εi) = σ2 < ∞.
Требуется, по имеющимся значениям отклика и входных данных, выполнить наиболее точное оценивание вектора неизвестных параметров регрессионного уравнения (1).
Оценка функции плотности распределения с помощью вейвлет-анализа
Пусть на произвольном отрезке [c,d] задана выборка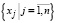 
, состоящая из независимых значений случайной величины ξ, причем 
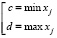. Закон и функция плотности распределения h(t) случайной величины ξ считаются неизвестными. Тогда согласно [4, 5] оценка функции плотности 
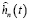случайной величины ξ может быть представлена в виде ряда
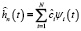, (2)
где N – параметр сглаживания (количество членов ряда),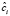 
– коэффициенты разложения по ортонормированным базисным функциям ψi(t), выражающиеся в следующем виде:
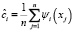. (3)
Принимая во внимание соотношение (3), запишем выражение для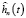 
:
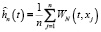, (4)
где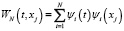 
.
Согласно [4, 5] ортонормированная система функций ψi(t) определена на [0,1] и выражается соотношением
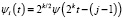, (5)
где k ≥ 0,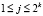 
, 
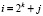, ψi(t) – материнский вейвлет [4, 5]. Выражение (5) выполняется, если i > 1. В случае i = 1 получаем, что 
.
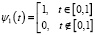В таблице представлены примеры различных материнских вейвлетов.
Примеры материнских вейвлетов
|
Вейвлет-функция |
Аналитическая запись |
|
«Мексиканская шляпа» |
|
|
DOG-вейвлет |
|
|
LITTLEWOOD & PALEY |
|
|
Морле |
|
Отметим, что необходимо перейти от ортонормированной на [0,1] системы базисных функций ψi(t) к системе функций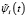 
ортонормированной на отрезке, который совпадает с областью определения случайной величины ξ. Переход от системы ψi(t) к системе 
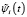согласно [6, 7] выполняется с помощью следующего соотношения:
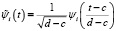. (6)
Тогда вейвлет-оценка функции плотности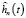 
случайной величины ξ определяется соотношением (4) по ортонормированным базисным функциям 
.
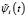Ранее авторами было исследовано качество восстановления функции плотности распределения на основе базисных вейвлетов, приведенных в таблице. С некоторыми результатами исследования можно познакомиться в [6–9]. Выводы, сделанные в результате вычислительных экспериментов, позволили предположить возможность применения вейвлет-оценок функции плотности при оценивании неизвестных параметров регрессионных моделей.
Алгоритм оценивания параметров регрессионных моделей
Рассмотрим задачу оценивания параметров регрессионного уравнения (1), для решения которой воспользуемся методом максимального правдоподобия [10]. Будем считать, что уравнение регрессии (1) является истинным. Значения остатков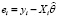 
(Xi – i-я строка матрицы X) являются независимыми случайными величинами с плотностью распределения h(ei, θ), что следует из предположения о независимости случайных ошибок. Тогда логарифмическая функция правдоподобия принимает вид
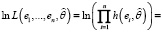
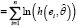. (7)
Приведем пошаговый алгоритм, который позволит выполнять оценивание параметров регрессионных моделей на основе вейвлетов:
Шаг 1. Определить начальное значение вектора неизвестных параметров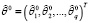 
уравнения (1), l = 0, где l – номер итерации. В данном алгоритме предполагается использование метода наименьших квадратов [10] для определения начального приближения.
Шаг 2. Вычислить значения остатков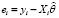 
регрессионной зависимости.
Шаг 3. Получить оценку функции плотности распределения с помощью соотношения (4) по ортонормированным базисным функциям (6).
Шаг 4. Определить значение логарифмической функции правдоподобия (7).
Шаг 5. Найти значение оценки вектора неизвестных параметров
.
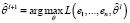Шаг 6. Итерационный процесс завершается, если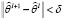 
, где δ – заданная погрешность вычисления. Если же 
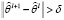, то выполняется переход на шаг 2 при условии l = l + 1.
Оценивание параметров регрессионных моделей с использованием вейвлетов
Поиск решения для задачи оценивания параметров регрессионной зависимости (1) может быть выполнен с помощью вычислительной схемы алгоритма, предложенного выше, где логарифмическая функция правдоподобия выражается соотношением (7) с использованием различных материнских вейвлетов, представленных в таблице.
Ранее на основе вейвлета LITTLEWOOD & PALEY (таблица) авторами была получена система функций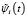 
[8], ортонормированная на произвольном отрезке [c,d], которая выражается следующим соотношением:
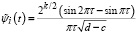, (8)
где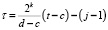 
, а значения i, k, j определяются как в (5).
Вейвлет-оценка функции плотности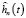 
с использованием вейвлета LITTLEWOOD & PALEY определяется разложением (4) по ортонормированным базисным функциям (8). Принимая во внимание (8) и тот факт, что ошибки наблюдений независимы, функцию правдоподобия (7) можно записать в следующем виде:
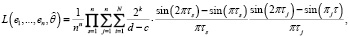(9)
где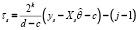 
, 
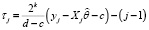, а i, k, j такие же, как в (5).
Логарифмическое представление (9) выражается соотношением
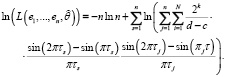(10)
В работе [9] с помощью вейвлета Морле (таблица) авторами была построена система функций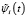 
, ортонормированная на произвольном отрезке [c,d], которая представима в виде
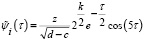, (11)
где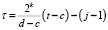 
, а значения i, k, j такие же, как в (5).
Параметр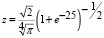 
и получен авторами в работе [8].
Соотношение (4), где базисные функции определяются выражением (11), является оценкой функции плотности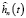 
случайной величины на основе вейвлета Морле. Тогда используя ортонормированную систему (11) и учитывая, что ошибки наблюдений независимы, функцию правдоподобия (7) можно записать в следующем виде:
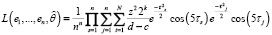, (12)
где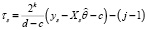 
, 
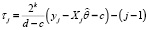, а i, k, j такие же, как в (5), а z из (11).
Логарифмическое представление (12) выражается соотношением
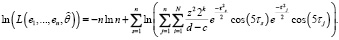(13)
Ортонормированная система функций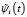 
на произвольном отрезке [c,d] с использованием DOG вейвлета (таблица) получена авторами ранее в работе [7] и выражается соотношением
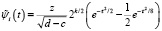, (14)
где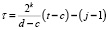 
, а значения i, k, j такие же, как в (5).
Значение параметра получено авторами в работе [6] и определяется соотношением
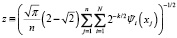. (15)
Вейвлет-оценка функции плотности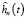 
с использованием DOG вейвлета выражается разложением (4) по ортонормированным базисным функциям (14). Функция правдоподобия (7) на основе DOG вейвлета принимает вид
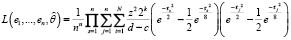, (16)
где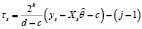 
, 
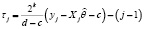, а i, k, j такие же, как в (5).
Логарифмическое представление (16) выражается соотношением
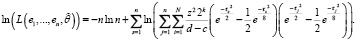(17)
Ортонормированная система функций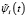 
на произвольном отрезке [c,d] с использованием вейвлета «Мексиканская шляпа» (таблица) была получена авторами в работе [6] и выражается соотношением
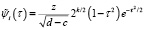, (18)
где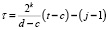 
, а значения i, k, j определяются как в (5). Значение параметра z выражается соотношением (15).
Разложение (4) по ортонормированным базисным функциям (18) определяет вейвлет-оценку функции плотности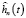 
случайной величины с помощью вейвлета «Мексиканская шляпа». Функция правдоподобия (7), построенная с учетом соотношения (18) и того, что ошибки наблюдений независимы, принимает вид
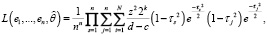(19)
где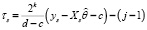 
, 
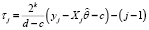, а i, k, j такие же, как в (5), z из (15).
Логарифмическое представление (19) выражается соотношением
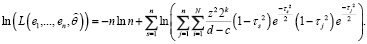(20)
Покажем, что представленная вычислительная схема алгоритма оценивания параметров регрессионных моделей, где логарифмическая функция правдоподобия выражается одним из предложенных выше соотношений, соответствующих различным вейвлетам, обеспечивает получение качественных результатов при различных условиях.
Результаты вычислительных экспериментов
Исследуем предложенный выше алгоритм оценивания неизвестных параметров θ регрессионной зависимости (1) на основе различных материнских вейвлетов с помощью методов статистического моделирования. Рассмотрим регрессионную зависимость, выражающуюся в следующем виде:
y = θ1 + θ2x + θ3x2 + ε. (21)
Отметим, что значения входных факторов xij регрессионного уравнения (21) определялись из отрезка [–4, 4], количество неизвестных параметров равно 3, а их истинные значения: θ1 = 4, θ2 = –9, θ3 = 2. Значения вектора ошибок наблюдений εi моделировались независимыми с функцией распределения вида
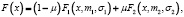(22)
где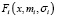 
– функция нормального распределения с математическим ожиданием mi и дисперсией 
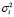; i = 1,2, 
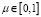– параметр смеси. При выполнении вычислительных экспериментов будем считать m1 = m2 = 0.
Отметим, что моделирование ошибки выполняется при различной степени отклонения от нормального распределения. Доли наблюдений с дисперсиям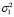и 
и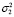 
в выборке определяются с помощью параметра μ, где при μ = 0 и μ = 1 распределение ошибки будет нормальным. В процессе моделирования предполагалось, что 
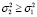, а значения дисперси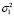й 
и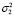 
задавались через значения уровня шума [11], который определяется соотношением
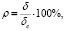(23)
где δ – дисперсия ошибки,
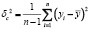– интенсивность сигнала.
Определение точности оценивания параметров выполнялось с помощью L1 нормы отклонений оценок неизвестных параметров от истинных значений
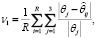(24)
где R – число выполненных вычислительных экспериментов,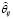 
– оценка j-го параметра регрессионной зависимости (21) в i-ом вычислительном эксперименте.
Количество вычислительных экспериментов для различных комбинаций μ и ρ варьировалось от 100 до 500. Варьирование значения параметра смеси μ в диапазоне от 0 до 0,5 с шагом 0,05 позволило исследовать точность оценивания неизвестных параметров уравнения (21) при разной степени отклонения распределения случайной ошибки от нормального распределения. Моделирование исходных данных выполнялось в соответствии с регрессионной зависимостью (21), а оценивание неизвестных параметров этой модели разработанным алгоритмом на основе различных материнских вейвлетов. Кроме того, вычисление оценок выполнялось методом наименьших квадратов и методом полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения [12]. Точность оценивания определялась значением показателя v1.
Результаты исследования точности оценивания неизвестных параметров уравнения (21) представлены на рис. 1 для объема выборки 200 и на рис. 2 для объема выборки 500, при фиксированном уровне шума ρ1 = 10% и ρ2 = 100%. Вычисление нормы отклонения v1 проводилось с усреднением по 100 вычислительным экспериментам.
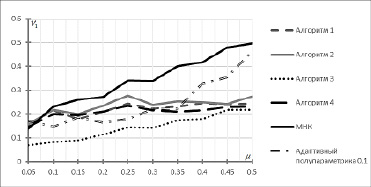
Рис. 1. Значение нормы отклонений в зависимости от μ, объем выборки – 200
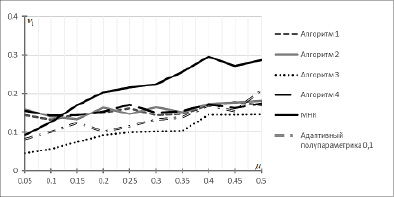
Рис. 2. Значение нормы отклонений в зависимости от μ, объем выборки – 500
Для удобства обозначим адаптивный алгоритм на основе вейвлета LITTLEWOOD &PALEY как алгоритм 1, где наилучшее значение параметра сглаживания установлено в [8] и равно N = 5; адаптивный алгоритм на основе вейвлета Морле – как алгоритм 2, где наилучшее значение параметра сглаживания установлено в [9] и равно N = 10; адаптивный алгоритм на основе вейвлета DOG – как алгоритм 3, где наилучшее значение параметра сглаживания установлено в [7] и равно N = 34; адаптивный алгоритм на основе вейвлета «Мексиканская шляпа» – как алгоритм 4, где наилучшее значение параметра сглаживания установлено в [6] и равно N = 8.
Из рис. 1 и 2 видно, что при значениях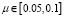 
, алгоритмы 1, 2, 4, оценивания неизвестных параметров регрессионной зависимости, основанные на вейвлет-анализе, имеют не очень высокую точность, несколько уступая методу наименьших квадратов и методу полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения. При μ = 0.05 и объеме выборки 500 значение показателя v1, полученное в результате применения метода наименьших квадратов, на 40 % меньше значений v1, полученных при использовании алгоритмов 2 и 4, и на 36 % меньше значения v1, полученного при использовании алгоритма 1. Аналогичный результат при μ = 0.05 и объеме выборки 500 наблюдается для значения v1, полученного при использовании метода полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения, 47 % и 42 % соответственно. Отметим, что для выборки объёмом 200 при μ = 0.05 значение показателей v1, полученных в результате применения метода наименьших квадратов и метода полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения, меньше значений v1, полученных при использовании алгоритмов 1, 2 и 4 (рис. 1). С ростом значений μ, то есть с ростом числа грубых ошибок наблюдений в исходных данных, алгоритмы на основе вейвлетов дают более точную оценку параметров регрессионной модели в сравнении с методом наименьших квадратов и методом полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения. При μ = 0.5 и объеме выборки 500 нормы отклонений v1, полученные при использовании алгоритмов 1 и 4, меньше на 43 % нормы отклонения v1, полученной при оценивании параметров методом наименьших квадратов, и на 24 % меньше нормы отклонения v1, полученной при применении метода полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения. Значение нормы отклонения v1 при μ = 0.5, объеме выборки 500 и использовании алгоритма 2 на 39 % меньше значения v1, полученного при оценивании параметров регрессионной модели методом наименьших квадратов, и на 19 % меньше нормы отклонения v1, полученной при применении метода полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения. Для выборки объёмом 200 при μ = 0.5 значение показателей v1, полученных при использовании алгоритмов 1, 2 и 4 меньше значений v1, полученных в результате применения метода наименьших квадратов и метода полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения (рис. 1). Наилучшее качество оценивания неизвестных параметров уравнения (21) получается в результате использования в алгоритме в качестве базисного вейвлета DOG вейвлета (алгоритм 1), причем как при малых значениях параметра μ, так и близким к 0.5. При μ = 0.05 и объеме выборки 500 значение показателя v1, полученного при использовании алгоритма 3, на 44 % меньше значения v1, полученного при оценивании параметров регрессионной модели методом наименьших квадратов, и на 38 % меньше нормы отклонения v1, полученной при применении метода полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения. При μ = 0.5 и объеме выборки 500 значение показателя v1, полученного при использовании алгоритма 3, на 46 % меньше значения v1, полученного при оценивании параметров регрессионной модели методом наименьших квадратов, и на 29 % меньше нормы отклонения v1, полученной при применении метода полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения. Отметим, что для выборки объемом 200 при μ = 0.05 и при μ = 0.5 алгоритм 1 имеет более высокую точность по сравнению с методом наименьших квадратов и методом полупараметрического восстановления функции плотности на основе обобщенного лямбда-распределения (рис. 1). Таким образом, алгоритмы оценивания, основанные на таких материнских вейвлетах, как Морле, LITTLEWOOD&PALEY, DOG и «Мексиканская шляпа», показывают хорошую точность оценивания как для выборок с объемом, равным 200, так для выборки, объем которой равен 500.
В данной статье рассмотрено применение вейвлет-анализа при оценивании неизвестных параметров регрессионных моделей с помощью метода максимального правдоподобия. Предложены алгоритмы оценивания неизвестных параметров θ регрессионной зависимости, основанные на различных материнских вейвлетах. Для каждого базового вейвлета получено выражение логарифмической функции правдоподобия. Установлено, что такой подход дает ряд преимуществ при отсутствии известных предположений о свойствах случайной компоненты. Результаты численного моделирования подтвердили возможность применения теории вейвлетов для оценивания неизвестных параметров регрессионных моделей.
Библиографическая ссылка
Тимофеев В.С., Исаева Е.В. ОБ ОЦЕНИВАНИИ ПАРАМЕТРОВ РЕГРЕССИОННЫХ МОДЕЛЕЙ С ИСПОЛЬЗОВАНИЕМ ВЕЙВЛЕТОВ // Современные наукоемкие технологии. – 2022. – № 4. – С. 114-121;URL: https://top-technologies.ru/ru/article/view?id=39118 (дата обращения: 23.11.2024).