Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ожогова Е.В. 1 Лубенцова Е.В. 1 Лубенцов В.Ф. 1

---

1 ФГБОУ ВО «Кубанский государственный технологический университет»

С учетом динамики тепловых потоков, создающих возмущение на температуру среды через поверхность стенки нагревателя, формализована математическая модель нагревателя, используемого для регулирования температуры среды процесса анаэробного сбраживания в биореакторе. Получение модели основано на уравнениях переноса тепла через стенку с применением классического метода решения задачи теплофизики – метода Фурье при граничных условиях для случая конвективного механизма теплоотдачи. При этом в уравнениях учтены критерии Био, характеризующие неравномерность температурного поля, и критерий Фурье, характеризующий нестационарность процессов. Приведены полученные расчетные области значений параметров массивности в зависимости от коэффициентов теплоотдачи конвекцией в стационарном режиме со стороны рабочей среды и со стороны окружающей среды для различных значений толщины стенки нагревателя и коэффициента теплопроводности изотропного материала стенки. Практическая ценность работы состоит в том, что, используя рассчитанные области значений параметров массивности, получены значения постоянной времени модели при конвективном механизме теплоотдачи, характеризующей инерционность при регулировании температуры с помощью трубчатого нагревателя. Полученные расчетные значения позволяют, зная свойства материала стенки, оценить рациональную толщину стенки нагревателя, обеспечивающую минимальную инерционность при фиксированной интенсивности нагрева среды. В случае фиксированной толщины стенки можно выбрать тип нагревателя, изготовленного из материала, обладающего определенными (требуемыми) теплофизическими свойствами. Полученная в работе модель использована при синтезе и анализе системы регулирования температуры трубчатого электрического нагревателя в биореакторе.

Статья в формате PDF

395 KB

математическая модель

нагреватель

теплоперенос

критерии Био

постоянная времени

1. ГОСТ Р 53790-2010 Нетрадиционные технологии. Энергетика биоотходов. Общие технические требования к биогазовым установкам. М.: Стандартинформ, 2019. 10 с.

2. Садчиков А.В., Кокарев Н.Ф. Оптимизация теплового режима в биогазовых установках // Фундаментальные исследования. 2016. № 2–1. С. 90-93.

3. Системы подогрева сырья в биогазовых установках. [Электронный ресурс]. URL: https://www.rosbiogas.ru/literatura/rukovodstvo-po-biogazovim-texnologiyam/sistemi-podogreva-sirya-v-biogazovix-ustanovkax.html (дата обращения: 14.12.2022).

4. Лымбина Л.Е. Математическое моделирование динамических процессов в стенке при ступенчатом изменении теплового потока // Современные научные достижения металлургической теплотехники и их реализация в промышленности: сборник докладов международной научно-практической конференции, посвященной 95-летию основания кафедры ТИМ, УрФУ и 85-летию основания ОАО «ВНИИМТ» (Екатеринбург, 17–18 сентября 2015 г.). Екатеринбург: УрФУ, 2015. С. 387–395.

5. Орлов М.Е. Теоретические основы теплотехники. Тепломассообмен: учебное пособие. Ульяновск: УлГТУ, 2013. 204 с.

6. Номер биота. [Электронный ресурс]. URL: http://ru.knowledgr.com (дата обращения: 14.12.2022).

7. Гутова С.Г., Каган Е.С. Моделирование систем автоматического регулирования: учебное пособие. Кемерово: КемГУ, 2020. 230 с.

8.. Бухмиров В.В., Ракутина Д.В. Справочные материалы для решения задач по курсу «Тепломассообмен». Иваново: ФГБОУ ВО «Ивановский государственный энергетический университет им. В.И. Ленина», 2017. 120 с.

Важная роль в современном развитии энергетической отрасли России принадлежит биоэнергетике, основой которой является использование различных биоматериалов в качестве топлива. Обусловлено это многими факторами, среди которых истощение ископаемых энергоресурсов, а также возможность с помощью биоэнергетики решить экологические проблемы. Биогазовые установки (БГУ) обеспечивают переработку органических отходов (стоков животноводческих производств и растениеводства) и осадков сточных вод в биогаз (горючий газ). Попутно с биогазом на БГУ получают высокоэффективное дорогостоящее жидкое органическое удобрение [1].

Для достижения максимальной эффективности образования биогаза и получения органических удобрений в БГУ должен поддерживаться оптимальный для данной установки температурный режим – важнейший фактор процесса сбраживания [2]. Для обеспечения оптимального температурного режима, а также для лучшего обеззараживания сырья, используются два метода подогрева: прямой подогрев в форме пара или смешивающейся с сырьем горячей воды и непрямой подогрев через теплообменные устройства с различными нагревательными устройствами [3]. Добавление горячей воды повышает влажность субстрата и поэтому может использоваться только там, где это допустимо. Внешний подогрев с помощью теплообменника с теплопроводящими элементами на поверхности стен реактора биогазовой установки менее эффективен из-за потерь тепла с поверхности стен. Непрямой подогрев с размещением теплообменных устройств в зоне действия перемешивающего устройства помогает избежать осаждения твердых частиц на их поверхности. В современных мощных электронагревательных приборах в качестве основы их нагревательных устройств используются трубчатые электрические нагреватели – ТЭНы.

Таким образом, одной из важных и актуальных задач повышения эффективности работы БГУ является задача оптимального поддержания температурного режима в условиях определенной системы подогрева. Достижение желаемого эффекта невозможно без совершенствования систем управления тепловыми процессами как на этапе загрузки среды в биореакторы (метантенки) БГУ, так и в режиме стабилизации. Эта задача требует разработки и реализации математической модели, учитывающей влияние тепловых потоков на температуру среды в процессе анаэробного сбраживания в биореакторе.

Целью исследования является анализ инерционности нагревателя на основе формализации полученной его математической модели с учетом процесса переноса тепла через стенку и предварительно рассчитанных областей значений чисел массивности и значений постоянной времени при конвективном механизме теплоотдачи.

Материалы и методы исследования

Тепловые потоки свойственны теплообменным агрегатам как периодического, так и непрерывного действия. Функционирование теплообменного агрегата метантенка БГУ проходит в нестационарном тепловом режиме, который характеризуется предварительным нагревом сырья заданного объема и в течение определенного времени перед загрузкой в биореактор и режимом стабилизации температуры среды в биореакторе с высокой точностью, особенно для термофильного режима сбраживания. Решение такой задачи требует получения модели по каналу изменения температуры с учетом динамики тепловых потоков, создающих возмущение на температуру среды через поверхность стенки нагревателя. Возмущение от теплового потока нагревателя влияет на температуру среды в аппарате через стенку нагревателя. Теплопередающая поверхность нагревателя изготавливается из различных материалов, теплофизические свойства которых также изменяются при изменении температуры.

В работе [4] получены основные уравнения переноса тепла через стенку с применением классического метода решения задачи теплофизики – метода Фурье при граничных условиях для случая конвективного механизма теплоотдачи с помощью учета в уравнениях констант – критериев Био, характеризующих неравномерность температурного поля, и критерия Фурье, характеризующего нестационарность процессов [5].

В данной работе с учетом сложных теплофизических эффектов и полученных в [4] основных уравнений теплопереноса через стенку в динамическом режиме формализована математическая модель процесса нагрева среды по каналу возмущения от теплового потока нагревателя (трубчатого электронагревателя, например ТЭНа, теплообменника и др.) для целей моделирования системы управления тепловым агрегатом – метантенком БГУ. Оценка инерционности теплового объекта проведена путем анализа передаточной функции процесса при ступенчатом изменении теплового потока в стенке нагревателя для практического использования этой информации при математическом моделировании динамических процессов в трубчатом электронагревателе.

При конвективном механизме теплоотдачи коэффициентами модели являются коэффициент теплопроводности изотропного материала стенки, полная толщина стенки, а также коэффициенты теплоотдачи конвекцией в стационарном режиме со стороны рабочей среды (α1) и со стороны окружающего пространства (α2). Учет влияния излучения производится суммированием коэффициентов теплоотдачи – конвективного и лучистого. При конвективном механизме теплоотдачи числа массивности стенки æ1 и æ2 , входящие как константы в динамические уравнения, являются числами Био [4]: æ1 = Вi1 = α1 ∙ Δх/λ, æ2 = Вi2 = α2 ∙ Δх/λ, где ∆x – толщина стенки; λ – коэффициент теплопроводности изотропного материала стенки; α1, α2 – коэффициенты теплоотдачи конвекцией в стационарном режиме со стороны рабочей среды и со стороны окружающей среды. Теплопередающие поверхности нагревателей изготавливаются из различных материалов, теплофизические свойства которых также изменяются с изменением температуры. Если представить изменения коэффициентов теплоотдачи от естественной конвекции до конвекции при фазовых переходах в интервале α1 = 10…2∙103 Вт/м∙К, а изменение теплопроводности материалов нагревателя – в интервале λ = 0,01… 400 Вт/м∙К, то область значений числа æ1 при изменении ее толщины Δх = 0,005…0,1 м составляет æ1 = 5 … 0,0025 (при α1 = 10 Вт/м∙К) и æ1 = 1000 … 0,5 (при α1 = 2000 Вт/м∙К). При тех же данных и при изменении коэффициента теплоотдачи α2 в 10 … 400 Вт/м∙К область значений æ2 составляет æ2 = 5 … 0,0025 (при α2 = 10 Вт/м∙К) и æ2 = 200 … 0,1 (при α2 = 400 Вт/м∙К).

Результаты исследования и их обсуждение

В табл. 1, 2 приведены расчетные значения параметров æ1 и æ2 в зависимости от α1 и α2 для различных значений ∆x и λ. При анализе полученных значений следует учитывать, что значения числа Био меньше 0,1 означают, что теплопроводность внутри стенки намного быстрее, чем конвекция тепла вдали от его поверхности, а градиенты температуры незначительны внутри него. Это может указывать на применимость (или неприменимость) в решении данной задачи методов анализа сосредоточенных систем) [6]. Обычно этот метод анализа приводит к простому экспоненциальному нагреванию, поскольку количество тепловой энергии (в широком смысле количество «тепла») в теле прямо пропорционально его температуре, которая, в свою очередь, определяет скорость передачи тепла в него или из него. Это приводит к простому дифференциальному уравнению первого порядка, описывающему теплопередачу в этих системах, что подтверждено полученной моделью в данной работе.

Таблица 1

Значение параметра æ1 в зависимости от α1 при Δх = 0,005; 0,1; λ = 0,01… 400

Таблица 2

Значение параметра æ2 в зависимости от α2 при Δх = 0,005; 0,1; λ = 0,01 … 400

В общем случае влияние изменяющейся температуры стенки на тепловой поток описано в работе [4] передаточной функцией, содержащей сумму бесконечного ряда, следующего вида:

W*(p) = k / (1 + a1 р + a2 р2 + … ) = k / (1+aj ∙ рj), j =1, 2 … . (1)

где k = æ2 / (æ1 + æ2 + æ1 ∙ æ2) – коэффициент передачи;

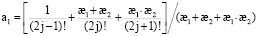, j =1, 2 … .

Ограничившись в выражении (1) первыми членами (приняв j = 1), как правило, наиболее существенными в сумме, получим модель влияния теплового потока на температуру стенки в виде передаточной функции апериодического звена первого порядка:

W(p) = k / (1+ Т∙р), (2)

где T = α1 ∙ Ts – постоянная времени, определяемая соотношениями

;

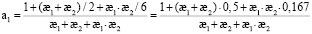Ts = α1 ∙ ρ ∙ c ∙ (Δх)2 / λ; λ – коэффициент теплопроводности; ρ – плотность; с – удельная массовая теплоемкость.

Это приближение мало отличается от параметров переходных характеристик, рассчитанных с помощью сумм бесконечных рядов. Передаточная функция (2) соответствует процессу переноса тепла в динамическом режиме в области изображений по Лапласу относительно безразмерного времени, т.е. числа Фурье Fo = λ∙τ/ρ∙c (∆x)2. Для получения передаточной функции в области изображений относительно размерного времени τ был заменен аргумент-оператор р на Ts∙p, где Ts – постоянная времени, определяемая соотношением Ts=ρ∙c∙(∆x)2/λ. Эта замена без сложных преобразований объясняется тем, что в определении изображений по Лапласу функции комплексного переменного F(p)=∫f(τ)∙e-pτ dτ независимые постоянные ∆x и λ/ρ∙c выносятся за знак интеграла [7].

Физические характеристики λ, ρ, c функционально связаны с коэффициентом температуропроводности, характеризующим темп нагрева тела, соотношением а = λ /ρ∙c [8]. Коэффициент температуропроводности для стальной стенки можно охарактеризовать значением а ≈ 10-5 м2/с. В нашем случае при расчете Тs используется величина, обратная коэффициенту а (1/а=ρ∙c/λ), являющаяся тепловой инерцией. С учетом значений а и тепловой инерции, равной 105, постоянная времени равна Т = а1∙а∙(∆x)2 = а1 ∙(∆x)2∙105.

Для адаптации полученной модели в качестве аппроксимирующей функции инерционности объекта, например, ТЭНа при ступенчатом изменении теплового потока необходимо рассмотреть конкретные значения постоянной времени, характеризующей динамику изменения температуры в стенке нагревателя при изменении условий теплопереноса. Так, для условий стальной стенки и различных значений коэффициента теплопроводности и коэффициентов æ1 = 0,01 и æ2 в интервале 0,01 … 10,0; æ2 = 0,1 и æ1 в интервале 0,01 … 10,0 при изменении Δх от 0,005 до 0,1 м с использованием рассчитанных в табл. 3 с учетом тепловой инерции, равной 105, значений параметра а1 получены значения постоянной времени Т , приведенные в табл. 4.

Таблица 3

Значения параметра а1 в функции чисел массивности æ1, æ2

Таблица 4

Значения параметра Tq в функции толщины стенки ∆x, а1 при æ1 и æ2, равных 1; 2,5; 5; 7,5; 10,0

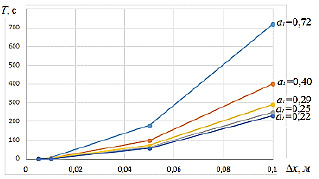
Рис. 1. Зависимость постоянной времени нагревателя в функции толщины стенки Δх при æ1 = æ2 =1,0 … 10

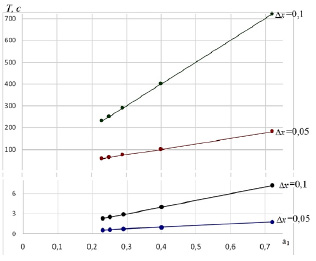
Рис. 2. Зависимость постоянной времени нагревателя в функции параметра а1, характеризующего условия теплоотдачи при конвективном механизме

Используя предварительно рассчитанные области значений чисел æ1 и æ2, в табл. 4 приведены расчетные значения постоянной времени нагревателя при конвективном механизме теплоотдачи.

На рис. 1 представлены зависимости изменения постоянной времени Т в функции характерного линейного размера стенки Δх при значениях чисел массивности стенки æ1 и æ2 = 1,0 … 10,0, определяющих значения параметра а1 от 0,22 до 0,72 при конвективном механизме теплоотдачи. Заметно сильное влияние на Т больших значений Δх. При фиксированной толщине стенки Δх постоянная времени Т, как видно из рис. 2, линейно связана с изменениями параметра а1, характеризующего условия теплоотдачи при конвективном механизме.

Заключение

Изменение плотности теплового потока со стороны рабочей или внешней среды следует рассматривать как возмущение теплового потока на объект управления, например на трубчатый теплоэлектронагреватель. Со стороны внешней среды могут происходить изменения, связанные, например, с изменением скорости движения биомассы в биореакторе в результате перемешивания, отражающиеся на величине теплового потока. В этих условиях влияния тепловых потоков со стороны рабочей и внешней среды отражаются на изменении температуры стенки. Используя математическую модель теплопереноса через стенку нагревателя, можно получить значения постоянной времени звена, характеризующего инерционность объекта по каналу регулирования температуры в биореакторе. Зная свойства материала стенки, можно оценить рациональную толщину Δх, обеспечивающую минимальное запаздывание при фиксированной интенсивности нагрева среды. В случае фиксированной Δх можно выбрать тип нагревателя, изготовленного из материала, обладающего определенными (требуемыми) теплофизическими свойствами и предельной температурой.

Полученные результаты могут быть использованы при разработке системы регулирования температуры с помощью теплового потока нагревателя, различного для режима предварительного нагрева сырья и для режима стабилизации температуры. Для исключения перегрева рекомендуется многопозиционное регулирование, момент переключения при котором должен быть определен с учетом инерционности и запаздывания. Последнее можно определить с использованием рассчитанных численных данных по методике, представленной в данной работе.

Библиографическая ссылка