Повышенный интерес компаний к освоению месторождений полезных ископаемых, находящихся за полярным кругом, связан с тем, что, по прогнозам ученых, на шельфе Северного Ледовитого океана сосредоточено более 20 % мировых запасов нефти и газа [1]. Для организации эффективной добычи и транспортировки углеводородов компании используют автоматизированные системы дистанционного мониторинга, контроля и управления (АСДМКУ). При этом для организации постоянного и достоверного обмена данными между оперативным центром и необслуживаемыми объектами управления (НОУ) используются низкоорбитальные системы спутниковой связи (НССС), имеющие в своем составе не менее 40 космических аппаратов (КА). По мере освоения месторождений будет увеличиваться число группировок НССС. В результате этого в зону видимости приемника, расположенного на НОУ, могут попасть сразу несколько КА. В этом случае спутник-нарушитель получит возможность навязать ретрансляционную помеху, которая представляет собой переданную ранее команду управления. Предотвратить такое деструктивное воздействие возможно путем повышения имитостойкости НССС за счет использования системы опознавания КА.
В основе работы систем опознавания КА предлагается использовать протоколы аутентификации с нулевым разглашением знаний [2]. Так как данные методы аутентификации используют большие простые числа, то они имеют недостаток – значительные временные затраты на опознавание. При этом чем больше времени на опознавание КА, тем больше вероятность того, что нарушитель сможет подобрать правильный сигнал ответчика. Сократить время вычисления за счет уменьшения разрядности простых чисел нельзя, так как это снижает стойкость протокола аутентификации. Решить эту проблему можно за счет применения кодов полиномиальной системы классов вычетов (ПСКВ). Цель статьи – сократить время опознавания КА за счет ПСКВ, так как в этих кодах вычисления осуществляются с остатками и производятся параллельно и независимо по основаниям.
Материалы и методы исследования
При построении системы опознавания, которая состоит из запросчика и ответчика, часто применяются методы аутентификации, использующие системы шифрования. Данные системы позволяют обеспечить высокую криптостойкость запросно-ответной системы к подбору правильного сигнала ответчика. При этом, как правило, используются симметричные системы шифрования. В этом случае сигнал запросчика (З) MЗ представляет собой зашифрованное с помощью секретного ключа К случайное число RЗ. Ответчик расшифровывает сигнал запросчика и получает число RЗ. Затем он, используя секретный ключ К, генерирует зашифрованный сигнал ответчика (О) МО, который поступает запросчику. Последний расшифровывает его и получает RЗ – 1. Данный процесс опознавания можно представить в виде
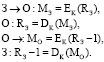(1)
Выбор симметричных систем шифрования для выполнения протокола (1) определяется тем, что они обеспечивают минимальные временные затраты на аутентификацию. В работе [3] показано, что максимальная скорость симметричного шифрования в системе на кристалле ATL186 достигает значения 400 Мбит/с. Однако при использовании симметричных шифров в системах опознавания возникает проблема, связанная с доставкой секретных ключей запросчику и ответчику. Особенно она актуальна для систем опознавания космических аппаратов, которые несколько лет находятся на орбите. Если в процессе передачи запросчику или ответчику злоумышленник сможет перехватить секретный ключ, то он легко подделает сигнал ответчика. В результате этого снизится имитостойкость НССС и спутник-нарушитель получит доступ к каналу связи.
Обеспечить высокую имитостойкость НССС позволяют методы аутентификации, которые используют протоколы с нулевым разглашением знаний. Данные протоколы имеют высокую вычислительную сложность, благодаря которой обеспечивается низкая вероятность подбора правильного ответа без использования шифрования [4]. Первыми протоколами аутентификации были протоколы Фиат – Шамира и Фейге – Фиат – Шамира. Для обеспечения высокой криптостойкости для протокола Фиат – Шамира надо было реализовать от 20 до 40 раундов вычислений, а для протокола Фейге – Фиат – Шамира – от 4 до 8 раундов. Для снижения временных затрат на аутентификацию были разработаны протоколы Шнорра, Гиллу – Кискатра. Дальнейшее снижение времени на аутентификацию обеспечил протокол, приведенный в работе [5]. Данный результат был достигнут за счет уменьшения числа операций на этапе аутентификации претендента.
Несмотря на то, что данные протоколы имеют только один раунд аутентификации, она не обеспечивают максимальную скорость аутентификации, так как все вычисления производятся по большому модулю. Для снижения временных затрат на выполнение аутентификации в работе [6] предложено использовать коды системы остаточных классов вычетов (СОК). В данных кодах вычисления производятся по основаниям, в качестве которых использовались простые числа.
Дальнейшее повышение имитостойкости НССС возможно за счет применения кодов ПСКВ, которые, обладая скоростью проводимых вычислений, сравнимой с кодами СОК, способны генерировать большее количества ответных сигналов благодаря использованию многочленов, имеющих одинаковую степень. В этих кодах ПСКВ целые числа представляются в полиномиальной форме. Затем полученные полиномы делятся на неприводимые многочлены mi (x), где i = 1, 2, … n, которые являются основаниями ПСКВ. В результате получается кортеж остатков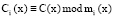 
, где i = 1, 2, … n
,
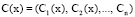Принципы построения и выполнение модульных операций в кодах ПСКВ приведены в работе [7]. Для модульных операций справедливо
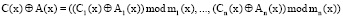, (2)
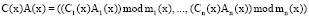, (3)
где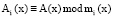 
; i = 1, 2, … n.
Количество разрешенных комбинаций кода ПСКВ задается рабочим диапазоном
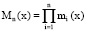. (4)
Проведем модификацию метода аутентификации КА, представленного в [4]. Набор оснований осуществляется так, чтобы выполнялось условие
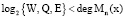, (5)
где W – секретный ключ КА; Q – случайное число; Е – случайное число.
Число Q позволяет генерировать сеансовый ключ Q(j), где j – номер сеанса. Так как в процессе генерации Q(j) может произойти сбой, то операционный центр должен определить повторное использование Q(j). Для этого используется случайное число Е, используемое для генерации параметра Е(j), с помощью которого можно проверить повторное применение Q(j). В качестве порождающего элемента выбираем е(х) = х.
Предварительный этап протокола аутентификации в ПСКВ.
1. Ответчик вычисляет секретные параметры для j-го сеанса, где j = 1, 2, ….
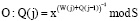, (6)
где S – большое простое число;
.
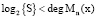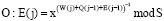. (7)
2. Ответчик представляет секретные параметры в виде кода ПСКВ
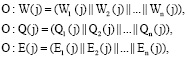(8)
где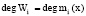 
; 
;
.
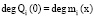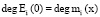3. Ответчик вычисляет «истинный» статус КА для j-го сеанса
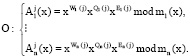.(9)
4. Ответчик искажает секретные параметры с помощью случайных чисел таких, что
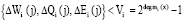. (10)
Тогда «искаженные» параметры спутника имеют вид
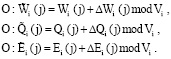(11)
5. Ответчик вычисляет «искаженный» статус КА для j-го сеанса:
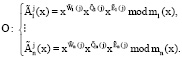(12)
Процесс аутентификации космического аппарата.
1. Запросчик передает случайное число В < S, представив его в коде ПСКВ
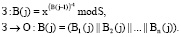(13)
2. Ответчик, получив сигнал запросчика, выполняет выражения
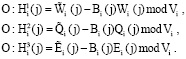(14)
3. Ответчик передает свой сигнал запросчику
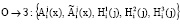. (15)
4. Запросчик получает сигнал ответчика и проверяет его
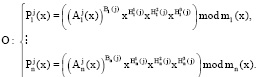(16)
6. Запросчик принимает решение «спутник свой», если выполняется
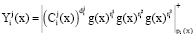. (17)
Спутнику присвоят статус «свой», если справедливо
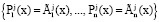. (18)
Результаты исследования и их обсуждение
Выбираем секретные параметры из условия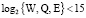 
бит. Тогда ПСКВ содержит 
, 
, 
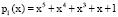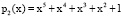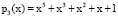Рабочий диапазон 
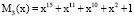. Ответчик получил секретные параметры в ПСКВ:
.
.
.
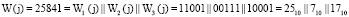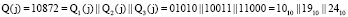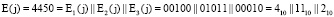Ответчик вычисляет «истинный» статус КА для j-го сеанса
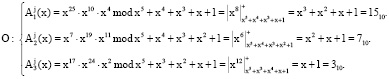
Ответчик искажает секретные параметры с помощью случайных чисел таких, что
.
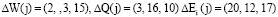Тогда «искаженные» параметры спутник имеют вид
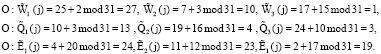
Ответчик вычисляет «искаженный» статус КА для j-го сеанса
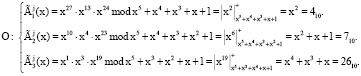
Процесс аутентификации КА. Запросчик передает ответчику случайное число
З → О: B(j) = B1(j) || B2(j) || B3(j) = 00101 || 01010 || 00111 = 5 || 10 || 7.
Ответчик, получив сигнал запросчика, выполняет выражения
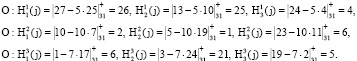
Ответчик передает сигнал О → З: {(15, 7, 3)(4, 7, 26)(26, 25, 4)(2, 1, 6)(6, 21, 5)}.
Запросчик, получает сигнал ответчика и проверяет его
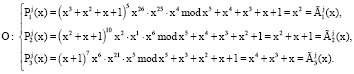
Запросчик принимает решение «спутник свой» и предоставляет сеанс связи.
На основе модифицированного метода аутентификации была разработана структурная модель системы опознавания КА, которая была реализована на FPGA Xilinx Artix-7 (xc7s6ftgb196-1). Тестирование велось на платформе Vivado HLS 2019.1. Для одномодульного метода аутентификации выбрано S = 11337409. В модифицированном методе были использованы пять полиномов пятой степени. Операции возведения в степень по модулю были выполнены с помощью алгоритма Монтгомери. Исследования показали, что при использовании одномодульного протокола аутентификации для опознавания спутника необходимо To = 5936 нс. В данном показателе представлено время на получение истинного и «искаженного» статуса КА, вычисление ответов на вопрос запросчика и проведение проверки этих ответов. Временные затраты на получение параметров Q(j), E(j) и вопроса запросчика B(j) не учитывались. Исследование модифицированного метода аутентификации на основе ПСКВ показало, что временные затраты на опознавание равны TПСКВ = 3238 нс. Таким образом, использование кодов ПСКВ позволило сократить время опознавания спутника в 1,83 раза за счет выполнения параллельных вычислений с малоразрядными операндами. Таким образом, сокращение времени опознавания КА повысит имитостойкость НССС за счет уменьшения вероятности подбора злоумышленником правильного сигнала ответчика.
Заключение
В статье проведена модификация метода аутентификации для низкоорбитальных спутников на основе кодов ПСКВ. Использование данных кодов сокращает временные затраты на опознавание КА за счет параллельного выполнения вычислений с малоразрядными остатками. Для оценки эффективности модифицированного метода аутентификации была разработана структурная модель системы опознавания КА, которая была реализована на FPGA Xilinx Artix-7. Исследования показали, что при использовании одномодульного метода аутентификации для опознавания КА потребуется To = 5936 нс, а при использовании модифицированного метода – TПСКВ = 3238 нс. Таким образом, использование кодов ПСКВ позволило сократить время опознавания спутника в 1,83 раза за счет выполнения параллельных вычислений с малоразрядными операндами.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-37-90009.
Библиографическая ссылка
Чистоусов Н.К., Калмыков И.А., Духовный Д.В., Калмыкова Н.И., Емельянов Е.А. МОДИФИКАЦИЯ МЕТОДА АУТЕНТИФИКАЦИИ НИЗКООРБИТАЛЬНЫХ СПУТНИКОВ НА ОСНОВЕ КОДОВ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ // Современные наукоемкие технологии. – 2022. – № 2. – С. 164-169;URL: https://top-technologies.ru/ru/article/view?id=39052 (дата обращения: 24.11.2024).