Определение изоморфизма графов на основе инвариантов – один из эффективных подходов к распознаванию объектов различной природы. Показано экспериментально, что при определении изоморфизма графов с малым числом вершин высокую эффективность имеет вектор степеней вершин, но в случае восьми вершин и более неизоморфные графы могут иметь идентичные векторы [1]. Достаточно эффективным оказался вектор собственных чисел матрицы смежности графа, что позволяет вычислять изоморфизм некоторых графов за полиномиальное время. Отмечается, что вектор степеней вершин и характеристики, извлекаемые из матриц смежности, несомненно, являются полезными инвариантами, но не решают в общем случае задачу изоморфизма. В работе [2] в качестве инвариантов предлагается использовать объединения локальных характеристик графа, например плотность, хроматическое число, число Хадвигера, индексы Виннера и Рандича. Менее эффективны следующие инварианты: определитель матрицы смежности, число компонент связности и диаметр графа. Алгоритм вычисления полного инварианта графа изложен в работе [3]. Предложена система кодирования, которая обеспечивает получение интегрального описателя структуры, инвариантного относительно исходной нумерации её вершин.
Работа направлена на поиск новых инвариантных характеристик, получаемых в результате целенаправленного преобразования графа эвристическим алгоритмом за полиномиальное время. Важно отметить, что проблема распознавания изоморфизма за полиномиальное время является одной из нерешенных проблем современной теории сложности вычислений. Поэтому эффективными являются исследования, опирающиеся на эвристику. Сочетание точных алгоритмов и эвристических, основанных на итерационном уточнении решений, рассмотрено, например, в работе [4]. В статье [5] представлена эвристика для решения проблемы изоморфизма графов методами вероятностного линейного программирования. В настоящей работе выполнены исследования в рамках поиска устойчивых эвристических характеристик, способствующих выявлению изоморфизма.
Материалы и методы исследования
В настоящей работе в качестве исходного материала для решения задачи изоморфизма рассматриваются простые связные графы. Пусть исходные данные представлены в виде графа G = (V, E), где V – множество вершин; E – множество ребер, содержащего n вершин и m ребер.
В качестве метода исследования выступает проверка гипотезы о положительных инвариантных свойствах кортежа графа, характеризуемого минимумом суммарной длины всех связей в кортеже, а в качестве атрибута для определения изоморфизма, – собственно упорядоченный вектор длин, приписываемых вершинам кортежа. Для оценки качества кортежа вводится понятие длины ребра как неотрицательной разности порядковых номеров вершин в кортеже, инцидентных данному ребру. С учетом этого суммарная длина ребер полного графа равна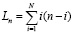 
, где 
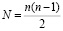есть число ребер графа. Таким образом, к матрице смежности, задающей граф с помеченными вершинами, вектору степеней вершин и другим его инвариантам добавляются новые полезные элементы [6].
Дадим некоторые определения.
Функцию f, относящую каждому графу G некоторый элемент f(G) из множества M, будем называть инвариантом, если на изоморфных графах ее значения совпадают, т.е. для любых G и Gʹ: G ≅ Gʹ ⇒ f(G) = f(Gʹ).
Инвариант графа, удовлетворяющий необходимому и достаточному условию изоморфизма, т.е. G ≅ Gʹ ⇔ f(G) = f(Gʹ), будем называть полным. Если на сравниваемых графах значения функции f отличаются на допустимые величины Δ, т.е. для любых L и Lʹ G ≅ Gʹ ⇒ │f(G) – f(Gʹ)│ ≤ Δ, то будем называть ее субинвариантом. Такой подход обеспечивает возможность приближенного сравнения графовых моделей с допустимой погрешностью.
Для получения новых элементов, дополняющих вектор инвариантов, рассмотрим эвристический метод построения кортежа графа с требуемыми свойствами. Суть метода состоит в формировании кортежа вершин графа G, в котором вершины с большим числом связей между собой размещаются в кортеже по соседству, а слабо связанные вершины – в отдаленных друг от друга позициях. Алгоритм, приведенный в работе [7], позволяет в цикле строить кортеж графа G с минимальной суммарной длиной ребер. Количество глобальных циклов n определяется числом вершин в графе. Алгоритм в каждом цикле (шаге) с номером r оперирует двумя подграфам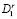и 
и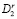 
графа G = (V, E) с выбранными и еще не выбранными вершинами графа соответственно. На каждом r цикле выбирается и отмечается индексом r одна из неотмеченных вершин 
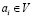подграфа 
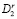, связанная непосредственно с одной или несколькими вершинами подграфа 
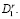Эта вершина переносится из подграфа 
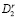в граф 
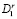и служит очередной вершиной формируемого кортежа. При выборе r-й компоненты картежа на r-м цикле алгоритма отыскивается такая вершина 
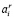, для которой 
– 
= 
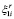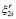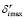, где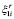 
– число дуг, связывающих вершину ai с 
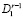а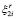 
– число дуг, связывающих ai с 
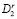. Каждый цикл связан с анализом и оценкой n – r еще не выбранных вершин-кандидатов. Таким образом, в итоге получаем искомый кортеж с минимизированной суммарной длиной связей и соответствующую ему матрицу смежности. Вычислительную сложность алгоритма построения кортежа можно оценить как n(n – 1).
Результаты исследования и их обсуждение
Пусть заданы два графа G1 = (V1, E1) и G2 = (V2, E2), причем второй получен путем переименования вершин.
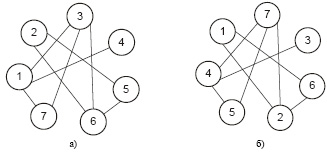
Рис. 1. Графы G1 (a) и G2 (б)
Таблица 1
Исходная матрица смежности графа G1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
1 |
1 |
1 |
1 |
|||
|
2 |
1 |
1 |
1 |
||||
|
3 |
1 |
1 |
1 |
1 |
|||
|
4 |
1 |
1 |
|||||
|
5 |
1 |
1 |
1 |
||||
|
6 |
1 |
1 |
1 |
1 |
|||
|
7 |
1 |
1 |
1 |
Матрица смежности графа G1 приведена в табл. 1. Заметим, что в этой и последующих матрицах смежности в диагоналях для элементов с одинаковыми индексами содержатся «1», которые не означают наличия петель в графах, а служат исключительно для визуального анализа распределения единиц вокруг диагоналей. Кортеж, построенный по данной матрице смежности, имеет вид, представленный на рис. 2, а. Суммарные длины ребер в кортеже в соответствии с их номерами (11, 7, 9, 3, 4, 8, 10). Общая длина восьми ребер без повторений L1 = 26. Применяя алгоритм построения кортежа с минимальной суммарной длиной ребер, получим результат, приведенный на рис. 2, б.
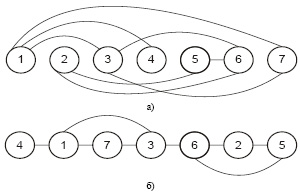
Рис. 2. Кортеж графа G1 без оптимизации (а) и с минимальной суммарной длиной ребер (б)
Суммарные длины ребер при вершинах графа в оптимизированном кортеже в соответствии с их порядковыми номерами в кортеже (1, 4, 2, 4, 4, 2, 3). Общая длина ребер без повторений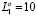 
. Матрица смежности графа G1 после упорядочения представлена в табл. 2.
Видно, что единицы группируются вдоль главной диагонали. Рассмотрим для сравнения и определения возможного изоморфизма граф G2 = (V2, E2) с другой разметкой вершин (табл. 3).
Результаты его отображения в виде кортежа и упорядоченного кортежа в соответствии с алгоритмом, представлены на рис. 3, а и б.
В табл. 4 приведена преобразованная в соответствии с алгоритмом построения оптимизированного кортежа матрица смежности графа G2.
Таблица 2
Преобразованная матрица смежности графа G1
|
4 |
1 |
7 |
3 |
6 |
2 |
5 |
|
|
4 |
1 |
1 |
|||||
|
1 |
1 |
1 |
1 |
1 |
|||
|
7 |
1 |
1 |
1 |
||||
|
3 |
1 |
1 |
1 |
1 |
|||
|
6 |
1 |
1 |
1 |
1 |
|||
|
2 |
1 |
1 |
1 |
||||
|
5 |
1 |
1 |
1 |
Таблица 3
Исходная матрица смежности графа G2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
1 |
1 |
1 |
||||
|
2 |
1 |
1 |
1 |
1 |
|||
|
3 |
1 |
1 |
|||||
|
4 |
1 |
1 |
1 |
1 |
|||
|
5 |
1 |
1 |
1 |
||||
|
6 |
1 |
1 |
1 |
||||
|
7 |
1 |
1 |
1 |
1 |
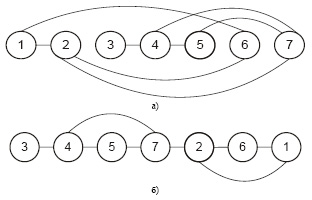
Рис. 3. Кортеж графа G2 без оптимизации (а) и с минимальной суммарной длиной ребер (б)
Таблица 4
Преобразованная матрица смежности графа G2
|
3 |
4 |
5 |
7 |
2 |
6 |
1 |
|
|
3 |
1 |
1 |
|||||
|
4 |
1 |
1 |
1 |
1 |
|||
|
5 |
1 |
1 |
1 |
||||
|
7 |
1 |
1 |
1 |
1 |
|||
|
2 |
1 |
1 |
1 |
1 |
|||
|
6 |
1 |
1 |
1 |
||||
|
1 |
1 |
1 |
1 |
Длины ребер при вершинах в кортеже (рис. 3, а) в соответствии с их номерами представлены вектором (6, 10, 1, 5, 3, 9, 10). Общая длина L2 восьми ребер без повторений L2 = 22. Применяя алгоритм построения кортежа, получим граф, представленный на рис. 3, б. Суммарные длины ребер при вершинах графа в оптимизированном кортеже в соответствии с их порядковыми номерами: в кортеже (1, 4, 2, 4, 4, 2, 3). Общая длина ребер в нем без повторений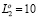 
.
Таким образом, в рассмотренном примере графы G1 и G2 в оптимизированных кортежах имеют одинаковые векторы длин ребер (1, 4, 2, 4, 4, 2, 3) и равные показатели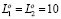 
, что в интеграции с другими инвариантами позволяет считать их изоморфными.
Отметим отдельно, что применяемый алгоритм построения кортежа [7] допускает в общем случае наличие нескольких альтернативных вариантов. Поэтому в сочетании с эвристикой может потребоваться ограниченный перебор порядка вершин с целью достижения равенства характеристик оптимизированных кортежей для G1 и G2.
Заключение
В настоящей работе предложено для определения изоморфизма воспользоваться дополнительно эвристическим алгоритмом построения кортежа графа, обладающего свойством минимума суммарной длины ребер по установленной метрике. На примере показано, что переименование вершин в графе G1 = (V1, E1) и его преобразование к графу G2 = (V2, E2) не приводит к изменению величин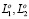 
и векторов длин ребер при вершинах оптимизированных кортежей графов. Рассмотренный алгоритм позволяет достаточно быстро строить такие кортежи, а полученные на его основе числовые характеристики целесообразно использовать в составе векторов инвариантов для определения изоморфизма.
Работа выполнена при финансовой поддержке проекта РФФИ № 20-07-00022 А «Разработка и исследование методов распознавания образов на основе инвариантов к яркостным и геометрическим преобразованиям в системах технического зрения беспилотных летательных аппаратов».
Библиографическая ссылка
Хачумов М.В., Талалаев А.А., Хачумов В.М. ОБ ОДНОМ ЭВРИСТИЧЕСКОМ КРИТЕРИИ В ЗАДАЧЕ ОПРЕДЕЛЕНИЯ ИЗОМОРФИЗМА ГРАФОВ НА ОСНОВЕ ИНВАРИАНТОВ // Современные наукоемкие технологии. – 2022. – № 2. – С. 159-163;URL: https://top-technologies.ru/ru/article/view?id=39051 (дата обращения: 24.11.2024).