Известные методы качественной теории дифференциальных уравнений представляют собой результаты фундаментальных исследований [1, 2] преимущественно теоретического характера. В то же время они лежат в основе практически всех приложений [3, 4]. Как правило, для построения этих методов не используются средства вычислительной математики, хотя исследования в области связи численных методов с устойчивостью проводятся на системной основе [5–7]. Непосредственное использование численных методов решения обыкновенных дифференциальных уравнений (ОДУ) для построения критериев устойчивости по Ляпунову (ниже устойчивости) предпринято в [8, 9], кроме того в [10, 11], а также в [12, 13]. На этой основе удается сформулировать необходимые и достаточные условия устойчивости, которые с применением численных методов приобретают конструктивный характер, программно реализуемы и дают возможность численного моделирования устойчивости по ходу приближенного решения ОДУ [11, 12]. В данном направлении возникают самостоятельные задачи исследования, часть из них неформально заключается в следующем. Требуется выяснить, какие разновидности необходимых и достаточных условий устойчивости можно построить на основе численных методов решения ОДУ. Необходимо определить формальные ограничения, при которых они математически корректны, описать области их применения, исследовать возможность использования для численного моделирования устойчивости. Отдельно ставится задача получения формализованных оценок устойчивости на основе знаков компонентов решения и двух их производных. Построение оценок должно исходить из компонентов функции правой части дифференциальной системы и их производных, обоснование оценок должно быть связано с интегральной формой необходимых и достаточных условий устойчивости.
Цель исследования заключается в том, чтобы оценить возможное разнообразие необходимых и достаточных условий устойчивости, выяснить взаимосвязь и различие между ними, указать особенности решений и дифференциальных систем, к которым применима каждая их разновидность. Требуется представить обоснование предложенных критериев, показать их конструктивность, выполнить численный эксперимент с проверкой их достоверности, раскрыть способы и особенности компьютерной реализации.
Исходные положения. Пусть рассматривается задача Коши для системы ОДУ, которая имеет нулевое решение (точку покоя)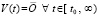 
,
, 
, 
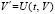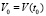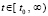, (1)
где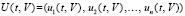 
, 
, 
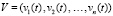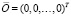. Требуется исследовать устойчивость в смысле Ляпунова точки покоя этой системы. Ниже возмущение 
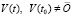, нулевого решения, если при необходимости не оговорено иное, не будет отмечаться специальным символом. Используются канонические нормы вектора, по умолчанию 
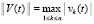. Предполагается, что существует δ0 > 0, такое, что в области 
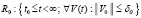, V0 = V(t0), выполнены все условия существования и единственности решения, в частности вектор-функция U(t,V) определена, непрерывна в R0 и удовлетворяет условию Липшица:
.
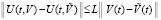
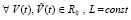Для дальнейшего потребуется более жесткое ограничение, из которого следует условие Липшица. Именно, всюду ниже предполагается, если не оговорено иное, что выполнено соотношение
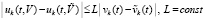
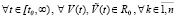. (2)
В случае, когда сравниваются нулевое решение и его возмущение, с учетом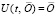 
(производная от постоянной функции 
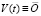равна нулю), условие Липшица примет вид
,
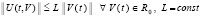а соотношение (2) перейдет в соотношение
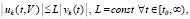
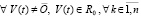. (3)
В рассматриваемых условиях точка покоя устойчива, если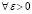 
найдется 
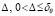, такое что 
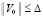влечет 
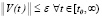. Точка покоя асимптотически устойчива, если она устойчива и найдется 
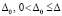, такое, что из неравенства 
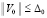следует 
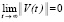. Наряду с существованием и непрерывностью 
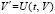ниже при необходимости предполагается существование и непрерывность в R0 второй производной 
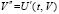, что оговаривается отдельно. Иногда будут использоваться обозначения 
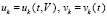. Производная каждого компонента правой части (1) аналитически определяется по формуле полной производной сложной функции [14] 
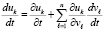, или
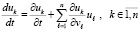. (4)
Необходимые и достаточные условия устойчивости точки покоя. В рассматриваемых предположениях, в частности включающих (2), (3), в [10, 11], а также в [12, 13] предложены следующие критерии устойчивости и асимптотической устойчивости.
Теорема 1. Для устойчивости точки покоя системы (1) необходимо и достаточно существование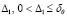 
, такого, что 
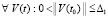выполняется соотношение
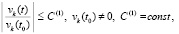
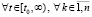. (5)
Для асимптотической устойчивости необходимо и достаточно, чтобы решение было устойчиво и существовало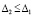 
, такое, что 
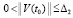влечет
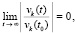
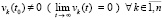. (6)
В (6) деление на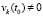 
излишне, однако так дробь вводится в компьютерную программу для исследования устойчивости, поскольку априори характер устойчивости, вообще говоря, неизвестен.
Критерии теоремы 1 в рассматриваемых условиях эквивалентны (в дальнейшем ограничения для эквивалентности будут отдельно оговорены) критериям в приводимой ниже форме.
Теорема 2. В рассматриваемых условиях, включая ограничения (2), (3), для устойчивости точки покоя системы (1) необходимо и достаточно существование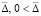 
, такого, что 
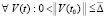выполняется соотношение
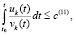
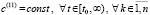. (7)
Для асимптотической устойчивости необходимо и достаточно, чтобы решение было устойчиво и существовало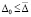 
, такое что 
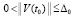влечет
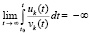
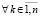. (8)
Обращение в ноль знаменателя подынтегральной функции при условии (3) приводит лишь к устранимым особенностям [12], что не влечет некорректности интегрирования (при рассматриваемых ограничениях в случае автономной системы знаменатель не обращается в ноль, поскольку различные решения не имеют общих точек [15]). Это следует из того, что левосторонний и правосторонний пределы подынтегральной функции в окрестности нуля знаменателя существуют, согласно (3) они конечны, кроме того, равны друг другу в силу непрерывности числителя и знаменателя в окрестности данной особой точки. В [11] показано, как обе приведенные теоремы вытекают из мультипликативных преобразований метода Эйлера, для целей исследования эти преобразования кратко излагаются ниже. Метод Эйлера решения задачи (1)
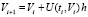, (9)
включая запись с остаточным членом, на произвольном отрезке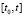 
рассматривается в предположении, что значение независимой переменной 
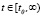является произвольно фиксированным, при этом индекс i неограниченно растет одновременно с убыванием равномерного шага:
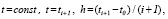
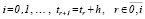. (10)
В форме с остаточным членом метод (9) примет вид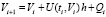 
, 
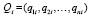, где i, h из (10), qki – остаточный член формулы Тейлора для k-го компонента приближения:
,
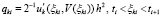аналогично, для возмущенного решения,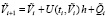 
, 
, 
, 
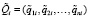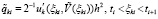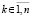. Разность между возмущенным и точным решением запишется в виде
,
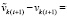
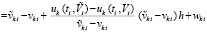
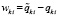или
,
,
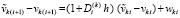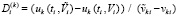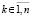. (11)
В (11) и ниже не будет учитываться случай, когда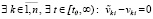 
, поскольку в предположении (2), в частности (3), эта особенность устранима и фактически не влияет на конечный результат [12]. Рекуррентное преобразование (11) влечет
,
,
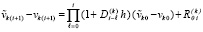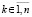, (12)
где h соответствует (10), wki из (11). В рассматриваемых условиях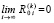 
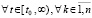[10, 11] (что равносильно сходимости метода Эйлера на произвольном отрезке 
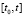). Отсюда и из (12) следует
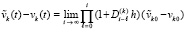
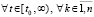. (13)
Согласно (10) предельное соотношение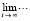 
в (13) эквивалентно 
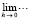, можно было бы обозначать 
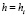, для простоты обозначений это подразумевается, но не пишется. На 
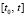частичное произведение 
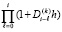при изменении i меняет одновременно все сомножители и равномерный шаг h в каждом из них. С учетом определения устойчивости из (13) непосредственно вытекает
Лемма 1. В рассматриваемых условиях для устойчивости решения задачи (1) необходимо и достаточно, чтобы существовало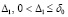 
, такое, что 
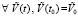, при условии 
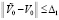выполняется неравенство
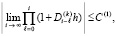
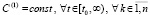. (14)
Для асимптотической устойчивости необходимо и достаточно, чтобы решение было устойчиво и существовало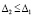 
, такое, что 
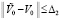влечет
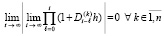. (15)
Очевидно, (13) эквивалентно соотношению
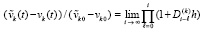
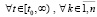. (16)
При сохранении всех рассматриваемых предположений из (16) вытекает
Следствие 1. При условии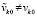 
формулировка и утверждение леммы 1 дословно сохраняются при замене (14) на соотношение
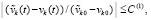
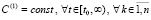, (17)
и (15) – на соотношение
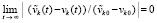
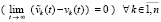. (18)
Дробь в (17) выражает отношение возмущения решения именно к вызвавшему его возмущению начальных значений при всех их вариациях в границах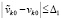 
, в этих границах выполняется соотношение
.
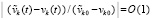
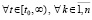Следствие 2. Следствие 1 дает необходимые и достаточные условия устойчивости точки покоя системы (1): утверждения следствия 1 сохраняются в случае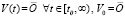 
, при этом (17) переходит в соотношение
.
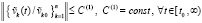Необходимые и достаточные условия асимптотической устойчивости точки покоя получаются из утверждения этого следствия с переходом (18) в соотношение
.
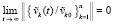
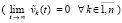Очевидно, следствие 2 эквивалентно теореме 1, которая, таким образом, вытекает из леммы 1. Данные рассуждения обратимы, и лемма 1 также следует из теоремы 1. В результате лемма 1 и теорема 1 эквивалентны в рамках рассматриваемых ограничений. В тех же ограничениях из леммы 1 следует теорема 2. В самом деле, с учетом (11) и (2) выполняется неравенство:
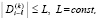
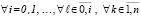. (19)
Далее, предполагается, что h достаточно мало, и на основании (19)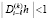 
. Тогда 
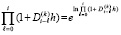, возмущение (13) преобразуется к виду
.
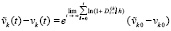
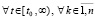Лемма 1 переходит в следующую лемму.
Лемма 2. В рассматриваемых условиях для устойчивости решения задачи (1) необходимо и достаточно существование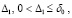 
такого, что для всех решений 
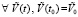, при условии 
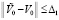выполняется соотношение
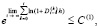
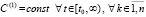. (20)
Для асимптотической устойчивости необходимо и достаточно, чтобы решение было устойчиво и существовало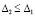 
, такое, что неравенство 
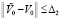влечет соотношение
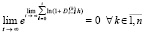. (21)
Условие (20) выполняется в том и только в том случае, если
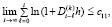
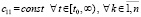, (22)
условие (21) – тогда и только тогда, когда
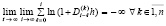. (23)
Согласно (10)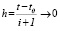 
при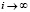 
, с учетом (19) 
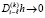, отсюда
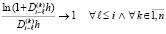. (24)
В силу (24) для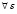 
, 
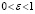, верны неравенства
.
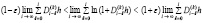При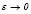 
получается аналог известного соотношения для рядов [16]:
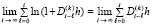
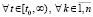. (25)
С учетом (22), (23), (25) из леммы 2 вытекает
Следствие 3. Условия, формулировка и утверждения леммы 2 дословно сохраняются при замене соотношения (20) на соотношение вида
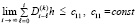
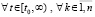, (26)
и (21) – на соотношение
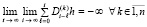. (27)
В (26), (27)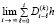 
– предел интегральной суммы на 
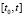, согласно (11) элементами интегрального разбиения являются дроби
,
, 
,
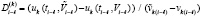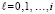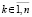представляющие собой дискретные значения функции
,
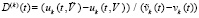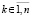. (28)
При выполнении (2) функция (28) определена и непрерывна на отрезке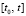 
с точностью до устранимых особенностей для каждого номера k компонента системы (1). Выражения из (26), (27) под знаком пределов включают определенные интегралы, их использование приводит к следующей теореме.
Теорема 3. В условиях леммы 2 оба утверждения этой леммы сохраняются при замене (20) на соотношение вида
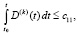
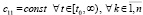, (29)
и (21) – на соотношение
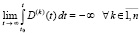, (30)
где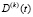 
из (28).
Числитель дроби (28) является производной возмущения, он делится на само возмущение, поэтому существует первообразная: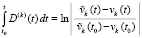 
.
Следствие 4. Теорема 3 сохраняется, если соотношения (29), (30) заменить соответственно на соотношения вида
.
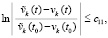
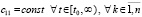и
.
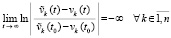где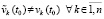 
.
В случае точки покоя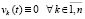 
и следствие 4 перейдет в следующее утверждение.
Следствие 5. Для случая точки покоя теорема 3 сохраняется, если соотношения (29), (30) заменить соответственно на соотношения вида
.
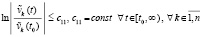и
.
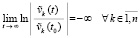где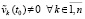 
.
Теорема 3 с учетом (28) в этом случае примет вид следующей теоремы.
Теорема 4. В условиях леммы 2 оба утверждения этой леммы сохраняются при замене (20) на соотношение вида
,
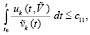
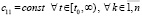и (21) – на соотношение
.
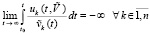Таким образом, теорема 4 вытекает из леммы 2. Данные рассуждения обратимы (с учетом предположений (2), (3), неравенства (19), а также малости h и неравенства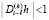 
), и эта теорема в рассматриваемых условиях эквивалентна лемме 2. Теорема 4 с точностью до обозначений повторяет теорему 2. Лемма 2 эквивалентна лемме 1. В результате теоремы 1 и 2 эквивалентны в рамках рассматриваемых ограничений.
В дальнейшем, как и в начале, возмущение точки покоя (если не оговаривается иное) не отмечается волной. В исходных обозначениях следствие 5 примет формулировку, непосредственно используемую в численном эксперименте для программной идентификации интегралов из (7), (8).
Следствие 6. Теорема 2 сохраняется, если соотношения (7), (8) заменить соответственно на соотношения вида
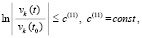
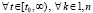(31)
и
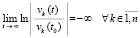, (32)
где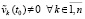 
.
Потенцирование (31), (32) влечет соответственно (5), (6).
Условия устойчивости в выражении через правую часть дифференциальной системы. Пусть предполагается существование и непрерывность в R0 второй производной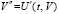 
решения системы (1). Пусть для 
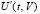имеет место аналог условия Липшица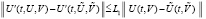 
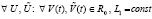, и аналог (2):
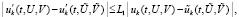
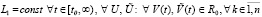. (33)
Если сравниваются производные нулевого решения и его возмущения, то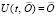 
, 
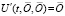, аналог условия Липшица примет вид
,
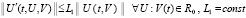а соотношение (33) перейдет в соотношение
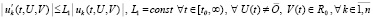. (34)
Из (34) и (3) следует неравенство
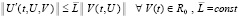. (35)
В (34), (35) и ниже на ненулевое решение и его производную не ставится знак волны. Пусть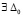 
, такое, что 
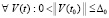обеспечивается неравенство
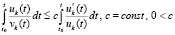
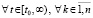. (36)
В частности, условие (36) будет выполняться, если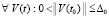 
верно соотношение
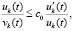
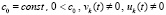
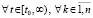. (37)
Замечание 1. По аналогии с доказательством, данным в [12] для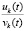 
на основе (2), (3), можно показать, что в силу выполнения (33), (34) в правых частях (36), (37) нет неустранимых особенностей.
Имеет место
Теорема 5. В рассматриваемых условиях, включающих, в частности, (33), (34), при выполнении любого из соотношений (36), (37) для устойчивости точки покоя системы (1) достаточно существования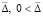 
, такого, что 
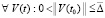выполняется соотношение
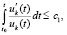
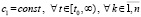. (38)
Для асимптотической устойчивости точки покоя достаточно, чтобы решение было устойчиво и существовало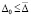 
, такое, что 
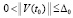влечет
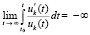
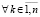. (39)
Доказательство следует из того, что при выполнении любого из условий (36), (37) соотношение (7) – необходимое следствие (38), соотношение (8) – следствие (39).
Следующая теорема эквивалентна теореме 5.
Теорема 6. В рассматриваемых условиях, включающих, в частности, (33), (34), при выполнении любого из условий (36), (37) для устойчивости точки покоя системы (1) достаточно существования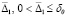 
, такого, что 
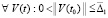выполняется соотношение
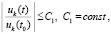
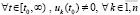. (40)
Для асимптотической устойчивости достаточно, чтобы решение было устойчиво и существовало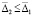 
, такое, что 
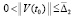влечет
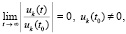
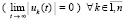. (41)
Доказательство. Неравенство (38) можно записать в виде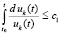 
, или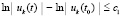 
, поэтому (38) равносильно 
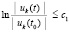, или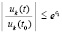 
. В итоге (38) эквивалентно (40) при 
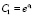. Далее, соотношение (39), 
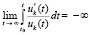, выполняется тогда и только тогда, когда выполняется 
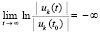. При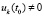 
это эквивалентно 
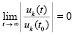, или, 
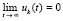. Отсюда (39) эквивалентно (41). Теорема доказана.
Из доказательства вытекает эквивалентная формулировка теоремы 5.
Следствие 7. В условиях теоремы 5 утверждения этой теоремы сохраняются, если соотношения (38), (39) заменить соответственно на соотношения
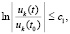
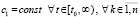. (42)
и
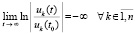. (43)
где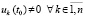 
.
Замечание 2. Для асимптотической устойчивости условие (41) необходимо без использования (36), (37), как это следует из (3). Аналогично, (39) – необходимое условие устойчивости без учета (36), (37) ввиду эквивалентности (41) и (39) (в рассматриваемых ограничениях).
Ниже даны разновидности ограничений, при наличии которых утверждения теорем 5 и 6 будут дополнены необходимыми условиями устойчивости. Пусть вначале относительно системы (1) предполагается, что в R0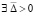 
, такое, что 
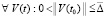выполняются пары неравенств
, 
,
, 
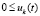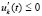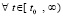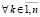, (44)
или
, 
,
, 
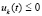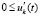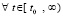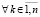. (45)
Неравенства (44) и (45) можно объединить в одно неравенство
, 
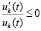
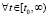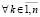, (46)
где с учетом (34) в случае нуля в знаменателе возможны лишь устранимые особенности. Пусть наряду с тем предполагается, что выполнены неравенства
,
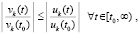
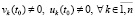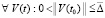. (47)
В совокупности данных предположений имеет место
Предложение 1.
Если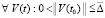 
каждый компонент правой части (1) и его производная сохраняют знак (в виде нестрогого неравенства) 
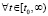, то выполнение одного из соотношений (44) или (45) необходимо, а в сочетании с выполнением (47) достаточно для устойчивости точки покоя системы (1). Для ее асимптотической устойчивости необходимо и при выполнении (47) достаточно, чтобы решение было устойчиво и существовало 
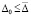, такое, что 
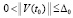влечет
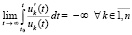. (48)
Предложение 2. Условия предыдущего предложения необходимы и при выполнении (47) достаточны для устойчивости точки покоя системы (1). В тех же условиях для ее асимптотической устойчивости необходимо и при выполнении (47) достаточно, чтобы
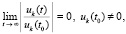
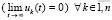. (49)
Доказательство. В условиях каждого из предложений выполнено (46), что влечет (38) и, как следствие, (40). Отсюда, в случае выполнения (47), имеет место соотношение (5), что согласно теореме 1 достаточно для устойчивости. Если точка покоя устойчива, то в условиях каждого из предложений необходимо выполнено (44), либо (45) [13]. Тогда с точностью до устранимых особенностей необходимо выполнено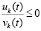 
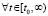. Таким образом, условия (44) –(46) необходимы для устойчивости точки покоя, следовательно, они необходимы для асимптотической устойчивости. Для асимптотической устойчивости выполнение (48), или же эквивалентного соотношения (49), достаточно в сочетании с выполнением (47), поскольку это влечет (6). Если точка покоя асимптотически устойчива, то 
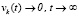, тогда согласно (3) 
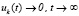, что эквивалентно (48) и (49), таким образом, эти условия необходимы. Оба предложения доказаны.
Пусть относительно системы (1) рассматривается случай, когда в R0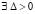 
, такое, что 
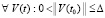выполняются неравенства
, 
,
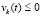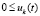
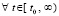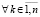, (50)
или
, 
,
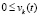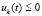
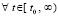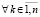. (51)
Неравенства (50) и (51) можно объединить в одно неравенство
, 
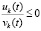
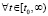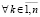, (52)
где с учетом (3) возможны только устранимые особенности. Пусть, кроме того,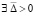 
, такое, что 
, 
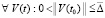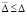, выполняется соотношение
(
) 
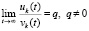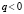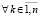. (53)
В совокупности данных условий имеет место
Предложение 3. Пусть для системы (1)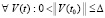 
выполнено любое из соотношений (50), (51). Если 
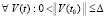каждый компонент правой части (1) и его производная сохраняют знак (в виде нестрогого неравенства) 
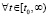, то точка покоя системы (1) устойчива. Если, кроме того, 
, 
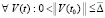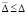, выполнено (53), то для ее асимптотической устойчивости и необходимо, и достаточно, чтобы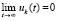 
.
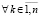Доказательство. Если выполнено (50) или (51), то верно (52), и устойчивость следует из (7). С учетом (50), (51) и сохранения знака в этих соотношениях (в виде нестрогого неравенства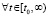 
) 
, 
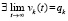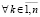[13]. Тогда из (53) 
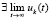, в этом случае необходимым условием устойчивости, следовательно, и асимптотической устойчивости является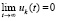 
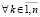[13]. Отсюда с учетом (52) выполнение (53) возможно только, если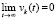 
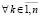, и соотношение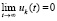 
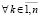оказывается достаточным условием асимптотической устойчивости точки покоя системы (1). Предложение доказано.
Пусть для системы (1) рассматриваются условия, при которых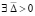 
, такое, что выполняются тройки неравенств
, 
, 
,
, 
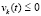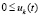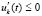
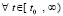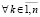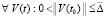, (54)
или
, 
, 
,
, 
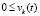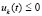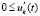
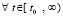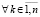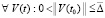. (55)
Имеет место
Предложение 4. Пусть в рассматриваемых условиях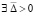 
, такое, что выполняются соотношения (54) или (55). Тогда точка покоя системы (1) устойчива и 
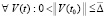необходимо выполняется (38). Для асимптотической устойчивости точки покоя необходимо, чтобы решение было устойчиво и 
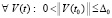выполнялось (39).
Следствие 8. В условиях предложения 4 точка покоя системы (1) устойчива и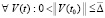 
необходимо выполнять соотношение (40). Для асимптотической устойчивости точки покоя необходимо, чтобы решение было устойчиво и существовало 
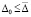, такое, что 
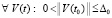выполняется соотношение (41).
Доказательство. Достаточность утверждений предложения и следствия относительно устойчивости точки покоя следует из того, что пары неравенств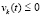 
, 
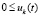или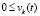 
, 
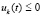обеспечивают ограниченность нулем подынтегральной функции и тем самым выполнение соотношения (7) теоремы 2. С учетом эквивалентности (38) и (40) необходимость этих эквивалентных соотношений следует из неравенств 
, 
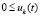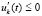или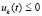 
, 
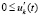. Ввиду эквивалентности (39) и (41) необходимость утверждений относительно асимптотической устойчивости следует из (3). Предложение, а также следствие доказано.
Предложение 4 и следствие 8 дают необходимые условия устойчивости без требования выполнения соотношений (36) или (37).
Имеет место
Теорема 7. Пусть в изначально рассматриваемых для системы (1) условиях теоремы 2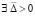 
, такое, что 
, 
, 
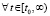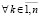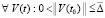выполняются неравенства
, 
, 
,
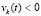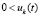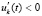или
, 
, 
.
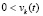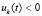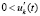Если при этом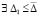 
, такое, что выполняется любое одно из двух условий
1) 
, 
,
,
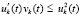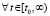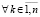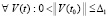
2) 
,
, 
,
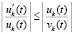
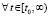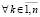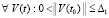то точка покоя системы асимптотически устойчива.
Доказательство. Очевидно,
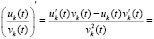
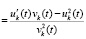. (56)
Отсюда
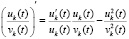. (57)
При выполнении 1) согласно (56)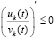 
, поэтому функция 
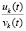не возрастает, с учетом знаков числителя и знаменателя она отрицательна 
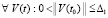, согласно (7) точка покоя устойчива. При выполнении 2) согласно (57) 
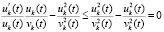, и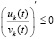 
. Отсюда, как и при выполнении 1), точка покоя устойчива. В обоих случаях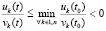 
, 
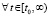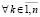, что 
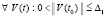обеспечивает выполнение (8). Теорема доказана.
При излагаемых ниже дополнительных ограничениях условия устойчивости (38) и асимптотической устойчивости (39) теоремы 5 сделаются необходимыми и достаточными.
Пусть в условиях теоремы 2 рассматриваются соотношения (38) и (7), а также (39) и (8). Пары соотношений (38) и (7) будут выполняться одновременно, если
,
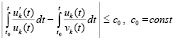
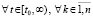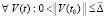, (58)
или, с переходом к первообразным,
,
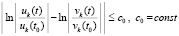что равносильно
,
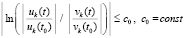или
.
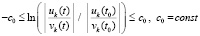Последнее соотношение равносильно неравенствам
,
,
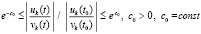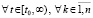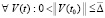, (59)
где по построению с0 – произвольно выбираемая положительная константа,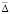 
из теоремы 2. Неравенства (58) и (59) равносильны. Следовательно, при выполнении (59) соотношения (38) и (7) выполняются одновременно, и соотношение (38) оказывается необходимым и достаточным вместе с (7) условием устойчивости. Из (59) также ясно, что выполнение этого соотношения в случае 
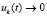возможно только, если 
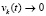, иначе нарушится левая часть соотношения – 
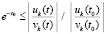. Обратно, если 
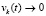, то необходимо 
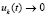, иначе нарушится правая часть соотношения – 
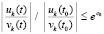(то же следует из (3)). В результате при выполнении (59) вместе с (39) выполняется (8), и выполнение (39) наряду с (8) оказывается необходимым и достаточным условием асимптотической устойчивости.
Таким образом, имеет место следующее.
Теорема 8. Пусть выполнены условия теоремы 2, и пусть в рассматриваемых условиях, включающих, в частности, (33), (34), выполнено соотношение (59). Тогда для устойчивости точки покоя системы (1) необходимо и достаточно существование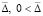 
, такого, что
,
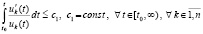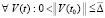. (60)
В том же ограничении для асимптотической устойчивости точки покоя необходимо и достаточно, чтобы выполнялось предыдущее утверждение и нашлось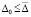 
, такое, что
,
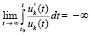
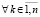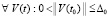. (61)
В силу эквивалентности в рассматриваемых условиях теорем 2 и 1, а также теорем 6 и 5 теорема 8 переходит в следующее утверждение.
Следствие 9. В условиях теоремы 8 для устойчивости точки покоя системы (1) необходимо и достаточно, чтобы нашлось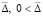 
, такое, что
,
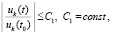
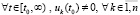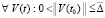. (62)
В том же ограничении для асимптотической устойчивости точки покоя необходимо и достаточно, чтобы выполнялось предыдущее утверждение и нашлось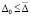 
, такое, что
,
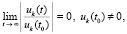
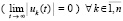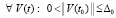. (63)
Замечание 3. Как отмечалось, при выполнении (59), если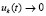 
, то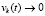 
.
С переходом к первообразным теорема 8 перейдет в утверждение, по форме сохраняющее соотношения (42), (43). Ввиду новых условий для этих соотношений и их значения для описания эксперимента утверждение полностью формулируется заново.
Следствие 10. В условиях теоремы 8 утверждения этой теоремы сохраняются, если соотношения (60) и (61) заменить соответственно на соотношения
,
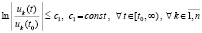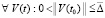(64)
и
,
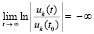
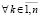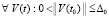. (65)
Замечание 4. Нетрудно видеть, что на основе изложенной схемы можно конструировать аналоги теоремы 8 и следствия 9 для производных правой части системы (1) произвольного порядка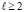 
, если только эти производные существуют. В этом случае соотношение (60) заменится на соотношение
,
,
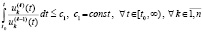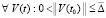соотношение (61) – на соотношение
,
, 
.
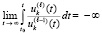
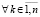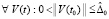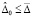Данные соотношения будут означать необходимые и достаточные условия устойчивости и асимптотической устойчивости при ограничении
.
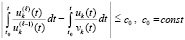
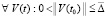Потребуется, кроме того, предполагать аналог (34), чтобы исключить неустранимые особенности подынтегральной функции:
.
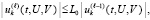
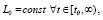
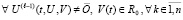После перехода к первообразным будут получаться аналоги (62), (63), составленные из дробей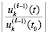 
, а также, на этой основе, – аналоги (64), (65).
О применении необходимых и достаточных условий устойчивости. Предложенные оценки устойчивости с учетом знаков компонентов решения и их двух первых производных так или иначе сводятся к применению теорем 1 и 2. Как правило, они являются частными случаями данных теорем, а также теоремы 8 и следствия 9. Теоремы 1, 2, будучи эквивалентными (в отмеченных ограничениях), дают необходимые и достаточные условия устойчивости и асимптотической устойчивости в сравнительно общем случае. По ходу их вывода получаются аналитические представления этих условий – (5), (6) и (7), (8). Для несобственного интеграла в (7), (8) существует первообразная, посредством которой интеграл на полуоси выражается через логарифм от модуля решения из соотношений (31) и (32). В процессе приближенного решения задачи Коши (1), например, по методу Эйлера, приближение каждого компонента решения становится известным на каждом шаге приближения, равно как становится известным отношение компонента решения к фиксированному начальному значению этого же компонента. На этой основе соотношения (5), (6) численно моделируются в процессе компьютерной реализации. Решение может быть реализовано для нескольких начальных значений в окрестности нулевого начального вектора, в результате будут численно моделироваться необходимые и достаточные условия устойчивости и асимптотической устойчивости. Интегральные оценки теоремы 2 численно моделируются аналогично, с той разницей, что вместо отношения компонента решения к его начальному значению берется логарифм от модуля этого отношения согласно (31) и (32). По такой же схеме интегральные соотношения (60) и (61) теоремы 8 реализуются либо по следствию 9 как соотношения (62), (63), либо по следствию 10 как соотношения (64), (65), – без аналитического вычисления производной правой части системы (1) из (4).
Соотношения теоремы 2 и теоремы 8 непосредственно в аналитическом виде применимы для теоретических оценок устойчивости на основе теорем сравнения, изложенных в [11], а также в [12] и [13], где даны примеры их применения. Для конкретной системы пример приводится ниже по ходу описания численного эксперимента, где помимо того представлены программные реализации интегральных соотношений на основе логарифмических соотношений (31) и (32), а также (64) и (65).
Для линейных систем ОДУ не требуется проверять рассматриваемые соотношения теорем 1 и 2, а также теоремы 8 и следствия 9 в Δ-окрестности нулевого начального вектора – достаточно проверить их выполнение для любого отдельно взятого решения, соответствующего начальному вектору со всеми ненулевыми компонентами [12]. Это непосредственно ясно из того, что в рассматриваемых ограничениях теорема 2 эквивалентна теореме 1, достаточно проверки соотношений (5), (6). Вместе с тем известно [1], что для устойчивости линейной системы необходимо и достаточно, чтобы было ограничено любое одно ненулевое решение. Ограниченность одного решения имеет место одновременно с ограниченностью левой части (5) при ненулевых значениях начальных компонентов. Известно также [1], что отдельно взятое решение линейной системы стремится к нулю тогда и только тогда, когда все решения стремятся к нулю. Такое свойство имеет место одновременно с выполнением (6) для одного произвольно выбранного решения с ненулевыми компонентами начального вектора. Аналогично, в случае соотношений (31), (32). Наконец в условиях теоремы 8 и следствия 9 соотношения (60), (61) выполняются одновременно с (7), (8) соответственно, а значит, и одновременно с (5), (6), аналогично, – для соотношений (62), (63), а также (64) и (65).
Для линейных систем можно применять условия устойчивости, которые полностью не зависят от начальных значений [8, 9], что отмечается также в [10, 11] и в [12, 13], ниже это иллюстрируется при описании численного эксперимента.
Численное моделирование необходимых и достаточных условий устойчивости по ходу решения системы. Пусть для примера рассматривается система
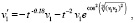(66)
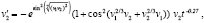
где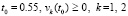 
.
Требуется оценить устойчивость точки покоя. Из (66)
,
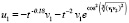где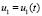 
. Аналогично,
.
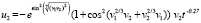Для уравнений системы выполнены неравенства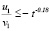 
, 
.
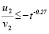Отсюда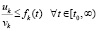 
,
где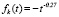 
, 
.
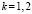По теореме сравнения, данной в [11, 12], точка покоя системы (66) асимптотически устойчива. Это и непосредственно ясно из теоремы 2 и (7), (8):
.
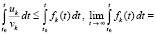
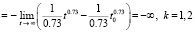Асимптотическую устойчивость подтверждает компьютерная реализация. На Delphi запрограммировано решение задачи (66) по методу Эйлера на отрезке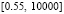 
с шагом 
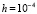. На выходе программы формируются компоненты левых частей (5) (без деления получался бы знак компонента решения, что для краткости закомментировано). Выводится эвклидова норма (norma (V/V0)) от обоих компонентов 
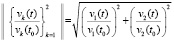. Выводятся значения интегралов (INTEGRAL(v1/v10), INTEGRAL(v2/v20)) компонентов левой части (7), выраженные через первообразные согласно (31). Аналогично, формируются компоненты левых частей (62) (что также закомментировано), выводится их эвклидова норма (norma (U/U0)), значения интегралов (INTEGRAL(u1/u10), INTEGRAL(u2/u20)) компонентов левой части (60) в выражении через логарифмы согласно (64).
program RAE11NORMALOGVUnew1;
{$APPTYPE CONSOLE}
uses
SysUtils;
const h = 0.0001; tt=10000000;
var t,t0,v1,v2,v10, v20,u10, u20: extended; k: longint;
function u1(t,v1,v2:extended):extended;
begin
u1:=-v1*exp(-0.18*ln(t))-1/sqr(t)*v1*exp(sqr(cos(exp(1/3*ln(sqr(v1*v2))))))
end;
function u2(t,v1,v2:extended):extended;
begin
u2:=-exp(sqr(sin(exp(1/7*ln(sqr(v1*v2))))))*
(1+ sqr(cos(exp(1/3*ln(sqr(v1)))*v2+exp(1/3*ln(sqr(v2)))*v1)))*v2*exp(-0.27*ln(t))
end;
begin
k := 0; t0:=0.55; v10:=-0.005*0.005; v20:=0.00005*0.005;
u10:=u1(t0,v10,v20); u20:=u2(t0,v10,v20);
v1:=v10; v2:=v20; t:=t0; while t <=10000 do
begin
v1:= v1+ h * u1(t,v1,v2); v2:= v2+ h * u2(t,v1 ,v2 );
k:=k+1; if k = tt then
begin
writeln (‘t=’,t:4,’ ‘);
writeln (‘norma (V/V0)=’, sqrt(sqr(v1/v10)+sqr(v2/v20)):4,’ ‘,
‘norma (U/U0)=’, sqrt(sqr(U1(t,v1,v2)/U10)+sqr(U2(t,v1,v2)/U20)):4,’ ‘);
writeln ({‘v1/v10=’,v1/v10:4,’ ‘,}’INTEGRAL(v1/v10)=’, ln(abs(v1/v10)):4,’ ‘,
{‘u1/u10=’,u1(t,v1,v2)/u10:4,’ ‘,}’INTEGRAL(u1/u10)=’, ln(abs(u1(t,v1,v2)/u10)):4,’ ‘);
writeln ({‘v2/v20=’,v2/v20:4,’ ‘,}’INTEGRAL(v2/v20)=’, ln(abs(v2/v20)):4,’ ‘,
{‘u2/u20=’,u2(t,v1,v2)/u20:4,’ ‘,}’INTEGRAL(u2/u20)=’, ln(abs(u2(t,v1,v2)/u20)):4,’ ‘);
writeln;
k:=0 end;
t:=t+h;
end;
readln
end.
Результаты работы программы:
t= 1.0E+0003
norma (V/V0)= 2.3E-0155 norma (U/U0)= 6.5E-0157
INTEGRAL(v1/v10)=-3.6E+0002 INTEGRAL(u1/u10)=-3.6E+0002
INTEGRAL(v2/v20)=-4.2E+0002 INTEGRAL(u2/u20)=-4.2E+0002
t= 2.0E+0003
norma (V/V0)= 2.8E-0272 norma (U/U0)= 7.2E-0274
INTEGRAL(v1/v10)=-6.3E+0002 INTEGRAL(u1/u10)=-6.3E+0002
INTEGRAL(v2/v20)=-7.0E+0002 INTEGRAL(u2/u20)=-7.0E+0002
t= 3.0E+0003
norma (V/V0)= 1.2E-0378 norma (U/U0)= 2.9E-0380
INTEGRAL(v1/v10)=-8.7E+0002 INTEGRAL(u1/u10)=-8.7E+0002
INTEGRAL(v2/v20)=-9.4E+0002 INTEGRAL(u2/u20)=-9.5E+0002
t= 4.0E+0003
norma (V/V0)= 1.1E-0478 norma (U/U0)= 2.6E-0480
INTEGRAL(v1/v10)=-1.1E+0003 INTEGRAL(u1/u10)=-1.1E+0003
INTEGRAL(v2/v20)=-1.2E+0003 INTEGRAL(u2/u20)=-1.2E+0003
t= 5.0E+0003
norma (V/V0)= 3.0E-0574 norma (U/U0)= 6.4E-0576
INTEGRAL(v1/v10)=-1.3E+0003 INTEGRAL(u1/u10)=-1.3E+0003
INTEGRAL(v2/v20)=-1.4E+0003 INTEGRAL(u2/u20)=-1.4E+0003
t= 6.0E+0003
norma (V/V0)= 2.0E-0666 norma (U/U0)= 4.1E-0668
INTEGRAL(v1/v10)=-1.5E+0003 INTEGRAL(u1/u10)=-1.5E+0003
INTEGRAL(v2/v20)=-1.6E+0003 INTEGRAL(u2/u20)=-1.6E+0003
t= 7.0E+0003
norma (V/V0)= 7.1E-0756 norma (U/U0)= 1.4E-0757
INTEGRAL(v1/v10)=-1.7E+0003 INTEGRAL(u1/u10)=-1.7E+0003
INTEGRAL(v2/v20)=-1.8E+0003 INTEGRAL(u2/u20)=-1.8E+0003
t= 8.0E+0003
norma (V/V0)= 6.5E-0841 norma (U/U0)= 4.9E-0842
INTEGRAL(v1/v10)=-1.9E+0003 INTEGRAL(u1/u10)=-1.9E+0003
INTEGRAL(v2/v20)=-1.9E+0003 INTEGRAL(u2/u20)=-1.9E+0003
t= 9.0E+0003
norma (V/V0)= 2.0E-0916 norma (U/U0)= 1.5E-0917
INTEGRAL(v1/v10)=-2.1E+0003 INTEGRAL(u1/u10)=-2.1E+0003
INTEGRAL(v2/v20)=-2.1E+0003 INTEGRAL(u2/u20)=-2.1E+0003
Из распечатки видно, что обе выводимые нормы убывают к нулю на отрезке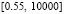 
и одновременно интегралы убывают к 
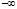. Полученные результаты указывают на признаки асимптотической устойчивости согласно (5), (6), а также согласно (7), (8). Кроме того, это согласуется с (62), (63), а также с (60), (61). Аналогичного вида признаки воспроизводятся в ненулевых точках любой не большей по диаметру окрестности (t0:=0.55; v10:=-0.005*0.005; v20:=0.00005*0.005;) нулевого начального вектора, а также на десятикратно удлиненном отрезке приближенного решения.
Если теперь в первом уравнении системы (66) произвести изменение, состоящее в замене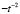 
на +1, и не производить никаких других изменений, то получится система
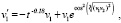(67)
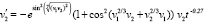
с теми же начальными значениями. Для первого уравнения системы (67) выполнено неравенство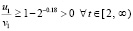 
.
Поэтому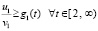 
,
где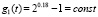 
.
По соответственной теореме сравнения [11, 12] точка покоя системы (67) неустойчива. Это ясно и непосредственно из теоремы 2 и (7):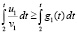 
, где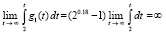 
, отсюда 
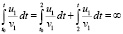, где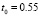 
.
Неустойчивость подтверждает программная реализация. В случае системы (67) в той же программе изменится только описание первой функции (исходная функция закомментирована):
function u1(t,v1,v2:extended):extended;
begin
u1:=-v1*exp(-0.18*ln(t)) + v1*exp(sqr(cos(exp(1/3*ln(sqr(v1*v2))))))
//u1:=-v1*exp(-0.18*ln(t))-1/sqr(t)*v1*exp(sqr(cos(exp(1/3*ln(sqr(v1*v2))))))
end;
function u2(t,v1,v2:extended):extended;
begin
u2:=-exp(sqr(sin(exp(1/7*ln(sqr(v1*v2))))))*
(1+ sqr(cos(exp(1/3*ln(sqr(v1)))*v2+exp(1/3*ln(sqr(v2)))*v1)))*v2*exp(-0.27*ln(t))
end;
Других изменений не будет, за исключением длины отрезка, который теперь задается как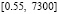 
. Результаты работы измененной программы:
t= 1.0E+0003
norma (V/V0)= 3.7E+0339 norma (U/U0)= 1.6E+0339
INTEGRAL(v1/v10)= 7.8E+0002 INTEGRAL(u1/u10)= 7.8E+0002
INTEGRAL(v2/v20)=-3.8E+0002 INTEGRAL(u2/u20)=-3.8E+0002
t= 2.0E+0003
norma (V/V0)= 8.9E+0656 norma (U/U0)= 4.1E+0656
INTEGRAL(v1/v10)= 1.5E+0003 INTEGRAL(u1/u10)= 1.5E+0003
INTEGRAL(v2/v20)=-5.2E+0002 INTEGRAL(u2/u20)=-5.2E+0002
t= 3.0E+0003
norma (V/V0)= 7.5E+0984 norma (U/U0)= 3.6E+0984
INTEGRAL(v1/v10)= 2.3E+0003 INTEGRAL(u1/u10)= 2.3E+0003
INTEGRAL(v2/v20)=-6.4E+0002 INTEGRAL(u2/u20)=-6.4E+0002
t= 4.0E+0003
norma (V/V0)= 1.3E+1319 norma (U/U0)= 6.4E+1318
INTEGRAL(v1/v10)= 3.0E+0003 INTEGRAL(u1/u10)= 3.0E+0003
INTEGRAL(v2/v20)=-7.5E+0002 INTEGRAL(u2/u20)=-7.5E+0002
t= 5.0E+0003
norma (V/V0)= 6.6E+1657 norma (U/U0)= 3.2E+1657
INTEGRAL(v1/v10)= 3.8E+0003 INTEGRAL(u1/u10)= 3.8E+0003
INTEGRAL(v2/v20)=-8.5E+0002 INTEGRAL(u2/u20)=-8.6E+0002
t= 6.0E+0003
norma (V/V0)= 8.3E+1999 norma (U/U0)= 4.1E+1999
INTEGRAL(v1/v10)= 4.6E+0003 INTEGRAL(u1/u10)= 4.6E+0003
INTEGRAL(v2/v20)=-9.5E+0002 INTEGRAL(u2/u20)=-9.5E+0002
t= 7.0E+0003
norma (V/V0)= 5.7E+2344 norma (U/U0)= 2.8E+2344
INTEGRAL(v1/v10)= 5.4E+0003 INTEGRAL(u1/u10)= 5.4E+0003
INTEGRAL(v2/v20)=-1.0E+0003 INTEGRAL(u2/u20)=-1.0E+0003
Из распечатки видно, что обе выводимые нормы возрастают к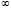 
на отрезке [0.55,7300] и одновременно возрастают к 
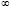оба интеграла от компонентов первого уравнения: INTEGRAL(v1/v10), INTEGRAL(u1/u10). На отрезке большей длины, в частности на [0.55,10000], наступает переполнение. Результаты указывают на признак неустойчивости согласно (5), а также согласно (7). Это согласуется с (60), а также с (62). Аналогичный признак неустойчивости воспроизводится в ненулевых точках любой не большей по диаметру окрестности нулевого начального вектора.
Пусть рассматривается система
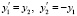. (68)
Система (68) линейна с матрицей постоянных коэффициентов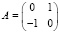 
. Ее характеристический полином 
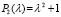имеет два комплексно сопряженных корня – мнимые единицы с противоположным знаком: 
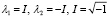, поэтому система устойчива [3], но не асимптотически. Очевидный вывод подтверждает программная реализация. Для системы (68) в исходной программе изменится описание функций, других изменений не требуется:
function u1(t,v1,v2:extended):extended;
begin
u1:=v2
end;
function u2(t,v1,v2:extended):extended;
begin
u2:=-v1
end;
Результаты работы программы с данным изменением:
t= 1.0E+0003
norma (V/V0)= 8.3E+0001 norma (U/U0)= 8.3E+0001
INTEGRAL(v1/v10)=-5.9E-0001 INTEGRAL(u1/u10)= 4.4E+0000
INTEGRAL(v2/v20)= 4.4E+0000 INTEGRAL(u2/u20)=-5.9E-0001
t= 2.0E+0003
norma (V/V0)= 9.3E+0001 norma (U/U0)= 9.3E+0001
INTEGRAL(v1/v10)=-9.8E-0001 INTEGRAL(u1/u10)= 4.5E+0000
INTEGRAL(v2/v20)= 4.5E+0000 INTEGRAL(u2/u20)=-9.8E-0001
t= 3.0E+0003
norma (V/V0)= 2.1E+0001 norma (U/U0)= 2.1E+0001
INTEGRAL(v1/v10)=-2.2E-0002 INTEGRAL(u1/u10)= 3.0E+0000
INTEGRAL(v2/v20)= 3.0E+0000 INTEGRAL(u2/u20)=-2.2E-0002
t= 4.0E+0003
norma (V/V0)= 6.9E+0001 norma (U/U0)= 6.9E+0001
INTEGRAL(v1/v10)=-3.2E-0001 INTEGRAL(u1/u10)= 4.2E+0000
INTEGRAL(v2/v20)= 4.2E+0000 INTEGRAL(u2/u20)=-3.2E-0001
t= 5.0E+0003
norma (V/V0)= 9.9E+0001 norma (U/U0)= 9.9E+0001
INTEGRAL(v1/v10)=-1.8E+0000 INTEGRAL(u1/u10)= 4.6E+0000
INTEGRAL(v2/v20)= 4.6E+0000 INTEGRAL(u2/u20)=-1.8E+0000
t= 6.0E+0003
norma (V/V0)= 4.2E+0001 norma (U/U0)= 4.2E+0001
INTEGRAL(v1/v10)=-9.6E-0002 INTEGRAL(u1/u10)= 3.7E+0000
INTEGRAL(v2/v20)= 3.7E+0000 INTEGRAL(u2/u20)=-9.6E-0002
t= 7.0E+0003
norma (V/V0)= 5.2E+0001 norma (U/U0)= 5.2E+0001
INTEGRAL(v1/v10)=-1.5E-0001 INTEGRAL(u1/u10)= 3.9E+0000
INTEGRAL(v2/v20)= 3.9E+0000 INTEGRAL(u2/u20)=-1.5E-0001
t= 8.0E+0003
norma (V/V0)= 1.0E+0002 norma (U/U0)= 1.0E+0002
INTEGRAL(v1/v10)=-2.9E+0000 INTEGRAL(u1/u10)= 4.6E+0000
INTEGRAL(v2/v20)= 4.6E+0000 INTEGRAL(u2/u20)=-2.9E+0000
t= 9.0E+0003
norma (V/V0)= 6.1E+0001 norma (U/U0)= 6.1E+0001
INTEGRAL(v1/v10)=-2.3E-0001 INTEGRAL(u1/u10)= 4.1E+0000
INTEGRAL(v2/v20)= 4.1E+0000 INTEGRAL(u2/u20)=-2.3E-0001
Из распечатки видно, что обе рассматриваемые нормы не превосходят 9.3E+0001 (93) на всем отрезке [0.55,10000]. При этом оба интеграла не превосходят 4.6E+0000 (4.6). По всем рассматриваемым признакам система устойчива, тогда как признаков асимптотической устойчивости или неустойчивости в численном выражении не наблюдается.
Замечание 5. Как отмечалось, для линейных систем имеются необходимые и достаточные условия устойчивости и асимптотической устойчивости, которые не связаны с какими-либо начальными значениями, условия изложены и обоснованы в [8, 9]. Описание и примеры их применения приводятся в [11–13]. Результаты программной реализации данных условий, как правило, отличаются наглядностью. Так, для системы (68) в [11] приводятся следующие результаты работы программы:
1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000
1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000
………………………………………………………………………………….......
1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000
1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000
Эти данные соответствуют шагу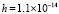 
метода Эйлера и выполнению 75 итераций, которые в приближении к асимптотике достигают значения 
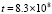. На всем отрезке 
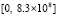округленное значение эвклидовой нормы матрицы 
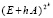, где E – единичная матрица, при каждом значении k не превосходит значения 1.4, что указывает на неасимтотическую устойчивость системы [11].
Замечание 6. В [13] приводится программно реализованное преобразование анализа устойчивости любого ненулевого решения дифференциальной системы к анализу устойчивости точки покоя преобразованной системы. Программная реализация тривиальна, поэтому относительно нее выше не сделано специальных оговорок.
О границах эквивалентности необходимых и достаточных условий устойчивости. Относительно эквивалентности теорем 1 и 2 необходимо отметить следующее. Эти две теоремы эквивалентны только в условиях теоремы 2, которые включают существование и единственность решения задачи Коши (1), но помимо того ещё ограничения (2) и (3). Без этих ограничений теорема 2 не вытекает из преобразований метода Эйлера (11), (12), а затем последующих преобразований, в числе которых (19) и (20)–(31). В то же время теорема 1 допускает принципиально более широкие условия [12], достаточность соотношений (5) имеет место непосредственно в условиях существования решения. В самом деле, если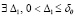 
, такое, что для 
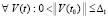верно неравенство
,
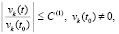
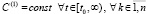то в той же Δ1-окрестности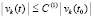 
, и для 
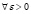выполнено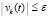 
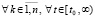, лишь только 
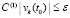. Отсюда 
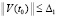, где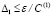 
, влечет 
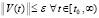. Таким образом, выполнение соотношения (5) является общим достаточным условием устойчивости, не использующим ограничения теоремы 2.
Что касается необходимости условий теоремы 1, то она обосновывается только (другого решения не найдено) исходя из преобразований метода Эйлера (11)–(13), это совпадает с необходимостью условий теоремы 2: соотношения (11)–(13) лежат в основе выполнения соотношений (20)–(31), с помощью которых выводится теорема 2. Более точно, если решение системы (1) устойчиво, то оно отличается от возмущенного решения согласно (12), (13), а это тогда и только тогда, когда верно (14). В свою очередь, корректность построения левой части этого неравенства целиком определяется условиями теоремы 2, которые вытекают из мультипликативных преобразований метода Эйлера. Таким образом, необходимые условия теорем 1 и 2 совпадают, тогда как достаточные условия теоремы 1 фактически выходят за рамки формальных ограничений этой теоремы.
Эквивалентность теорем 2 и 8 имеет место в еще более узких условиях, чем условия теоремы 2: она имеет место при выполнении всех ограничений теоремы 2, а также при дополнительных ограничениях теоремы 8, в частности при выполнении условий (33), (34) и (59). Условия эквивалентности теоремы 8 и следствия 9 можно разграничить подобно тому, как разграничивается эквивалентность теоремы 2 и теоремы 1.
Таким образом, речь об эквивалентности предложенных разновидностей необходимых и достаточных условий устойчивости может идти только при конкретном указании всех используемых ограничений. Различие ограничений существенно. Так, условия теоремы 2, взятые в форме соотношений (31), (32), наглядно исключают случаи смены знака компонентов решений системы (1) – в этих случаях компоненты решения пересекают полуось, поэтому логарифмы от их модуля в (31), (32) не существуют.
В противоположность теореме 2 ограничений на знак компонента решения соотношения (5), (6) теоремы 1 не требуют, их выполнение представляет собой самые общие достаточные условия устойчивости, в частности, для компьютерной реализации. Выполнение этих же соотношений является необходимым лишь при отмечавшихся ограничениях, заимствованных из теоремы 2.
Можно отметить, что предложенные необходимые и достаточные условия устойчивости сохраняют отличие от условий устойчивости известных методов [1–3], представляющих по преимуществу достаточные условия устойчивости, и, аналогично, от условий методов, основанных на компьютерных технологиях [17, 18].
Заключение
В работе построены критерии устойчивости по Ляпунову на основе метода Эйлера приближенного решения ОДУ. Сформулированы необходимые и достаточные условия устойчивости, которые дают возможность численного моделирования устойчивости по ходу решения задачи Коши для ОДУ. Описаны разновидности необходимых и достаточных условий устойчивости, их взаимосвязи и различия, определены формальные ограничения, при которых они корректны, указаны классы дифференциальных систем для их применения. Представлено обоснование предложенных критериев, показана их конструктивность, выполнены численные эксперименты, подтверждающие их достоверность, детализированы способы и особенности программной реализации. Помимо того, получены формализованные оценки устойчивости на основе знаков компонентов решения и двух их производных. Построение оценок опирается на компоненты функции правой части дифференциальной системы и их производные, обоснование оценок, как правило, использует интегральную форму необходимых и достаточных условий устойчивости.
Библиографическая ссылка
Ромм Я.Е. О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ // Современные наукоемкие технологии. – 2022. – № 2. – С. 92-109;URL: https://top-technologies.ru/ru/article/view?id=39043 (дата обращения: 22.11.2024).