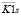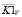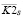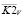Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Воскобойников Ю.Е. 1, 2 Боева В.А. 3

---

1 ФГБОУ ВО «Новосибирский государственный архитектурно-строительный университет (СИБСТРИН)»

2 ФГБОУ ВО «Новосибирский государственный технический университет»

3 ФГБОУ ВО «Новосибирский государственный архитектурно-строительный университет (Сибстрин)»

В последние два десятилетия для описания динамики нелинейных систем в терминах «вход-выход» используются так называемые ряды Вольтерра. Наиболее часто используется квадратичный член ряда, который порождает двумерное ядро и соответствующее двумерное уравнение Вольтерра. Для идентификации двумерной импульсной переходной функции предложен подход, основанный на обращении уравнения Вольтерра и использующий частные и смешанные производные второго порядка от выходного сигнала системы. Принципиальной проблемой реализации этого подхода является устойчивое вычисление частных и смешанных производных второго порядка по зашумленным данным. Для преодоления этой проблемы можно использовать двумерный сглаживающий бикубический сплайн (сокращенно СБС). Однако построение СБС на практике сталкивается с принципиальным затруднением – выбором параметров сглаживания. В случае СБС проблема выбора параметра становится более сложной из-за построения целого ансамбля (набора) кубических (одномерных) сплайнов при сглаживании данных по одной из двух переменных исходных данных. Поэтому в работе вводятся два типа параметров сглаживания СБС: скалярный и векторный. Скалярный параметр является одинаковым для всех кубических сплайнов по заданной переменной. Векторный параметр является вектором, проекции которого определяются как параметры сглаживания для каждого кубического сплайна, т.е. каждый кубический сплайн имеет свой «персональный» параметр сглаживания. В работе предлагаются алгоритмы оценивания оптимальных значений как скалярного, так и векторного параметров при разной априорной информации о дисперсии шума измерения двумерного выходного сигнала идентифицируемой системы. Выполненный вычислительный эксперимент показал хорошую точность оценивания оптимальных параметров сглаживания предложенными алгоритмами выбора.

Статья в формате PDF

435 KB

задача идентификации квадратичного ядра нелинейной системы

сглаживающие бикубические сплайны

скалярный и векторный параметры сглаживания

оценивание оптимальных параметров сглаживания

1. Apartsyn A.S., Solodusha S.V., Spiryaev V.A. Modeling of Nonlinear Dynamic Systems with Volterra Polynomials: Elements of Theory and Applications. Int. J. Energy Optim. Eng. 2013. 2. P. 16–43. DOI: 10.4018/ijeoe.2013100102.

2. Cheng C.M. Volterra-series-based nonlinear system modeling and its engineering applications: A state-of-the-art review. Mechanical Systems and Signal Processing. 2017. Vol. 87. P. 430–364.

3. Солодуша С.В. Численное моделирование динамики теплообмена модифицированным квадратичным полиномом Вольтерры // Вычислительные технологии. 2013. Т. 18. № 2. С. 84–94.

4. Солодуша С.В. Амплитуды тестовых сигналов для построения интегральных моделей динамики объектов тепло- и электроэнергетики // Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта (CAD/CAM/PDM-2017): материалы XVII Международной научно-практической конференции. М.: ООО «Аналитик», 2017. С. 322–326.

5. Solodusha S.V. Quadratic and cubic Volterra polynomials: Identification and application // Vestnik Sankt-Peterburgskogo Universiteta. Prikladnaya Matematika, Informatika, Protsessy Upravleniya. 2018. Vol. 14. No. 2. P. 131–144. DOI: 10.21638/11701/spbu10.2018.205.

6. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1986. 285 с.

7. Воскобойников Ю.Е., Боева В.А. Новый устойчивый алгоритм непараметрической идентификации технических систем // Современные наукоемкие технологии. 2019. № 5. С. 25–29.

8. Воскобойников Ю.Е., Боева В.А. Алгоритмы непараметрической идентификации сложных технических систем // Научный вестник НГТУ. 2020. № 4 (80). С. 47–64. DOI: 10.17212/1814-1196-2020-4-47-64.

9. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. М.: Наука, 1980. 345 с.

10. Wang Y. Smoothing Splines Methods and Applications. Ser. Monographs on Statistics and Applied Probability v. 121. A Chapman & Hall book, 2011. 347 p.

11. Воскобойников Ю.Е., Преображенский Н.Г., Седельников А.И. Математическая обработка эксперимента в молекулярной газодинамике. Новосибирск: Наука, 1984. 238 с.

12. Воскобойников Ю.Е., Боева В.А. Устойчивый алгоритм вычисления смешанных производных в задачах непараметрической идентификации нелинейных систем // Современные наукоемкие технологии. 2021. № 4. С. 25–29. DOI: 10.17513/snt.38610.

13. Воскобойников Ю.Е., Боева В.А. Метод L-кривой для оценивания оптимального параметра сглаживающего кубического сплайна // Международный научно-исследовательский журнал. 2021. № 11 (113). Ч. 1. С. 6–13. DOI: 10.23670/IRJ.2021.113.11.003.

14. Rezghi M., Hosseini S.M. A new variant of L-curve for Tikhonov regularization. J. Comput. Appl. Math. 2012. No. 231 (5). Р. 914–924.

15. Cultrera A., Callegaro L. A simple algorithm to find the L-curve corner in the regularization of ill-posed inverse problems. IOP SciNotes. 2020. Vol. 1. Nо. 2. Р. 32–39.

Два последних десятилетия ведутся интенсивные научные исследования методов идентификации нелинейных динамических систем, представленных различными математическими моделями. Весьма перспективной в этом отношении является интегральная модель «вход-выход», состоящая из нескольких уравнений Вольтерра, ядра которых образованны из соответствующих слагаемых ряда Вольтерра [1, 2]. Особенно часто используется ряд, ограниченный квадратичным членом ряда Вольтерра [3]. В этом случае связь между входным сигналом φ(τ) моделируемой стационарной системы и ее выходным сигналом f(t) можно представить следующим интегральным соотношением [3]:

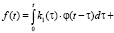
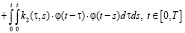,(1)

где k1(τ), k2(τ,s) – линейное и квадратичное ядра Вольтерра соответственно. Нужно идентифицировать эти ядра по измеренным значениям входного и выходного сигналов идентифицируемой системы.

Очевидно, что сигнал f(t) есть сумма двух неизвестных сигналов f1(t) и f2(t) – первое и второе слагаемые в (1), которые можно интерпретировать как выходные сигналы линейной и квадратичной «подсистем». Следовательно, на первом этапе идентификации необходимо выделить из f(t) сигналы f1(t), f2(t) по отдельности. Для произвольного входного сигнала такая задача неразрешима. В работах [4, 5] предложена эффективная методика такого разделения, которая подразумевает проведение активной идентификации, когда на вход системы подаются прямоугольные сигналы заданной формы и заданной амплитуды. В результате получаем следующие интегральные соотношения:

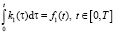(2)

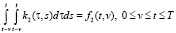(3)

Из выражения (2) следует известная формула:

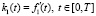(4)

а из (3) – формула обращения [4, 6]:

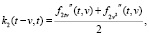(5)

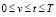
где используются следующие обозначения:

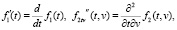
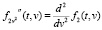(6)

К сожалению, реализация на практике полученных формул обращения сталкивается с принципиальной трудностью – некорректностью операции дифференцирования [6]. Одно из проявлений некорректности заключается в больших ошибках вычисления производной даже при очень малых погрешностях задания значений дифференцируемой функции. Таким образом, устойчивое дифференцирование зашумленных данных становится актуальной задачей для реализации формулы (5) на практике.

В работе [7] был построен алгоритм идентификации на основе формулы (4), где для устойчивого вычисления первой производной использовался сглаживающий кубический сплайн (СКС) дефекта единица с выбором параметра сглаживания из условия минимума среднеквадратической ошибки сглаживания. Алгоритм показал приемлемую точность идентификации при решении практических задач [8]. В случае идентификации квадратичного ядра k2(τ,s) использование сглаживающих сплайнов существенно усложняется. Во-первых, для вычисления смешанной производной второго порядка 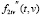нужно строить уже сглаживающий бикубический сплайн (СБС), являющийся функцией двух переменных t, v. Во-вторых, из-за разной «гладкости» функции f2(t, v) по разным переменным необходимо выбрать уже несколько параметров сглаживания из условия минимума ошибки сглаживания. В-третьих, в большинстве случаев дисперсия шума (погрешностей) измерения функции f2(t, v) неизвестна.

Эти затруднения обусловили следующие основные задачи, которые не получили своего решения в соответствующих научных публикациях и которые решаются в данной работе:

− введение нескольких типов параметров сглаживания – скалярного и векторного параметров для СБС;

− раздельный выбор параметров сглаживания (по каждой переменной сплайна) из условия минимума ошибки сглаживания при неизвестной дисперсии шума измерения на основе метода L-кривой;

− исследование эффективности предложенных алгоритмов выбора с точки зрения минимизации ошибки сглаживания.

Материалы и методы исследования

Предположим, что значения двумерной функции f2(t, v) измеряются при значениях аргументов ti , i = 1…Nt , vj , j = 1…Nv, т.е. в узлах прямоугольной сетки {ti, vj}, i = 1…Nt, j = 1…Nv. Заметим, что узлы ti, и τj могут иметь неодинаковый и неравный шаг, что встречается в реальных экспериментах.

Для учета возможных погрешностей (шумов) измерений принимается следующая модель измеренных значений :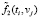

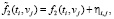
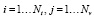(7)

где ηij – случайный шум измерения с нулевым средним и дисперсией сетки {ti, vj} (равноточные измерения). Требуется по исходным данным 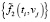вычислить значения производных 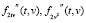в заданных узлах сетки {ti , vj}, i = 1…Nt, j = 1…Nv.

Замечание. Из вида интеграла (3) следует, что функция f2(t, v) принимает ненулевые значения для аргументов, удовлетворяющих условию v ≤ t. Для отрицательных значений v, t функция равна нулю в силу условия технической реализуемости системы, т.е.: k2(t, v) ≡ 0, если v < 0, t < 0. Так как значения производных в (5) используются только при v ≤ t, то для устранения разрыва первого рода при значениях v = t предлагается дополнить значения функции f2(t, v) для v > t по правилу:

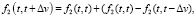
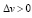(8)

Дополненную таким образом функцию будем обозначать как .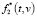

Для устойчивого вычисления производных 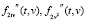обратимся к сглаживающим кубическим сплайнам (СКС) [9], широко используемым при обработке экспериментальных данных [10, 11], включая задачи идентификации [8]. Алгоритм построения двумерного сглаживающего бикубического сплайна как построение ансамбля (набора) одномерных СКС был изложен в работе [12]. Поэтому здесь кратко опишем основные шаги этого алгоритма, необходимые для понимания места и способов выбора параметра сглаживания. Сделаем это для нахождения смешанной производной 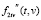, так как вычисление частной производной второго порядка 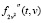сводится к двукратному дифференцированию одномерного сплайна с аргументом v.

Шаг 1. Для каждого j = 1…Nv формируется набор данных (фиксируется значение vj):

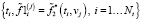(9)

выбирается параметр сглаживания α1(j), и по исходным данным (9) строится СКС 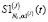, допускающий на отрезках [ti, ti+1), i = 1…Nt – 1 представление:

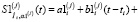
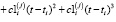(10)

и имеющий непрерывную вторую производную (по переменной t) на всем интервале 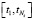. По сплайну (10) вычисляются значения первой производной 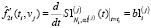(оценка для производной 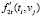). Шаг 1 повторяется для vj , j = 1…Nv и таким образом строится ансамбль (набор) из Nv одномерных СКС, каждому из которых необходимо задать параметр сглаживания α1(j), j = 1…Nv.

Шаг 2. Для каждого i = 1…Nt формируется набор данных (фиксируется значение ti):

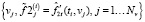(11)

выбирается параметр сглаживания α2(j) и строится СКС 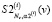, первая производная которого является оценкой 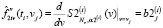для смешанной производной 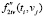, где 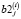– коэффициент сплайна 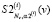в представлении:

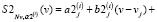
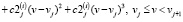(12)

Шаг 2 повторяется для ti, i = 1…Nt, и таким образом строится ансамбль (набор) из Nt одномерных СКС, каждому из которых необходимо задать параметр сглаживания α2(j), i = 1…Nt.

Введем для СБС два новых понятия: скалярный и векторный параметр сглаживания. Под скалярным параметром будем понимать параметр, величина которого одинакова для всех сплайнов данного ансамбля. Так, на шаге 1 скалярный параметр определяется как

α1(j) = α1, j = 1…Nv , (13)

Векторный параметр сглаживания – это вектор, каждая проекция которого задает свой параметр сглаживания соответствующему СКС из ансамбля сплайнов. Так, на шаге 2 векторный параметр 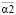имеет i-ю проекцию, равную

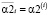. (14)

Возникает главный вопрос при построении сплайнов на практике: как выбрать скалярный или векторный параметры сглаживания? При ответе на этот вопрос существенное значение играет наличие достоверной информации о дисперсии шума измерений 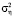(7).

Первоначально предположим, что дисперсия 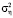шума измерения известна с точностью 5–10 %. В этом случае для выбора скалярного параметра сглаживания можно использовать алгоритм, основанный на проверке статистической гипотезы об оптимальности параметра сглаживания и предложенный в работе [11]. Для проверки этой гипотезы (предположим, что для шага 1) вводится критерий

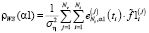(15)

где 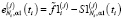– невязка i-го измерения в j-м сплайне 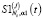(9). В качестве скалярного параметра сглаживания α1 принимается значение α1W, для которого выполняется неравенство

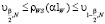(16)

где величины 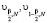– квантили χ2-рас-пределения с N = Nt · Nv степенями свободы уровней β/2 и 1 – (β/2) соответственно. Величина β определяет вероятность ошибки первого рода при проверке гипотезы об оптимальности (величина среднеквадратической ошибки сглаживания) оценки α1W и, как правило, β = 0.05. Если N > 30, то для вычисления квантилей χ2-распределения при β = 0.05 можно использовать простые формулы:

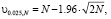
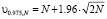(17)

Вычисление α1W сводится к решению нелинейного уравнения

ρWS(α1) = N, (18)

итерационными алгоритмами. В качестве α1W принимается приближённое решение уравнения (18), которое удовлетворяет неравенству (16). Вычислительный эксперимент показал [12], что рассмотренный алгоритм выбора скалярного параметра позволяет с приемлемой точностью (увеличение ошибки сглаживания по сравнению с минимальной 6–10 %) оценить оптимальный скалярный параметр сглаживания α1opt, минимизирующий среднеквадратическую ошибку (СКО) фильтрации.

Такой же алгоритм выбора можно построить для вычисления проекций векторного параметра сглаживания. В качестве j-й проекции вектора 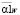принимается значение 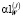, удовлетворяющее неравенству

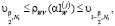(19)

где

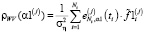(20)

Вычисление 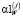сводится к решению нелинейного уравнения

ρWV(α1(j)) = N, (21)

итерационными алгоритмами. В качестве 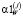принимается приближённое решение уравнения (21), удовлетворяющее неравенству (19). Результаты сравнения ошибок сглаживания при использовании этих двух типов параметров сглаживания приводятся ниже.

Заметим, что вычисление как скалярного, так и векторного параметров сглаживания на основе проверки статистической гипотезы об оптимальности параметра требует задания достоверной величины дисперсии шума измерения. При заниженном значении дисперсии вычисляется заниженное значение (по сравнению с оптимальным) параметра сглаживания, что приводит к «недостаточной» фильтрации шума измерения – высокий уровень «остаточного» шума. При завышенной дисперсии наблюдается обратный эффект – сглаживаются «тонкие» структуры обрабатываемого сигнала. К сожалению, ситуация достоверного знания дисперсии шума измерения в реальном физическом эксперименте скорее исключение, чем правило. Кроме того, при вычислении смешанной производной на шаге 2 сплайны строятся по результатам дифференцирования на шаге 1, которые содержат «шум дифференцирования» неизвестной дисперсии. Все это говорит об актуальности разработки алгоритмов выбора параметров сглаживания для случая неизвестной дисперсии шума измерения, которые и составляют предмет дальнейших исследований.

В работе [13] был построен алгоритм выбора параметра сглаживания одномерного СКС на основе метода L-кривой, позволяющий с приемлемой точностью оценить оптимальный параметр сглаживания как в случае некоррелированного, так и для коррелированного шума измерений. Сам метод L-кривой иногда используется для выбора параметра регуляризации в алгоритмах решения некорректных задач (например, [14–15]), когда неизвестны характеристики погрешностей исходных данных. Поэтому попытаемся модифицировать алгоритм выбора параметра сглаживания работы [13] для вычисления скалярного и векторного параметров сглаживания.

В случае одномерного СКС в качестве параметра сглаживания принималась величина αL, являющаяся решением вариационной задачи:

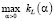(22)

Кривизна kL(α) L-кривой определяется по формуле

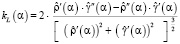(23)

где

,

;

.

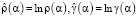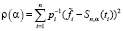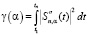Одномерный СКС Sn,α(ti) строился по набору данных 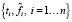, а весовые множители pi в случае равноточных измерений задаются одинаковыми, например pi = 1. Для эффективного вычисления функционала γ(α) (куда входит вторая производная сплайна) в работе [13] предложена формула

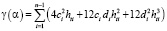(24)

где hti = ti+1 – ti, i = 1…n–1, ci , di – коэффициенты СКС, вычисленные при заданном параметре α.

Такой же алгоритм выбора можно построить для вычисления проекций векторного параметра сглаживания (для определенности на шаге 2). В качестве i-й проекции вектора 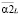принимается значение 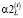, доставляющее максимум кривизны kL(α) L-кривой (23), вычисленной для сплайна 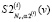. В этом случае функционалы ρ(α), γ(α) для этого сплайна определяются выражениями

;

,

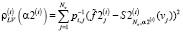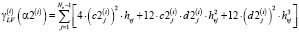где hvj = vj+1 – vj, j = 1…Nv – 1, – коэффициенты сплайна .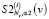

Для вычисления скалярного параметра сглаживания (для определенности на шаге 2) определим функционалы ρ(α), γ(α) следующим образом:

,

,

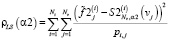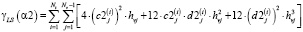где pi,j – весовые множители для i, j-го измерения (для равноточных измерений задаются одинаковыми), 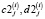– коэффициенты сплайна 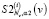, построенного при параметре α2, hvj = vj+1 – vj, j = 1…Nv – 1.

Далее в соответствии с (23) находится значение кривизны и, решая вариационную задачу (22), находим значение α2L, при котором кривизна L-кривой максимальна, и это значение является скалярным параметром сглаживания бикубического сплайна.

Результаты исследования и их обсуждение

В качестве «тестового» квадратичного ядра Вольтерра k2(τ,s) (уравнение (1)) была принята функция, изображенная на рис. 1 и часто используемая для моделирования энергетических объектов [5]. Был выполнен обширный вычислительный эксперимент по идентификации этого ядра. В силу ограниченности объема статьи кратко рассмотрим только результаты эксперимента, связанные с вычислением смешанной производной 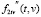функции f2(t, v) (уравнение (3)) по бикубическому сплайну со скалярным и векторным параметрами сглаживания при неизвестной дисперсии шума измерения. Эта ситуация является более сложной и наиболее типичной в реальном эксперименте. При этом основное внимание уделяется исследованию эффективности скалярного и векторного параметров сглаживания, которая характеризует, насколько увеличивается ошибка сглаживания при этих параметрах по сравнению с оптимальными скалярным и векторным параметрами сглаживания. На рис. 2 показана смешанная производная 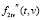, имеющая достаточно сложную форму. Параметры используемой сетки {ti, vj}: Nt = 80, Nv = 80, ti = 0.03·(i – 1), i = 1…Nt , vj = 0.03·(j – 1), j = 1…Nv . В качестве краевых условий на всех четырех границах прямоугольной области задавались нулевые вторые производные.

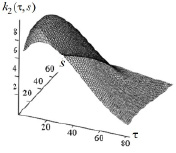
Рис. 1. Квадратичное ядро k2(τ,s)

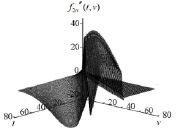
Рис. 2. Смешанная производная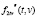

Точные значения «дополненной» функции 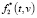(замечание 1) в узлах сетки {ti, vj} (матрица F* с элементами 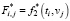) искажались нормально распределенным шумом с нулевым средним и дисперсией 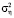(7). Относительный уровень δη шума измерения определялся выражением

,

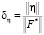где || || означает евклидову норму матрицы. Сформированная таким образом матрица 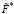с элементами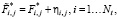 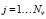является исходной для построения СБС. Так как параметры кубических сглаживающих сплайнов задаются на шаге 1 (параметр сглаживания α1(j)) и шаге 2 (α2(i)), то здесь же определялись и относительные ошибки сглаживания:

• на шаге 1:

скалярная

;

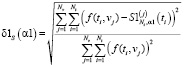векторная

;

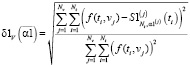• на шаге 2:

скалярная

;

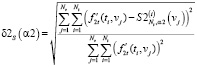векторная

.

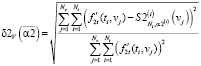Очевидно, что на шаге 2 определяется уже относительная ошибка сглаживания первой производной. Обозначим через 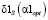, , 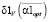, 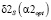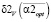– наименьшие относительные ошибки сглаживания при использовании оптимальных параметров сглаживания. Аналогично величины 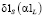, , 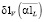, 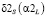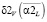определяют относительные ошибки при выборе параметров на основе метода L-кривой описанными выше алгоритмами. Для количественного сравнения относительных ошибок сглаживания введем следующие коэффициенты эффективности:

; ;

; .

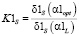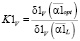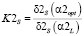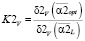Очевидно, что эти коэффициенты меняются в интервале от 0 до 1 и их значения являются случайными величинами. Поэтому по выборке объемом 30 вычислялись выборочные средние 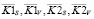. Чем больше эти средние отклоняются от 1 в меньшую сторону, тем больше проигрыш по точности сплайна, построенного с параметрами 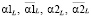. Средние значения коэффициентов эффективности приведены в таблице для трех уровней шума: 0,02; 0,04; 0,06. Анализ этой таблицы показывает, что:

− векторный параметр сглаживания имеет меньший коэффициент эффективности по сравнению со скалярным параметром при прочих равных условиях построения сглаживающих сплайнов;

− с увеличением уровня шума измерения наблюдается уменьшение значений коэффициентов эффективности;

− коэффициент эффективности при сглаживании функции больше соответствующего коэффициента эффективности при сглаживании производных.

Средние значения коэффициентов эффективности

Заключение

Предложенные алгоритмы вычисления скалярного и векторного параметров сглаживания позволяют с приемлемой точностью оценить оптимальные значения этих параметров даже при неизвестных дисперсиях шума измерений. Это позволяет при построении бикубических сплайнов учитывать (за счет выбора двух параметров сглаживания) разную гладкость дифференцируемой функции по отдельным переменным, что уменьшает ошибку вычисления смешанных производных в задаче идентификации квадратичного ядра Вольтерра.

Исследование выполнено при финансовой поддержке РНФ в рамках научного проекта № 22-21-00409.

Библиографическая ссылка