Наряду с появлением интернет-магазинов появились и первые поисковые системы товаров [1]. Несмотря на большие возможности поисковых систем в электронной коммерции, они функционально ограничены. Так, например, в проектах с малым бюджетом компаний, которые не способны обеспечить себе штат программистов, используются зарубежные системы, не способные корректно разбирать строки, содержащие нелатинские символы, а также учитывать семантику и фонетику слов. В то время как учёт семантики (смысла) слов в поисковых алгоритмах торговых сервисов не имеет практической ценности из-за низкой производительности алгоритмов и малой эффективности, получить фонетику (звучание) слова можно для любого языка, используя стандартизированный процесс транслитерации [2]. Зачастую поиск на сайтах ограничен точным линейным поиском, предполагающим разбиение строк с помощью разделителя (обычно пробел) [3].
Необходимая стратегия поиска должна предполагать работу с неструктурированной базой наименований продукции для осуществления поисковой задачи. Такие базы актуальны на сегодняшний день из-за появления большого числа источников информации, таких как открытые веб-сайты, устаревшие базы данных (не имеющие структуры), перечни товаров в электронных таблицах. В структурированных системах поиск осуществляется поэтапно, используя эталонные записи и/или фильтры. В этом же заключается недостаток таких систем, так как они требуют наличия персонала, который сможет классифицировать товар и задать ему первоначальные признаки. Преимущества неструктурированного поиска [4] заключаются в автоматическом выборе системой эталона, в независимости поиска от семантики данных. Однако в противовес такой поиск требует хорошо продуманного алгоритма, учитывающего варианты написания поискового запроса. Это, в свою очередь, добавляет трудностей на этапе внедрения, так как появляется необходимость провести тестирование и определить граничные значения фильтрации, а также значимость каждого из факторов сортировки. Стоит отметить, что такой тип поиска имеет низкую результативность при запросах, содержащих неожиданную для системы терминологию, например различные единицы измерения или сокращения слов, если они не присутствуют в исходной таблице данных.
Целью исследования является разработка системы, осуществляющей автоматический сбор информации с открытых интернет-сервисов для дальнейшей обработки, сохранения, с последующей выдачи в качестве результата на поисковые запросы пользователя. Основу разрабатываемой системы составляют алгоритмы нечёткого поиска.
Материалы и методы исследования
При разработке стратегии поиска был проведён анализ существующих поисковых систем, чтобы определить количество и качество результатов их работы в совокупности со стоимостью технологии [5]. По результатам было определено, что ценность нелинейных (умных) корпоративных поисковых систем обусловлена низким быстродействием или, как правило, высокой ценой. При анализе поисковой системы с точки зрения экономии ресурсов поиск должен быть или быстрым, при сохранении прежнего уровня эффективности, или выгодным для реализации. В любом случае, несмотря на открытость поисковых технологий, чаще всего при разработке используются линейные поисковые алгоритмы, так как этого функционала зачастую достаточно непосредственно заказчику. Однако клиента набор функций поиска обычно не удовлетворяет, что уменьшает привлекательность программного обеспечения.
Большинство алгоритмов поиска имеют зависимость скорости выполнения от количества символов в тексте. Соответственно, использование их для полнотекстового поиска нецелесообразно. Поэтому для увеличения скорости работы алгоритма поиска, предлагается применить прямую индексацию таблиц баз данных, другими словами, необходимо преобразовать оригинальные строки в строки, содержащие только ключевые символы. Для решения этой задачи можно использовать преобразование строк с помощью «метафонов».
Metaphone – это фонетический алгоритм для индексирования слов по их звучанию с учётом основных правил английского произношения, из схожих по звучанию слов получаются одинаковые ключи [6].
Результаты исследования и их обсуждение
Сущность предлагаемого подхода заключается в следующем.
Задачу поиска по неструктурированной информации можно разделить на три этапа и распределить ее по соответствующим подсистемам: 1) обработка входных данных, 2) поиск по индексированным наименованиям, 3) фильтрация по параметрам выходного результата. Подсистема обработки предполагает операции, используемые при индексировании данных: удаление специальных и повторяющихся символов из наименований; формирование слов из чисел и наоборот; разбиение наименований на слова; транслитерация слов с помощью английского алфавита (как международного языка); применение фонетических алгоритмов (метафонов) на строках для получения интерпретации слов; подсчёт количества вхождений слов в наименования; формирование для каждого слова индекса в базе данных системы, который указывает на вхождение в наименование.
Подсистема поиска имеет более интересную функциональную реализацию, чем стандартные линейные методы поиска за счёт использования методов нечёткого поиска (мер схожести).
Практическое использование алгоритмов нечеткого поиска в реальных поисковых системах тесно связано с фонетическими алгоритмами, алгоритмами лексического стемминга – выделения базовой части у различных словоформ одного и того же слова, а также с ранжированием на основе статистической информации, либо же с использованием сложных изощренных метрик [7].
Возможность использовать метрики при обработке данных позволяет получить разницу между начальным запросом и конечным выводом системы. Каждый из существующих алгоритмов поиска задействует собственную метрику, в основном базирующуюся на схожести букв или частей строк с индексированным наименованием. Некоторые алгоритмы и впрямь позволяют назвать численную метрику принадлежностью одной строки к другой (отсюда и название «нечеткий»).
Подсистема поиска первым этапом производит обработку поискового запроса для приведения к общему виду, достаточного для индекса, составляя, таким образом, совокупность из слов. Вторым этапом производится лексический анализ каждого из совокупности слова по базе индексированных наименований посредством меры схожести лексем, формируя нечеткие множества Aj, состоящие из степеней принадлежности индексов к слову.
Нечетким множеством А в некотором (непустом) пространстве X, что обозначается как А ∈ X, называется множество пар A = {(x, μA(X))}, где μA(X) – функция принадлежности нечеткого множества А. Нечеткое множество полностью определяется заданием функции принадлежности μA(X): ее область определения – x ∈ Х, область значений – отрезок [0,1] [8].
Чем выше значение μA(X), тем выше оценивается степень принадлежности элемента x ∈ Х нечеткому множеству А.
Тогда 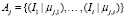 , где j – размер совокупности слов, i – количество индексов, μj,i – значение функции принадлежности j-го слова к i-му индексу. Из множества отсекаются варианты, значения принадлежностей которых не входят в граничные значения алгоритма.
, где j – размер совокупности слов, i – количество индексов, μj,i – значение функции принадлежности j-го слова к i-му индексу. Из множества отсекаются варианты, значения принадлежностей которых не входят в граничные значения алгоритма.
Тем не менее нельзя полагать, что использование одной метрики позволит добиться максимальных результатов. К тому же некоторые метрики можно вычислить быстрее, но они менее надёжны (например, сходство Джаро – Винклера [9]), и, наоборот, некоторые метрики медленнее, но более информативны (расстояние Дамерау – Левенштейна (Задача о расстоянии Дамерау-Левенштейна)). Поэтому для улучшения поисковой релевантности целесообразно использовать несколько мер схожести строк. Это позволяет увеличить быстродействие на этапе поиска данных, отсекая лишние значения выборки, сокращая время на перебор для каждого последующего вычисления метрики.
По завершению анализа всей совокупности формируется итоговое множество, состоящее из пересечений промежуточных множеств, до тех пор пока последующее пересечение не даст пустое множество или не закончится их перебор. Конечным этапом определяются исходные наименования, на которые указывают найденные индексы, составляется нечёткое множество:
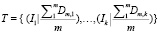 , (1)
, (1)
где k – количество индексов, из которого состоит наименование, Ik – k-й индекс; m – число используемых метрик схожести; Dm,k – нормализированное значение m-й метрики для k-го индекса (относительно граничных значений функции).
Таким образом, определяется, насколько найденные результаты соответствуют поисковому запросу, позволяя гибко распределять их на группы для выполнения последующих операций над ними.
Подсистема фильтрации часто является конечной подсистемой любого поискового алгоритма. Именно на этом этапе сортируются значения в указанном заранее порядке по необходимому критерию (наименованию, цене) и фильтруются при указанном диапазоне входных значений, которые заранее структурированы, например дата, или номер склада (наименование). В случае поиска неструктурированной информации подсистема фильтрации позволяет привести итоговое множество к табличной форме, добавляя один или несколько структурированных критериев (релевантность по метрике) при сортировке, позволяя более гибко получать результаты поиска: вывод в начале релевантных результатов, а затем похожих по написанию или звучанию.
Стратегия поиска в предлагаемой поисковой системе заключается в последовательном переборе определённого количества символов до 20. При этом предполагается, что задача обработки и индексирования данных решена.
Пусть даны две символьные строки: s1 – одна из частей обработанной поисковой строки, s2 – одна из индексированных наименований.
Шаг 1. Вычислять dj(s1, s2) – функцию Джаро – Винклера. Значения функции лежат в интервале [0; 1].
Расстояние Джаро dj между двумя заданными строками s1 и s2 это [9]:
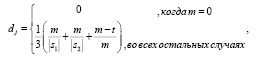 (2)
(2)
где │s1│ – длина строки si ; m – число совпадающих символов; t – половина числа транспозиций.
Каждый символ строки s1 сравнивается со всеми соответствующими ему символами в s2. Количество совпадающих (но отличающихся порядковыми номерами) символов, которое делится на 2, определяет число транспозиций [9].
Расстояние Джаро–Винклера использует коэффициент масштабирования p, что дает более благоприятные рейтинги строкам, которые совпадают друг с другом от начала до определённой длины l, называемой префиксом.
Для двух строк s1 и s2 расстояние Джаро – Винклера dw – это:
dw = dj + (lp(1 – dj)), (3)
где l – длина общего префикса от начала строки до максимума четырех символов; p – постоянный коэффициент масштабирования, использующийся для того, чтобы скорректировать оценку в сторону повышения для выявления наличия общих префиксов. Коэффициент p не должен превышать 0,25, поскольку в противном случае расстояние может стать больше, чем 1. Стандартное значение этой константы в работе Винклера: p = 0,1 [9].
Шаг 2. Выбрать Jcp – некоторое пороговое значение функции Джаро – Винклера для отсеивания лишних результатов, например, 0,75.
Шаг 3. Проверить dw(s1, s2) > Jcp для последующей обработки только похожих вариантов.
Последовательный перебор между поисковым запросом и индексами таблицы работает как линейный поиск, за исключением увеличения сравнивающих операций. Как показали эксперименты, такой метод является достаточно быстрым за счёт небольшого количества операторов функции.
Шаг 4. Получить значение
dL(s1, s2) = d(s1, s2)[|s1|, |s2|]
матрицы рекуррентного соотношения Дамерау – Левенштейна. Значения функции элементов лежат в интервале [0, |si|] . Упрощённо функцию элементов матрицы можно представить следующим образом [10]:
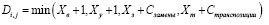 , (4)
, (4)
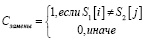 (5)
(5)
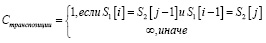 , (6)
, (6)
где i, j – строка и столбец матрицы, используемые для проверки символа первой строки символом второй строки. i, j ∈ [0; max(|s1|, |s2|)]; XВ – необходимое количество вставок символов; XУ – необходимое количество удалений символов; XЗ – необходимое количество замен символов; Xm – необходимое количество транспозиций; XВ, XУ, XЗ, Xm, – число элементов, необходимых для получения исходной строки.
Шаг 5. Выбрать DLcp – некоторое пороговое значение функции Дамерау – Левенштейна для отсеивания лишних результатов, например, 2 (символа).
Шаг 6. Проверять DL(s1, s2) < DLcp для последующей обработки только вариантов с семантическим совпадением.
Последовательный перебор производится между уже отфильтрованными результатами и индексами таблицы, тем самым снижая требования к вычислительной мощности и увеличивая общее быстродействие системы.
Шаг 7. Пусть k – количество структурированных элементов, используемых при сортировке результата (факторы поиска), причем k ≥ 0, а Ck – значение k-го элемента, например, стоимость лекарственного препарата, геопозиция покупателя относительно пункта продаж (аптеки).
Шаг 8. Выполнить нормализацию значений 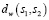 ,
, 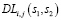 ,
, 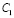 , …,
, …, 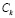 , соответственно получим dw(s1, s2),
, соответственно получим dw(s1, s2), 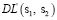 ,
, 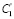 , …,
, …,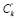 .
.
Шаг 9. Определить количество групп, на которые можно разбить результат, например, «точное совпадение», «возможные варианты» и «альтернативные варианты».
Шаг 10. Сформировать нечёткое множество из нормализованных данных.
В таком случае, функцию принадлежности можно сформировать следующим образом:
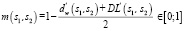 ,(7)
,(7)
где 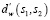 ,
, 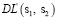 – нормализированные значения самих функций или данных.
– нормализированные значения самих функций или данных.
Инверсия в функции необходима, так как используется расстояние между словами, а не схожесть. При этом усреднение расстояний позволяет добиться большего результата, за счёт того, что оба метода описывают разные метрики, соответственно их объединение добавляет признаки обоих.
Шаг 11. Путём проведения опытов над тестовой совокупностью определить критерии вхождения (пороговые значения) в группы данных. Например, результат с принадлежностью 0.8 может входить в две группы, при этом в группе с точным совпадением он будет иметь меньшую ценность, а в группе с меньшими критериями – большую. Таким образом, это позволит определить качество исходных данных и эффективность поиска. При этом для увеличения результативности будет достаточно поменять критерии вхождения в группу.
Шаг 12. Составить таблицу, состоящую из групп в порядке убывания критериев вхождения (например, сначала будут элементы множества «точные» результаты), добавив столбцы со структурированными данными 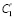 , …,
, …,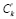 .
.
Шаг 13. Для решения задачи определения релевантности результата воспользуемся кластерным анализом.
Основная задача кластеризации формулируется следующим образом: разделить объекты на группы таким образом, чтобы сходство между объектами одной группы было велико, а сходство между объектами разных групп – мало [11].
В алгоритме уже были выделены характеристики, определены метрики и сделано разбиение на группы. Поэтому можно выделить несколько параметров, описывающих характер объекта:
− μ(s1, s2) – насколько результат соответствует запросу (релевантность);
− C'1, …, C'k – нормализованные значения структурированных данных.
Применив меру близости и правило объединения объектов в кластер на основе имеющихся параметров получим искомые группы. Результат выбора зависит от конечной реализации, так как необходимо определить значимость каждого из факторов и подобрать необходимые группы. Например, за кластер можно принять склады, на которых необходимо найти товар(-ы), тогда структурированными данными будет цена и расстояние до склада.
Шаг 14. На основе значений меры близости отсортировать результат в соответствии с требованиями к алгоритму. При необходимости использовать группировку данных.
Заключение
Таким образом, предлагаемая стратегия поиска по неструктурированным данным предполагает использование фонетических и лингвистических методов обработки данных, а также методов нечёткого поиска. Это позволяет создать поисковую систему, которая учитывает ошибки пользователей, допущенные в результате нажатия неверной клавиши при вводе или в результате фонетической ошибки. Такая система может выдавать не только точные результаты, но и похожие, и, в зависимости от реализации, даже альтернативные варианты. В настоящее время предлагаемый умный алгоритм поиска проходит апробацию в геоинформационной системе поиска лекарственных препаратов с учетом местоположения покупателя. Кроме того, данная стратегия может применяться в глобальных поисковых системах, так как в них большая часть информации не структурирована.
Библиографическая ссылка
Галкин Р.В., Горбачев Д.В., Соловьев Н.А. СТРАТЕГИЯ «УМНОГО» ПОИСКА ДЛЯ ПЕРЕЧНЯ НЕСТРУКТУРИРОВАННЫХ ДАННЫХ // Современные наукоемкие технологии. 2021. № 12-2. С. 211-216;URL: https://top-technologies.ru/ru/article/view?id=38977 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.38977



