В настоящее время четко прослеживается вектор развития индустрии вычислительной техники. С каждым годом вычислительные машины становятся всё более производительными, а их габариты уменьшаются. Вместе с последними экспоненциально растут вычислительные мощности, позволяющие обрабатывать все большие объемы информации. Однако сегодня производители высокопроизводительных вычислительных систем подошли к пределу по закону Мура. Дальнейшее уменьшение размеров транзисторов будет невозможно физически и нецелесообразно экономически. Уже сейчас производители центральных процессорных устройств (ЦПУ) увеличивают производительность за счет увеличения потребляемой энергии и оптимизации в архитектуре. Попытки снизить токопотребление при сохранении высокой производительности приводят к росту числа ошибок в значимых битах регистров ЦПУ и последующему критическому сбою всей системы. Однако алгоритмы, построенные на алгебре гиперразмерных векторов, способны справляться с такими ошибками, так как потеря значимости нескольких бит не влияет на валидность результата вычислений [1]. Данное обстоятельство позволяет создать вычислительное устройство с аппаратной поддержкой алгебры гиперразмерных векторов, которое будет работать на высоких частотах, но с низким токопотреблением, что, в свою очередь, увеличит показатель полезных вычислений на ватт потребленной энергии.
Исходя из вышеописанного, в данной работе представлена разработанная программная инструментальная среда, которая производит симуляцию моделей при помощи алгебры гиперразмерных векторов. Объектом исследования являются алгоритмы кодирования и вычисления состояний автомата при помощи алгебры гиперразмерных векторов. Разработанные алгоритмы позволяют успешно закодировать в вектор любой объект для дальнейших вычислений. Это позволит проектировать эвристические системы на базе нейросети, которая сможет принимать любые данные для вычислений, закодированные в гиперразмерный вектор, что решает проблему позиционирования данных [2].
Материалы и методы исследования
В качестве способа кодирования целевых систем используется автоматная модель. Абстрактные автоматы – вычислительные машины, представленные в виде математических моделей, осуществляющие обработку информации по заданному алгоритму [3–6]. Самым распространённым способом представления абстрактных автоматов является графический способ. Автомат представляется как граф, где вершинами представляются все возможные состояния автомата, а стрелками – переходы между состояниями [7, 8]. В качестве примера графического представления автомата на рис. 1 продемонстрирован граф автомата D-триггера.
Разработанная инструментальная программная система позволяет моделировать системы путем кодирования в виде абстрактного автомата. В отличие от большинства существующих решений, инструментальная система моделирования представляет целевую систему в векторно-символьной архитектуре.
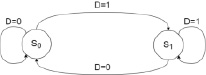
Рис. 1. Графическое представление работы D-триггера
Гиперразмерный вектор представляет собой двоичный вектор высокой размерности, который содержит случайную последовательность нулей и единиц, полученную с использованием равномерного закона распределения. Основной метрикой, которая используется при сравнении двух гиперразмерных векторов, является расстояние Хэмминга. Считается, что два гиперразмерных вектора не пересекаются, если расстояние Хэмминга ≥ 0,5. Если расстояние Хэмминга < 0,5, то это говорит о том, что сравниваемый HD-вектор входит в результирующий.
Для симуляции поведения целевой системы в программе используются операции алгебры гиперразмерных векторов, такие как сложение векторов, умножение векторов, очищение результирующего вектора от шума. Одним из преимуществ использования векторно-символьной архитектуры является оптимальная алгоритмическая сложность вычисления активных состояний при представлении целевой системы в формате недетерминированного автомата.
Возможность представлять все активные состояния автомата одним гиперразмерным вектором описывается свойствами алгебры гиперразмерных векторов.
Описание элементов интерфейса
Интерфейс программы состоит из окна ввода блока управления, окна ввода системы канонических уравнений и окна симуляции, где отображается граф автомата целевой системы [9, 10]. Окно программы продемонстрировано на рис. 2.
Блок управления программой состоит из следующих кнопок:
1) кнопка сохранения закодированной целевой системы в файл;
2) кнопка загрузки целевой системы из файла;
3) кнопка запуска кодирования системы уравнений в граф автомата;
4) таблица сигналов для установки их значений.
На рис. 3 продемонстрирован блок кнопок управления программой.
Рис. 2. Окно системы моделирования систем

Рис. 3. Кнопки управления программой
Блок управления симуляцией состоит из следующих кнопок:
1) кнопка запуска симуляции;
2) кнопка пошаговой симуляции;
3) кнопка остановки симуляции, если симуляция была запущена по кнопке 1;
4) кнопка сброса системы в исходное состояние.
На рис. 4 продемонстрирован блок кнопок управления симуляцией

Рис. 4. Кнопки управления симуляцией
Описание и демонстрация работы среды моделирования
Были разработаны алгоритмы кодирования целевой системы путём парсинга системы канонических уравнений (СКУ) [11, 12]. СКУ задаются как набор формул в нормальной дизъюнктивной форме (ДНФ). В качестве операндов самого уравнения выступают конъюнкты, состоящие из предыдущего состояния и выходного сигнала предыдущего состояния, само же уравнение приравнивается к новому состоянию. Количество конъюнктов определяет количество вершин графа автомата, из которых осуществляется переход.
После ввода СКУ пользователем происходит кодирование в векторно-символьную архитектуру. Для каждого состояния Si и сигнала Xi генерируются случайные гиперразмерные вектора, далее происходит расчет вектора всего автомата А по формуле (1). При этом операции конъюнкции и дизъюнкции заменяются на операции умножения и сложения соответственно. Для кодирования однонаправленного перехода из первоначального состояния в следующее в представлении векторно-символьной архитектуры, используется операция циклического битового сдвига вправо, обозначенного в формулах как функция sr(V, n), где V – входной n – количество бит, на которое сдвигается входной вектор V.
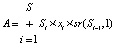 . (1)
. (1)
После завершения кодирования пользователь может начать пошаговую симуляцию. Причем вычисления происходят исключительно с HD-векторами сигналов и состояний автомата. Вычисление следующего состояния системы производится по формуле
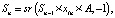 (2)
(2)
Sn – следующее состояние автомата;
Sn–1 – предыдущее состояние автомата;
xin – входной сигнал, по которому автомат переходит в состояние Sn.
Для вычисления следующих активных состояний на шаге симуляции при представлении целевой системы в виде недетерминированного автомата, используется формула (3). Здесь и в дальнейших формулах используется знак приближения, поскольку в действительности будет получена сумма, содержащая помимо векторов частных состояний автомата, образующих вектор очередного обобщенного состояния недетерминированного конечного автомата, также ряд векторов, представляющих собой шум, т.е. векторы, неподобные ни к одному из векторов частных состояний или входных сигналов автомата.
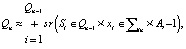 (3)
(3)
Qn – результирующий вектор с активными состояниями;
Qn–1 – множество предыдущих состояний автомата;
Si – предыдущее состояние;
xi – входной сигнал, по которому автомат переходит в состояние 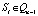 .
.
∑in – множество входных сигналов, при которых недетерминированный автомат входит в активные состояния Qn.
Для демонстрации взаимодействия пользователя с системой на рис. 5 представлена UML-диаграмма последовательности.
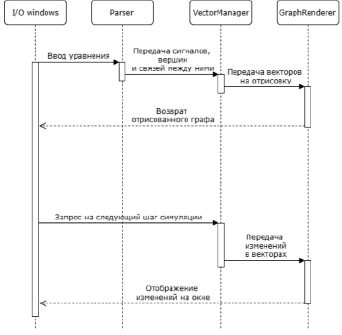
Рис. 5. Диаграмма последовательности работы системы
Для демонстрации вычислений в векторно-символьной архитектуре, в качестве примера опишем абстрактную информационную систему в виде графа, продемонстрированного на рис. 6.
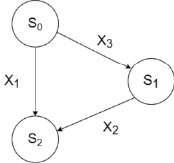
Рис. 6. Граф автомата системы
Граф целевой информационной системы можно представить в виде СКУ, описанной формулами
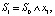 (4)
(4)
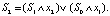 (5)
(5)
После трансформации в векторно-символьную архитектуру у нас выходит следящая СКУ, представленная формулами
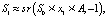 (6)
(6)
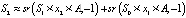 . (7)
. (7)
Но для симуляции необходимо найти вектор всего автомата A, вычисляемый по формуле
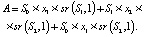 (8)
(8)
После ввода уравнения в систему и кодирования в векторно-символьную архитектуру, программа вывела граф, продемонстрированный на рис. 7.
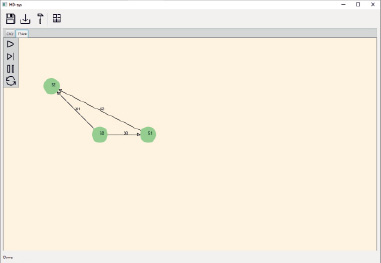
Рис. 7. Граф автомата системы в программе
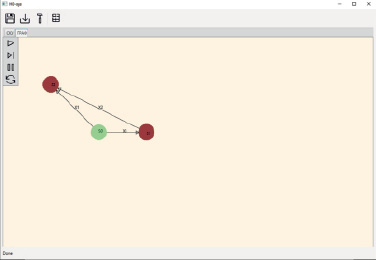
Рис. 8. Симуляция системы на шаге 2
После установки для всех сигналов значения 1, запускается пошаговая симуляция. После перехода из активного состояния S0, автомат перешел в сразу несколько активных состояний S1 и S2. Развернутый расчет следующих активных состояний автомата представлен по формуле
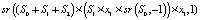 +
+
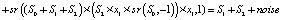 . (9)
. (9)
Результат перехода продемонстрирован на рис. 8.
Следующий шаг симуляции перевел автомат в состояние S2, после чего симуляция завершилась. Последний шаг симуляции продемонстрирован на рис. 9.
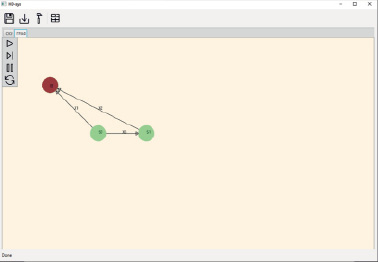
Рис. 9. Симуляция системы на последнем шаге
Выводы
Разработанная программная инструментальная среда моделирования позволяют решить задачу моделирования комплексных систем в виде недетерминированного конечного автомата с множеством состояний. В рассмотренном примере представлена простейшая автоматная модель, позволяющая проследить процесс гиперразмерных вычислений в ходе формирования результирующего вектора. Для реальных практических задач, в которых соответствующие недетерминированные автоматные модели имеют тысячи и десятки тысяч состояний, переходы между которыми идут параллельно, возникает проблема высоких вычислительных затрат.
Предложенный в работе метод моделирования процессов переходов для недетерминированного конечного автомата за счет избыточности представления позволит в будущем применять аппаратные решения, обладающие высоким уровнем параллелизма и быстродействия, но при этом некоторой долей ошибок вычислений без внедрения дополнительных методов их коррекции.
Таким образом, развитие теории гиперразмерных вычислений со временем обеспечит возможность перехода к принципиально иным уровням быстродействия вычислительных устройств.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-07-00516 А.
Библиографическая ссылка
Мартышкин А.И., Трокоз Д.А., Пащенко Д.В., Калашников В.А., Синев М.П. ПРОЕКТИРОВАНИЕ ИНСТРУМЕНТАЛЬНОЙ ПРОГРАММНОЙ СИСТЕМЫ ПОДДЕРЖКИ МЕТОДОЛОГИИ ПРОЕКТИРОВАНИЯ СЛОЖНЫХ СИСТЕМ НА ОСНОВЕ АВТОМАТНЫХ МОДЕЛЕЙ С ИСПОЛЬЗОВАНИЕМ АЛГЕБРЫ ГИПЕРРАЗМЕРНЫХ ВЕКТОРОВ // Современные наукоемкие технологии. 2021. № 12-1. С. 60-66;URL: https://top-technologies.ru/ru/article/view?id=38955 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/snt.38955



