Векторное представление (векторизация) слов – представление слова в виде цифрового объекта в векторном пространстве – важнейший элемент при решении задач обработки естественного языка (Natural Language Processing, NLP). Главная парадигма такого представления зародилась на принципах дескриптивного направления структурной лингвистики, впервые сформулированных Л. Блумфилдом в 1920-х гг. Позднее на их основе З. Харрисом была сформулирована дистрибутивная гипотеза, основанная на идее, что слова, окруженные похожим контекстом, имеют схожее значение. Основываясь на дистрибутивной гипотезе, были получены различные варианты векторных представлений слов. Некоторые исследователи группировали слова в кластеры в зависимости от их контекста, другие – представляли слова в виде сильно разреженных векторов очень большой размерности, в которых каждый элемент представлял собой степень связи слова с определенным контекстом [1]. Для уменьшения размерности разреженных векторов затем использовались различные математические методы, такие как сингулярное разложение (Singular Value Decomposition, SVD [2]) или латентное размещение Дирихле (Latent Dirichlet Allocation, LDA [3]). В начале XXI в. было предложено представлять слова в виде плотных векторов, полученных при помощи различных моделей нейронных сетей [4, 5], которые неплохо себя зарекомендовали для решения различных задач компьютерной лингвистики [6–8]. Среди методов векторного представления слов, основанных на моделях искусственных нейронных сетей, наибольшее распространение получили два алгоритма машинного обучения: CBoW (Continuous Bag of Words) и Skip-gram [5], реализованных в утилите wod2vec группой исследователей Google в 2013 г. CBoW предсказывает слово исходя из окружающего его контекста, а Skip-gram предсказывает контекст исходя из текущего слова. Таким образом, выделяют четыре принципиальных подхода к векторизации слов. Первый – это классический подход «мешка слов» (bag-of-words), в котором текст представляется как множество слов, игнорируя грамматику и даже порядок слов в тексте. Этот подход успешно используется при решении задачи классификации текстов. Второй – это тематическое моделирование, упомянутое выше [2], основанное на латентном размещении Дирихле. Третий подход основан на нейронально-вероятностных языковых моделях, оценивающих функцию вероятностей совместной встречаемости слов в языке. В связи с высокой размерностью таких моделей, они, как правило, реализуются в виде n-грамм – объединения очень коротких перекрывающихся последовательностей, наблюдаемых в обучающем наборе. Этот подход, в сущности, реализован в утилите word2vec. И, наконец, четвертый подход получает в настоящее время наибольшее распространение благодаря огромному росту моделей нейронных сетей. Он основан на неконтролируемом обучении с учителем на основе больших библиотек входных данных, используя различные нелинейные многослойные операторы. В данной работе реализуется именно этот подход. В качестве модели нейронной сети используется сверточная нейронная сеть, хорошо зарекомендовавшая себя в задачах компьютерного зрения. В отличие от рекуррентных нейронных сетей, которые в последнее время получили наибольшее распространение в задачах векторного представления слов, в сверточных нейронных сетях используется нелинейное представление исходных данных. В связи с этим целью данной работы является построение модели сверточного автокодировщика для векторного представления слов русского языка. Для того чтобы обучить модель сверточного автокодировщика, необходимо представить слова в виде двумерного массива. Нами предложено три варианта такого представления и проведено их сравнение. Разработаны пять различных моделей архитектуры сверточной нейронной сети. Проведена оптимизация гиперпараметров и опций нейронной сети, таких как размер партии (batch size) и размер ядра (kernel size).
Автокодировщик (автоэнкодер, autoencoder) – модель нейронной сети, для которой количество нейронов на входном и выходном слое одинаковое. Основная задача автоэнкодера получить как можно меньшее количество нейронов на скрытом слое, при этом сохранить максимальную близость значений входного и выходного слоя. Структурно автоэнкодер состоит из энкодера и декодера. Энкодер преобразует входной сигнал в набор весов скрытого слоя (ai), размерность которого значительно меньше размера входного слоя (xj). Декодер восстанавливает исходный сигнал (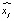 ) из элементов скрытого слоя (ai). При этом ошибка восстановления (реконструкции) сигнала
) из элементов скрытого слоя (ai). При этом ошибка восстановления (реконструкции) сигнала 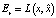 , являющаяся функцией различий входного и выходного слоя, и число нейронов скрытого слоя Lv являются основными параметрами, относительно которых происходит оптимизация нейронной сети.
, являющаяся функцией различий входного и выходного слоя, и число нейронов скрытого слоя Lv являются основными параметрами, относительно которых происходит оптимизация нейронной сети.
Задача автоэнкодера состоит не столько в уменьшении размерности представления данных, сколько в поиске некоторых закономерностей в них. В связи с этим автокодировщик строится в предположении наличия некоторых закономерностей в исходном сигнале. Если бы исходный набор состоял из признаков, которые были бы независимы один от другого, то задача сжатия и реконструкции исходных данных была бы крайне сложной. В целом задача энкодера в большой степени схожа с задачей классического статистического метода главных компонент (Principal component analysis, PCA) и идентична ей в случае, если исключить из каждого слоя нелинейную функцию активации. Различие состоит в том, что метод главных компонент пытается обнаружить низкоразмерную гиперплоскость, которая описывает исходные данные, в то время как автоэнкодеры ведут поиск зависимостей в виде нелинейных многообразий, то есть непрерывных непересекающихся поверхностей.
Основной задачей данного исследования является сжатие исходного представления слова до вектора как можно меньшей длины (обозначим Lv, vector length) при условии минимизации ошибок при восстановлении слова из полученного вектора (обозначим Er, recovery error). Для проверки работы нейронной сети имеющийся словарь, состоящий из 6 807 724 слов, был разделен на обучающую и тестовую выборки в соотношении 90 % и 10 % соответственно.
Материалы и методы исследования
В настоящей работы были использованы модели сверточных нейронных сетей (Convolutional Neural Networks, CNNs, ConvNets), которые показали себя достаточно успешно в задачах классификации изображений [9]. Основная идея сверточной нейронной сети состоит в том, что каждый нейрон сверточного слоя связан только с частью соседних нейронов входного слоя, размер этой части называется размером ядра свертки (kernel size, receptive field) и двигается по входному слою с некоторым шагом (stride). Необходимость иметь целое число нейронов на выходе после сверточного слоя реализуется в добавлении к граничным точкам входного слоя определенного количества нулей (zero-padding). Практически это означает целочисленный результат вычислений по формуле
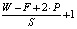 ,
,
где W – размер входного слоя, F – размер ядра, P – размер заполненного нулями приграничного пространства, S – шаг, на который смещается ядро свертки.
Как правило, сверточные нейронные сети применяются к анализу изображений, представляющих собой трехмерную матрицу, имеющую ширину и высоту (размер изображения в пикселях), а также глубину, размер которой равен 3 (по числу каналов в цветовой модели RGB). В связи с этим для применения сверточной нейронной сети к текстовым данным необходимо решить задачу представления слов в матричном виде. Предложены и апробированы 3 варианта матричного представления слов.
В первом варианте матричное представление слова реализуется с использованием порядка буквы слова в алфавите и самом кодируемом слове. К основному алфавиту добавлен дефис, а также цифры 0 и 1. Таким образом, слово представлено в виде матрицы размером 36×36, состоящей из 1296 нулей и единиц.
Второй подход для матричного представления слова основан на кодировке букв алфавита в виде шестимерного вектора в двоичной системе счисления. В этой кодировке помимо букв русского алфавита добавлены дефис, пробел, цифра ноль, а также метка концы слова, состоящая из шести нулей. При таком варианте слово представлялось в виде матрицы размером 28×6, состоящей из 168 нулей и единиц.
Недостатком первого и второго подхода является ограниченность их использования только русским алфавитом. При этом расширение алфавита в первом подходе приведет к колоссальному росту числа элементов матрицы. В связи с этим необходимость добавления других алфавитов может быть удовлетворена за счет модификации второго подхода. Идея представления слова остается той же, только вместо шестимерного двоичного вектора используется вектор большей размерности. Чтобы придать данной кодировке большую универсальность, берется код символа в системе UNICODE и переводится из шестнадцатеричной системы счисления в двоичную. В результате такого представления слово кодируется матрицей размера 28×16, состоящей из 448 нулей и единиц.
В общем виде модель нейронной сети выглядит следующим образом:
Y = f(W∙X + B),
где X – входной сигнал на текущий слой нейронной сети, f – функция активации, Y – выходной сигнал со слоя нейронной сети, W и B – параметры нейронной сети, точкой обозначено скалярное умножение. Обучение нейронной сети, по сути, сводится к подбору параметров, минимизирующих значение функции ошибок. Как правило, для оптимизации параметров используется метод стохастического градиентного спуска. Суть его состоит в том, что после каждой итерации значения параметром изменяют на некоторую величину в направлении, противоположном градиенту функции ошибок. В качестве функции ошибок (loss function) была выбрана бинарная кросс-энтропия (binary crossentropy), вычисляемая по формуле
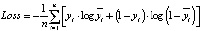 ,
,
где n – число нейронов выходного слоя, 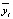 – нейроны выходного слоя модели, yi – точные значения.
– нейроны выходного слоя модели, yi – точные значения.
При обучении весь набор данных делится на партии. Размер такой партии (batch size) влияет на качество и скорость обучения. Завершенный процесс, когда весь набор данных один раз прошел через нейронную сеть, называется эпохой (epoch). Кроме того, в случае сверточной нейронной сети на качество и скорость модели влияет также размер ядра свертки. Все эти и многие другие значения, влияющие на процесс подбора параметров сети, называют гиперпараметрами, то есть гиперпараметры – это «параметры, управляющие параметрами».
Словарь для обучения нейронной сети для векторизаци слов, используемый в настоящей работе, состоит из более чем 6,8 млн слов. В связи с этим для обучения нейронной сети даже за одну эпоху требуются большие затраты машинной памяти. Поэтому была разработана функция, оптимизирующая обучение нейронной сети с точки зрения затрат машинной памяти и времени обучения – генератор партий (batch generator). Данный генератор загружает заранее подготовленные данные и по частям отправляет их в нейронную сеть. Y – это массив имён файлов, состоящих из заранее подготовленных данных. Как только один из элементов Y пройдёт обучение, то память очищается и загружается следующий элемент списка. Использование данного механизма позволяет в разумные сроки производить обучение рассмотренных выше моделей нейронных сетей.
Результаты исследования и их обсуждение
В работе были построены несколько вариантов автокодировщиков в зависимости от структуры, содержания и количества слоев нейронной сети, а также от формы матричного представления исходных данных. Наиболее удачными оказались 5 вариантов моделей.
Модель I. Энкодер данной модели состоит из входного слоя, использующего первый тип матричного представления слоя, линеаризующего слоя Flatten, в котором происходит простая стыковка строк входной матрицы в линейный вектор, а также полносвязного слоя Dense. Декодер данной модели также содержит полносвязный слой и разворачивает полученный вектор обратно в матрицу при помощи функции Reshape.
Сеть была обучена на словаре, состоящем из 350 000 слов. Процент ошибок на тренировочных данных Er = 0.086 %, на тестовых данных Er = 0.611 %. Длина вектора представления слова после энкодера Lv = 72.
Модель II. Данная модель представляет собой, собственно, сверточный автоэнкодер. Энкодер состоит из входного слоя, использующего первый тип матричного представления слова и троекратного последовательного применения сверточного слоя (convolution layers) и слоя подвыборки (субдискретизирующий слой, subsampling layers, pooling layers). Ядро сверточного слоя имеет размер 3×3. Размер фильтра для слоя подвыборки 2×2, шаг равен 2. В качестве функции для слоя подвыборки использована функция максимума. Суть слоя подвыборки состоит в уплотнении нейронов предыдущего слоя сети. В данном случае в каждом неперекрывающемся квадрате 2×2 матрицы, полученной с предыдущего слоя, выбирался наибольший элемент. Декодер модели практически симметричен энкодеру, за исключением замены слоя подвыборки, понижающего дискретность данных, слоем, повышающим эту дискретность (upsampling). Повышение дискретности изображения происходит простым дублированием каждого элемента предыдущего слоя до матрицы размера 2×2. Сеть была обучена на словаре, состоящем из 300 000 слов. Процент ошибок на тренировочных данных Er = 0,042 %, на тестовых данных Er = 0,263 %. Длина вектора представления слова после энкодера Lv = 800.
Модель III. Энкодер данной модели использует на входном слое второй тип матричного представления слова. Далее осуществляется непосредственно свертка (Conv2D), функция активации ReLU (Rectified Linear Unit), слой нормализации (BatchNormalization), линеаризирующий слой (Flatten) и полносвязный слой (Danse). Слой Leaky ReLU (выпрямитель с «утечкой») реализует пороговый переход в нуле, данная функция активации задается формулой 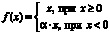 . В качестве параметра α выбрано значение 0,2. Слой нормализации производит центрирование и нормирование данных, поступающих с предыдущего слоя, а затем их линейное преобразование по формулам
. В качестве параметра α выбрано значение 0,2. Слой нормализации производит центрирование и нормирование данных, поступающих с предыдущего слоя, а затем их линейное преобразование по формулам
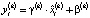 ,
,
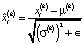 ,
,
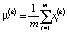 ,
,
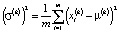 ,
,
где 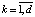 , d – размерность данных, ∈ – сколь угодно малая константа, обеспечивающая численную устойчивость, m – число элементов слоя, параметры γ(k) и β(k) обучаются итерационно в процессе оптимизации сети.
, d – размерность данных, ∈ – сколь угодно малая константа, обеспечивающая численную устойчивость, m – число элементов слоя, параметры γ(k) и β(k) обучаются итерационно в процессе оптимизации сети.
Декодер состоит из полносвязного слоя, слоя развертки в матрицу (Reshape), обратного сверточного слоя (Conv2DTranspose), функции активации LeakyReLU, слоя нормализации (BatchNormalization), еще одного обратного сверточного слоя и функции активации «сигмоида», возвращающей данные в диапазон [0, 1] для восстановления слова. Сигмоида задается формулой 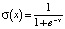 и характеризуется тем, что переводит значения в диапазон [0, 1]. Сеть была обучена на словаре, состоящем из 6 807 710 слов. Процент ошибок на тренировочных данных Er = 0 %. Длина вектора представления слова после энкодера Lv = 72.
и характеризуется тем, что переводит значения в диапазон [0, 1]. Сеть была обучена на словаре, состоящем из 6 807 710 слов. Процент ошибок на тренировочных данных Er = 0 %. Длина вектора представления слова после энкодера Lv = 72.
Модель IV. Данная модель на входном слое использует второй тип матричного представления слова. Далее идет сверточный слой, свертка происходит только по одной оси (Conv1D) – по номеру буквы в слове, функция активации Leaky ReLU, нормализация, линеаризация и полносвязный слой. Декодер состоит из входного слоя, полносвязного слоя, слоя развертки вектора в матрицу, свертки по одной оси, активации LeakyReLU, нормализации, еще одной одномерной свертки. Завершается декодер функцией активации сигмоида, переводящей значения в диапазон [0, 1] для восстановления слова. Сеть была обучена на словаре, состоящем из 2 414 871 слов. Процент ошибок на тренировочных данных Er = 0,000 %, на тестовых данных Er = 0,022 %. Длина вектора представления слова после энкодера Lv = 96.
Модель V. Энкодер данной модели на входном слое использует третий подход матричного представления слов. Он состоит из свертки по двум осям (Conv2D), функции активации LeakyReLU, нормализации, линеаризации и полносвязного слоя. Декодер представлен полносвязным слоем, слоем развертки вектора в матрицу, обратной свертки, функции активации LeakyReLU, нормализации, еще одной обратной свертки. Завершается декодер функцией активации сигмоида, переводящей значения в диапазон [0, 1] для восстановления слова. Сеть была обучена на словаре, состоящем из 6 807 726 слов. Процент ошибок на тренировочных данных Er = 0,000 %. Длина вектора представления слова после энкодера Lv = 128.
Как уже было сказано выше, размер партии влияет на качество и скорость обучения моделей нейронных сетей. В связи с этим было проведено сравнение моделей с разными значениями этих гиперпараметров. Для Модели II график зависимости потерь (binary crossentropy) от количества эпох приведен на рис. 1. Для Модели II, использующей первый вариант представления слова в виде матрицы размером 36×36, наилучшим значением параметра batch size оказалось 256.
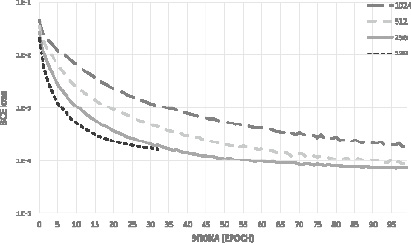
Рис. 1. Модель II нейронной сети с разным числом партий
Для Модели III график зависимости потерь (loss) от количества эпох приведен на рис. 2. Наилучший размер партии для этой модели, использующей второй вариант представления слова в виде матрицы 28×6 – 1024.
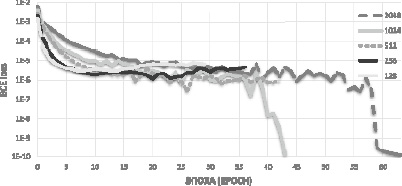
Рис. 2. Модель III нейронной сети с разным числом партий
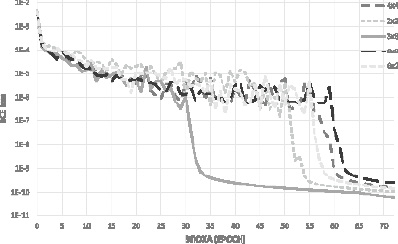
Рис. 3. Модели III нейронной сети в зависимости от размера ядра свертки
Оптимизация гиперпараметра сверточной нейронной сети – размер ядра свертки проводилась с точки зрения точности и скорости обучения. Скорость обучения рассматривалась с двух различных позиций: непосредственно затраченного машинного времени и количества эпох для достижения максимальной точности. Для Модели III нейронной сети брали в качестве размера ядра 3 варианта квадратной матрица (2×2, 3×3, 4×4) и 3 варианта прямоугольной матрицы (6×2, 2×6, 6×3). Выбор размера прямоугольного ядра обусловлен вторым типом представления слова в виде матрицы размером 28×6. Наилучшие результаты были получены для размеров ядра 6×3 и 2×2. Результаты представлены на рис. 3.
Аналогичные исследования проведены для модели V. В качестве размера ядра были выбраны 3 тех же самых варианта квадратной матрицы (2×2, 3×3, 4×4) и 2 варианта прямоугольной (16×2 и 16×3). Результаты представлены на рис. 4. Лучшей оказалась модель с размером ядра свертки 3×3.
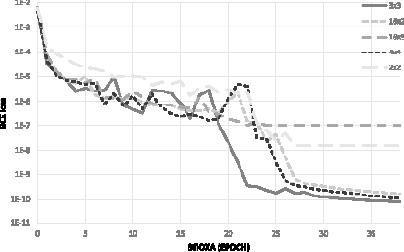
Рис. 4. Модели V нейронной сети в зависимости от размера ядра свертки
Сводные гиперпараметры моделей и результаты обучения
|
Модель |
Размер партии |
Размер ядра свертки |
Размер словаря для обучения |
Размер вектора после энкодера |
Процент ошибок на обучающей выборке |
Процент ошибок на тестовой выборке |
Число эпох |
Время обучения |
Функция активации |
Функция ошибок |
Размер входной матрицы |
|
I |
1024 |
– |
350 000 |
96 |
0.086 % |
0.611 % |
369 |
0:22:47 |
relu |
binary crossentropy |
36×36 |
|
II |
256 |
3×3 |
300 000 |
(5,5,32) |
0.265 % |
0.289 % |
100 |
1:07:47 |
relu |
binary crossentropy |
36×36 |
|
III |
1024 |
3×3 |
6 807 710 |
72 |
0.000 % |
– |
44 |
1:09:28 |
LeakyReLU |
binary crossentropy |
28×6 |
|
IV |
1024 |
3 |
2 414 871 |
96 |
0.000 % |
0.022 % |
96 |
2:03:47 |
LeakyReLU |
binary crossentropy |
6×28 |
|
V |
1024 |
3×3 |
6 807 726 |
128 |
0.000 % |
– |
39 |
2:47:11 |
LeakyReLU |
binary crossentropy |
28×16 |
Заключение
Задача векторизации слов является ключевым этапом создания интеллектуальных автоматических систем взаимодействия с пользователем. С использованием нейросетевых моделей удалось решить эту задачу с приемлемой точностью. Построив более 50 различных моделей автокодировщиков на основе искусственных нейронных сетей, было выбрано 5 моделей, приведенных выше, которые используют разные типы архитектуры нейронных сетей и разные способы представления входных данных в виде матрицы. Проведена оптимизация гиперпараметров сети batch size и kernel size, а также разработан механизм, позволяющий обучать большие словари данных (batch generator). Сводные результаты моделей приведены в таблице.
Наиболее универсальной является Модель V, использующая UNICOD, для кодировки символов и позволяющая расширить данную модель на многоязычные тексты. Кроме того, в данной модели кодируются не только буквы национальных алфавитов, но и знаки препинания, специальные символы и др. Обучение данной модели на всем словаре, состоящем из более чем 6,8 млн слов, заняло чуть менее трех часов машинного времени. При этом все слова после декодирования восстанавливаются без ошибок. Размер вектора представления слова равен 128. Следующим этапом в решении глобальной задачи создания системы взаимодействия с пользователем является векторизация предложения. В качестве матричного представления предложений может быть использован вектор слова после энкодера. Таким образом, матричное представление предложений для обучения автокодировщика будет иметь размерность m×28, где m – максимальное число слов в предложении.
Библиографическая ссылка
Лихачев А.Ю., Трубянов А.Б. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ СЛОВ РУССКОГО ЯЗЫКА ПОСРЕДСТВОМ НЕЙРОСЕТЕВЫХ МОДЕЛЕЙ СВЕРТОЧНОГО АВТОЭНКОДЕРА // Современные наукоемкие технологии. 2021. № 12-1. С. 52-59;URL: https://top-technologies.ru/ru/article/view?id=38954 (дата обращения: 03.01.2026).
DOI: https://doi.org/10.17513/snt.38954



