Основная проблема при записи сигналов ЭКГ и других биопотенциалов заключается в том, что сигнал измерения искажается дополнительными помехами от линии электропередачи (ПЛП). Хорошо известный метод, позволяющий уменьшить такие помехи, заключается в использовании режекторного (ФР) или многорезонаторного фильтра, характеризующегося единичным усилением на всех частотах, за исключением режекторных частот, где усиление равно нулю. Если частота помех от линии электропередачи известна заранее, можно использовать фиксированные режекторные, полосо-заградительные (ПЗФ) фильтры [1]. Однако, когда эта частота неизвестна или изменяется во времени, применимы адаптивные режекторные фильтры [2].
Цель проекта – разработка цифрового режекторного фильтра, который включает в себя быстрое преобразование Фурье (БПФ) сигнала, обнуление коэффициентов Фурье при/около 50 Гц (лучше всего использовать пологие наклоны, чтобы минимизировать появление артефактов, возникающих в результате острых краев), а затем использование обратного БПФ [3].
Материалы и методы исследования
Цифровые фильтры были реализованы на языке Python 3 c библиотекой MatLab. Входным сигналом был нефильтрованный сигнал с платы сбора данных (x[n]). Фильтры БИХ были реализованы на основе двухполюсной функции передачи с двумя нулевыми отметками, по одной для каждой отклоненной частоты [4, c. 584]. Коэффициенты фильтра БИХ были рассчитаны с помощью метода билинейного преобразования по отклику Чебышева второго порядка с требуемой добротностью. При этом фильтры КИХ, или фильтры всех нулей, были решены на основе линейно-фазовой выемки высокого порядка (n = 199), также по одному для каждой отклоненной частоты. Коэффициенты фильтра КИХ были рассчитаны на основе алгоритма Ремеза для достижения желаемого отклика на выемку. В процедурах реализации алгоритмов фильтрации сначала ЭКГ-сигнал из базы данных загружается на платформу Python. Затем шумовой сигнал добавляется к загруженному ЭКГ. Для проекта была взята 25-секундная запись с лабораторных неинвазивных электрокардиограмм, которая отбиралась со скоростью 360 Гц и разрешением 16 бит, а затем была сокращена с 9000 до 213 = 8192 выборок. Шумовой сигнал частотой 0,25 Гц был сгенерирован в среде Python, а затем добавлен в исходную базу данных ЭКГ и в дальнейшем исследуются соответствующие параметры конструкции для различных цифровых фильтров [5, c. 256].
Для программной реализации используют функцию lfilter (signal.lfilter(b, a, tx, zi = z). Следующее выражение дает передаточную функцию цифрового ФР 2-го порядка [6]:
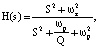
где wz относится к нулевой круговой частоте, в то время как wp – к полярной круговой частоте, Q – коэффициент качества режекторного фильтра. Q = fr / Bandwidth. Частота среза ФР: нижняя: fL = 1 / 2πRLC, высокая: fH = 1 / 2πRHC. Рассмотрим цифровой режекторный фильтр Чебышева четвертого порядка с частотой дискретизации 360Hz и частотой отсечения 45Hz. Полосовой фильтр был разработан с использованием двух нулей, расположенных на ±jw0. Эти типы конструкций не имеют единичного усиления на нулевой частоте [7]. Режекторный фильтр можно разработать, поставив два полюса рядом с нулями. Теорема выборки Найквиста – Шеннона определяет, что все нормализованные частоты будут находиться в интервале [0, π].
f0 = 50 Гц, fc = 45 Гц, fs = 360 Гц,
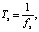
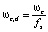≈ 0.7854 рад/с.
В общем случае фильтрация сигнала приводит к задержке, при этом фильтры БИХ задерживают некоторые частотные составляющие больше, чем другие. Функция filtfilt компенсирует задержки, вносимые такими фильтрами, и, таким образом, корректирует искажения фильтра. Эта «фильтрация нулевой фазы» является результатом фильтрации сигнала в прямом и обратном направлениях. Угловая частота лежит рядом с 45Hz, где A(ωc,d) = -3.01dB (рис. 5, в). В соотношение полюсной частоты ω0 и нулевой частоты.
Если нулевая частота равна полюсной частоте, то получается стандартный вырез. Ширина полосы пропускания коррелируется с положением полюсов. Узкая полоса пропускания привела к тому, что полюса удаляются от центра единичного круга, и наоборот (рис. 1, а). Узкая полоса пропускания режекторного фильтра обеспечивала идеальную фильтрацию только на частоте 50 Гц (рис. 1, б). Предполагая, что есть два фильтра h1 и h2, мы вводим выход h1 в h2, и полученный фильтр будет компоноваться каскадом h1 и h2. Импульсная характеристика каскадного фильтра является сверткой импульсной характеристики h1 и h2, а его частотная характеристика является произведением частотной характеристики двух фильтров. Проектируем КИХ ФР по алгоритму Ремеза с частотой режекции wn = 0,6 π и ω0 = 0,55 π, ω1 = 0,65 π.
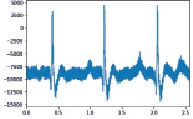
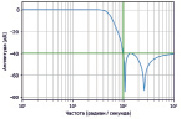
а) б)
Рис. 1. а. Сигнал ЭКГ с шумом ПЛП; б. АЧХ и ФЧХ полосового фильтра, n = 4
При этом, чтобы получить характеристики надреза, помещаем одну сложную пару нулей на единичный круг. Сначала рассчитывается нормированная частота ωc,d:
fs = 360 Гц, fc = 50 Гц,
ωс = 2πfc ≈ 314.2 рад с–1,
Первый шаг – это нахождение быстрого преобразования Фурье (БПФ) ЭКГ-сигнала (рис. 2, а). На основе информации, полученной путем построения БПФ сигнала ЭКГ в частотной области, разрабатывается два типа цифровых фильтров. Первая конструкция фильтра – это ФР КИХ и соответствующий, БИХ-фильтр.
w, h = freqz(b, a) # Вычислить частотную характеристику
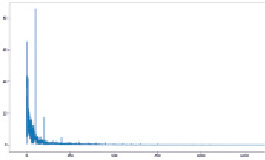
а)
б)
Рис. 2. а. График БПФ; б. Частотно-амплитудные характеристики
Из частотной характеристики фильтра Чебышева 2 можно сделать следующие наблюдения (рис. 2, б): а) разработанный фильтр соответствует этим требованиям; б) полоса пропускания – плоская. Значение меньше нуля, указывающее на запаздывающую фазу; в) полоса остановки характеризуется наличием ряби, каждая из которых имеет одинаковую интенсивность; г) фазовая характеристика приблизительно линейна для частот нижней полосы пропускания. Импульсные отклики затухают со временем, т.е. фильтр стабилен. Это подтверждается диаграммами полюс-ноль, на которых все полюса находятся в пределах единичного круга. Диаграммы polezero также содержат нули, расположенные на единичном круге.
Алгоритм Ремеза (Паркса – Макклеллана)
Алгоритм Ремеза (РПМ) – эффективный и надежный алгоритм множественного обмена для оптимального проектирования цифровых КИХ-фильтров с произвольными спецификациями. Данный алгоритм классический второй алгоритм Ремеза (Паркса – Макклеллана) с несколькими обменами. Для фильтрации, выбор КИХ-фильтров обычно обуславливается из-за их линейных фазовых характеристик. Свойства линейной фазы помогают сохранить важную информацию о времени дискретного сигнала, при этом приходится жертвовать низким значением порядка. Это увеличение порядка фильтрации влияет на вычислительную сложность и время отклика фильтра. Чтобы дополнительно проиллюстрировать компромисс между порядками фильтрации, вычислительным временем и временем отклика фильтра, были разработаны и реализованы фильтры различного порядка. Были разработаны фильтры РПМ типа 1 порядка m0 = 11, m2 = 199. Для всех конструкций КИХ полоса пропускания начинается с F0 = 48 Гц, а полоса пропускания начинается с F1 = 52 Гц, чтобы быть симметричной возле 50 Гц. Алгоритм Ремеза может проектировать линейно-фазовые фильтры четырех типов, для данной работы выбран тип I, как вариант по умолчанию для четного порядка. Библиотека scipy matplotlib в Python содержит функцию signal.freqz, которая вычисляет частотную характеристику цифрового фильтра.
Выбор порядка для фильтра: for length in [11, 15, 33, 67, 135, 199]:
b = signal.remez(length, (0, 0.18, 0.2, 0.50), (0.01, 1)), где length – порядок фильтра.
Создание этих сигналов с одинаковой длиной выборки называется нормализацией периода. Он может быть выполнен с помощью интерполяции или процесса децимации [8]. В контексте ЭКГ каждый удар сердца должен быть периодически нормализован, чтобы выполнить над ними любую математическую операцию.
Наиболее плоская геометрия и минимальная пульсация у фильтра с порядком 198(+1), при m1 = 67 затухание составляет Δ0,07, чего явно недостаточно для ослабления шума (рис. 3, а). Этот вывод дополнительно подтверждается в частотной области. Для ФР порядка m2 = 199 отмечается значительное улучшение результата. Во временной области сигнал, по-видимому, очищен от всех заметных шумов, за исключением некоторых довольно сильных колебаний, происходящих почти в течение первых двух секунд сигнала, т.е. присутствует «звон». В частотной области этого фильтра можно отметить, что шум значительно снизился ниже уровня других частот, присутствующих в отфильтрованном сигнале. График частотной области визуализирует этот процесс (рис. 3, б). Ослабление соседних частот (и даже в пределах частот среза) опять же относится к порядку фильтрации, очевидно, что порядок фильтрации влияет на «крутизну» полосы перехода (рис. 5, г).
а) б)
Рис. 3. а. Отношение между порядком фильтра и частотной характеристикой; б. График желаемых и фактических ЧХ
low = signal.remez (99,(0,0.03,0.04,0.50),(0.01,1)) и high (99,(0,0.1,0.12,0.50),(1,0.01))
На рис. 3, б, график желаемых и фактических частотных характеристик полосового фильтра РПМ 198-го порядка. Следующий код сначала использует функцию remez для проектирования фильтров высоких частот h1 и низких частот h2 соответственно, а затем свертку для расчета коэффициентов их каскадного фильтра h3.
Результаты исследования и их обсуждение
Конструкция надрезного фильтра БИХ с использованием метода размещения полюсов-нулей зависит от применяемой спецификации полосы пропускания. Узкая полоса пропускания привела к тому, что полюса, как правило, удаляются от центра единичного круга, и наоборот, затем узкая полоса пропускания режекторного фильтра обеспечивала идеальную фильтрацию только на частоте 50 Гц. Можно сравнить с результатом БПФ после фильтрации сигнала дал пульсации в диапазоне 30–70 Гц. Конструкция режекторного фильтра с использованием метода размещения полюсов-нулей от применяемой спецификации полосы пропускания (рис. 4).
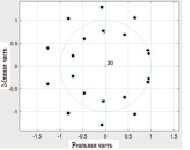
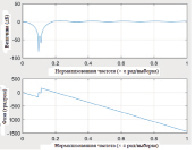
а) б)
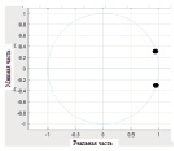
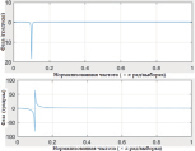
в) г)
Рис. 4. а. КИХ-фильтр, полюс/ноль; б. Частотная характеристика КИХ-фильтра; в. БИХ-фильтр, полюс/ноль; г. Частотная характеристика БИХ-фильтра
Из рис. 4 видно, что фильтр КИХ имеет более широкую и при этом глубокую выемку, чем фильтр БИХ. Это происходит из-за того, что фильтр КИХ имеет два нуля, близких к частоте выемки, вместо одного. Это делает фильтр более устойчивым к ошибкам в оценке частоты шума, но он также может ослаблять требуемые частотные компоненты. Кроме того, для конечного фильтра сложнее аппроксимировать постоянную характеристику из-за полиномиальной структуры вне выделенной частоты. Фильтр с конечной импульсной характеристикой является линейным фазовым фильтром, поскольку нули либо находятся на единичном круге, либо они отражаются на единичном круге. В нашей работе из-за ограничений линейной фазы порядок фильтрации составил 199 единиц. При этом БИХ-фильтры имеют более крутой переход от полосы пропускания к полосе затухания.
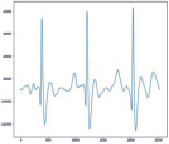
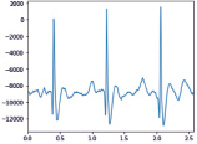
а) б)
Рис. 5. а. Результат фильтрации алг. Ремеза; б. Результат фильтрации алг. Чебышева 2
Оценки эффективности методов фильтрации для удаления ПЛП
|
Метод |
49,1 Гц |
50 Гц |
51,7 Гц |
|||
|
SNR |
RMSE |
SNR |
RMSE |
SNR |
RMSE |
|
|
КИХ Ремез |
42,20 ± 2,77 |
0,00 ± 0,00 |
20,37 ± 0,06 |
0,03 ± 0,01 |
1,15 ± 0,00 |
0,33 ± 0,13 |
|
БИХ Чебышев 2 |
34,71 ± 2,71 |
0,01 ± 0,01 |
15,22 ± 0,08 |
0,07 ± 0,03 |
1,00 ± 0,00 |
0,32 ± 0,11 |
|
БИХ Чебышев 1 |
33,40 ± 5,15 |
0,01 ± 0,01 |
37,37 ± 4,86 |
0,01 ± 0,00 |
6,57 ± 0,02 |
0,16 ± 0,06 |
Очевидно, что узкая полоса пропускания даёт фильтру лучший результат, чем широкая полоса (рис. 5). По значению RMSE видно, что чем уже полоса пропускания режекторного фильтра, тем меньше значение RMSE. Небольшое значение RMSE, показанное после фильтрации сигнала ЭКГ, было больше похоже на ЭКГ-сигнал без шума. В таблице показаны сводные данные с критерием качества для каждого метода фильтрации. Эффективность предложенных методов была количественно сопоставлена с другими методами на основе критериев качества. Производительность шумоподавления анализируется с использованием таких показателей, как отношение сигнал/шум, процентная среднеквадратичная разность, среднеквадратичная (среднеквадратичная) погрешность. SNR – это отношение мощности восстановленного сигнала к мощности шума (таблица). Было оценено три основных метода фильтрации шума ПЛП, в таблице результаты только для 49,1; 50 и 51,7 Гц. Данные в таблице показывают, что фильтры восстанавливают исходный уровень шумных сигналов. В результате выявлено, что лучшим методом фильтрации шума ПЛП по критерию качества с частотой 50,1 Гц является КИХ Ремеза с 0,0021 ± 0,0018 и 42,20 ± 2,77 соответственно, для RMSE и SNR. Статистическое тестирование подтвердило эти результаты со значимым значением p < 0,05. Для сравнения используются стандартные метрики.
Оба ПЗФ выдали хорошие характеристики в тех случаях, когда частота ПЛП правильно соответствует частоте среза цифровых фильтров (fc = 50 Гц). Однако при изменении частоты ПЛП производительность цифровых фильтров падает, поскольку они не могут адаптировать свою частоту среза к этому изменению. БИХ-фильтр Чебышева 2 показал довольно хороший отклик по всей величине по полосам пропускания, а полоса останова и переходные области имеют небольшую вычислительную мощность и, таким образом, подходят для одновременной обработки в реальном времени большого количества записей. Отклики на величину конструкции этого БИХ-фильтра были сопоставлены с алгоритмом КИХ Ремеза (Паркса – Макклеллана) в формате КИХ.
Порядок фильтра БИХ Чебышева 2 равен 4, а КИХ Ремеза – 199. Разработанные фильтры соответствуют общей спецификации. Очевидным сравнением является сравнение между фильтрами КИХ и БИХ. Было установлено, что фильтры БИХ обладают следующими преимуществами: они требуют значительно меньшего порядка для тех же спецификаций, то есть меньше вычислительная сложность, но на практике это преимущество не так заметно, если отношения порядков фильтров разных категорий не являются двузначными [9]. С другой стороны, фильтры КИХ обладают следующими свойствами: они всегда стабильны, могут быть спроектированы так, чтобы иметь линейную фазу, в случае оптимального фильтра можно управлять пульсацией полосы пропускания. Окончательный выбор между этими фильтрами зависит от типа приложения и бюджета. При ограниченном бюджете очевидным выбором был бы фильтр Чебышева 2 с минимальной сложностью. Если необходима линейная фаза, то выбор за фильтром Ремеза.
Заключение
Производительность фильтров анализируется путем сравнения мощности сигнала на частоте 50 Гц до и после фильтрации и искажения с формой волны ЭКГ. Установлено, что цифровые фильтры работают удовлетворительно. Режекторный фильтр Чебышева 2 четвертого порядка с шириной полосы пропускания 3 дБ, равной 0,2 (49,9–50,1), обеспечивает наилучшую производительность по сравнению с другими, поскольку он вносит минимальные искажения в форму волны ЭКГ. Фильтр БИХ Чебышева тип 2 – лучший компромисс между затуханием и фазовой характеристикой. Плоскость фильтра Чебышева достигается за счет относительно широкой области перехода от полосы пропускания к полосе заграждения со средними переходными характеристиками. В данной работе целью было создание режекторных фильтров, сделан вывод, что БИХ-режектор – лучший выбор фильтра, когда процесс удаления шумов проецируется на платформу ЦОС в реальном времени, так как рекурсивные фильтры дают лучшую производительность при уменьшении вычислительной мощности. Ввиду их минимальной вычислительной нагрузки эти фильтры должны найти применение в мониторах аритмии на базе микрокомпьютеров. Предложенный метод может эффективно устранять помехи линии электропередачи как на частоте 50 Гц, так и на частоте 60 Гц без ухудшения качества сигнала ЭКГ.
Библиографическая ссылка
Горяев В.М., Маштыков С.С., Бембитов Д.Б., Манджиева А.Н., Лиджиев Э.Б., Дорджиева Д.Е. АНАЛИЗ АППРОКСИМАЦИИ ЧЕБЫШЕВА ДЛЯ ФИЛЬТРОВ С КОНЕЧНЫМИ И БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ // Современные наукоемкие технологии. – 2021. – № 11-1. – С. 22-28;URL: https://top-technologies.ru/ru/article/view?id=38883 (дата обращения: 22.12.2024).