Судейство в танцевальном спорте характеризуется субъективной системой оценок, которая постоянно подвергается критике из-за низкой объективности. Судьи несут ответственность за быстрое и точное определение качества технических элементов и общего эстетического впечатления от выступления танцора на основе их личного восприятия выступления. Их задача усложняется еще и тем, что им нужно всего за полторы минуты оценить на танцполе шесть или двенадцать пар. До введения новой системы судейства в 2013 г. система судейства в танцевальном спорте не менялась в течение многих лет, в отличие от многих других эстетических видов спорта, таких как гимнастика [1], фигурное катание и др. [2], где изменения были внесены в течение последних десятилетий. Танцоры, тренеры и судьи критиковали старую систему судейства в танцевальном спорте, при этом основные их претензии заключались в том, что одни танцоры предпочитают других, что недостаточно времени для должной оценки каждого танцора и что танцоры не получают адекватных оценок качества их танца [3–5]. В связи с этим Всемирная федерация танцевального спорта разработала новую систему судейства, используя модель, аналогичную фигурному катанию, и представила ее в сентябре 2013 г. [6]. Теоретически цель этой новой системы состояла в том, чтобы обеспечить более объективное и надежное судейство и дать лучшую обратную связь для танцоров в отношении конкретных критериев их выступления. Основными отличиями новой системы являются определение четырех основных критериев судейства, большее количество судей и меньшее количество танцоров, танцующих одновременно. Танцоры исполняют на танцполе три сольных танца и два танца одновременно с шестью парами. В эстетических видах спорта имеется много аспектов, влияющих на объективность судейства [7–9]. Многочисленные исследования показали, что изменения в системе судейства в эстетических видах спорта в сторону абсолютизации оценок обычно приводят к более высокой объективности судейства [10–12]. Однако на сегодняшний день имеется лишь небольшое число исследований, посвященных судейству в танцевальном спорте, что, как следствие, вызывает опасения по поводу возможности систематической предвзятости и непоследовательности судейства в танцевальном спорте, которые могут повлиять на результаты соревнований. В связи с этим необходимо провести исследование качества судейства при использовании новой системы.
Хотя новая система судейства в танцевальном спорте и позиционируется как «Абсолютная судейская система» (AJS – Absolute Judging System), однако в соответствии с п. 13.1 ее правил «В предварительном раунде используется стандартная «система крестов». Председатель судейских коллегий опубликует список пар, которые перейдут в следующий раунд» [13]. При этом п. 8.2.1. говорит о том, что Чемпионаты мира WDSF, Открытые чемпионаты мира WDSF, Континентальные чемпионаты WDSF, Субконтинентальные чемпионаты WDSF, Мировые рейтинговые турниры WDSF, Кубки мира WDSF, Континентальные кубки WDSF и открытые соревнования должны включать как минимум первый раунд, полуфинал и финал, при этом в соответствии п. 8.1.2. для оценки первого раунда должна использоваться система «крестов» из системы «Скэйтинг» [14]. Таким образом, на предварительных этапах соревнований по новой судейской системе используется система «Скэйтинг», т.е. судья должен указать, какие спортсмены, по его / ее мнению, должны перейти в следующий раунд (т.е. на предварительных этапах используется система крестов). С другой стороны, имеется достаточное число работ, относящихся к разным видам спорта, свидетельствующих о том, что в международных соревнованиях одним из наиболее сильных факторов, влияющих на объективность оценки судей, являются их национальные предпочтения [2].
Чемпионат мира состоит из трех различных дисциплин: стандартных танцев (вальс, танго, венский вальс, медленный фокстрот и квикстеп), латиноамериканских танцев (самба, ча-ча-ча, румба, пасодобль и джайв) и десяти танцев (пяти стандартных танцев и пяти латиноамериканских танцев).
Следовательно, целью данной части работы является анализ национальных предпочтений судей на международных соревнованиях по танцевальному спорту. Для этого были проанализированы опубликованные в интернете результаты Чемпионата мира 2019 г. (WDSF World Championship), проходившем в Москве (Россия) 07 Сентября 2019 г. (10 танцев, Латина) и в Вильнюсе (Литва) 30 Ноября 2019 г. (Стандарт).
Материалы и методы исследования
В данной статье проанализированной дисциплиной являются латиноамериканские танцы. Исходные данные для анализа взяты с сайта WDSF (WDSF World Championship taken place in Moscow – Russia on 07 September 2019) (рис. 1).

Рис. 1. Исходные данные для анализа с сайта WDSF
В данном соревновании система крестов применялась, так же как и в стандарте, в 1–2 раундах и перетанцовке 1 раунда.
Далее данные переносились в программу MS Excel (рис. 2, А), зашифрованные обозначения национальности арбитров и стран расшифровывались (рис. 2, Б) и пары из одних стран с арбитрами маркировались. Потом данные по каждому арбитру и парам из одной с ним страны переносились на отдельный лист, группировались для каждой пары и для каждой пары рассчитывалось среднее число баллов, данное ей судьей из одной с ней страны, и среднее число баллов, данное ей всеми остальными судьями (рис. 3).

А
Рис. 2. Общий вид перенесенных в программу MS Excel исходных данных (А) и результаты их расшифровки и обработки (Б) (начало рисунка)
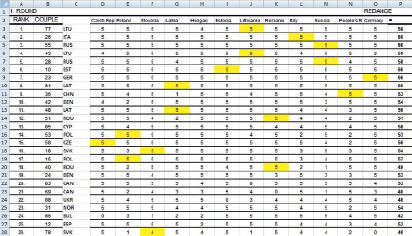
Б
Рис. 2. Общий вид перенесенных в программу MS Excel исходных данных (А) и результаты их расшифровки и обработки (Б) (окончание рисунка)

Рис. 3. Обработка данных по каждому арбитру и парам из одной с ним страны
Поскольку у всех арбитров на данном соревновании присутствовали «свои» спортсмены, т.е. среди арбитров из Нидерландов, Беларуси, Китая, США, Франции, Латвии, Германии, России, Литвы, Италии, ЮАР и Испании судей без «своих» спортсменов не было обнаружено – у каждого из судей на паркете на данном этапе соревнований присутствовали по две пары из одной с ним страны, то вместо контрольной группы судей «без своих» спортсменов были случайным образом выбраны судьи из двух стран (ЮАР и Литвы), для которых данный коэффициент рассчитывался как отношение числа крестов, выставленных этими судьями тем же группам спортсменов.
Вариационный анализ рядов и расчет t-критерия Стьюдента [15] проводился при помощи онлайн-калькулятора медицинской статистики https://medstatistic.ru.
Результаты исследования и их обсуждение
Таким образом, прежде всего, был проведен анализ средних оценок, выставленных судьями парам из одной с ними страны, и его сравнение с оценками, выставленными этим парам другими судьями (таблица).
Средние оценки, выставленные судьями парам из одной с ними страны, средняя оценка, выставленная судьей из Литвы, судьей из Южной Африки (ЮАР), и средние оценки, выставленные этим парам другими судьями, и разница между ними. Чемпионат мира, латиноамериканские танцы
|
Страна |
Средняя оценка, выставленная судьей из одной с парой страны (1) |
Средняя оценка, выставленная судьей из Литвы (2) |
Средняя оценка, выставленная судьей из Южной Африки (ЮАР) (3) |
Средняя оценка, выставленная остальными судьями (4) |
|
Нидерланды |
0,5 |
0 |
0,0 |
0 |
|
0 |
0,5 |
0,0 |
0 |
|
|
Беларусь |
2,5 |
0 |
0,0 |
1,1 |
|
Китай |
5 |
2,3 |
5,0 |
4,5 |
|
5 |
3,7 |
4,7 |
4,1 |
|
|
США |
4,3 |
0 |
3,0 |
1,3 |
|
5 |
1,5 |
1,0 |
1,6 |
|
|
Франция |
5 |
5 |
5,0 |
5 |
|
5 |
2,3 |
3,3 |
2,8 |
|
|
Латвия |
5 |
4,3 |
4,3 |
3,9 |
|
5 |
3,7 |
2,3 |
3,8 |
|
|
Германия |
5 |
5 |
4,7 |
5 |
|
5 |
5 |
5,0 |
5 |
|
|
Россия |
5 |
5 |
5,0 |
5 |
|
5 |
5 |
5,0 |
5 |
|
|
Литва |
5 |
5 |
2,7 |
2,5 |
|
4,7 |
4,7 |
2,7 |
1,5 |
|
|
Италия |
5 |
4,7 |
4,7 |
4,6 |
|
5 |
3,7 |
5,0 |
4,7 |
|
|
ЮАР |
0 |
0,5 |
0,0 |
0,2 |
|
0 |
0 |
0,0 |
0 |
|
|
Испания |
5 |
2,3 |
5,0 |
3,8 |
|
5 |
3,3 |
4,3 |
3,3 |
|
|
Окончание таблицы |
||||
|
Страна |
Средняя оценка, выставленная судьей из одной с парой страны (1) |
Средняя оценка, выставленная судьей из Литвы (2) |
Средняя оценка, выставленная судьей из Южной Африки (ЮАР) (3) |
Средняя оценка, выставленная остальными судьями (4) |
|
Средняя арифметическая (М) |
4,00 |
2,93 |
3,16 |
2,99 |
|
Медиана (Ме) |
5 |
3,7 |
4,3 |
3,8 |
|
Стандартное квадратичное отклонение (σ) |
1,90 |
1,97 |
2,01 |
1,87 |
|
Коэффициент вариации (Cv) |
47,40 % |
67,04 % |
63,71 % |
62,60 % |
|
Средняя ошибка средней арифметической (m) |
0,40 |
0,42 |
0,43 |
0,40 |
Поскольку соревнования судили арбитры из Нидерландов, Беларуси, Китая, США, Франции, Латвии, Германии, России, Литвы, Италии, ЮАР и Испании, то для каждой пары из этих стран (а в соответствии с правилами соревнований в них участвовало максимум по две пары из каждой страны), как описано выше, рассчитывалось среднее значение баллов, данных ей конкретным судьей, и среднее значение баллов, данных паре остальной группой судей.
Поскольку у всех арбитров на данном соревновании присутствовали «свои» спортсмены, т.е. среди арбитров из Нидерландов, Беларуси, Китая, США, Франции, Латвии, Германии, России, Литвы, Италии, ЮАР и Испании судей без «своих» спортсменов на танцполе также не было обнаружено – у каждого из судей на паркете на первом туре соревнований присутствовали пары из одной с ним страны – то также вместо контрольной группы судей «без своих» спортсменов были случайным образом выбраны судьи из двух стран (Южной Африки (ЮАР) и Литвы), для которых данный коэффициент рассчитывался как отношение числа крестов, выставленных этими судьями тем же группам спортсменов. Таким образом, аналогично предыдущему разделу, был проведен анализ средних оценок, выставленных судьями парам из одной с ними страны, и его сравнение с оценками, выставленными этим парам другими судьями (таблица).
Как видно из таблицы, при попарном сравнении столбцов данных 1 и 4 ясно, что средние оценки, выставленные судьями парам из одной с ними страны, практически всегда или совпадают, или выше, чем средние оценки, выставленные этим парам другими судьями.
Однако сравнение этих рядов показывает, что различия между ними статистически не значимы (p = 0,081244) при уровне значимости α = 0,05.
Интересно отметить, что, при исключении из данного списка судей из Нидерландов и ЮАР, для средних оценок, выставленных судьями парам из одной с ними страны (столбца 1) при числе единиц наблюдения, равном 19, средняя арифметическая (М) становится равна 4,82, медиана (Ме) = 5, стандартное квадратичное отклонение (σ) = 0,59, коэффициент вариации (Cv) = 12,17 %, а средняя ошибка средней арифметической (m) = 0,14. При этом для средних оценок, выставленных остальными судьями, при числе единиц наблюдения (n) = 19, средняя арифметическая (М) становится равна 3,61, медиана (Ме) = 3,9, стандартное квадратичное отклонение (σ) = 1,40, коэффициент вариации (Cv) = 38,75 %, а средняя ошибка средней арифметической (m) = 0,33.
Сравнение этих рядов показывает, что значение t-критерия Стьюдента = 3,38 и, следовательно, различия между ними уже статистически значимы (p = 0,001816) при уровне значимости α = 0,05, поскольку при числе степеней свободы f = 36 критическое значение t-критерия Стьюдента = 2,028.
Таким образом, 10 из 12 судей, судивших это соревнование, в отношении своих соотечественников судили его предвзято.
Графически эти результаты представлены на рис. 4, А и В, на которых хорошо видно, что практически все оценки, выставленные судьями парам из одной с ними страны, выше, чем средняя оценка, данная этим парам другими судьями – абсолютное большинство точек лежит ниже красной линии, которая представляет собой линию, на которой находились бы точки при равных оценках, выставленных анализируемой группой судей (имеющих на танцполе спортсменов из своей страны) и остальными судьями. Более того, видно, что значительному числу спортсменов из своей страны судьи ставили высшие оценки, невзирая на оценки других судей.
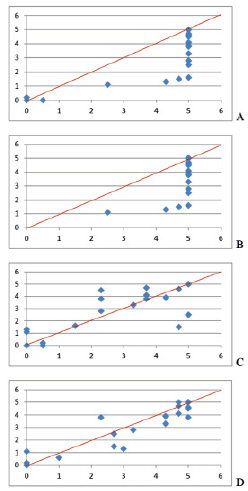
Рис. 4. Отношение оценок, выставленных судьями парам из одной с ними страны (по оси Х), и оценок, выставленных этим парам другими судьями (по оси Y) (A), отношение этих же оценок без учета оценок арбитров из Нидерландов и ЮАР (B), отношение оценок, выставленных судьей из Литвы (С) и Южной Африки (ЮАР) (D) этим же парам, (по оси Х), и оценок, выставленных этим парам другими судьями
Поскольку у всех арбитров на данном соревновании присутствовали «свои» спортсмены, вместо контрольной группы судей «без своих» спортсменов были случайным образом выбраны судьи из двух стран Литвы и ЮАР (Южной Африки). Далее рассмотрим оценки этих двух судей.
Прежде всего, анализ показывает, что оценки, выставленные этими судьями спортсменам, статистически не отличаются от оценок, выставленных им всем пулом судей. Для судьи из Литвы это отличие составляло p = 0,918088, а для судьи из Южной Африки p = 0,773614 при уровне значимости α = 0,05.
Далее был проведен анализ средних оценок, выставленных судьей из Литвы парам, проанализированным ранее, и их сравнение с оценками, выставленными этим парам судьями из одной с парами страны (таблица). Это сравнение показывает, что различия между ними статистически не значимы (p = 0,071958) при уровне значимости α = 0,05. Однако если при анализе «своих пар» не учитывать оценки, выставленные «своим» парам судьями из Нидерландов и ЮАР, то различия становятся статистически достоверными (p = 0,000121).
Аналогичный анализ, проведенный для средних оценок, выставленных судьей из Южной Африки парам, проанализированным ранее, показывает, что различия между ними также статистически не значимы (p = 0,144859) при уровне значимости α = 0,05. При этом при аналогичном исключении из анализа оценок выставленных «своим» парам судьями из Нидерландов и ЮАР, различия также становятся статистически достоверными (p = 0,000723).
Интересно также отметить, что коэффициенты вариации оценок, выставленных анализируемым спортсменам всеми судьями (62,60 %), а также судьями и Литвы (67,04 %) и ЮАР (63,71 %), очень близки между собой. При этом коэффициент вариации оценок, выставленных анализируемым спортсменам «своими» судьями, уже значительно меньше (47,40 %), а при исключении из этого анализа оценок, выставленных «своим» парам судьями из Нидерландов и ЮАР, он падает до 12,17 %, что говорит о близости оценок, выставляемых «своим парам» большинством судей на этих соревнованиях.
Графически эти результаты представлены на рис. 4, С и D, на которых видно, что, в отличие от рис. 4, А и В, точки равномерно распределены как выше, так и ниже линии равенства оценок, данных конкретной паре судьей, средним оценкам этой пары, данным ей всеми судьями.
Следовательно, мы видим, что в целом оценки, выставленные парам судьями из одних со спортсменами стран, не отличаются статистически достоверно от оценок, выставленных этим парам судьями из Литвы и Южной Африки (ЮАР). Однако если при этом в пуле оценок, выставленных «своим» парам, не учитывать оценки, выставленные судьями из Нидерландов и ЮАР, то тогда эти различия уже статистически достоверны.
Заключение
Национальные предпочтения в эстетическом спорте давно привлекают внимание исследователей [1]. Именно эти национальные предпочтения судей вызвали изменения в системе судейства в фигурном катании [10], за которыми последовало введение новой «абсолютной» системы судейства и в танцевальных видах спорта [3]. Однако, по-видимому, национальные предпочтения судей играют важную роль и в настоящее время.
Наш анализ показал, что коэффициент вариации (Cv) оценки судьи для спортсмена из его страны на танцполе в целом = 47 % (а для большинства – 10 из 12 судей – даже 12 %), против 62–67 % во всех остальных случаях из-за переоценки судьями спортсменов из той же страны. В то же время, несмотря на то, что в других случаях судьи ставили некоторым спортсменам наивысшие баллы, которые были выше, чем средние баллы, полученные этими спортсменами, в целом разброс оценок, даваемых судьями спортсменам из других стран, был больше. Аналогичные результаты о различиях в оценке были также получены Premelč с соавторами [2], которые при анализе финала конкурса обнаружили, что относительно большие различия между оценками судей указывают, по их мнению, на различия в том, как судьи воспринимали качество танцоров или их интерпретацию судейской шкалы. Эти результаты были получены в финале конкурса с использованием абсолютной системы судейства. Однако объективность судейства играет важную роль не только в финале соревнований, для танцоров, занявших первое место, но и для других спортсменов, выбывших из соревнований в первых раундах, когда в рамках абсолютной системы используется система крестов.
Таким образом, результаты судейства двух случайно выбранных арбитров, да и всех проанализированных двенадцати арбитров в целом, применительно к анализируемой группе спортсменов статистически значимо не отличаются от результатов судейства в целом. Однако в то же время судейство спортсменов из одной страны большинством судей (10 из 12) статистически значимо отличается от судейства спортсменов из других стран.
Библиографическая ссылка
Сингина Н.Ф. НАЦИОНАЛЬНЫЕ ПРЕДПОЧТЕНИЯ СУДЕЙ В ПЕРВЫХ ТУРАХ ТАНЦЕВАЛЬНОЙ ДИСЦИПЛИНЫ «ЛАТИНОАМЕРИКАНСКИЕ ТАНЦЫ» ЧЕМПИОНАТА МИРА WORLD DANCESPORT FEDERATION // Современные наукоемкие технологии. 2021. № 10. С. 190-197;URL: https://top-technologies.ru/ru/article/view?id=38876 (дата обращения: 06.02.2026).
DOI: https://doi.org/10.17513/snt.38876



