На современном этапе образовательный процесс в педагогических вузах реализуется в условиях двухуровневой системы – бакалавриата и магистратуры – на основании положений и требований федерального государственного образовательного стандарта высшего образования (ФГОС ВО), который соответствует данному уровню подготовки. Обучение по программе бакалавриата осуществляет базовую фундаментальную подготовку, а по программе магистратуры ведется специализированная и углубленная подготовка студентов. Магистратура понимается как второй уровень высшего образования.
Основным подходом к организации учебного процесса в стандартах бакалавриата и магистратуры обозначен компетентностный подход. Он ориентирует на формирование универсальных, общепрофессиональных и профессиональных компетенций у обучающихся, а также на самоопределение и развитие индивидуальности каждого студента. В соответствии с данным подходом цели математического образования в педвузе предполагают формирование компетентной личности, способной к профессионально-педагогической деятельности в условиях информационного общества.
«В современном обществе всё большее значение приобретает способность комплексного решения разного рода проблем с применением углубленных фундаментальных и прикладных знаний, получаемых по различным направлениям. Этим требованиям сегодня в большей степени соответствуют выпускники магистратуры» [1, с. 75]. Цель обучения в магистратуре по различным направлениям подготовки – подготовка кадров более высокой квалификации по сравнению с бакалавриатом, которая предусматривает углубленное освоение профильных дисциплин, прохождение производственной практики, самостоятельное выполнение исследовательских проектов.
В Мордовском государственном педагогическом университете разработана магистерская программа по направлению «Педагогическое образование», профиль «Математическое образование». Цель этой программы – подготовить выпускников, которые способны, опираясь на сформированные в процессе обучения компетенции, качественно и самостоятельно решать задачи профессиональной деятельности в области математического образования. В программе определены три типа задач профессиональной деятельности: педагогический, проектный и научно-исследовательский – выделены соответствующие им компетенции и индикаторы их достижения. В качестве основной педагогической задачи поставлена задача реализации образовательных программ разного уровня (базового и углубленного) по математике на ступени среднего общего образования. Следующие два типа задач (проектный и научно-исследовательский) ориентированы на проектирование содержания таких программ и их учебно-методического обеспечения, а также на анализ системы математического образования и создания механизмов и инструментария для её совершенствования.
Для достижения цели и задач, сформулированных в магистерской программе, необходим высокий уровень математической компетентности будущего педагога.
Цель исследования – раскрыть содержание понятия «математическая компетентность будущего учителя математики» и разработать приемы её формирования у студентов педагогического вуза в условиях магистратуры.
Материалы и методы исследования
В ходе исследования использовались материалы ФГОС ВО по направлению подготовки «Педагогическое образование», а также содержание математических и методических дисциплин, изучаемых в педагогическом вузе на уровнях бакалавриата и магистратуры. Для получения результатов применялись следующие методы: наблюдение за процессом усвоения математических знаний; беседа с обучающимися и преподавателями; педагогический эксперимент; анализ и обобщение собственного опыта обучения студентов магистратуры математическим дисциплинам.
Результаты исследования и их обсуждение
Использованию компетентностного подхода в математическом образовании посвящены работы таких авторов, как Р.А. Абдусаламов, Н.А. Бушмелева, Г.И. Саранцев, Е.А. Сетько, В.А. Тестов и др. Однако в научной литературе формированию математической компетентности студентов магистратуры педагогического направления, на наш взгляд, уделяется недостаточно внимания. Не выделены четко компетенции, составляющие математическую компетентность будущего педагога-магистра, не указаны приемы их формирования. Остановимся на этом подробнее.
Понятие «компетенция/компетентность» трактуется по-разному, наиболее распространенной является трактовка, согласно которой содержание компетенции составляют знания, умения и способы действий. Компетенция, для того чтобы стать компетентностью конкретной личности, должна пройти через деятельность. Компетентность, как отмечает В.Н. Янушевский, это знание в действии [2, с. 5]. Исходя из определения математики как науки, математическая компетентность – это способность структурировать данные, выделять математические отношения, строить математическую модель ситуации, анализировать и преобразовывать её, интерпретировать полученные результаты [3]. Иначе говоря, математическая компетентность предполагает владение математическими методами и адекватное их применение при решении проблем, возникающих в профессиональной сфере и в повседневной жизни.
Учитывая вышесказанное, можно выделить следующие компетенции, составляющие математическую компетентность будущего учителя математики, формируемую у студентов педагогического направления в условиях магистратуры:
– способность представлять структуру основных математических методов и применять их для решения задач повышенного уровня сложности;
– способность интегрировать математические знания и применять интеграцию алгебраического и геометрического методов в решении задач разного уровня сложности;
– способность осуществлять математическое моделирование ситуации, представленной в задаче, с соблюдением этапов моделирования и различать «мягкие» и «жесткие» модели;
– способность обосновывать основные понятия и утверждения элементарной математики с точки зрения высшей математики;
– способность использовать информационные технологии в решении математических задач повышенного уровня сложности и задач профессиональной деятельности.
Для формирования вышеуказанных компетенций следует использовать современные деятельностные технологии, инновационные активные методы преподавания и умело сочетать дистанционные и недистанционные формы организации самостоятельной работы студентов. Основным видом самостоятельной работы по математике является решение задач, поэтому большое значение имеет формирование умений выполнять анализ условия задачи, осуществлять поиск решения путем выявления закономерностей и установления связей между данными и искомыми. Некоторые примеры организации такой работы приведены в статье [4].
Формирование математической компетентности студентов проходит два этапа. Первый этап реализуется в условиях бакалавриата, где они знакомятся с методами фундаментальных математических дисциплин (геометрии, алгебры и теории чисел, математического анализа, теории вероятностей и математической статистики), овладевают действиями, составляющими данные методы. Однако на этом этапе, как показывает практика, знания, полученные в процессе обучения, ещё не переходят в методы. Большинство студентов не могут применять их при решении текстовых и прикладных задач. Одной из причин этого является сокращение количества часов, отводимых на изучение математических дисциплин в условиях бакалавриата, что не позволяет студентам на должном уровне овладеть методами этих дисциплин. Усвоение какого-либо метода предполагает овладение не только действиями, составляющими данный метод, но и его теоретическим базисом (системой знаний). Без системы знаний метод не существует, не сразу система становится методом. «Метод – это такая система знаний, которая уже используется или для дальнейшего познания, или для преобразования объекта. Знание в процессе обучения переходит в метод» [5, с. 155].
Таким образом, на втором этапе, который соответствует уровню магистратуры, должны происходить систематизация и обобщение базовых математических знаний студентов, полученных в условиях бакалавриата, преобразование их в методы и применение к решению задач. Здесь магистранты должны получить все необходимые знания об изучаемых методах и особенностях их применения в разных ситуациях.
Остановимся кратко на содержании понятия «метод». В теории научного познания и методике обучения математике (Е.И. Лященко, Т.Ф. Кириченко, Г.И. Саранцев и др.) установлено, что знания о методе включают в себя знания о его компонентах (гносеологических и деятельностных) [6]. К гносеологическим компонентам метода относится система знаний, на которой он основан и которая позволяет применять его в разных ситуациях.
Для того чтобы овладеть каким-либо методом задач, надо знать:
1) характер задачи (ее тип, вид) и ее теоретический базис (основные понятия и утверждения, свойства понятий, связи между ними);
2) следствия, полученные в ходе анализа условия задачи и выделения в нем существенных компонентов, результаты выявления закономерностей, установления связей между данными и искомыми;
3) круг задач, решаемых данным методом, и особенности его использования в разных случаях (при разных условиях, в разных системах координат и т.д.).
Деятельностные компоненты метода – это система действий, выполнение которых ведет к решению задачи и получению ответа.
Усвоение магистрантами, будущими учителями, методов математики и понимание методических особенностей этого усвоения имеет большое общеобразовательное и мировоззренческое значение, так как обучение методам направлено на обобщение и систематизацию полученных знаний. Знания, усвоенные в процессе обучения, в результате осмысления через призму метода открывают перед обучающимися другие свои сущностные стороны, что способствует их углублению, включению в новые связи, отношения. Наряду с этим изучение методов, установление их гносеологических и деятельностных компонентов дает возможность студентам лучше понять приемы решения отдельных типов задач.
Методы математики выполняют также интегрирующую функцию, которая влияет на формирование определенного мировоззрения обучающихся. Во-первых, через приложения методов можно увидеть связь математики с другими науками, с практикой; во-вторых, выделить общие признаки всех методов математики и условий их применения.
В методологическом отношении изучение методов математики дает возможность раскрыть перед студентами содержание понятия «метод» и выделить его компоненты. Поэтому в ходе изучения конкретного метода целесообразно представлять его структуру в виде схемы, отражающей его гносеологические и деятельностные компоненты. Задания на составление такой схемы могут быть предложены и для самостоятельной работы студентов. Например, методы вычисления площадей фигур с помощью определенного интеграла в декартовых координатах представлены на рис. 1.
Рис. 1. Структурная схема методов вычисления площадей фигур с помощью определенного интеграла
Выделены пять методов: метод непосредственного применения формулы для вычисления площади криволинейной трапеции; метод, использующий свойство аддитивности площади; метод, основанный на разности площадей двух криволинейных трапеций; метод вычисления площади фигуры, в случае, когда функция принимает неположительные значения; комбинированный метод. Рассмотрены разные случаи применения названных методов и определены составляющие их действия. В ходе исследования приведены конкретные примеры, иллюстрирующие каждый метод.
Следует заметить, что аналогично слу- чаю декартовых координат была рассмотрена структура методов вычисления площадей фигур при параметрическом задании кривой и в полярных координатах.
Структура метода исследования функции на выпуклость и точки перегиба, изучаемого в курсе математического анализа, представлена на рис. 2.
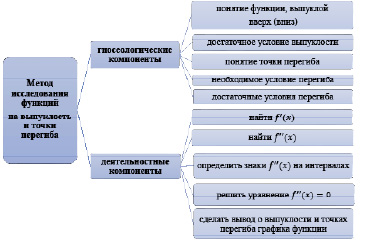
Рис. 2. Структура метода исследования функции на выпуклость и точки перегиба
Формирование математической компетентности магистрантов предполагает также формирование их компетентности в области интеграции математических знаний (методов). Как известно, использование компетентностного подхода в учебном процессе ориентировано на разработку интегрированных учебных дисциплин (математических и методических, математических и дисциплин, относящихся к компьютерным наукам и т.д.), в которых основные профессиональные понятия объединяют (интегрируют) знания учащихся из разных дисциплин, придают им практическую, реальную значимость [7].
В МГПУ имени М.Е. Евсевьева в учеб- ный план магистратуры профиля «Математическое образование» введена специальная дисциплина «Интеграция алгебраического и геометрического методов в среднем математическом образовании», на занятиях которой студенты не только знакомятся с понятием интеграции алгебраического и геометрического методов, но и учатся применять геометрический метод в решении алгебраических текстовых задач и алгебраические методы (метод уравнений и неравенств, координатный, векторный) в решении геометрических задач.
Интеграция алгебраического и геометрического методов – это процесс сочетания или связи (слияния) данных методов, осуществляемый обучающимся путем перевода учебной информации с алгебраического языка на геометрический или с геометрического языка на алгебраический и обратно. Механизм интеграции состоит из трех возможных ситуаций.
Ситуация 1. Дана алгебраическая задача. Решение осуществляется по этапам.
1 этап. Перевод алгебраической задачи на геометрический язык.
2 этап. Решение полученной задачи на геометрическом языке.
3 этап. Перевод полученного ответа на алгебраический язык (иногда этот этап отсутствует или осуществляется автоматически).
П р и м е р 1. Решить неравенство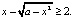 
1 этап. 1) Запишем неравенство в виде: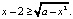 
2) Переведем задачу на графический язык. Представим в виде функций левую и правую части неравенства: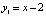 
, 
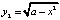и построим графики этих функций в одной системе координат (рис. 3).
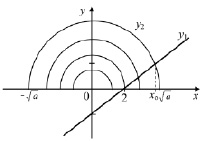
Рис. 3. Геометрическая модель к примеру 1
Получим прямую линию и полуокружность (расположенную в верхней полуплоскости) с центром в точке x = 0 и радиусом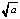 
. График полуокружности строится при различных значениях параметра а.
2 этап. Из рисунка видно, что графики функций y1 и y2 имеют общую точку, т.е. уравнение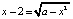 
имеет единственный корень xо, если а ≥ 4.
При а = 4, то существует единственный корень xо = 2.
При а > 4, единственный корень уравнения принадлежит интервалу (4;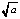 
).
На геометрическом языке решить данное неравенство значит указать промежуток значений х, при которых график функции y1 лежит не ниже графика функции y2.
Из рис. 3 ясно, что xо ≤ x ≤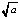 
. Решение уравнения x – 
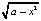= 2 дает два корня: 
; 
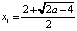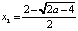. Корень x2 не входит в интервал (2; 
).
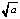3 этап. Отрезок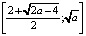 
является решением исходного неравенства.
Ситуация 2. Дана геометрическая задача. Этапы ее решения следующие.
1 этап. Перевод геометрической задачи на алгебраический язык (координатный, векторный, уравнений и неравенств).
2 этап. Решение полученной задачи на алгебраическом языке.
3 этап. Перевод полученного ответа на геометрический язык.
П р и м е р 2. Дан треугольник KMN, биссектриса MP и медиана KL которого образуют прямой угол, MP = KL = 4. Найти стороны треугольника KMN.
Замечание. Если O – точка пересечения отрезков MP и KL, то треугольники KMO и LMO равны (рис. 4). Поэтому KО = ОL = 2 и KM = ML, так что MN = 2KM.
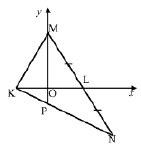
Рис. 4. Модель к примеру 2
1 этап. Введем прямоугольную систему координат c началом в точке O и единицей масштаба –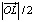 
. Тогда получим: K(–2; 0), L(2; 0) и пусть M(0; a).
Так как L – середина отрезка MN, то N(4; –a). Точка P имеет координаты (0: y). Так как P принадлежит прямой KN, то составим уравнение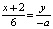 
. Откуда y = – 
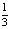a. Тогда MP = 
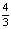a. Так как MP = 4, то a = 3.
В результате получим: K(–2; 0), M(0; 3), N(4; –3).
2 этап. Используя формулу расстояния между двумя точками, которые заданы своими координатами, находим длины сторон треугольника АВС.
3 этап.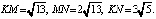 
Ситуация 3. Дана интегрированная задача. Решение выглядит следующим образом.
1 этап. Одна часть задачи переводится на алгебраический язык.
2 этап. Решение первой части задачи на алгебраическом языке.
3 этап. Вторая часть задачи переводится на геометрический язык.
4 этап. Решение второй части задачи на геометрическом языке.
5 этап. Перевод полученного ответа на язык исходной задачи.
Разбор всех этих ситуаций со студентами следует сопровождать решением соответствующих задач и дальнейшим их обсуждением. Результатом такого обсуждения должно быть понимание того, что алгебраический и геометрический методы решения задач являются конкретизацией метода математического моделирования. Поэтому в процессе решения всех задач со студентами необходимо четко выделять три этапа моделирования: формализацию (перевод задачи на математический язык), решение задачи на алгебраическом или геометрическом языке; перевод полученного решения на язык задачи.
При формировании компетентности в области интеграции математических методов и моделирования необходимо предусматривать знакомство студентов с современной трактовкой предмета математики. Как показало наше исследование, большинство студентов не могут ответить на вопрос «Что такое математика?». Классическое определение математики дал Ф. Энгельс в своей работе «Анти-Дюринг» (1877 г.): «Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира, стало быть, весьма реальный материал». Спустя 100 лет Л.Д. Кудрявцев определяет математику как область человеческого знания, в которой изучаются математические модели [8, с. 30]. В.И. Арнольд в своей работе [9] (1997 г.) выделяет при этом еще «жесткие» и «мягкие» модели. Жесткие модели – это готовые рецепты решения задач, мягкое моделирование предполагает математический подход к явлениям реального мира. Учитывая схожесть моделей, основанных на одной и той же схеме и применяемых в разных научных областях, М.М. Постников делает вывод о том, что математикой называется наука о схемах моделей окружающего мира. Она изучает «все возможные – хотя бы мысленно – схемы, их взаимосвязи, методы их конструирования, иерархии схем (схемы схем) и т.д.» [10, с. 85]. Тем самым было подчеркнуто усиление абстрактного характера математики, однако это не отрывает её от реальной действительности, а ещё больше сближает с ней через многочисленные приложения в разных областях.
Большое значение в формировании математической компетентности студентов имеет интеграция математики и информатики. Математическое моделирование и использование компьютерной техники для проведения эксперимента позволяют расширить и интегрировать знания различных дисциплин, усилить прикладную и практическую направленность обучения как в области математики, так и в области информатики. Кроме этого, интегрированный подход дает возможность активизировать творческую деятельность студентов, формировать навыки систематического использования компьютерной техники.
К математической компетентности будущего учителя математики следует отнести и его компетентность в области развития математических способностей школьников. В этом плане необходимо знать структуру математических способностей, их основные компоненты (геометрический, логический, алгоритмический, оперирование абстракциями) и пути их развития у учащихся. Более подробно этот материал изложен в статье [11].
Заключение
Компетентность следует понимать как владение определёнными компетенциями, каждую из которых составляют знания, умения и способы действия. Усложнение задач, решаемых в обществе, в том числе и в образовании, требует сегодня подготовки высококвалифицированных кадров, способных находить оригинальное, нестандартное решение проблем, возникающих в профессиональной деятельности. Этим требованиям должны соответствовать выпускники магистратуры. В области высшего педагогического образования в настоящее время актуальной задачей является определение состава и путей формирования математической компетентности, которая позволила бы выпускникам на современном уровне качественно и эффективно выполнять свою педагогическую деятельность.
Математическая компетентность студентов магистратуры должна формироваться, во-первых, с учетом структуры и логики математической науки в целом и углубленного изучения отдельных её дисциплин и, во-вторых, с учетом профессионального поля деятельности – образования. Учитывая это, в процессе обучения магистрантов необходимо формировать компетентность: 1) в области структуры математических методов и их применения к решению задач; 2) в области интеграции алгебраического и геометрического методов решения задач, а также предмета математики и математического моделирования; 3) в области интеграции математики и информатики, применения компьютерных технологий в решении математических задач; 5) в области структуры и путей развития математических способностей школьников.
Итак, компетентностный подход к организации учебного процесса студентов является необходимым условием обеспечения непрерывности и качества математического образования в педагогическом вузе.
Исследование выполнено в рамках гранта на проведение научно-исследовательских работ по приоритетным направлениям научной деятельности вузов-партнеров по сетевому взаимодействию (Южно-Уральский государственный гуманитарно-педагогический университет и Мордовский государственный педагогический университет имени М.Е. Евсевьева) по теме «Формирование математической компетентности студентов педагогического вуза в условиях магистратуры».
Библиографическая ссылка
Капкаева Л.С. ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНТНОСТИ СТУДЕНТОВ ПЕДАГОГИЧЕСКОГО ВУЗА В УСЛОВИЯХ МАГИСТРАТУРЫ // Современные наукоемкие технологии. – 2021. – № 10. – С. 135-142;URL: https://top-technologies.ru/ru/article/view?id=38867 (дата обращения: 21.11.2024).